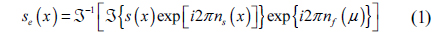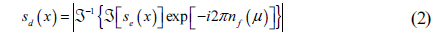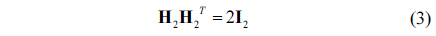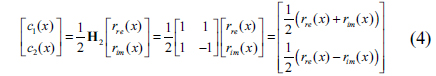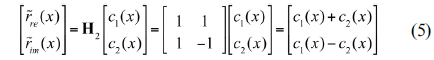In data transmission, encryption techniques are necessarily required in order to prevent unauthorized access. Thus, encryption techniques have been widely studied [1-18].In particular, optical encryption techniques with an advantage in terms of the encryption speed have been well researched [5-16]. Double random phase encryption (DRPE), which is the most widely used optical encryption technique, has been proposed [5]. It can be implemented easily and its speed of encryption is faster than that of non-optical encryption methods. DRPE employs two independent random phase masks to encrypt the primary image. Although such an optical encryption technique improves the security of the transmission information, color information cannot be handled in decryption since the primary image is illuminated with monochromatic light [19].
DRPE-based encryption techniques for a color image have been presented [19, 20]. The color image encryption using fractional Fourier transforms [19] and the color image encryption by wavelength multiplexing based on lensless Fresnel transform holograms [20] have been proposed. In these techniques, the color image is separated into red, green, and blue components, and they are independently encrypted. Also, these techniques use many keys for both encryption and decryption. Though the data security can improve with an increase in the number of keys or the length of keys, the encryption and decryption system can become more complicated as the amount of key information rises.
In this paper, we propose a simple DRPE-based orthogonal encoding technique for color image encryption. In the proposed technique, a color image is segregated into red, green, and blue components before encryption and each of the components is independently encrypted, analogous to the previous encryption techniques. However, we employ DRPE using the same key in encrypting three components in order to reduce the complexity of encryption and decryption, unlike the previous cases. In addition, we adopt a Hadamard matrix [21] with orthogonal property in order to encode the encrypted data in each of red, green, and blue channels. The orthogonal encoding scheme is able to enhance the security of DRPE using the same key for three components at the expense of a little complexity. Furthermore, the orthogonal encoder is easy to implement because it consists of simple linear operations. Therefore, the proposed DRPE-based orthogonal encoding technique can be a low-complexity and effective encryption technique for color images.
The paper is organized as follows. First we briefly present the DRPE in Section II. Then, the orthogonal encoding technique using DRPE is described in Section III. To show the effects of DRPE-based orthogonal encoding technique, simulation results are provided in Section IV. Finally, we conclude the paper with a summary in Section V.
II. DOUBLE RANDOM PHASE ENCRYPTION
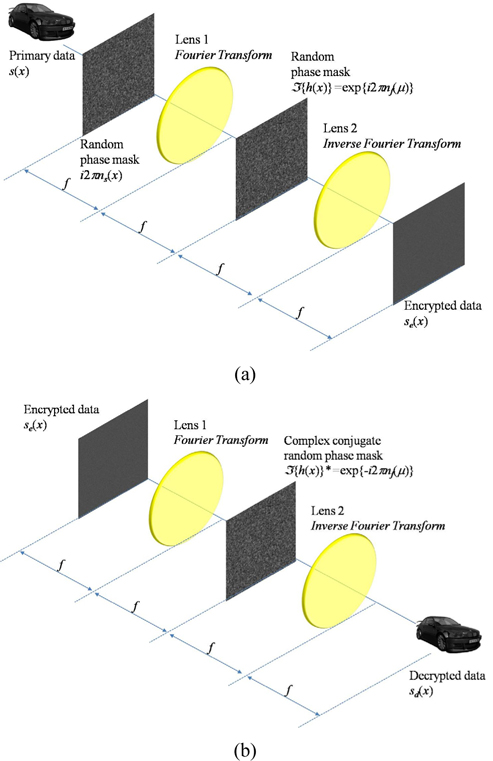
Optical encryption has many advantages such as the parallel processing of optical systems, the fast processing time, and the data handling in various domains. One of the optical encryption methods, double random phase encryption (DRPE), uses two sets of random phase information. Let us consider the encryption of a one-dimensional signal for simplicity. Figure 1(a) shows the optical schematic setup of DRPE for encryption. Let
where and mean Fourier transform and inverse Fourier transform, respectively. By the characteristics of complex-valued function, encrypted data has amplitude and phase, i.e.,
Figure 1(b) illustrates the optical schematic setup of DRPE for decryption. To decrypt the primary data, encrypted data as shown in Eq. (1) is multiplied by the complex-conjugate of the Fourier transform of
III. DRPE-BASED ORTHOGONAL ENCODING TECHNIQUE
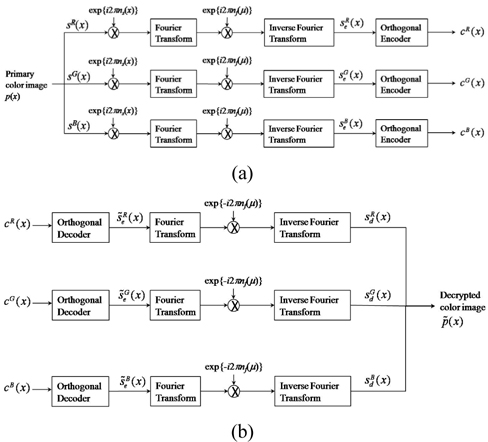
Figures 2(a) and (b) show the orthogonal encoding procedure using DRPE for encryption and decryption, respectively. As shown in Fig. 2(a), the primary color image,
To acquire the primary color image, first the three encoded data are independently decoded with the orthogonal property used in the encoder, and then the three decoded data, (
For orthogonal encoding and decoding, we use the Hadamard matrix of order 2, denoted by H2, with the orthogonal property as the following equation [21]:
where H2 =[1 1; 1 -1], I2 denotes the 2×2 identity matrix, and H
where
In the decoder, the real and imaginary parts of the encoded data,
where (
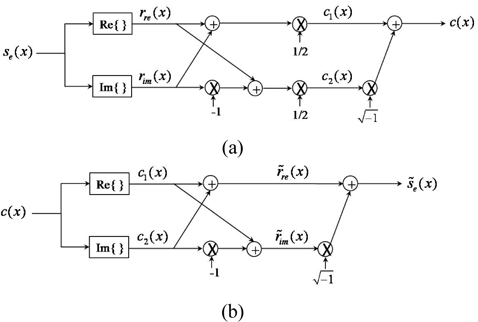
Figures 3(a) and (b) depict the linear operations of the encoder in Eq. (4) and the decoder in Eq. (5), respectively. As shown in these figures, the structures of the encoder and decoder are the same except for the normalization factor and consist of simple linear operations, so that the orthogonal encoder and decoder are easy to implement.
For simulations, we consider a color image with 1350(H) ×1350(V) pixels in Fig. 4. The color image is captured by digital camera with 50 mm imaging lens. Figures 4(a)~(d) show the primary color image and its separated color channel (R, G, and B) images, respectively. The primary color image and the three separated images correspond to
Figure 6 shows the decrypted images without decoding, by simulation. Figures 6(a)~(c) show the decrypted images of red, green, and blue channels without decoding, respectively. When no decoding is used, the complex-valued encoded data are directly decrypted, i.e., (
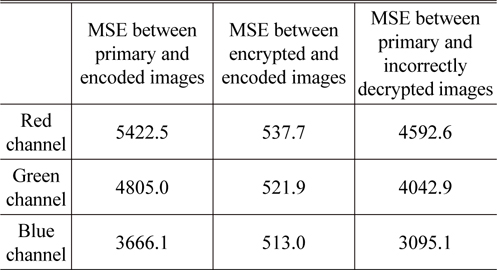
Table 1 shows mean square error (MSE) results for the images as shown in Figs. 4~6, where it is assumed that the pixel intensity (integer value) range of each image is from 0 to 255. The values of three different columns in Table 1 are MSE results between primary and encoded images, between encrypted and encoded images, and between primary and incorrectly decrypted images for red channel, green channel, and blue channel, respectively. From MSE results, it is illustrated that compared images are clearly different from each other.
[TABLE 1.] MSE results for the images as shown in Figs. 4-6
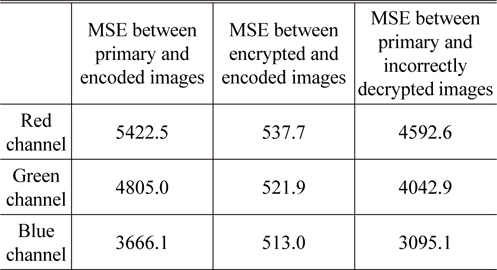
MSE results for the images as shown in Figs. 4-6
In this paper, we have proposed the DRPE-based orthogonal encoding technique for encryption of color images. To encrypt each of red, green, and blue components of a color image, the proposed orthogonal encoding technique employs DRPE with the same key and the orthogonal encoding scheme that uses the simple linear operations with a little complexity. Also, for decryption, we provide the orthogonal decoding scheme that has the same structure as the encoding scheme. The simulation results show that the proposed orthogonal encoding technique provides the powerful encryption effects in the absence of the orthogonal decoding although the key information of DRPE is perfectly known. Hence, the proposed orthogonal encoding technique can be used as a low-complexity and effective encryption technique for color images.