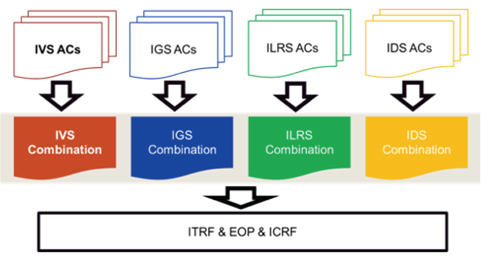
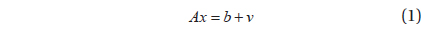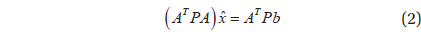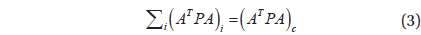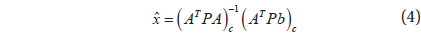For the last 10 years, global natural hazards such as large-scale earthquakes have frequently occurred. To investigate the cause of natural hazards and to prevent them, comprehensive understanding of the changes in the shape and rotation of the Earth is required. Accordingly, the importance of a high-precision reference frame has been emphasized. Space geodetic techniques precisely determine the terrestrial reference frame (TRF) and the earth orientation parameters (EOP) by observing celestial bodies or artificial satellites. The space geodetic techniques include very long baseline interferometry (VLBI), global navigation satellite system (GNSS), satellite laser ranging (SLR), and doppler orbitography and radiopositioning integrated by satellite (DORIS). With a single technique, there is a limit in determining perfect TRF and EOP. Thus, the International Earth Rotation and Reference System Service (IERS) combines the above four techniques to produce the international terrestrial reference frame (ITRF) and EOP (Angermann et al. 2004). Before the combination of the techniques, the International VLBI Service for Geodesy and Astrometry (IVS), International GNSS Service (IGS), International Laser Ranging Service (ILRS), and International DORIS Service (IDS), which are the services of the International Association of Geodesy (IAG), provide the representative combination solution of each technique to IERS (Fig. 1).
IVS generates the VLBI combination solution through combining products from various IVS analysis centers (ACs) (Fig. 1). Until recently, combination analysis has been performed using only DOGS-CS (Angermann et al. 2004). However, for a more accurate and reliable combination solution, the necessity of mutual verification using independent software has been suggested. Therefore, this study focused on the independent VLBI combination analysis using Bernese (Dach et al. 2007), which is the GNSS data processing software.
The combination for each technique, i.e. intra-technique combination, is a process in which the products that have been analyzed using the same data obtained from the same technique are combined. For intra-technique combination, the normal equation level combination method is commonly used (Vennebusch et al. 2007). Bernese has a normal equation combination program, and it can combine normal equations which consist of the parameters that Bernese can handle (e.g., station coordinates or earth orientation parameters), regardless of the types of techniques. In this study, the VLBI combination capability of Bernese was verified based on the results of the station coordinate time series and the combined TRF, which were obtained by the combination processing of VLBI products using Bernese. Also, the limitations of the VLBI combination analysis strategy using Bernese and suggestions for improvement were discussed.
The Astronomical Institute of the University of Bern (AIUB) has served as IGS AC since 1992, and developed Bernese, which is GNSS data processing software. Currently, Bernese supports not only the data processing of GNSS, but also that of other space geodetic techniques. In practice, ILRS AC uses Bernese for the SLR data processing (Richter & Mareyen 2012). Recently, GNSS satellite observation studies using VLBI have been performed (Tornatore & Haas 2010, Bar-Sever et al. 2011), and it is expected that these data can be easily processed using Bernese.
Bernese includes ADDNEQ2, which is a program that estimates parameters by combining a number of normal equations. This program can process normal equations which consist of the parameters that Bernese can handle, regardless of the types of techniques. The products that are provided by VLBI AC include station coordinates, nutation parameters, polar motion and its rate, and universal time (UT1) and length of day (LOD).
In this study, the combination processing of VLBI products was performed using Bernese 5.0. For this procedure, part of the Bernese source code and part of the VLBI Solution INdependent EXchange format (SINEX) file were modified to process the SINEX file which is the VLBI product format (Kwak & Cho 2011). However, the modified Bernese 5.0 was still limited in that it supports the calculation of the dψ and dε components, which are based on the equinox that is the intersection point between the celestial equator and the ecliptic, rather than the calculation of the nutation parameter dX and dY components, which are based on the celestial intermediate origin (CIO) that is the non-rotating origin of the Geocentric Celestial Reference System (GCRS). Therefore, in this study, for the ACs using dX and dY, nutation parameter components were pre-eliminated, and then combination processing was performed. Most IVS ACs provide the UT1 parameter in the form of the UT1-international atomic time (TAI). However, Bernese 5.0 supports only the UT1-coordinated universal time (UTC). There is an integer difference between TAI and UTC, which is as much as the leap seconds. Thus, when the normal equations of VLBI are imported, this difference should be corrected (transformed) before performing combination processing. However, in the current version of Bernese, UT1 correction is not considered. In Section 5, the effect of this on the VLBI combination processing results is discussed.
3. COMBINATION AT THE NORMAL EQUATION LEVEL
To analyze VLBI observation data, the least square method (LSM) is typically used. According to LSM, the normal equation is determined depending on the parameteer to be estimated, and includes the information on the observation model, weighting, and observables. If the observation model of VLBI is Eq. (1), the normal equation can be expressed as Eq.(2).
where
where
Using the combined normal matrix
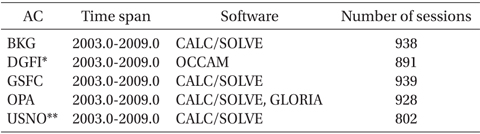
The combination analysis of products from five IVS ACs (Table 1) was performed on 943 sessions for 7 years (2003~2009). The session is the basic unit of geodetic VLBI observation, and one product isobtained per session. Each AC provides products in the SINEX format, which includes the estimated values of station position and earth orientation parameters; and the information on the normal equation for the parameters (Blewitt et al. 1994). The normal equation from each AC has different a priori value and epoch for the parameters. Therefore, for the combination of normal equations, the normal equations were transformed so that they could have common a priori value and epoch.
[Table 1.] IVS ACs which used in this study.
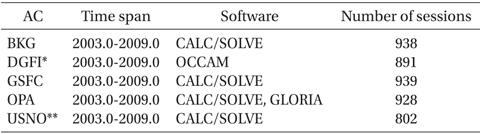
IVS ACs which used in this study.
Due to its observation characteristics, VLBI has only baseline information, which is the relative position among stations. Thus, position coordinates and Earth’s rotation cannot be determined using only the observation data. Accordingly, in the analysis process, constraints for them are added. The input data of combination processing, which is provided by IVS AC, is the datum-free normal matrix information in which constraints have been removed. Therefore, during the combination processing, parameters were estimated by applying common constraints to the normal equations of all the ACs.
Currently, Bernese uses dψ and dε values, which follow the IAU2000 model (McCarthy & Petit 2004) and are based on the equinox regarding nutation. However, in recent years, BKG, Goddard Space Flight Center (GSFC), and Paris Observatory (OPA) have provided products in the form of dX and dY, which are based on CIO. The determination of nutation parameters is the VLBI’s exclusive role, and in the combination process, it needs to be combined together with other parameters. However, the current version of Bernese is not able to estimate the nutation parameters of dX and dY. Thus, nutation terms were inevitably removed from the normal equations of BKG, GSFC, and OPA.
To examine the time series variation of the station coordinates, the normal equations of each AC, which had been transformed to have the same a priori value and epoch, were combined for each session. The a priori value of the coordinate was set to ITRF2008, and for the a priori value of EOP, the IERS 05C04 series was used. To define the datum, the minimum constraints of no-net-rotation/nonet- translation (NNR/NNT) for the 21 reference stations were given with respect to ITRF2008. The reference stations were selected depending on the observation frequency and geographic distribution. By extracting the result of a specific station from the combination solution for each session, the time series variation of the station coordinates could be examined. In this regard, the combination solution for each session did not include velocity information.
TRF is expressed as the set of station positions and velocities at a reference epoch. In this study, to determine TRF, the EOP parts were pre-eliminated from the normal equations of all the ACs for all the sessions, and only the TRF components were left. Then they were combined as one normal equation. For the combined normal equation, the a priori value and minimum constraints, which were identical to those used in the combination processing for each session, were applied. The reference epochs of the position coordinate and velocity of TRF, which are provided by ADDNEQ2, are the first session start time and the midpoint time of the entire period, respectively.
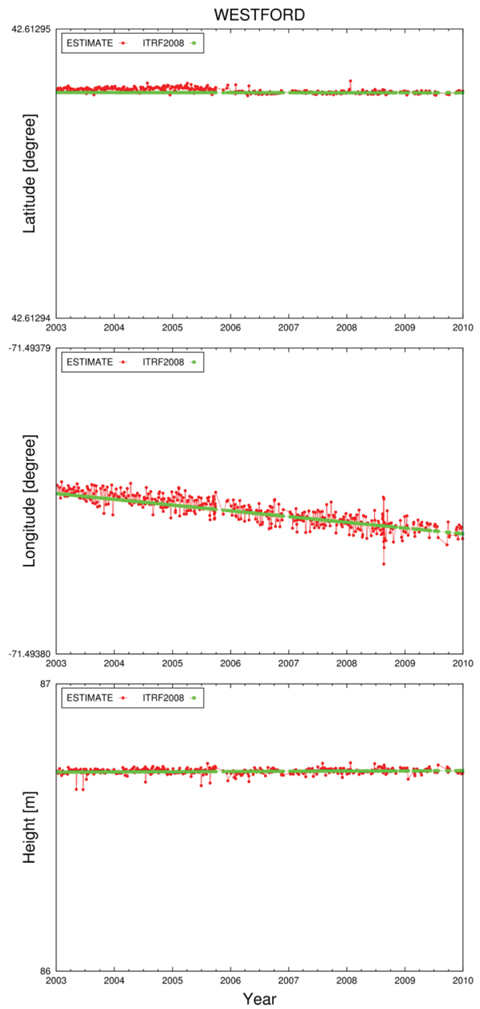
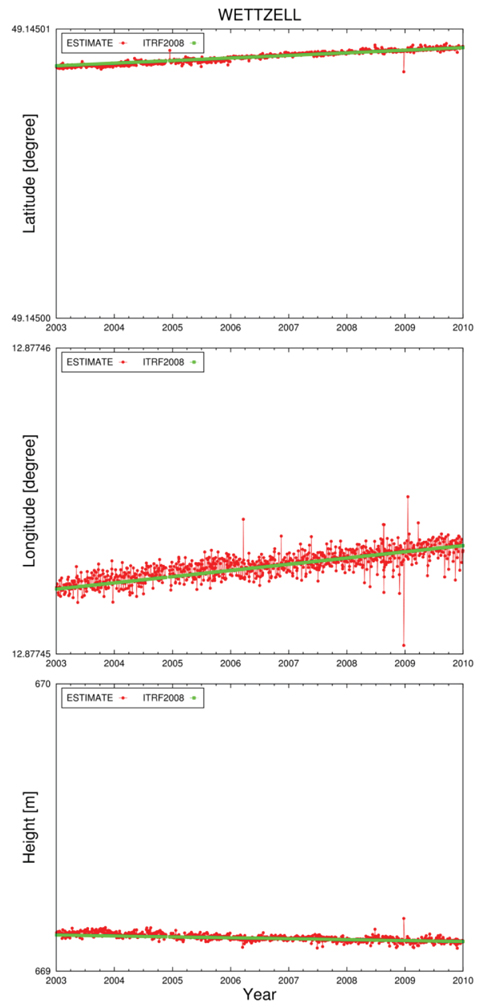
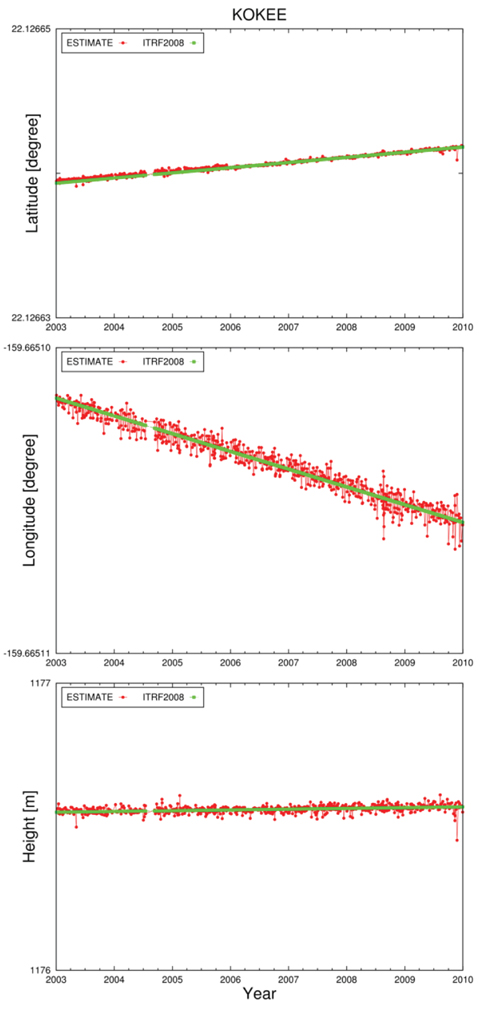
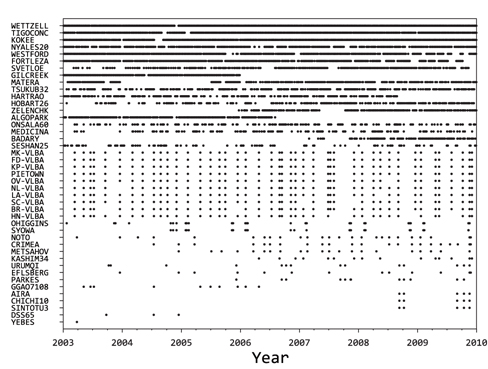
To verify the VLBI combination capability of Bernese, the station position coordinates for each session were estimated using the normal equations of each IVS AC summarized in Table 1. The positions of a total of 43 stations were estimated. The root mean square (RMS) errors of the latitude and longitude components were about 15.6 mm and 37.7 mm, respectively, and the error of the height component was about 30.9 mm, with respect to ITRF2008. Figs. 2-4 show the examples of the time series for the latitude, longitude, and height of the three stations (Westford, Wettzell, and Kokee), among the 43 stations. The above three stations had high observation frequencies from 2003 to 2009 (Fig. 5), and are thought to be stable because they have performed observation for a long time, from 1981, 1983, and 1993 to the present, respectively. In the figures, the red color represents the estimated value, and the green color represents the a priori value based on ITRF2008. For each plot, a single tic of the vertical axis corresponds to about 1 m. It was found that the errors of the longitude components were relatively larger than those of the latitude and height components.
Most VLBI results provide UT1-TAI values, but Bernese, which is the software for GNSS, can process only UT1- UTC values at the moment. Thus, for the normal equations of some ACs (BKG, GSFC, OPA, and USNO), which were entered in the software, the difference between the UT1- TAI and UT1-UTC values was included. UT1 is a parameter that represents the rotation of the Earth, and is correlated with longitude that has the same direction. Therefore, the UT1 errors of some ACs were included in the results of the longitude, and thus the longitude component showed larger RMS error than the latitude and height components. In the future, the software needs to be improved regarding the problem of UT1 correction.
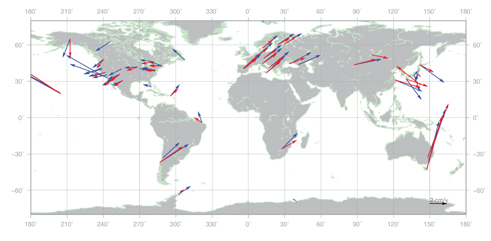
TRF was estimated by combining the normal equations of five ACs during 7 years (2003~2009) as one normal equation. Fig. 6 shows the velocity vectors of the combined TRF (red) obtained in this study and the ITRF2008 (blue). ITRF2008 is the result that combined the data from the four space geodetic techniques (GNSS, VLBI, SLR, and DORIS) which had been accumulated for 25 years (1984~2008). Thus, the stations, which had performed observation up to 2003, exist only on ITRF2008. The YEBES station in Spain dismantled the 14 m antenna that had been used from 1995 to 2003. Accordingly, as for the data from the YEBES station used for the combined TRF, the observation period was very short (less than 1 year), and thus the estimation of a proper velocity vector was not available (Fig. 5). Therefore, as shown in Fig. 6, it had completely different magnitude and direction, compared to the velocity vector on ITRF2008.
The velocity vector of the remaining 42 stations excluding the YEBES station in Spain showed a magnitude difference of 7.3 mm/yr (30.2%) and a direction difference of 13.8° (3.8%), with respect to ITRF2008. As for each continent, the 10 stations in Europe showed a magnitude difference of 7.8 mm/yr (30.3%) and a direction difference of 3.7° (1.0%), while the 14 stations in North America showed a magnitude difference of 2.7 mm/yr (15.8%) and a direction difference of 10.3° (2.9%). For South America, Australia, and Africa, the numbers of stations were 2, 2, and 1, respectively. As it was not possible to calculate statistics that have local representativeness, they were excluded from the statistics for each continent. Since the stations in Japan are located at the boundaries of four kinds of plates, the occurrences of earthquakes are frequent and the station positions are occasionally discontinuous. Accordingly, the estimated station velocities were not consistent, and thus there was a difference in velocity vectors between ITRF2005 and ITRF2008. Therefore, Asia including Japan was also excluded from the statistics for each continent. When compared with the result of Boeckmann et al. (2010), in which the magnitude difference in velocity vectors between the VLBI combined TRF and the ITRF was about 0.6 mm/ yr (3.1%), the result obtained in this study was about 10 times larger. Based on the bias for each continent and the large errors, it was found that bias errors were included in the velocity vector of the combined TRF, other than random errors. This is thought to be due to the longitude component error mentioned above. As there is a large error in the longitude component, the Helmert transformation, which represents the relation between TRFs, is not meaningful at the moment. Thus, it was not considered in the result of this study.
This study focused on developing a technique for VLBI combination using Bernese, and verifying the performance. The combination solution produced in this study was the time series of station coordinates and the combined TRF. The Bernese software is not able to estimate UT1-TAI components among VLBI products. Therefore, the longitude component, which has the same direction component as the UT1-TAI component, showed larger RMS errors than the latitude and height components. The analysis of the velocity vectors of the VLBI stations on the combined TRF indicated that the European continent and the North American continent showed differences in the magnitude and the direction, with respect to ITRF2008. This trend is thought to be due to the UT1 error, similar to the time series of the station position coordinates.
Until recently, the VLBI combination has been performed using single software. For the more accurate and reliable VLBI TRF, mutual verification is required using an approach that is differentiated from the existing method. This research is the first study that enabled the VLBI combination processing using the GNSS data processing software and verified the performance. The limitations of Bernese were analyzed, and suggestions for improvement could be found. In the future, for the improvement of the combination solution, Bernese needs to be updated so that it can handle various nutation models and UT1 parameters.