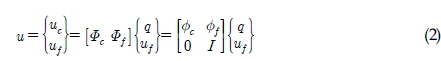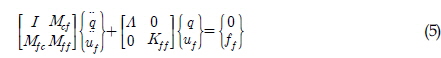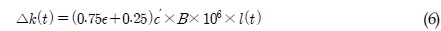In this study, a gearbox and blade were modeled in the MASTA program, and the housing and carrier components were modeled using a finite element method. Using substructure synthesis, all the components were combined and used to establish a vibration model of a 2.5-MW wind turbine gearbox. In addition, the safety displacement factor was evaluated using an AGMA data sheet about bearing's outer race for the input shaft and output shaft. As a result, the bearing's outer race for the input shaft, and the radial and axial responses were satisfied by the 1st and 2nd planetary gears and the 3nd helical gear transmission error(TE), respectively. However, the output shaft support bearing's outer race responses were not satisfied with the radial response by the 2nd TE and axial response by the 3rd TE. To reduce the vibration, tooth modification was needed. After profile tooth modification, at the outer race of the output shaft support bearing, the radial response was reduced by approximately 20μm, and the axial response was reduced by approximately 6μm.
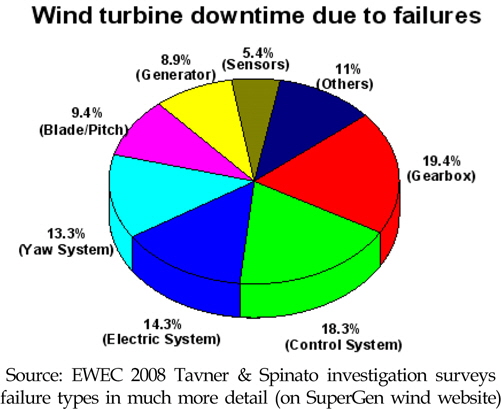
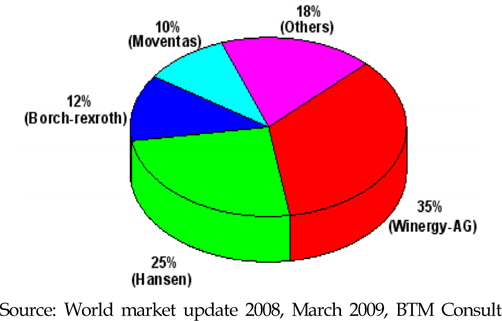
최신재생에너지의 수요증가로 인하여 풍력발전은 화력발전을 대체 할 수 있는 가장 보편화된 전력생산 방법으로 각광 받고 있다. 보다 큰 전력을 생산하기 위하여 풍력발전기는 대형화 추세이며, 소음/진동으로 인하여 민원이 발생이 많아서, 설치위치가 육상에서 해상으로 옮겨가고 있다. 풍력발전기는 회전자 블레이드로부터 저속, 고 토크 형태의 동력이 입력되면 이를 기어박스가 받아서 발전기에 고속 저 토크의 동력을 전달하는 형태로 되어 있어서, 특히 회전자블레이드의 정격 입력속도가 10~30rpm의 저속이지만, 발전기 출력속도가 1,200~1,800rpm의 고속을 요구하기 때문에 증속비가 50~150 정도의 비교적 큰 속도비를 요구하고 있다(Heier and Waddington, 2006). 특히 해상풍력발전기는 고 동력으로 인해 기어박스가 대형화 되고 있으며, 해상풍력발전기 입력축 정격 회전속도가 육상 풍력발전기보다 낮은 속도로 회전하므로, 더 높은 기어비를 구성해야 하기 때문에 기어박스 진동/소음을 고려한 설계 기술이 더욱 중요하다. 또한 해상풍력발전기의 안정성과 원가절감을 위해서, 기어박스의 무게를 경량화 시키기 위한 노력(Park and Lee., 2010)이 진행되고 있으며, 이로 인하여 진동/소음을 고려한 설계가 매우 중요해지고 있다. 이러한 기어박스 진동/소음을 고려한 설계기술 부족으로 인해, Fig. 1에서 보는 것처럼, 풍력발전기 파손이 기어박스가 19.4%로 가장 높고, Fig. 2에 의하면, 풍력발전기 기어박스 생산업체 점유율은 독일의 Winergy를 포함한 유럽의 4개 업체가 82%를 차지함을 알 수 있다.
풍력발전기의 기어박스에 대해 많은 연구가 수행되고 있다. 블레이드, 증속기를 포함한 풍력발전시스템의 비틀림 진동해석을 수행하였으며(Todorov and Vukov, 2011; Kim et al., 2012), 정상풍속과 돌발풍속을 수학적으로 모델링하고 풍향에 따라 전달되는 메인축에서의 전달모멘트를 조사하여 기어박스에 전달되는 풍하중 특성을 파악하였다(Kim et al., 2012). 풍력발전용 기어박스의 비틀림 진동 모델을 수립하여 비틀림 진동특성을 분석 연구하였다(Kim et al., 2011). 풍력발전시스템 기어트레인의 설계요구조건을 광범위하게 고려하여, 1M~8M 풍력발전기 기어트레인의 특성분석을 하였다(Park and Lee., 2010). 풍력발전기 시스템용 기어박스를 부분구조합성법을 이용하여 풍력시스템의 특성분석을 하였다.(Peeters, 2006). 풍력발전기 시스템을 유한요소법으로 모델링을 하여 구조물 소음, 공기음에 대해서 연구하였다(Vanhollebeke et al., 2012). 이와 같은 연구사례를 살펴보았을 때, 풍력발전용 기어박스자체의 응답특성을 통한 안정성평가에 대한 연구는 미흡한 실정이다.
본 연구에서는 유성기어시스템, 헬리컬기어시스템, 블레이드 등을 SMT(Smart Manufacturing Technology)사에서 개발한 풍력발전기용 기어박스 전용소프트웨어인 MASTA(SMT, 2010) 프로그램으로 모델링하고, 기어박스 하우징, 토크암, 유성캐리어를 유한요소법으로 모델링하였다. 부분구조합성법으로 MASTA의 모델과 유한요소모델을 조합하여 2.5MW 풍력발전기용 기어박스에 대한 동특성 해석을 수행하였다. 또한 1단, 2단 유성기어시스템 및 3단 헬리컬기어 시스템의 기어 치합전달오차에 의한 가진원을 모델링하였다. 또한 치합전달오차 가진에 의한 입력축 베어링 외륜지점과 출력축 베어링 외륜지점에 변위를 AGMA 6000-B96(AGMA, 1996)의 데이터시트를 이용하여 진동의 안전성 평가를 수행하였다. 문제가 발생한 출력축 베어링 외륜지점에 대해서, 치형수정을 통한 진동저감대책을 제시하였다.
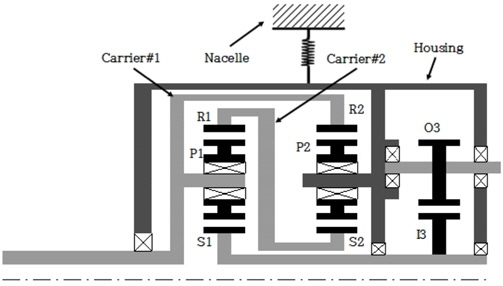
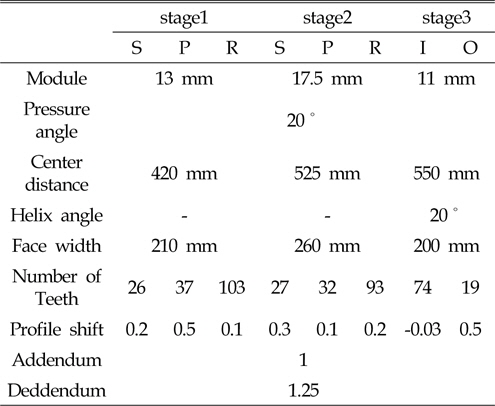
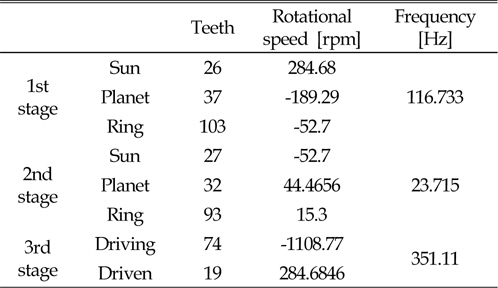
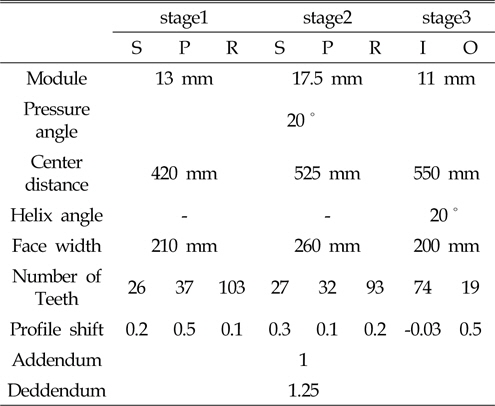
본 논문의 연구 대상은 2.5MW급의 풍력발전기용 동력분기식 기어박스이며, Fig. 3과 같이 2단의 유성기어단과 1단을 헬리컬 기어단으로 이루어져 있다. 메인축(입력축)을 통하여 1단 유성 기어단의 캐리어와 2단 링기어로 입력이 되며, 2단 캐리어는 하우징에 고정 되어 있다. 2단 선기어는 1단의 링기어와 연결되어 있으며, 1단 선기어는 3단 헬리컬 기어단의 구동기어와 결합이 되어 있다. 또한 기어박스는 6° 기울어진 상태로 너셀에 결합되어 있다. 기어열의 제원은 Table 1에 나타내었다. 아래 그림의 첨자
Gear information
본 연구에 사용된 풍력발전 시스템은 블레이드와 기어박스의 입력축은 플랜지 결합으로 이루어져 있으며 기어박스 출력축은 발전기와 커플링으로 결합되어 있는 구조이다. 하우징은 양쪽 토크암 마운트에 의해서 지지가 되어 있으며, 메인축은 메인 베어링에 의해서 지지되어 있다. 유성기어시스템, 헬리컬기어시스템, 축, 베어링요소와 같은 동력전달부분은 MASTA 프로그램을 통하여 모델링 하였으며, 기어박스 하우징, 토크암, 유성캐리어, 플랜지 부분 등은 유한요소법으로 모델링하여 부분구조합성법을 통하여 전체 시스템을 모델링 하였다. 유한요소모델을 그대로 사용하면 질량, 강성 행렬의 사이즈가 비대하게 크기 때문에 해석시간, 컴퓨터 메모리 사용에 단점이 있다. 이를 보완하기 위하여 부분구조합성법을 사용하였다. 부분 구조합성법을 사용하연 거대한 사이즈의 행렬이 설정한 노드 사이즈로 축소를 할 수 있다. 부분구조합성법인 Component mode synthesis(CMS)는 고유모드, 강체모드, 변형모드를 일반화된 자유도로 이용하였으며(Hurty, 1960), 강체운동 모드와 변형모드를 Craig-Bampton방법으로 일반화 되어 사용되고 있다.(Craig and Bampton, 1968) 아래 수식은 이를 간략히 정리한 것이다.
위의 식은 다음과 같이 변환 시킬 수 있다. 아래첨자가
여기서, 이다. 식 (5)에서 자유도가 경계 및 내부노드로 축소된 것을 확인 할 수 있다. 이와 같이 부분구조 합성법을 통하여 유연체의 질량, 강성행렬의 사이즈를 축소하여 기어트레인과 결합할 수 있다.
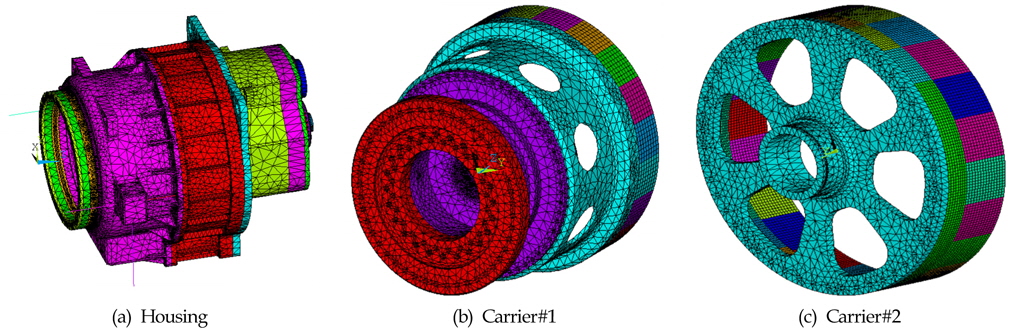
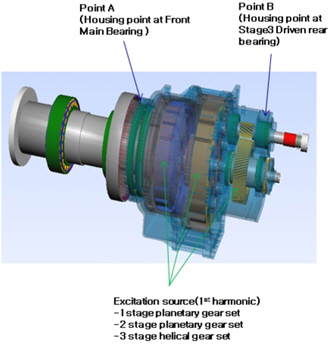
풍력발전용 기어박스의 경우는 하우징이 너셀에 토크암 마운트로 지지되어 있는 특이한 조건이기 때문에 토크암 마운트를 고려한 설계를 하는 것이 중요하다. 토크암 마운트에 토크암 강성과 동일한 스프링을 연결하여 너셀에 지지 효과를 주었다. Fig. 4는 하우징, 캐리어의 유한요소 모델이다. 하우징, 캐리어#1, 캐리어#2는 ANSYS에서 solid 186,187요소를 사용하여 요소화 하였으며, 각각은 297196개, 304321개, 189146개의 절점과 181173개, 188988개, 52286개의 요소를 사용하였다.
하우징은 Table 2는 토크암 마운트의 강성값을 나타낸 것이다.
[Table 2] Torque arm stiffness information

Torque arm stiffness information
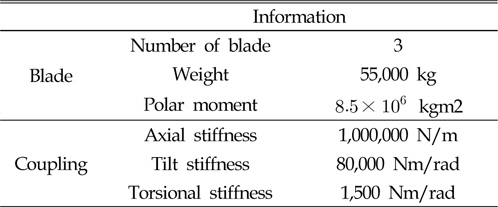
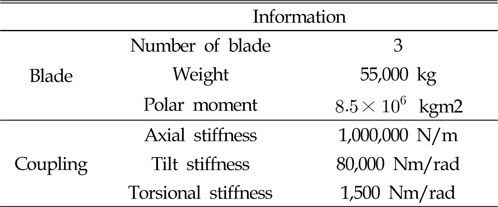
풍력발전용 기어박스의 진동 특성을 파악하기 위해서는 기어박스 뿐만 아니라 기어박스와 연결되어 있는 입력축과 출력축 부분의 모델링이 포함되어야 한다. 입력축에는 블레이드에 해당하는 질량과 관성모멘트를 가지는 디스크, 출력축에는 발전기 회전자의 관성모멘트를 가지는 디스크를 모델링하여 관성모멘트에 대한 효과를 부여하였다. 또한 출력축은 고속커플링으로 회전자와 연결되어 있다. Table 3은 블레이드, 발전기 회전자 및 커플링의 정보이다. Fig .5는 기어박스 시스템의 전체 형상을 나타 낸 것이다.
[Table 3] Blade and coupling information
Blade and coupling information
풍력발전기용 기어박스의 소음을 일으키는 주원인은 기어박스에 하중이 가해질 때, 치합전달오차에 의해 치충돌을 발생하여 소음을 발생하게 된다. 따라서 치합전달 오차에 의한 특성을 살펴보기 위하여, 치합전달 오차의 가진원에 대한 모델링을 수행하여야 한다. 치합전달오차의 발생원인 및 발생인자에 대해 Table 4에 나타내었다. 치합전달오차는 주로 축어긋남, 기어편심, 와블 등의 설치오차와 기어 가공오차, 부하에 의한 치변형에 의해 발생을 한다. 풍력발전기는 고동력이 작용하므로, 가공오차, 설치오차의 영향보다는 치합시 부하로 인한 치의 변형량에 의해 치합전달오차가 크게 발생하게된다(Lee and Kang, 2014).
[Table 4] Generation factor and causes of transmission error

Generation factor and causes of transmission error
본 연구에서는 가공, 설치오차에 의한 영향은 무시하고, 전달하중에 의한 치변형이 원인이된 치합전달오차을 구하였다. 기어가 물리고 있는 상태에서 작용선 방향으로의 두기어의 치변형량을 구하기 위해서는 치강성을 구하여야 한다. 치강성은 아래의 수식을 통해서 구할 수 있다(ISO, 2006).
여기서 은 Single stiffness이고
[Table 5] Transmission error harmonic component

Transmission error harmonic component
강제진동의 경우 감쇠에 의해서 그 크기가 변화가 심하다. 그래서 적절한 감쇠를 주어야지만 신뢰할 만한 결과를 얻을 수 있다. 하지만 감쇠는 주파수,동적 조건에 따라서 감쇠계수가 변하기 때문에 정확한 감쇠 효과를 부여하는 것은 쉽지 않다. 복잡한 시스템의 경우 비례감쇠를 이용하여 시스템감쇠를 적용하는 것이 일반적이다. 비례감쇠행렬[
여기서 계수 𝛼, 𝛽는
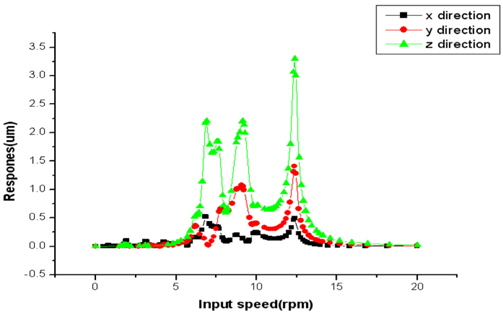
MASTA를 이용하여 각단의 1차 치합전달오차 하모닉성분을 가진원으로 하여 시정계-선형 시스템에서 강제진동해석을 수행하였으며 기어박스의 응답특성에 대해서 살펴보았다. 응답은 입력축 및 축력축 베어링의 외륜을 측정 지점으로 하였다. 기어박스의 진동측정은 베어링 주위의 하우징에 센서를 설치하여 측정을 하므로 응답을 베어링 외륜으로 하는 것이 타당하다. Fig. 7은 가진원과 측정위치를 나타낸 것이다.
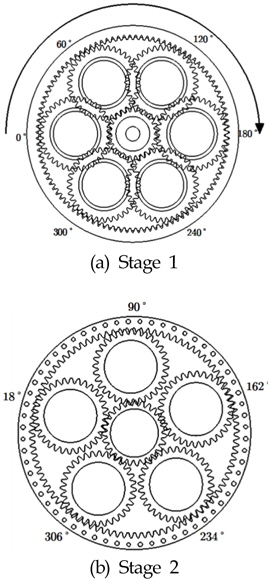
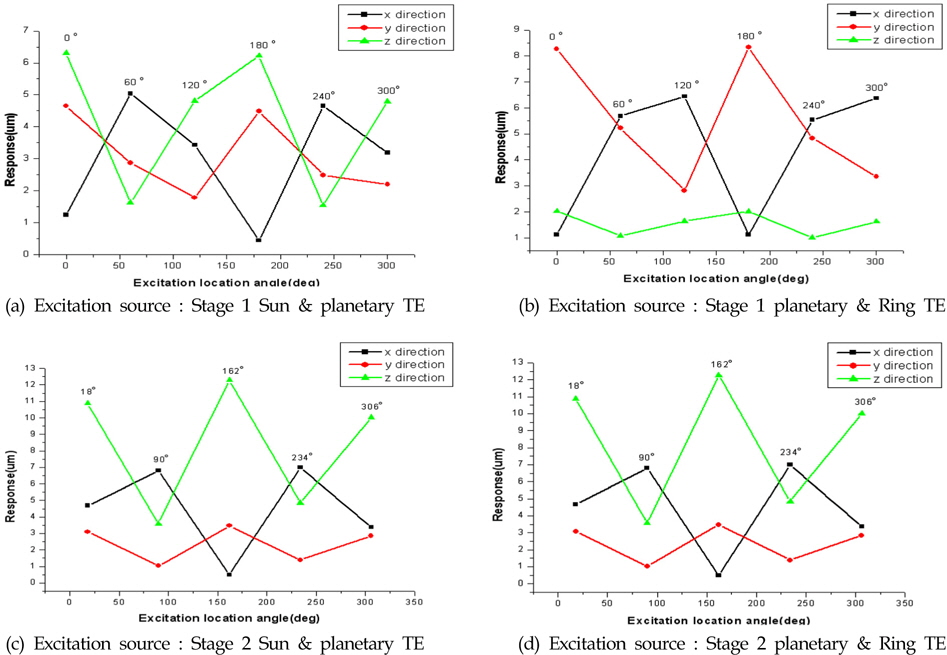
Fig. 8은 1단, 2단 유성기어시스템의 가진 위치에 따른 응답위치를 나타낸다. Fig. 6(a)는 1단 유성기어를 나타내고, 캐리어가 회전함에 따라 유성기어의 가진 위치가 변화하게 된다. 가진 위치를 0°, 60°, 120°, 180°, 240°, 300°로 변화를 주며 응답을 파악하였다. Fig. 6(b)는 2단 유성기어를 나타내고, 캐리어가 하우징에 고정되어 회전을 하지않는다. 유성기어의 가진 위치를 18°, 90°, 162°, 234°, 306°일 때 응답을 파악하였다.
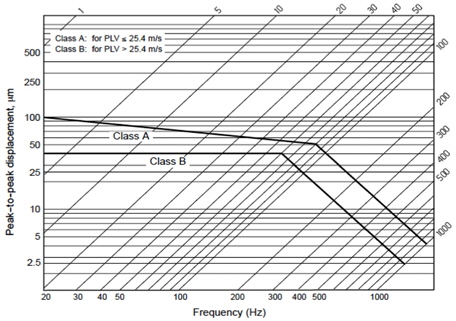
풍력발전기 기어박스 강제진동 해석을 통한 응답의 결과에 대한 평가를 하기위해, 실험평가에 사용되는 AGMA 6000-B96의 허용치를 기준으로 평가를 하였다(AGMA, 1996). Fig. 9는 변위의 허용치를 나타낸 그래프이다.
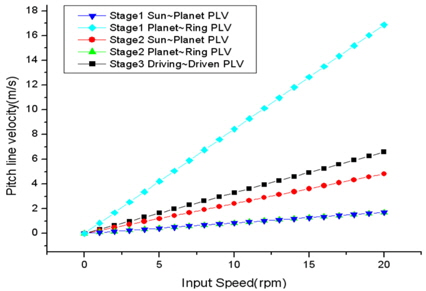
기어의 피치선속도(Pitch Line Velocity:PLV)는 기어의 회전속도(
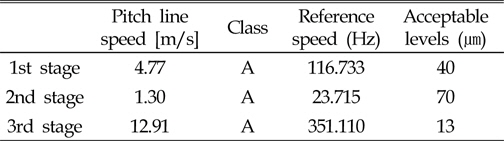
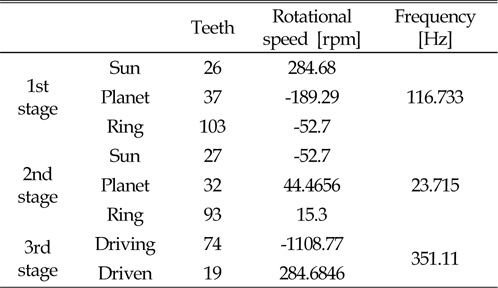
Table 6는 각 기어단의 회전속도와 15.3rpm기준으로의 가진 주파수를 분석한 것이다. 이 값을 기준으로 하여 변위허용치를 Fig. 9를 통하여 구하였다. Table 7은 Fig. 9를 통하여 구한 변위허용치를 나타낸다. 1단의 치합전달오차로 가진을 주었을 때, 측정지점에서 변위가 40㎛이하가 되어야하며, 2단 및 3단은 각각 70㎛, 12㎛이하의 변위를 가져야한다.
[Table 6] The speed and frequency of gear stage
The speed and frequency of gear stage
[Table 7] Acceptable levels of displacement at gear stage
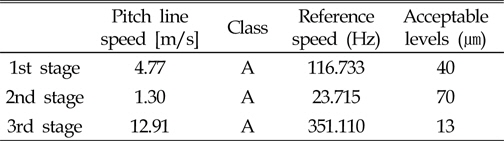
Acceptable levels of displacement at gear stage
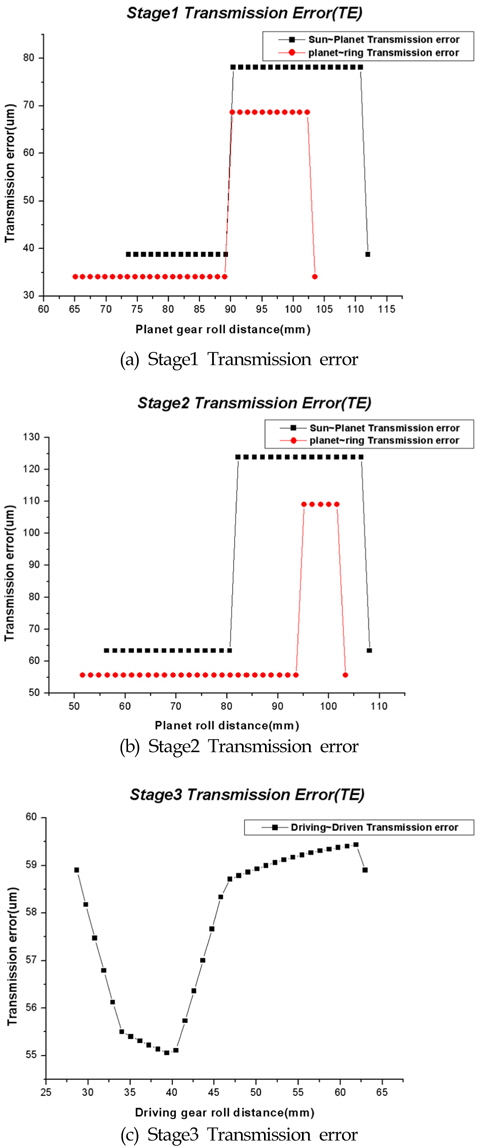
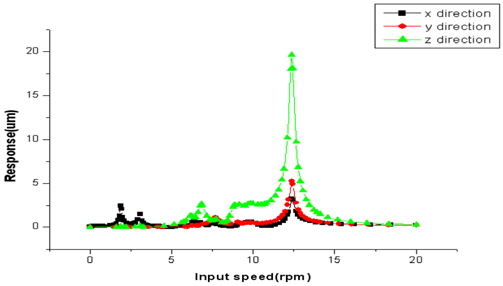
Fig. 11는 1단, 2단 유성기어시스템의 가진위치에 따른 관측지점 A의 병진응답 변화를 나타낸 것이다. Fig. 11(a)는 1단 선기어/유성기어의 치합전달오차 가진에 의한 0°, 60°, 120°, 180°, 240°, 300° 위치의 변위 응답을 나타낸다. 180° 위치에서
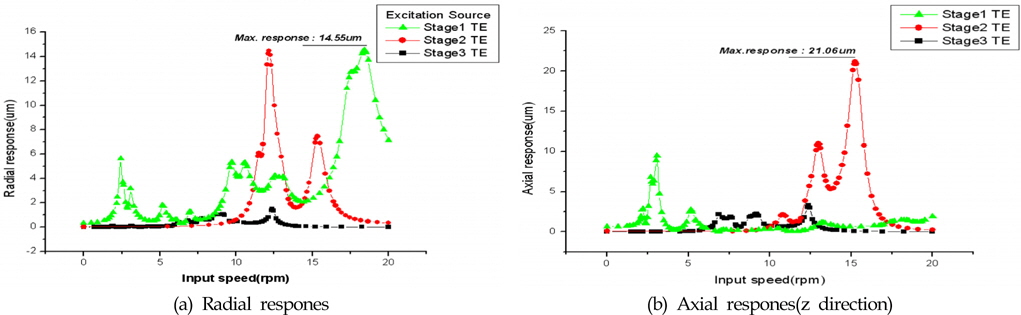
Fig. 13은 1단, 2단의 선기어/유성기어/링기어의 물림에서 발생하는 가진 및 3단 헬리컬기어단의 가진을 모두 고려하였을 때, 관측지점 A점의 반경방향 및 축방향 변위 변화를 나타낸 것이다. Fig. 13(a)의 반경방향에서는 2단 유성기어단의 응답이 가장 크게 나타났으며, 최대치가 약 15㎛정도 나타나고 있다. 허용 변위 값 70㎛이하임으로 안전함을 알 수 있다. Fig. 13(b)의 축 방향에서도 2단 유성기어단의 응답이 가장 크게 나타났으며, 최대치가 약 21㎛정도 나타나고 있다. 허용 변위 값 70㎛이하임으로 안전함을 알 수 있다. A지점의 응답특성을 보면, 모두 허용치를 만족함을 알 수 있다.
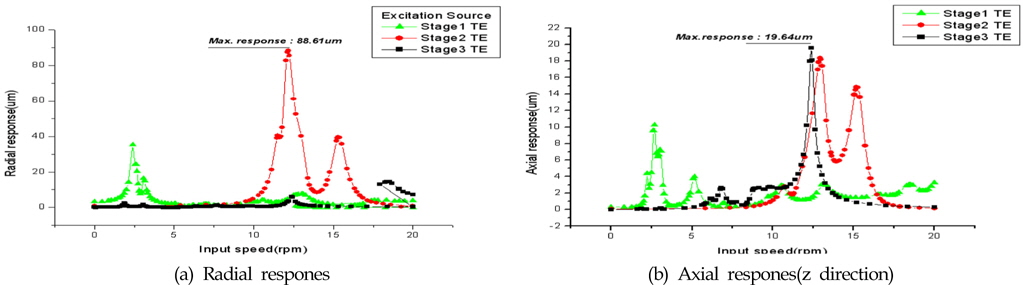
Fig. 14는 1단, 2단 유성기어시스템의 가진위치에 따른 관측지점 B점의 병진응답 변화를 나타낸 것이다. Fig. 14(a)는 1단 선기어/유성기어의 치합전달오차 가진에 의한 0°, 60°, 120°, 180°, 240°, 300° 위치의 변위 응답을 나타낸다. 60° 위치에서
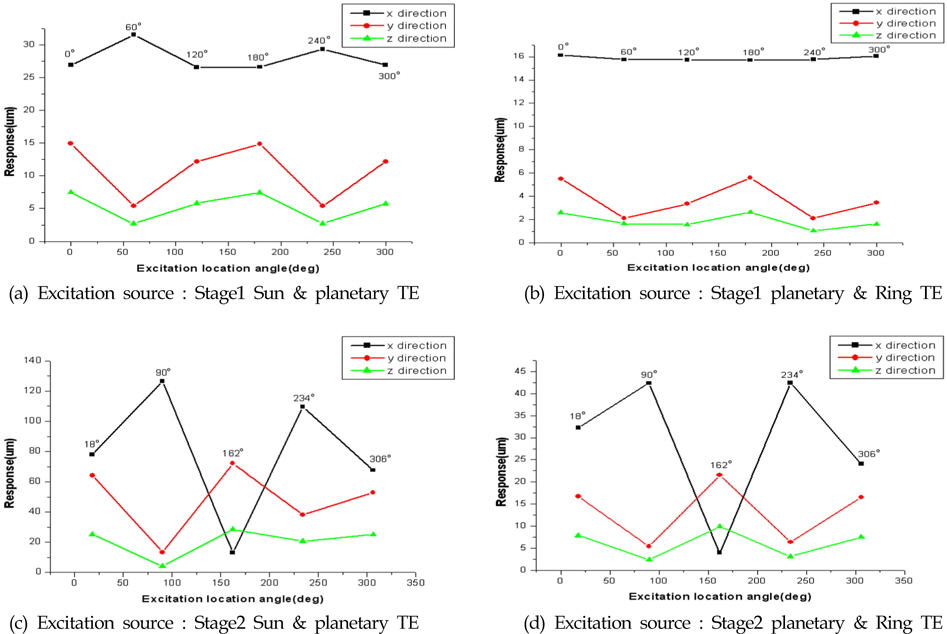
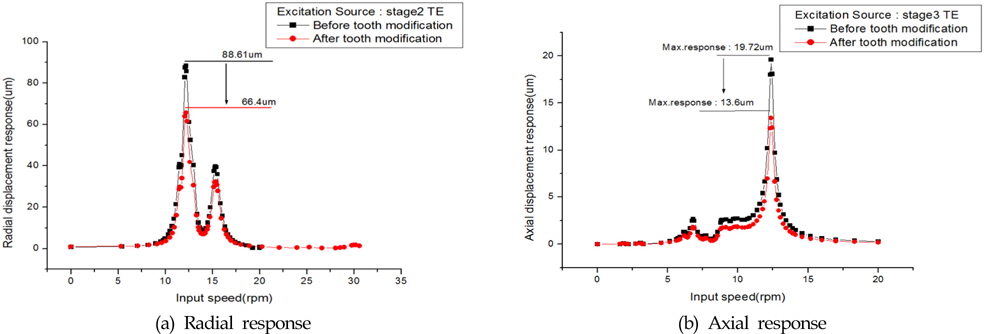
Fig. 16은 1단, 2단의 선기어/유성기어/링기어의 물림에서 발생하는 가진 및 3단 헬리컬기어단의 가진을 모두 고려하였을 때, 관측지점 B점의 반경방향 및 축방향 변위 변화를 나타낸 것이다. Fig. 16(a)의 반경방향에서는 2단 유성기어단의 응답이 가장 크게 나타났으며, 최대치가 약 89㎛정도 나타나고 있다. 허용 변위 값 70㎛보다 큼으로 저감대책이 필요함을 알 수 있다. Fig. 16(b)의 축 방향에서도 3단 유성기어단의 응답이 가장 크게 나타났으며, 최대치가 약 20㎛정도 나타나고 있다. 허용 변위 값 12㎛보다 큼으로 저감대책이 필요함을 알 수 있다.
B지점의 응답특성이 허용치를 만족하지 못함으로, 저감대책으로 치형수정이 필요하다. 치형수정은 치변형에 의하여 발생하는 변형량을 바탕으로 치형수정을 하였다(MAAG, 1990). 치변형량은 기어의 이접촉 개수가 변하는 Highest point of single tooth contact(HPSTC) 헬리컬기어는 Highest point of double tooth contact(HPDTC)에서 산출하였다. 치형수정은 Tip relief로 하였으며 HPSTC/HPDTC에서 치형수정을 시작하였다.
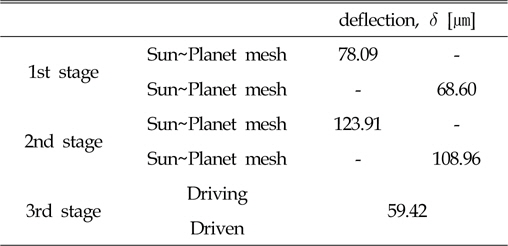
Table 8은 1, 2, 3단 기어 쌍의 프로파일방향 치변형량을 나타낸 것이다.
[Table 8] Amount of tooth deflection
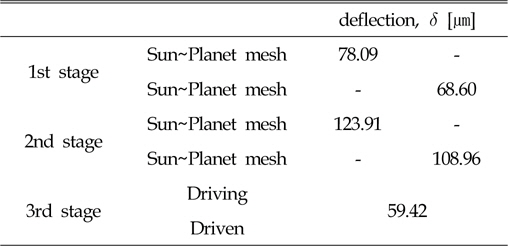
Amount of tooth deflection
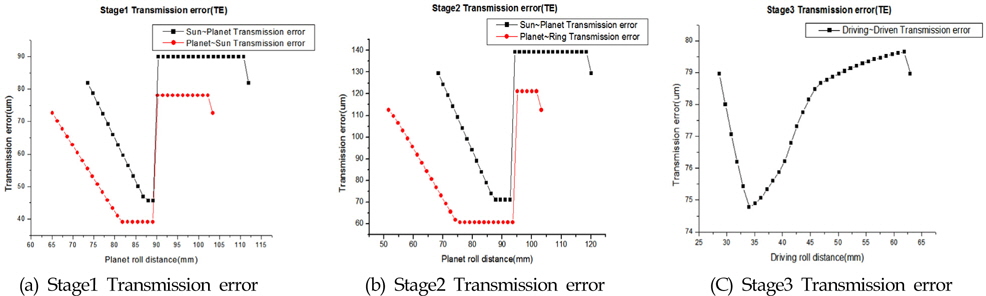
Fig. 17은 치형수정 후의 치합전달오차를 나타낸다. 치형수정 후 관측지점 B에서 허용치를 초과한 2단 치합전달오차에 의한 반경방향 응답과 3단 치합전달오차에 의한 축 방향 응답을 재해석 하였다. 이때의 치형수정 전과 후의 응답치를 Fig. 18에 나타냈다. 반경방향 응답을 살펴보면 최대 응답치가 약 20㎛가 감소한 65㎛로 떨어졌다. 치형수정을 통하여 허용치인 70㎛보다 낮아 진 것을 확인 하였다. 축 방향의 응답도 약 6㎛가 감소하여 최대 응답치가 약 13.6㎛이 되었다.
본 논문에서는 유성기어시스템, 헬리컬기어시스템, 블레이드 등은 MASTA 상용프로그램으로 모델링하고, 기어박스 케이스, 토크암, 유성캐리어는 유한요소법으로 모델링하였으며, 부분구조합성법으로 조합하여 2.5MW 풍력발전기용 동력분기용 기어박스에 대한 진동모델을 수립하였다. 또한 1단, 2단 유성기어시스템 및 3단 헬리컬기어 시스템의 기어 치합전달오차에 의한 가진원을 모델링하였다. 또한 입력축 베어링 외륜지점(Point A)과 출력축 베어링 외륜지점(Point B)에 변위에 대하여, AGMA의 데이터시트를 이용하여 진동의 안전성 평가를 수행하여 다음과 같은 결론을 얻었다.
(1) 입력축 베어링 외륜지점에 대해서, 1단, 2단 유성기어시스템과 3단의 헬리컬기어시스템의 반경방향 및 축 방향 허용 변위 값을 모두 만족하여 안전함을 알 수 있었다. (2) 출력축 베어링 외륜지점에 대해서, 2단 유성기어단의 반경방향의 응답의 최대치가 89.6㎛가 되어 허용치 70㎛보다 큼을 알 수 있었다. (3) 출력축 베어링 외륜지점 3단 유성기어단의 축 방향 응답의 최대치가 약 19.6㎛가 되어 허용치 12㎛보다 큼을 알 수 있었다. (4) 1단, 2단, 3단 각각의 기어에 대해 프로파일 치형수정을 실시한 결과, 출력축 베어링 외륜지점에 대해서, 2단 유성기어단의 반경방향의 응답의 최대치가 20㎛ 떨어져서 66.4㎛이 되어 허용치를 만족하였다. 또한 3단 유성기어단의 축 방향 응답의 최대치가 약 6㎛가 감소함을 알 수 있었다. (5) 풍력발전기는 비틀림진동으로 인해, 다른 산업용 기어박스보다 축, 케이스의 변형이 크게 발생함으로, 기어 리드방향의 치형수정에 대한 연구가 필요하며, 리드방향의 치형수정을 하면 2단, 3단 기어시스템의 허용치를 많이 감소시킬 수 있을 것으로 사료된다.