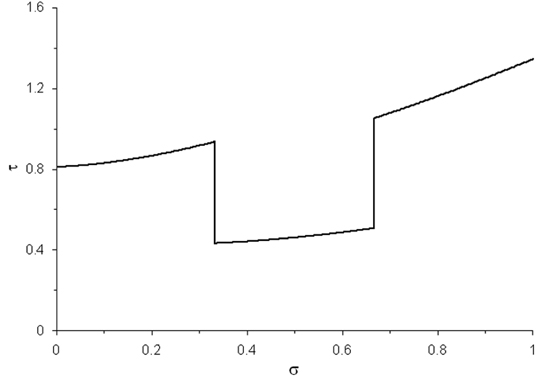
Ai : 비인장 상태 요소 케이블 i의 단면적 Ã : 인장 상태 케이블의 단면적 Ei : 요소 케이블 i의 영률 L : 비인장 상태 복합 케이블의 총길이 Li : 비인장 상태 요소 케이블 i의 길이 li : 비인장 상태 요소 케이블 i의 무차원화된 길이 mi : 비인장 상태 요소 케이블 i의 단위길이 당 질량 s: 비인장 상태 케이블의 원호길이 : 인장 상태 케이블의 원호길이 T : 케이블 장력 W : 복합 케이블의 총 자중 : 변형에 의한 케이블 단면적 비 βi : 요소 케이블 i의 Flexibility factor θ : 케이블 접선각 νi : 요소 케이블 i의 포와송비 (𝜉, η , ζ) : 무차원화된 케이블 형상 좌표값 ρi : 요소 케이블 i의 무차원화된 단위길이 당 자중 𝜎 : 비인장 상태 케이블의 무차원화된 원호길이 : 인장 상태 케이블의 무차원화된 원호길이 τ : 무차원화된 케이블 장력 φi- 1 : 요소 케이블 i의 평면 투영선과 x축과의 사이각
케이블 구조물은 장력만으로 하중을 지탱하는 케이블을 이용한 구조물로 건축, 토목, 조선해양 분야에 널리 사용되는 구조물 형식 중 하나이다(Irvine, 1981; Samset, 1985; Berteaux, 1976). 케이블 구조물은 설치 및 제거가 쉽고 강체구조물보다 비용이 저렴하다는 장점을 가진다. 그러나 케이블의 유연성으로 인해 하중에 대한 변위가 상대적으로 크고, 압축력에 저항 할 수 없으며, 허용 하중이 일반적인 강체구조물 보다 작다는 단점이 있다.
이러한 케이블 구조물의 해석을 위해서는 케이블 자중을 포함한 하중에 따른 형상해석이 필요하며, 케이블의 장력과 형상은 이 두 물리량의 상호작용에 의해 결정되는 비선형성이 강한 구조물이다. 케이블 자중에 의한 장력 및 형상은 현수선방정식으로 표현되며 Irvine(1981)과 Berteaux(1976) 등의 서적에 상세히 설명되어있다.
자중 뿐 만 아니라 집중하중이 부과된 케이블 문제의 경우, Irvine and Sinclair(1976)는 2차원 균일 탄성 케이블에 수직집중하중이 가해진 문제에 대하여 해석하였고, Sinclair and Hodder (1981)은 앞의 해석법을 케이블 네트워크의 해석에 적용하였다. Simith and MacFarlane(2001)은 수중에서 터치다운 포인트를 가지며 두 개의 상이한 케이블들로 구성된 복합 계류케이블에 하나의 부이 또는 싱커가 부착된 경우에 대하여 해를 다항식으로 변환하여 해석하였다. 수직 집중하중 뿐 만 아니라 수평 집중하중도 고려하게 되면 케이블 형상은 3차원 공간에서 해석하여야 하는데 균일 탄성 케이블에 대해서는 Peyrot and Goulois(1979), Such et al.(2009), Impollonia et al.(2011) 등의 연구결과가 있다.
본 연구에서는 상이한 물성을 갖는 요소 케이블들로 구성된 하나의 양단 고정 복합 케이블(Multi-component cable)에 3차원 정적 집중하중들이 작용하는 경우에 대하여 해석하였다. 케이블의 형상, 장력, 인장변형 그리고 단면의 수축변형에 대한 해들을 해석적으로 표현하였다. 그리고 몇 가지의 경우에 대한 적용 예를 수록하였다.
하나의 복합 케이블은 물성이 다른
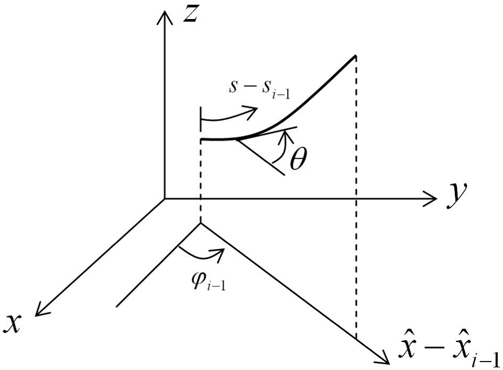
먼저 Fig. 1과 같이 절점
여기서
한편 장력에 의한 케이블 i의 수축된 단면적
여기서
해석의 편의를 위해 다음과 같은 무차원화 된 값들을 도입한다.
여기서
이러한 무차원화 된 값들을 사용하여 식 (1)과 (2)를 다시 표현하면 다음과 같다.
기하학적 적합조건은 다음 식으로 표현 된다.
식 (6)-(8)의 해는 잘 알려진 탄성 요소 케이블 i에 대한 현수선 방정식으로 다음 식들로 표현된다.
이 식들에서 밑 첨자와 윗 첨자가 함께 사용된 와 는 각각 요소 케이블 i의 시작점인 절점
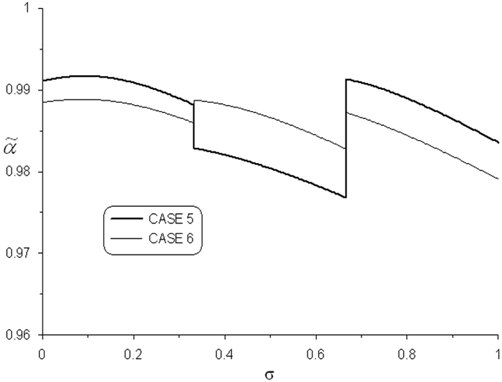
식 (3)의 단면적비 는 다음 식과 같다.
식 (9)-(13)로 표현된 해들에서 Flexibility factor인
절점 i에 복합 케이블 총 자중
여기서 i=1~
의 관계식들과 식 (14)-(16)을 결합하면 임의 절점 및 복합 케이블 끝점에서의 장력
위의 식들에서 i=1~n 이고, 특히 은 복합 케이블 끝점에서의 값들을 의미한다. 그리고 시작점으로 부터 첫 번째 요소 케이블에서는 다음의 관계식을 가진다.
식 (19)-(24)를 사용하면 절점 i에서의
한편 절점에서 형상의 연속성을 사용하면 다음과 같은 식들 을 얻을 수 있다.
여기서
복합 케이블의 양 끝단의 위치가 주어져 있으므로
세 개의 미지 값 ( )이 결정되면 식 (19)-(24)에 의해 모든 절점에서의
여기서
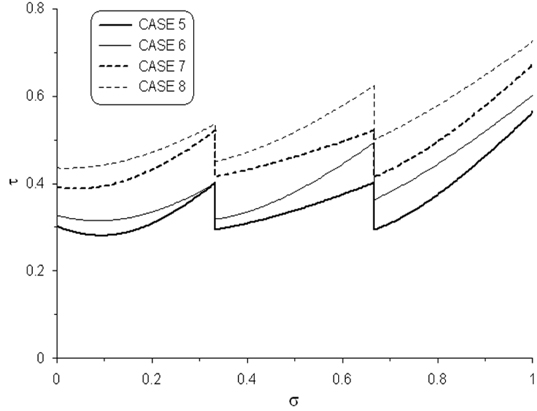
장력
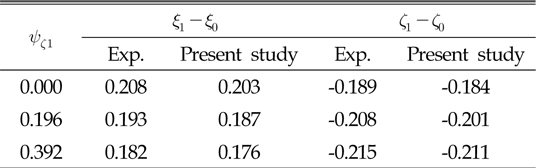
해석법의 유효성을 검증하기 위해 Irvine and Sincliar(1976)에 나와 있는 2차원 문제에 대한 실험치와 비교하였다. 상기 문헌 에는 균일한 탄성 케이블의 한 지점에 수직 집중하중을 가했을 때의 실험결과가 나와 있는데, 집중하중 작용지점은
[Table 1] Comparison between the results of experiment and present study
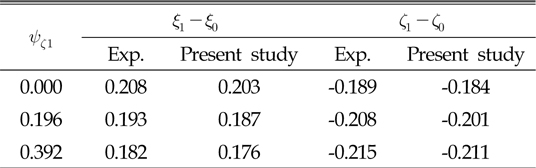
Comparison between the results of experiment and present study
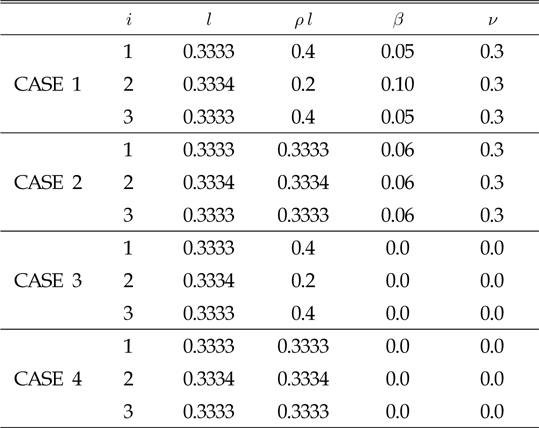
Table 2의 제원을 가지는 복합 케이블에 집중하중이 작용하 지 않을 때의 2차원 문제에 대하여 해석을 수행하였다. 표에서 보듯이 4가지 경우 모두 3개의 요소 케이블로 구성되어 있는데, 각 요소 케이블의 길이는 전체 길이의 1/3로 모두 동일하다. CASE 1의 중앙부분 요소 케이블(
[Table 2] Specific values of multi-component cable cases 1~4
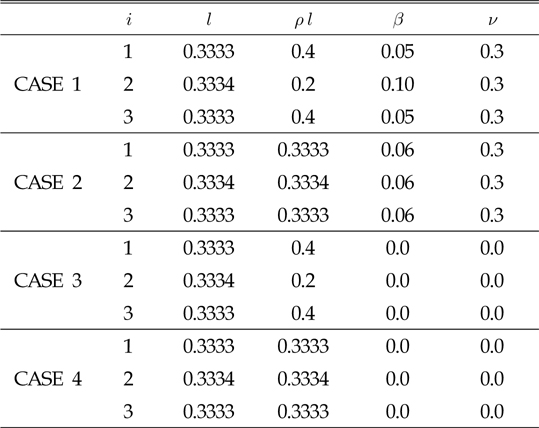
Specific values of multi-component cable cases 1~4
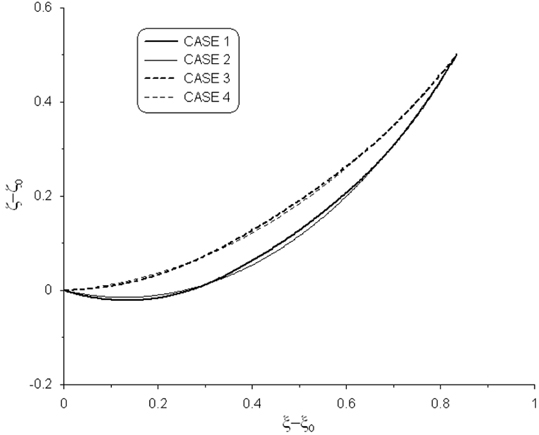
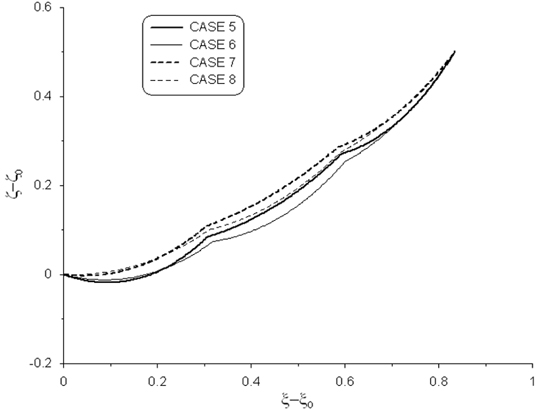
Fig. 2에 복합 케이블들의 형상을 도시하였다. 불균일한 케이블인 CASE 1 및 3과 균일한 케이블인 CASE 2 및 4를 비교해 보면 무거운 요소 케이블 부분이 더 처지고 가벼운 부분은 덜처짐을 알 수 있다. 주어진
집중하중에 의한 영향을 살펴보기 위해 CASE 1~4의 절점들에 복합 케이블 자중의 20%에 해당하는 수직 상방 하중
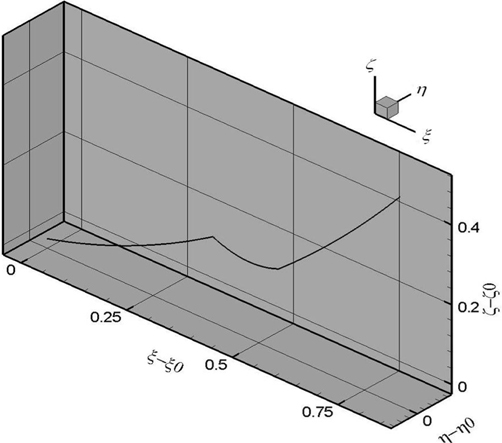
3차원 집중하중에 대한 해석 예로써 Table 2의 CASE 1에 와 이 작용하였을 때의 3차원 형상을 Fig. 6에 도시하였다. 이때 양 끝단 조건은
물성이 다른 요소 케이블들로 구성된 복합 케이블에 3차원 정적 집중하중이 작용하였을 때의 해석법을 개발하였다. 인장 변형을 고려한 요소 케이블에 대한 해석적 해 들을 바탕으로 절점 작용하중과 장력과의 힘의 평형조건을 사용하여 복합 케이블의 해석적 해를 케이블 시작점에서의 세 개의 미지 값으로 표현하였다. 이러한 미지 값들은 경계조건인 복합 케이블 양 끝단 위치조건에 의해 결정된다. 이 값들을 사용하면 복합 케이블의 형상, 장력 분포, 인장 변형, 케이블 단면적 변형비 등을 해석적으로 구할 수 있다.
해석 예로써 2차원 평면에서 수직방향 집중하중이 작용하는 경우에 대하여 해석 하였고 균일 케이블에 대한 결과와 비교하였다. 그리고 3차원 집중하중에 대한 해석 예도 제시하였다.
본 연구결과를 수중 복합 케이블에 적용하기 위해서는 케이블들의 자중을 수중 부력을 고려한 수중에서의 자중으로 대치 하면 되며, 이 때 구해지는 장력은 유효 장력(Effective tension)으로 해석하면 된다.