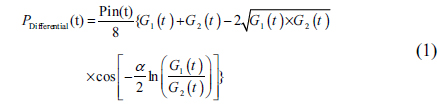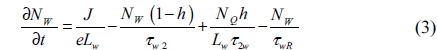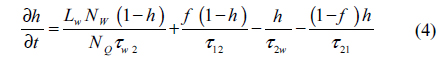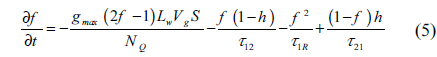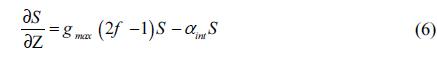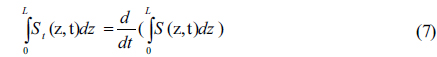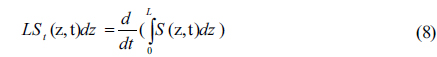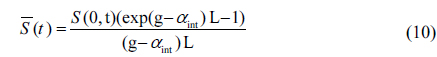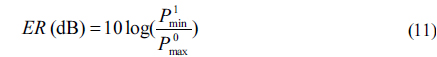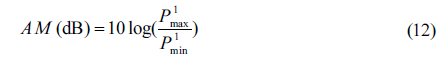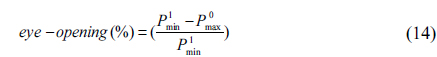All-optical gates will be essential elements in future communications systems. All-optical processing has many applications, such as wavelength conversation, add-drop multiplexing, regeneration clock recovery, simple bit-pattern recognition, address recognition, signal processing, and packet synchronization [1-3]. Subtraction is one of the most important operations in Boolean functions and is used in binary subtraction, binary counting, arithmetic logic units, encryption, and decryption in security networks. Many designs for a single subtractor or subtractor with adder have been proposed by using a semiconductor optical amplifier (SOA) and periodically-poled lithium niobate (PPLN) waveguide [4], micro-ring resonator [5], exploiting four-wave mixing (FWM) in a SOA [6], a SOA based-Mach-Zehnder interferometer (MZI) [7], a three-state system [8], a terahertz optical asymmetric demultiplexer (TOAD) [9], a single-slot waveguide [10], two SOAs [11], implementing nonlinear material [12], and a nonlinear directional coupler [13]. SOA with quantum-dot active region is a promising candidate for ultrafast operations [14-15]. The high output power, low threshold current density, ultra-fast response behavior, good temperature stability, and low noise level of the quantum-dot SOA (QD-SOA) have been demonstrated, and it has been emphasized that these elements can be utilized as building blocks of alloptical systems [17-19]. In this paper, using two QD-SOA MZI, we design a subtractor that can operate and perform well at speeds of over 250 Gb/s.

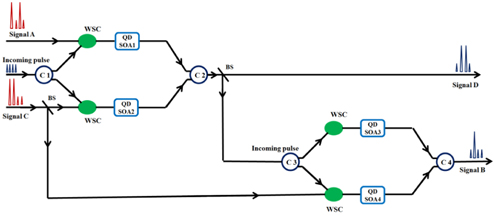
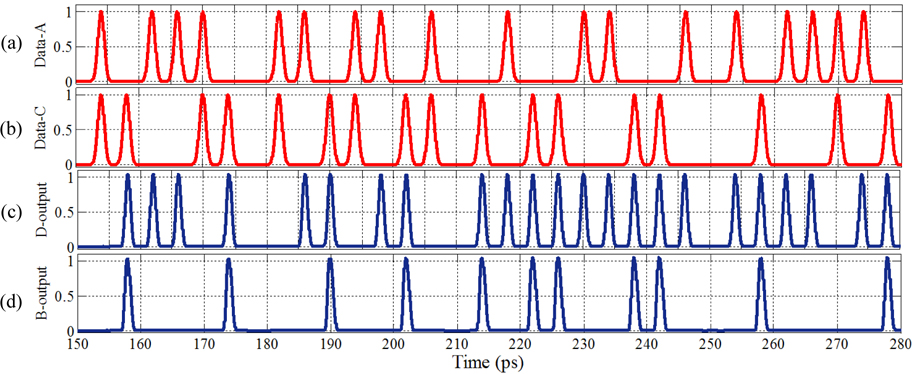
The subtractor is a combinational logic device that performs subtraction between two binary numbers. Its A and C inputs are for the minuend and subtrahend respectively. The differential and borrow outputs are D and B respectively. If A and C are equal then B=D=0, but if A=1 and C=0 then the outputs will be D=1, B=0. If A=0 and C=1 the outputs will be D=1 and B=1. Figure 1 shows the structure of our proposed subtractor. In the first MZI a differential bit is generated for which XOR operation has been done between A and C. Next the borrow bit is generated in the second MZI in which the differential bit acts as a probe signal. The theoretical results were verified by numerical simulation.

The output powers of the gate are expressed as,

where Pin (t) denotes probe power that is a continuous wave pulse, G_1,2,3,4(t) are the instantaneous gains of QD −SOA_1,2,3,4 respectively, and α is the QD-SOA linewidth enhancement factor. To calculate gain and power we must solve the three-level rate equation for the electron transmission between the wetting layer (WL), exited state (ES), and ground state (GS) respectively, which are as follows [20-22].

and the photon rate equation is

where z is the longitudinal direction along the QD-SOA length L, t is the local time, and V_g≈ 8.3× 10⁷m/s, S (z, t)= P (z, t) /(A_eff V_g hν) is the photon density of the input data signal. g_max is maximum modal gain, α_int is material absorption coefficient, hν is the photon energy, J is the injection current density, e is electron charge, N_W is the electron density in WL, and h and f are the electron occupation probabilities in the ES and GS respectively. N_Q is the surface density of QDs, L_W is the effective thickness of the active layer, 𝜏_2w is the electron escape time from the ES to the WL, 𝜏_WR is the spontaneous radiative life time in WL, 𝜏₂₁ is the electron relaxation time from the GS to the ES, and 𝜏_1R is the spontaneous relaxation life time in the QDs.

In order to investigate the feasibility of the proposed design, we have applied the 4th-order Runge-Kutta method to solve equations (3-5) numerically and to calculate the gain coefficient. The input pulses are pseudo-random binary sequences at 250 Gb/s whose profile is Gaussian, that is where P_max is peak power and T_FWHM is their full width at half maximum and less than 1.5 ps. By using Leibniz’s integral rule, we can interchange the integral and partial differential operators. By employing Leibniz’s rule for S (z, t), we have

and by integrating along the z variable in equation (7) we have

The next integration along the t variable in equation (8) gives

where (t) is the average of S (z, t) along the t variable. By integrating and normalizing [0, z], and solving for the optical power at location z in terms of the input power for S (z, t) in equation (6), and using equation (9), we have:

where g = g_max(2f −1) . In addition, the gain is calculated from . The simulation results and their comparison to the results of other papers verify this method. It was found that our method can solve rate equations more quickly than previous methods [18, 19]. The extinction ratio of the input signals was assumed to be 10 dB. The parameter values were taken from the literature on other QD-SOA-based interferometric gates [19-22]. These are: g_max = 14cm^-1, N_Q = 5× 10¹⁰cm⁻², 𝜏_W2 = 3ps, 𝜏_W = 1_ns, L_W = 0.25μm, 𝜏21 = 0.16ps, 𝜏_1R = 0.4ns, 𝜏₁₂ = 1.2ps, L = 4mm, P_max = 10dBm, α = 2 and J = 2.5kA / cm² . In order to assess the performance of an optical logic design, the most important parameters are extinction ratio, amplitude modulation, quality factor, pseudo-eye diagram, and relative eye opening, which we will investigate. The extinction ratio (ER) is defined as

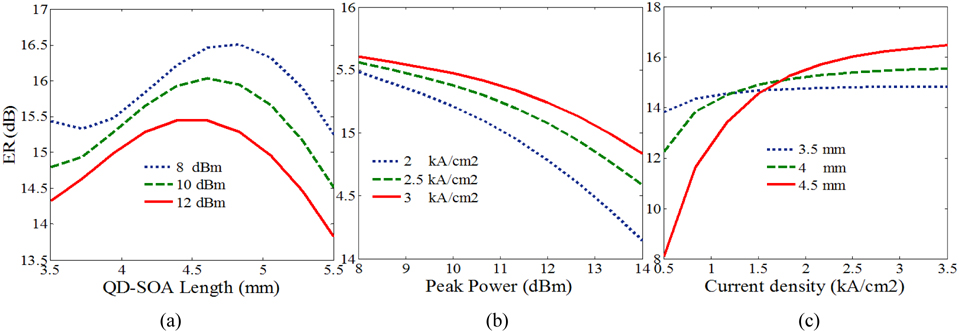
where and are the minimum and maximum values of the peak power of “1” and “0”, respectively [23]. In order to distinguish 1 unambiguously from 0 the ER must be over 10 dB [23]. Figure 2(a) depicts the ER variation versus QD-SOA length for three different peak power values of input data signals, where the other parameters are kept fixed. It is observed in the curves that for 4 <L <5mm, ER >14.5dB will result. The maximum values are shifted to the right as the QD-SOA length becomes larger. The smaller QD-SOA lengths need stronger control signals. Figure 2(b) shows the variation of ER with peak power for three different current densities. This shows that ER decreases with increasing peak power and increases with larger current density. Figure 2(c) shows the ER variation with current density for three different QD-SOA lengths. For J > 2kA / cm² we have ER >16dB because at higher injected current density there are more carriers in the wetting layer, and we have a better response.

The ratio between maximum and minimum peak power for signals corresponding to “1” is defined as

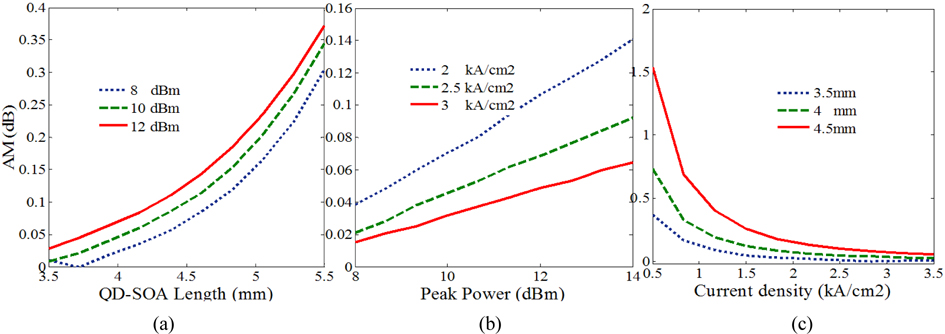
where and is the maximum peak power of “1” and “1” respectively [24]. The lower the AM, the more uniform is the level of the “1” outputs, and the smaller is the related pattern effect. Figure 3(a) illustrates the effect of QD-SOA length on the AM for three different peak powers of input data signals. For L < 4mm a very small AM is obtained, which is very desirable, and AM increases with larger peak powers. In Fig. 3(b) variations of AM with peak power for three different current densities are shown. The peak power increase has an undesirable effect on AM, while the increase of current density has a desirable effect on it. Figure 3(c) shows the variation of AM with J for three different QD-SOA lengths. It is observed that for J > 2kA / cm² we can achieve a small AM, and that AM increases with increasing of length.

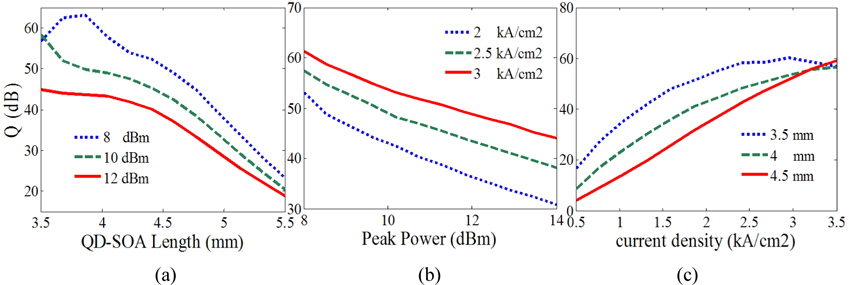
The quality factor is defined as

where m₁ (m₀) and σ₁ (σ₀) are the average power and standard deviation of the circuit output at “1” (“0”) respectively [25]. Figure 4 shows that Q decreases for L > 4.5mm and a larger peak power results from the decrease in Q factor. The results show that with J > 2.5kA / cm² and L = 4mm we can achieve a larger Q.

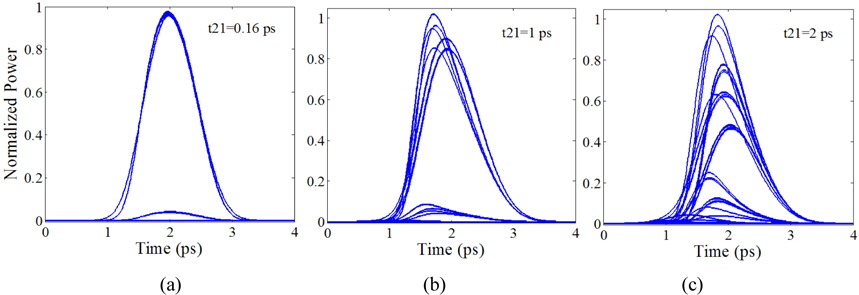
A pseudo-eye diagram is one of the best standards for assessing the output signals. A clear and open eye diagram is desired. Figure 5 illustrates the effect of electron relaxation time from ES to GS on PED. A slow transition of the electron between ES and WL results in a slower cross gain modulation. Thus speed is limited by the relaxation time from the wetting layer to the quantum-dot state.

The relative eye opening is defined as

where and are the minimum and maximum powers for ones and zeros respectively [10]. In this design the related eye opening is over 90%. Table 1 shows the relative eye opening for three QD-SOA lengths and three electron relaxation times from ES to GS. The other parameters are kept fixed.

According to Figs. 2-5 and our discussions so far, QDSOAs with lengths smaller than 4.5 mm, show desirable responses but smaller lengths decrease unsaturated gain. Table 2 shows gain values for five different QD-SOA lengths. It was found that with current density of more than 2.5kA / cm² we can achieve a more suitable performance. Increasing the current density might not be practical for a QD-SOA [22], however, and we see that with smaller peak power the output is better, so for good switching we choose a peak power of 10 dB.

According to the above mentioned explanations and using the combination of input parameters L = 4mm,J 2.5kA / cm², P_max=10dBm and 𝜏₂₁ = 0.16ps, we can achieve these values in the output: ER = 15.37 dB, AM = 0.052 dB, eye-opening = 97.09%, Q = 49.13 dB, and 20.82 dB of unsaturated gain for 250 Gb/s input signals. Figure 6 shows input and output data streams for a 32-bit pseudorandom binary sequence of input.

Table 3 illustrates the output parameters of the proposed structure, compared to those of similar recent structures. The last column shows the parameters of our designed structure, which demonstrates its better performance, due to our choice of optimal parameters for the structure, and use of the transmitting ports in both MZIs.

The main reason for the faster response of a QD-SOA compared to a bulk SOA is the presence of the wetting layer. The wetting layer serves as a carrier reservoir: Carriers depleted by the injected optical pulse in the QD ground state are replaced from the wetting layer by fast carrier transfer. At a higher injected current density there are more carriers in the wetting layer, resulting in a better performance. Thus the speed of optical logic gates is limited by the carrier recovery time in the device. Careful adjustment of the peak power of the modulated signal and QD-SOA bias current is necessary for error-free performance at high data rates and for avoiding overlap in response.

The effects of the most important parameters on the performance of the proposed gate are investigated using a model of three coupled equations for a QD-SOA into which a Gaussian pulse with rate 250 Gb/s has been inserted. The results show that output signals have high ER and Q and low AM, and that the gate can operate well at speeds of over 250 Gb/s. In both MZIs we used the transmitting port. The reflecting port can also be used to extend the device in generating other logic gates.