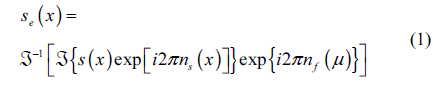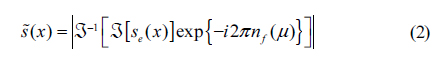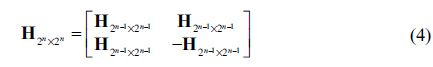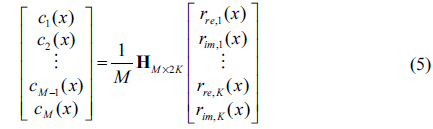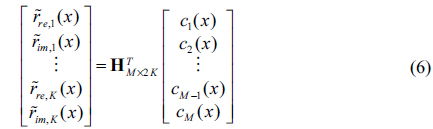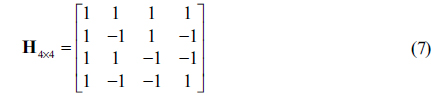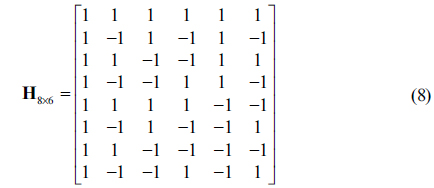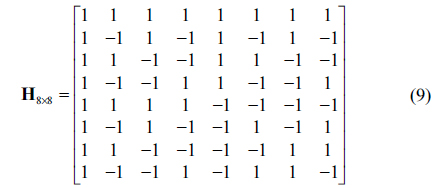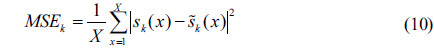In this paper we extend double random phase encryption (DRPE) using orthogonal encoding from single-image transmission to multiple-image transmission. The orthogonal encoding for multiple images employs a larger Hadamard matrix than that for a single image, which can improve security. We provide a scheme for DRPE with an orthogonal codec, and a method for orthogonal encoding/decoding for multiple-image transmission. Finally, simulation results verify that the DRPE using orthogonal encoding for multiple images is more secure than both the conventional DRPE and the DRPE using orthogonal encoding for a single image.
A significant issue in transmitting private or confidential information is information security. Encryption techniques for secure data transmission have been well developed [1-26], and lots of research has focused on optical encryption [3-26]. One widely used optical technique is double random phase encryption (DRPE) [3]. It provides high encryption speed, but requires updating of the key phase masks [4]. To improve the security of DRPE, fractional Fourier transform has been adopted in DRPE systems [25], but it requires much more information in the keys for encryption and decryption. An increase in the key information can make the DRPE systems more complicated, so DRPE using orthogonal encoding has been proposed for single-image transmission [26]. The orthogonal encoding technique for single-image transmission employs only simple, linear operations based on the Hadamard matrix of order 2 with the orthogonality property [27]. Thus, the use of orthogonal encoding can enhance the security of DRPE at the cost of a little complexity.
In this paper we extend DRPE using orthogonal encoding from single-image to multiple-image transmission. The orthogonal encoding for multiple images uses a larger Hadamard matrix than that for a single image, and hence is more secure. We provide a scheme for DRPE with an orthogonal codec for multiple-image transmission. Furthermore, we show simulation results verifying that the multiple images encrypted by DRPE using orthogonal encoding are not correctly decrypted even when the key information used in DRPE is known.
The paper is organized as follows. Section II presents the basic concept of DRPE. Then, DRPE using orthogonal encoding for multiple-image transmission is described in Section III. To verify this optical encryption method, simulation results produced by DRPE using orthogonal encoding are provided in Section IV. Finally, we conclude with a summary.
II. DOUBLE RANDOM PHASE ENCRYPTION TECHNIQUE
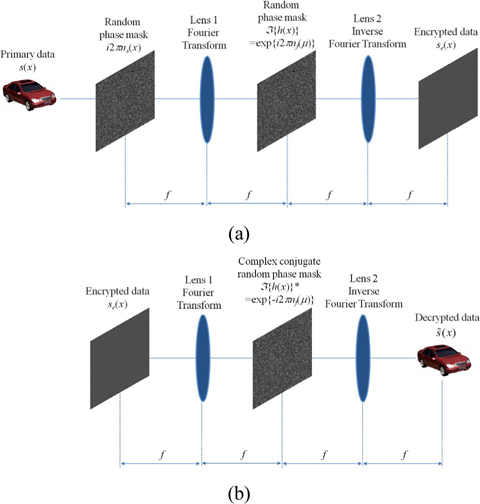
DRPE, an optical encryption technique, can provide high encryption and decryption speed. In addition, it can be implemented simply. It uses two random phase noises (i.e., random phase masks) for the encryption process. Then, noise like encrypted data can be obtained. For decryption, the key random phase mask is convolved with the encrypted data. To understand the DRPE concept, we consider only one-dimensional data. Let us assume that the primary data is
where ℑ-1 indicates the inverse Fourier transform. This encrypted data can be separated into amplitude and phase, i.e.
For decryption, the complex conjugate of the key information (i.e. the Fourier transform of
III. DOUBLE RANDOM PHASE ENCRYPTION USING ORTHOGONAL ENCODING
3.1. Procedure for DRPE using Orthogonal Encoding
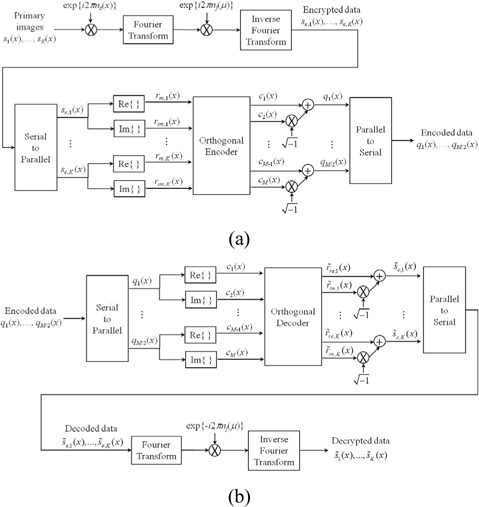
In this paper we assume that
As shown in Fig. 2(b), to correctly decrypt the orthogonally encoded data, first the encoded data are converted from serial format to parallel format and decomposed into real and imaginary components. Then the real encoded data are decoded with the orthogonal matrix used in the encoder. From the real decoded data (
3.2. Orthogonal Encoding and Decoding Technique
For orthogonal encoding and decoding of multiple images, we use the Hadamard matrix of order 2
where
where 2=[1 1; 1 -1]. On the other hand, when 2
By using the Hadamard matrix in the orthogonal encoder, the real and imaginary components of the encrypted data for
where ,
In the orthogonal decoder, the real and imaginary com- ponents of the encoded data
where (
The orthogonal encoder and decoder consist of only simple linear operations, as described in Eqs. (4)-(6). Hence, the addition of the orthogonal encoder and decoder to the DRPE system does not require any high cost or effort.
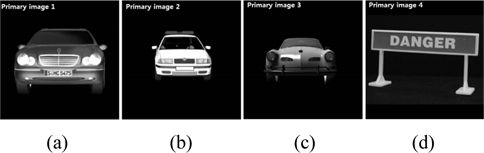
For performance evaluation of DRPE using orthogonal encoding, we use four primary images with 500 (H)×500 (V) pixels as shown in Fig. 3. We consider transmissions of two, three, and four images. For two-, three-, and fourimage transmissions the primary images in Figs. 3(a) and 3(b), Figs. 3(a)-3(c), and Figs. 3(a)-3(d) are used respectively, and the following Hadamard matrices are used respectively.
Figures 4-6 show the encrypted and encoded images for two-, three-, and four-image transmissions respectively. These figures indicate that the images encrypted by DRPE and encoded by orthogonal encoding are perfectly encrypted, and thus look like noise. It is noted that for three-image transmission, four encoded images are generated because the order of Hadamard matrix is eight. Figures 7-9 show
the decrypted images, with and without decoding, for two-, three-, and four-image transmissions respectively, when the key information of DRPE is perfectly known for decryption. In the case of no decoding, the complex encoded data are not decoded with the orthogonal decoder, but directly decrypted. Thus, (
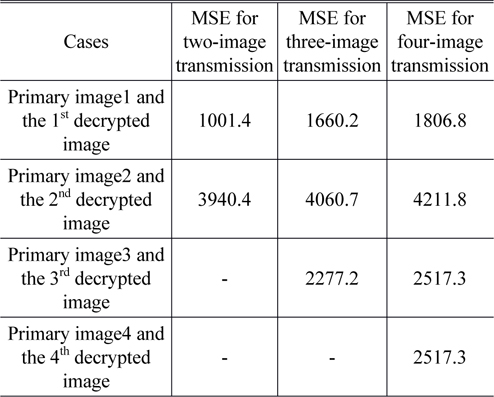
Figures 10(a)-10(i) show the decrypted images for two-, three-, and four-image transmissions respectively, when perfect key information of DRPE is used for decryption but the wrong decoding is employed. For the wrong decoding method we use the Hadamard matrix of order 2 that was adopted for decryption of the single-image transmission [26]. For encoding of two-, three-, and four-image transmissions, we use the Hadamard matrices of order 4, 8, and 8, res- pectively. Thus the Hadamard matrices used for encoding and decoding do not match. As seen in these figures, the decrypted images somewhat include the primary images, but overlapped, and image recognition becomes worse as the number of transmitted images increases, i.e. the size of the Hadamard matrix increases.
[TABLE 1.] MSE results of DRPE using orthogonal encoding when incorrect decoding is used
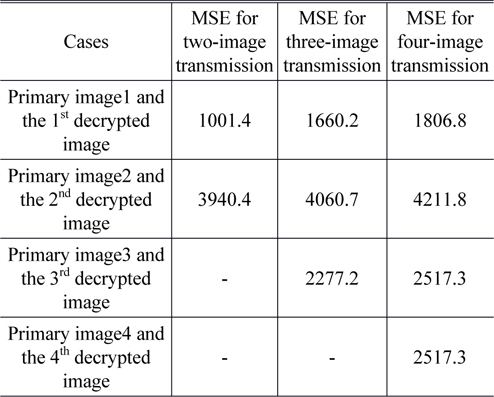
MSE results of DRPE using orthogonal encoding when incorrect decoding is used
To quantify the difference between the primary images in Figs. 3(a)-3(d) and the decrypted images with incorrect decoding in Figs. 10(a)-10(i) respectively, the mean square error (MSE) is evaluated. MSE between the
where
We present a DRPE technique using orthogonal encoding for multiple-image transmission. Particularly we provide a scheme for DRPE using orthogonal encoding for encryption and decryption as well as the method for orthogonal encoding and decoding with the Hadamard matrix. From simulation results we verify that DRPE using orthogonal encoding for multiple-image transmission is more powerful than that for the single-image transmission, in terms of security. Furthermore, since the orthogonal encoder and decoder consist of only simple linear operations, the DRPE system using orthogonal encoding for multiple-image transmission can be implemented with low cost and effort.