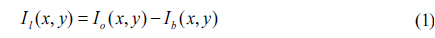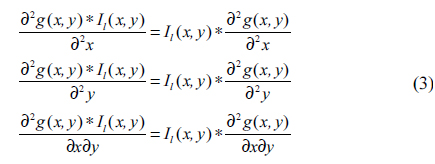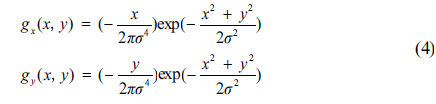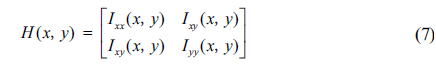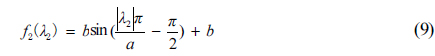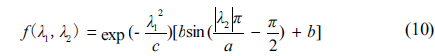Vision measurement of structured light is one of the important approaches for three-dimensional object measurement and has the advantages of bring noncontact and informative, with moderate measurement speed and measurement accuracy [1]. It is widely used in the inspection of automobile parts, the morphology testing of vehicle surfaces, medical CAD/CAM, quality assurance, and other metrology fields [2-6]. A measurement system for structured light generally consists of a camera, a laser projector, and a computer [7, 8]. The image from a laser line shining on the object is the source of information to achieve the measurement task. One of the key steps in the whole measurement task is to extract accurately the center positions of a laser line [9, 10]. The ideal center positions of a laser line should be a single-pixel-wide curve located in the center of the light line [11, 12]. As an actual light plane is produced with a certain thickness, the intersection curve of the light plane and measured object surface also has a certain width. Therefore, fast and accurate center extraction of a laser line in a test image is of great significance to the vision measurement system of structured light [13, 14].
Currently, extraction methods for the centers of a laser line can be classified into two categories. One category is based on pixel level, such as the extreme-value method [15, 16], threshold method [17-19], and directional-template method [20-22]; the other category is executed at the subpixel level, including the gray-centroid method [23, 24], curve fitting [25, 26], and the Hessian-matrix method [27-29].
The principle of the extreme-value method [15, 16] is to choose the pixel with maximum gray value on the transverse section of a laser line as the center of the laser line. This method achieves simple and fast extraction and gives better recognition results when the grayscale distribution of a light line obeys an ideal Gaussian distribution. Nonetheless, it is susceptible to noise. Noisy points in an image captured by a camera often remain in the image even after filtering. Therefore, in the actual measurement, when the grayscale distribution of a laser line is not strictly in accordance with a Gaussian distribution or is affected by noise, the recognized centers will deviate from the actual centers of laser line, leading to extraction results with lower accuracy. The threshold method [17-19] sets a boundary threshold to obtain two borders in the transverse section of a laser line, and the centers of the laser line are regarded as the centers of the two borders. The characteristics of this method are similar to those of the extreme-value method, which allows high processing speed. However, recognition errors are brought about when the grayscales of the transverse section in a laser line are distributed asymmetrically or affected by noise. In addition, it is also a complex issue to select a reasonable threshold. Useful pixels are missed if the threshold is too high, while useless pixels are generated if the threshold is too low. As the threshold interferes with the results of this method, the threshold method is often used with other methods as the first step to select the centers of the laser line. The directional-template method [20-22] sequentially convolutes the 0°, 90°, and 45° directional templates with the image containing a laser line. By this method, extreme points in the transverse section of the laser line are strengthened after convolution, while the other surrounding points are suppressed correspondingly. If the direction of the laser line is identical to the template orientation, the locations of the extreme points will be more prominent. Comparing the process results of each directional template, the point with maximum value is the section center of the laser line. The directional-template method improves the former approaches by repairing disconnected lines and noise suppression. However, this method increases the amount of computation and data storage needed, since each line in the image should be convoluted with the templates in four directions. Overall, the methods above extract the centers of the laser line at the one-pixel level of precision. To enhance the measurement accuracy of the structured light method, researchers further proposed several extraction methods at the sub-pixel level. The gray-centroid method [23, 24] directly calculates the grayscale center along the abscissa as the center position according to the arrangement of gray values of a laser line in a certain range. First, the maximum grayscale point of the laser line is found by the extreme-value method above; then several pixels are chosen around this maximum point. The center position of the laser line in this region is determined by the centroid equation. The gray-centroid method investigates the light intensities of all the points around the extreme point, avoiding the negative impacts of uneven light distribution on the extraction results. Nevertheless, as this method searches for the maximum grayscale point of the laser line by applying the extreme-value method, it is also very sensitive to noises, as is the extreme-value method. Since the gray-centroid method performs line scanning, the extraction accuracy is affected by the curvature of the laser line, so this method is generally used for a laser line with little curvature. The curve-fitting method [25, 26] outlines the grayscale distribution of a transverse section of a laser line employing a Gaussian curve or a parabola. The center point of the transverse section is the local maximum of the fitted curve. This method is only valid for a wide laser line with constant direction of its normal vectors. Additionally, the actual grayscale distribution of pixels in a laser line is not strictly symmetrical, so the extreme point found via the curve-fitting process often deviates from the actual center of the laser line. The Hessian-matrix method [27-29] determines the centers of a laser line by analyzing the Hessian-matrix eigenvalues of the candidate feature points in the laser line. First, the centers of the laser line are distinguished by the features of the two eigenvalues of the Hessian matrix. The normal vector direction of the laser line is derived from the eigenvector corresponding to the eigenvalue of the Hessian matrix. After that, the subpixel center coordinate of the laser line is computed by implementing a Taylor expansion in the normal-vector direction. The Hessian-matrix method shows strong noise immunity, accurate extraction, and good robustness. It has obvious advantages under conditions of a complex environment and a high precision requirement. However, the thresholds of the eigenvalues in different transverse sections of a laser line vary over a wide interval, which causes the method to extract several redundant centers, or to miss the centers on the same transverse section of a laser line in the image. Seeking a method to acquire the centers of a laser line with adaptability and accuracy, a normalization model is presented to balance the judgment effects of two Hessian-matrix eigenvalues, which promotes adaptability under various conditions. Moreover, Taylor expansion is also exploited to enhance the extraction accuracy for a laser line at the subpixel level.
II. HESSIAN MATRIX METHOD FOR LASER LINE EXTRACTION
As the background also appears in the image, the image should be preprocessed to differentiate the detected laser line from the background, to reduce the amount of computation needed for recognizing the laser line. For this reason, the difference method shown in equation (1) is performed to segment a laser line from the original image [30].
where
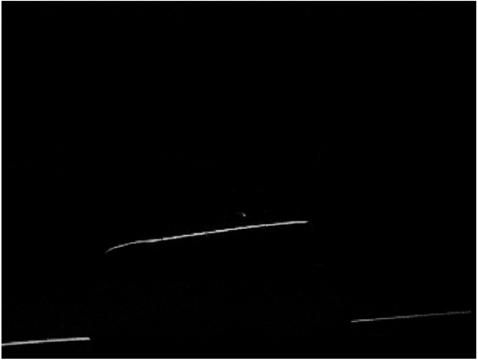
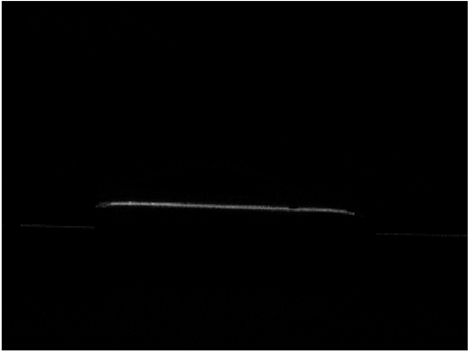
Figures 1(a) and 2(a) illustrate the target images comprised of the background with an automobile model and a laser line projected onto the surface of the automobile. Figures 1(b) and 2(b) show the backgrounds without the laser lines. The background image is subtracted from the target image to obtain the laser line from the image variation, as shown in Figs. 3 and 4. After image preprocessing, this method removes the irrelevant information such as background, preserves the interesting area with the laser line, and reduces the computation for laser recognition and promotes extraction speed in further steps.
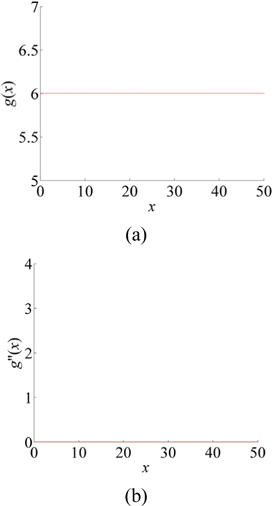
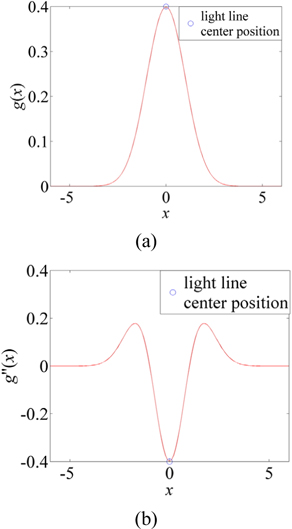
The Hessian-matrix method was proposed by Steger to extract line centers with good stability [28]. It is composed of second-order partial derivatives of the distribution function of the pixel grayscale values in an image, which expresses the concavity or convexity of the image. Since the crossing line of the laser plane and object surface, which is the laser line, obeys a Gaussian distribution in its transverse section, the second-order partial derivatives of the pixels in different directions should be analyzed to investigate the grayscale distribution characteristics of the laser line in an image [27]. Figure 5(a) explains the variation tendency of gray values along the axis direction of an ideal laser line in an image. Because the variation of gray values is quite small, the partial derivative is approximately regarded as zero, as is interpreted in Fig. 5(b). The variation tendency of gray values along the direction perpendicular to the laser line follows a Gaussian distribution, as shown in Fig. 6(a). The second derivatives of the Gaussian function along the direction perpendicular to the laser line axis are generated to obtain the characteristic of second derivatives of the gray values in this direction, as shown in Fig. 6(b). The second-derivative value related to the center position of the laser line in the transverse section is far less than zero. In conclusion, the rules to determine centers of a laser line are these: The second-order partial derivatives along the central axis of the laser line approach zero, while the second-order partial derivatives along the direction perpendicular to the laser line axis are far less than zero. In other words, the grayscale distribution along the central axis of the laser line is approximately constant, while the grayscale distribution along the direction perpendicular to the laser line axis is a convex function.
Two eigenvalues of the Hessian matrix respectively express the function's convexity along two orthogonal eigenvectors for any pixel in the image, so the center positions of the laser line can be decided by the characteristics of the two eigenvalues of Hessian matrix. The direction of the laser line is also estimated by the two eigenvectors [31].
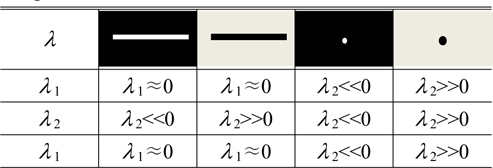
Table 1 summarizes the relationships between the eigenvalues of the Hessian matrix and the typical grayscale distributions in an image [32]. Whether a pixel is the center of a laser line in an image can be decided if one eigenvalue of the Hessian matrix is close to zero and the other eigenvalue is far less than zero. Obviously, decision rules for other features in Table 1 can be deduced from the above analysis for a laser line.
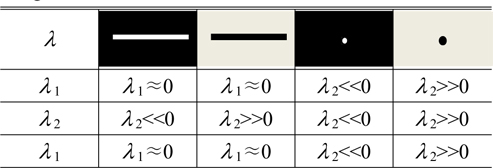
Relationships between the eigenvalues λ 1 and λ 2 of the Hessian matrix and typical grayscale distributions in an image
As there is noise in the image, the image
The Gaussian filter is expressed by
According to the differential theorem, the convolution results of image
From Eq. (3), the second-order partial derivatives of the Gaussian function should be calculated first, then the second-order partial derivatives convoluted with the image
The first-order partial derivatives of the Gaussian function are expressed by
The second-order partial derivatives of the Gaussian function are denoted by
Based on Eqs. (4) and (5), the convolution results of the original image and the first-order and second-order derivatives are clarified by Eq. (6) to filter noise in the image.
where
According to Eq. (6), the Hessian Matrix of an arbitrary pixel in an image is given by
Suppose
With this method, two thresholds should be selected to determine the ranges of the two eigenvalues of the Hessian matrix. Too high a threshold leads to losing some center pixels in a laser line, whereas too low a threshold results in more than one center produced in one transverse section of a laser line. To solve this problem, a method for extracting laser line centers is proposed based on a standardized model with a sinusoidal function and a Gaussian fuction. The center positions of a laser line are found by this method.
III. NORMALIZATION MODEL OF LASER LINE EXTRACTION
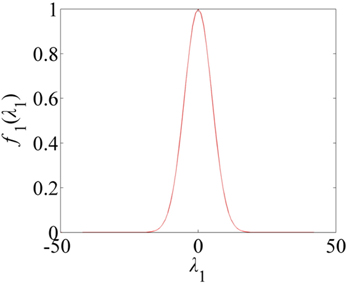
To determine reasonable thresholds for the eigenvalues, a normalization model combining a sinusoidal function and a Gaussian fuction is constructed to extract the laser line centers. First, according to the two eigenvalues of the Hessian matrix, an initial lower threshold is set to choose the preliminary feature points of laser line centers. A lower threshold relatively avoids discontinuous points and completely retains feature pixels of laser line centers. Then, since the gray values are basically constants in the small regions along the axis direction of the laser line, the eigenvalue
where
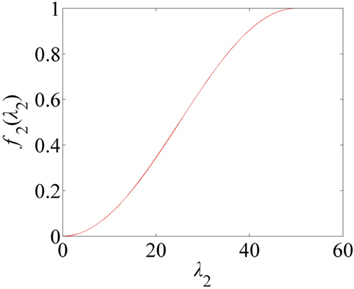
As the gray values in the direction perpendicular to the central axis of the laser line follows a Gaussian distribution, the eigenvalue
where
In light of Eqs. (8) and (9), the decision function of the laser line centers based on a sinusoidal function and a Gaussian fuction is given by
where
where
As elucidated in Fig. 8, the variance ratio of the sinusoidal function increases slowly at both ends but increases quickly in the middle. The benefit is that the resulting distinction is more obvious after the eigenvalues of the different feature points have been substituted into the sinusoidal function. The normalized function provides enormous discrimination between the central and noncentral points.
In this section, a normalization model integrating a Gaussian recognition function and a sinusoidal recognition function is proposed, to balance the estimation effects on the initiatory laser line centers. The final selected centers are decided by the proposed function, which implies the distribution characteristics of the grayscales along the central axis direction and perpendicular to the central axis direction of the laser line in an image.
IV. SUBPIXEL EXTRACTION OF LASER LINE CENTERS
To enhance the accuracy of extraction of the center coordinates of a laser line, the subpixel coordinates of the centers need to be calculated after the pixel coordinates of the laser line have been acquired as in the above sections. As the intensity distribution of the laser line in the transverse section follows a Gaussian distribution, the subpixel coordinates of the laser line centers should be located along the normal direction of the pixel coordinates. In the normal direction, the minimum point of the second-order derivative of the image is the subpixel center of the laser line. Because the direction normal to the laser line is the eigenvector direction corresponding to the minimal eigenvalue of the Hessian matrix, the subpixel coordinates of the laser line centers can be estimated along the normal direction of the central points. In terms of eigenvalues of the Hessian matrix associated with the pixel coordinates of laser line centers, the eigenvector direction related to the minimal eigenvalue, which is the direction normal to the laser line center, can be found. Let (
where (
As the subpixel point is located on the inflection point in the normal direction, the first-order partial derivative of Eq. (12) is calculated and then set equal to zero [27].
where
V. EXPERIMENTAL RESULTS AND DISCUSSIONS
A vision measurement system of structured light is built to prove the feasibility and accuracy of the outlined standardization model for extracting laser line centers. Experiments on extraction effects of the laser line centers are performed. The experimental system mainly consists of a laser projector, a camera, two tripods, and a computer, as described in Fig. 10. A laser projector with a red laser is used to generate a line on the object's surface. The wavelength of the laser is 635 nm. The camera is DH-HV3102UC-T with the Computar® lens, whose focal length is 5 mm. The image resolution is 640×480. The computer configuration is two 1.6 GHz CPUs and 2 GB of memory.
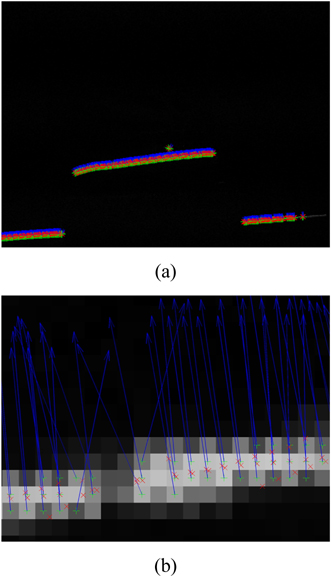
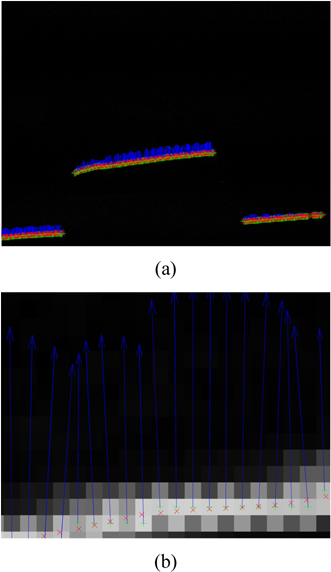
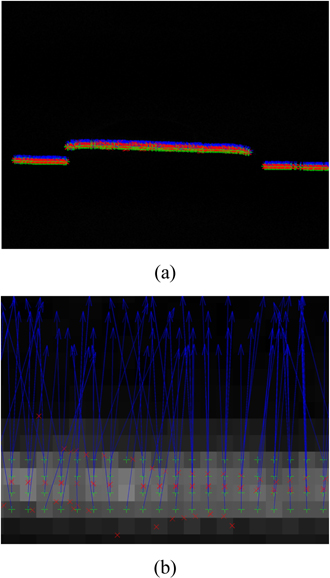
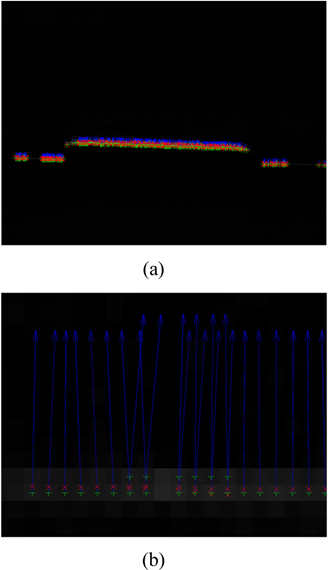
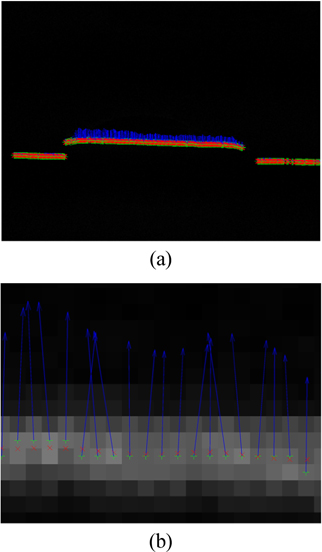
The difference method is executed to preprocess the first group of images in Fig. 1. The image containing the laser line is shown in Fig. 3. The recognition result and amplified image of the laser line centers extracted by the traditional Hessian matrix method are shown in Fig. 11. The arrows represent the eigenvector directions at the centers perpendicular to the laser line axis. “+” denotes the pixel coordinates of light line centers. “×” denotes the subpixel coordinates of the laser line centers after subpixel analysis. The thresholds are 8 and −8 in Fig. 11. It limits the laser line centers with the conditions that the absolute value of the near−0 eigenvalue λ1 should be smaller than 8, and the eigenvalue
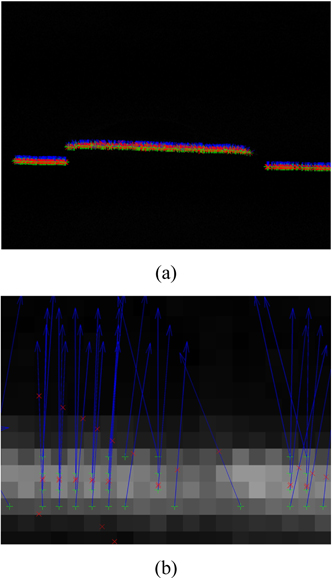
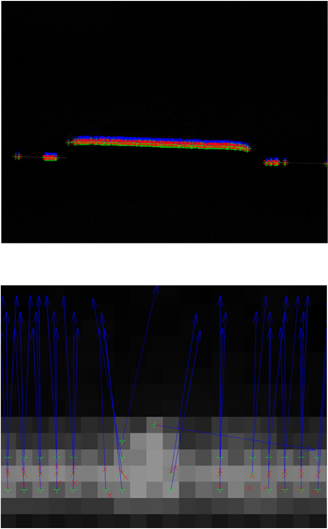
To improve the extraction stability of laser line centers in active vision, an extraction method for laser line centers based on a standardized model with a sinusoidal function and a Gaussian function is presented. First, preprocessing of the camera-captured image with a difference method is conducted to segment the laser line from the complex background image. Then the eigenvalues and eigenvectors of the Hessian matrix are calculated after obtaining the Hessian matrix of each pixel on the laser line. Thresholds are acquired according to the characteristics of the Hessian matrix eigenvalues of laser line centers that follow a Gaussian distribution, which is used to select the initial laser line centers. Third, combining the characteristics of a sinusoidal recognition function and a Gaussian recognition function, a standardized model of eigenvalues for the Hessian matrix is constructed to extract laser line centers accurately. In the proposed model the sinusoidal recognition function corresponds to the Gaussian distribution of the laser line in transverse section and assigns a larger weight to the real center that has a negative eigenvalue with a large absolute value. The Gaussian recognition function explains the constant distribution of the laser line in longitudinal section and gives a larger weight to the center with eigenvalue close to zero. The advantage of this model for constructing a normalized decision function is to identify the real centers from the candidate centers. In the decision function of the model, if one eigenvalue of the Hessian matrix at the pixel point is close to 0 and the other one is much less than 0, the normalized result is near 1. In other conditions, the standardized result approaches 0. Therefore, the former decision basis which depends on the eigenvalues is legitimately standardized to the interval between 0 and 1 by the decision function, which supplies a unitary decision value to improve the recognition rate of the laser line centers in different images. Finally, a comparative experiment is completed with the traditional method. The experiments put the two eigenvalues of the Hessian matrix into the standardized model. The maximum points of standardization results in each column are adopted as laser line centers. The foundation that balances the two eigenvalues of Hessian matrix is presented for the process of determining the laser line centers. The subpixel level results of center coordinates of the laser line are found. For 100 continuous centers of a laser line in two group images, the proposed method increases the recognition rate of two image groups from 60% to 86% and from 51% to 89% compared to the former method. The experimental results show that the normalization method that integrates the Gaussian and sinusoidal recognition functions elucidates the distribution characteristic of laser line centers and improves the extraction accuracy for the coordinates of laser line centers.