In order to enhance the performance of an apodized optical system, we need to bring about changes in the pupil function with a relevant apodization technique. Apodization is a technique used for modifying the amplitude impulse response of an optical imaging system. Studies involving apodization have gained importance in real-time imaging experiments for various purposes [1-6]. In most of the earlier studies [1-6] on apodization, the amplitude point spread function (PSF) was perfectly symmetric in nature on both sides of the diffraction head. In 1991, Cheng and Siu [7] introduced asymmetric apodization and succeeded in achieving suppressed sidelobes and a steep central peak on one side, the so-called ‘good side,’ of the diffraction head at the cost of worsening its counterpart on the other side, the so-called ‘bad side,’ with enhanced sidelobes and a broader central peak. In a further extension of their work [8], they achieved enhanced sidelobe suppression and improved the performance of linear antenna arrays or optical gratings with asymmetric apodization [9]. Kowalczyk et al. [10] used this technique to achieve axial and lateral super-resolution in confocal scanning systems, and Granieri et al. [11] applied the same technique to an analysis using fast Fourier transform (FFT) and investigated the focusing properties of an apodized pupil function. Andres et al. [12] clearly observed the off-axis focal shift for rotationally nonsymmetric screen functions. Further, for high-reflectivity linearly chirped fiber gratings, a significant improvement in suppressing the sidelobes and smoothing the curves has been achieved by employing the asymmetric apodization technique [13]. Chollet and Goedgebuer [14] presented the experimental preparation of a LiNbO3 composed optical filter used for reducing sidelobes in the asymmetry mode. Kolpakov et al. [15] used the same technique to produce a dispersion-less Fabry–Perot fiber cavity with the use of a pair of fiber Bragg gratings. Applebuam and Chapman [16] developed a widely used technique in antenna arrays for sidelobe cancelling. It is well-known that through appropriate apodization in the exit pupil of an optical system, a PSF in the focal region may be shaped into the desired form, thereby increasing the resolving power of the instrument or optical system. This forms the basis of our investigation. We are further motivated by the work of Siu et al. [8, 9], who introduced the concept of asymmetric apodization for enhancing the resolving power of an optical system. From an in-depth analysis of the process of apodization, we have found that asymmetric apodization can result in better characteristics of the diffraction field, because it has a strong suppression effect on the sidelobes along with a sharp central peak on the good side. The work reported on asymmetric apodization suggested the idea to randomly distribute anti-phased weights to semicircular ring elements at edges, over the central circular region with uniform transmittance. We obtained some useful results by employing aperture functions in optical imaging systems for imaging point structures. A general asymmetric apodization across the pupil plane yielded significant improvement in the intensity distribution of the diffraction field. Thus, this technique has found applications in areas like optical imaging, spectroscopy, astronomy, and radar communication. In a previous paper [17], we reported the results obtained using the PSF of asymmetrically apodized optical systems with one-dimensional (1D) case-complex pupil filters. The present study generalizes this research to a 2D pupil function (semicircular arrays of the circular pupil). Following Siu et al. [9], we investigated the intensity PSF of a 2D aperture function (semicircular arrays of the circular aperture).
According to the simplified scalar wave-diffraction theory, the amplitude PSF of a 2D apodized optical system is the Fourier transform of the pupil function.
To implement asymmetric apodization, the array of aperture is modified as: certain number of new semicircular elements are added at the left-hand side with the amplitude of 1/
1) The diffraction field amplitude calculated using the circular aperture of radius (1 -
where sin
2) Complex amplitude calculated using the left semicircular array of discrete elements:
3) Complex amplitude calculated using the right semicircular array of discrete elements:
With the amplitude of each element normalized to 1/
Thus, the intensity PSF is
The results of investigations on the effect of discrete-type asymmetric apodization on the point spread function of an apodized optical imaging systems have been studied analytically from Eq. (5), as functions of the optical coordinate z varying from –12 to +12. An iterative method of numerical integration has been developed and applied to compute the positions and intensity values of the first minima (dark ring) and maxima on both sides of the detected pattern. Our focus is mainly on the positions and intensities of the central maxima, positions of the first minima, and intensities of the first optical sidelobe on the bad side of the diffraction field. These values are obtained for different conditions, and the higher-order sidelobes are neglected as they are suppressed to the zero level.
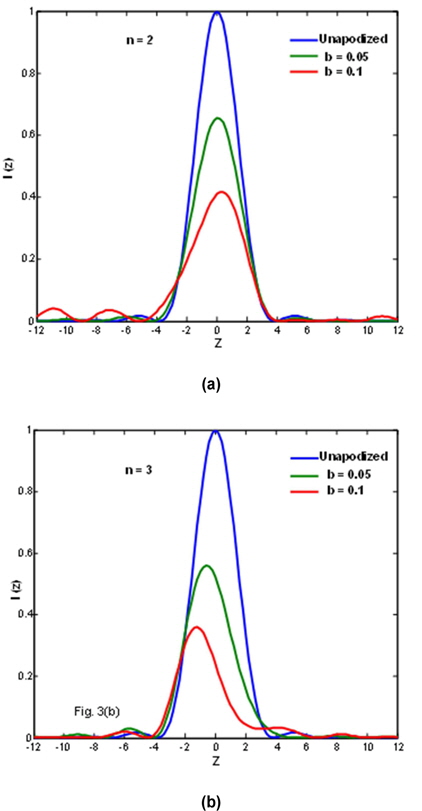
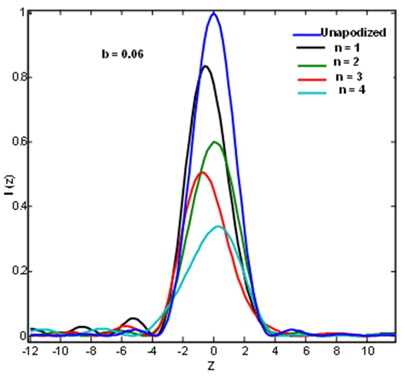
We describe the performance of a 2D array of semicircular discrete elements with asymmetric apodization in terms of these parameters since they are the parameters used for quantifying the resolution of apodized optical imaging systems. The efficiency of the designed aperture functions is evaluated by their asymmetric PSF and is depicted in Figs. 3 and 4. In all these figures, the unapodized or airy PSF is represented by a solid blue curve for comparison with the apodized PSF curves. The PSFs shown in Fig. 3(a) and (b) are obtained for n number of semicircular elements, where
This figure shows that the asymmetry in the image plane depends not only on the degree of asymmetric apodization at the edges of the central circular aperture but also on the number of elements in the array of the 2D aperture. The PSFs in this graph present an effect of an array of elements with discrete asymmetric apodization on the suppression of secondary optical sidelobes in the diffraction feet. In our investigation, we observed that in the presence of definite coded phase apodization for a semicircular array of discrete elements, the secondary maxima were eliminated to a large extent on the good side. Hence, it can be noted that the optimum values for the semicircular edge ring width
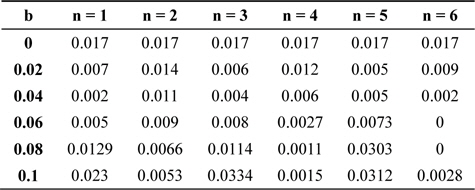
Table 1 shows the intensity of the first secondary maxima of the diffraction pattern for different values of the semicircular edge ring width
[Table 1.] First secondary maxima intensity on the good side
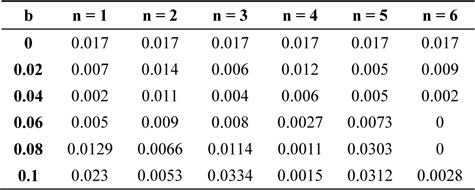
First secondary maxima intensity on the good side
This figure shows that for
For example, for
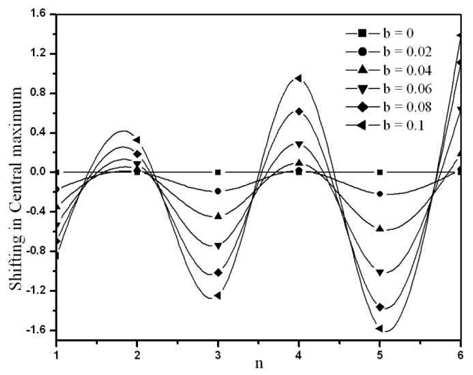
Fig. 5 clearly shows that the shift of the central maximum position towards the good side has a linear relation with the semicircular ring width
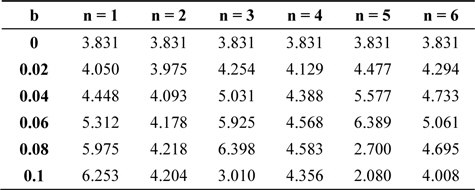
The position of the first minimum has been investigated for different values of b with respect to
[Table 2.] First minimum position on the good side with respect to z = 0
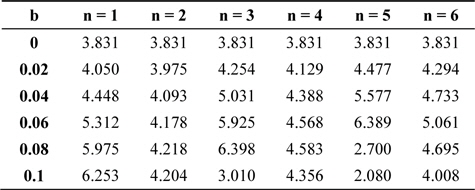
First minimum position on the good side with respect to z = 0
It is observed that for
For
Further, we observed a narrowing of the central maxima on the good side of the diffraction pattern, which renders in the resolution of two point objects that have widely varying intensities. A similar trend is noted for
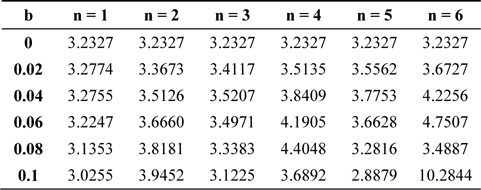
One of the important image quality criteria is full-width at half-maximum (FWHM) of apodized optical systems with semicircular arrays; it has been computed for different numbers of semicircular discrete elements and listed in Table 3 for different values of the asymmetric apodization parameter
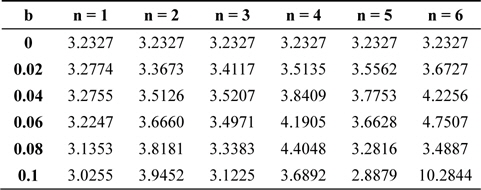
Full-wave half-maximum for different numbers of discrete elements (n) in a semicircular array of aperture with asymmetric apodization (b)
We conclude that the asymmetric apodization applied to 2D arrays of elements improves the resolution of optical systems. It is more important and convenient to modify an array of discrete semicircular elements into an asymmetrically apodized one in order to achieve a simultaneous suppression of sidelobes and sharpening of the central peak in circular antenna arrays. By employing asymmetric apodization for semicircular arrays of odd number of discrete elements, the resolution of the optical imaging system has been improved considerably. Pupil function capabilities in the redistribution of energy in the sidelobes or the central peak have been verified.
This technique is thus reliable, and the configuration of the circular aperture with semicircular arrays with opposite ends allows us to detect whether the good side is the right or the left side of the bright object and to detect the presence of the fade point object from the vicinity of the bright point object.