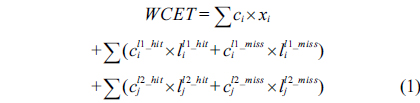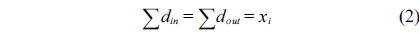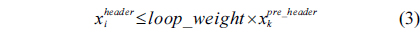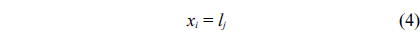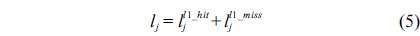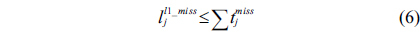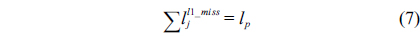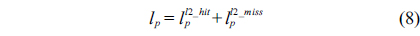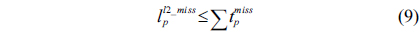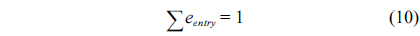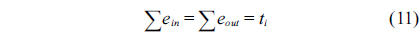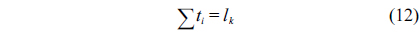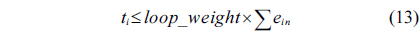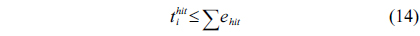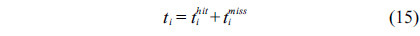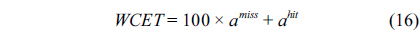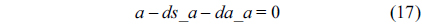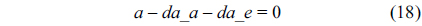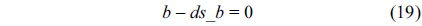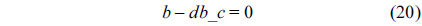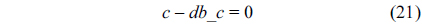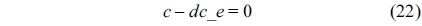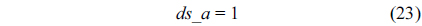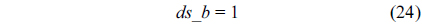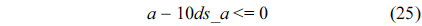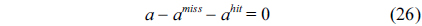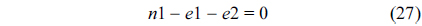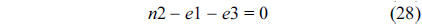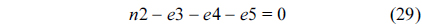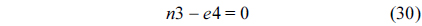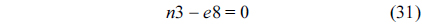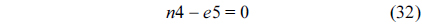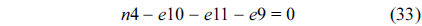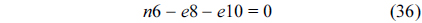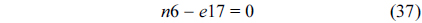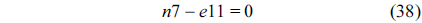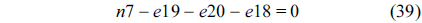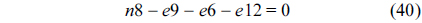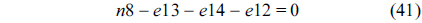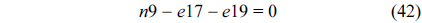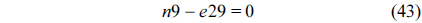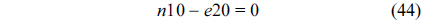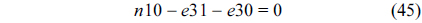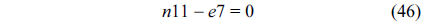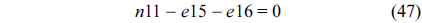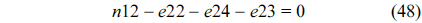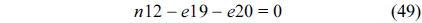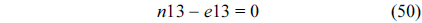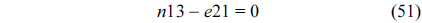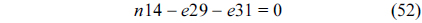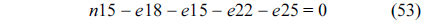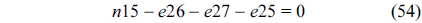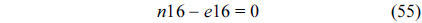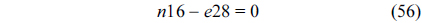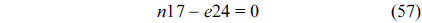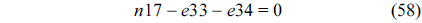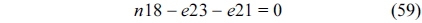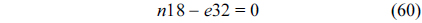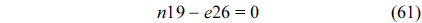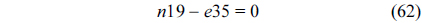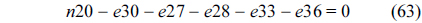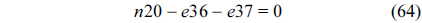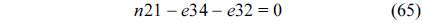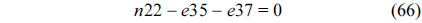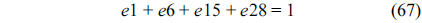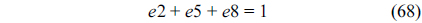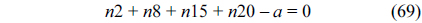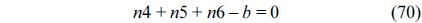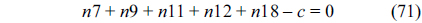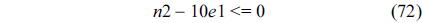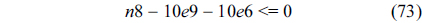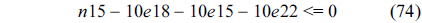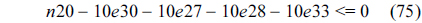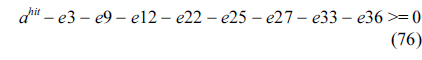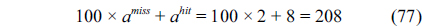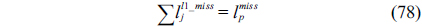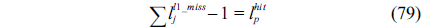In hard real-time systems, the success of the schedulability analysis depends on accurately obtaining the worstcase execution time (WCET) of the tasks. While a multicore processor can potentially benefit real-time systems for achieving better performance and energy efficiency, it is very challenging to obtain the WCET accurately on a multicore processor due to complex inter-thread interferences in shared resources on a multicore chip, such as a shared L2 cache.

Multicore WCET analysis has been actively investigated recently. Yan and Zhang [1, 2] proposed a coarsegrain approach to calculate the WCET of multicore processors with shared instruction caches. The worst-case inter-thread cache interferences and the WCET were calculated by an extended integer linear programming (ILP) approach, which modeled all the possible inter-thread cache conflicts [3]. While these two approaches [1-3] are safe, they may lead to overestimation of the WCET, because both approaches compute the worst-case instruction cache performance and the worst-case path separately. Also, these two approaches are limited to directedmapped instruction caches only, which do not support timing analysis of set-associative caches or data caches in their current forms.

Li et al. [4] estimated the potential conflicts in the shared instruction cache by progressively improving the lifetime estimates of the co-running tasks, which can support set-associative instruction caches, but not data caches. Li et al. [4], however, relied on an iterative process to compute the task interferences, which is very costly to compute, especially for a large number of cores.

Lv et al. [5] proposed combining abstract interpretation with model checking to estimate the timing bounds of programs running on multicore processors. The advantage of this approach is that it can consider the variable memory access delays due to both cache misses and memory bus contention. However, due to the use of a model checker, the number of states modeled can explode, making it either impractical or too expensive if the number of cores scales.

Recently, an approach based on the combined cache conflict graph (CCCG) [6, 7] was proposed to bound the worst-case inter-thread cache interferences in multicore processors. However, the CCCG-based approach has significant computational complexity. The number of cache states that need to be modeled in the CCCG grows exponentially with the increase of the number of cores, the set associativity of the shared cache, or the number of cache accesses of each concurrent thread (see Section Ⅱ-F for details). This makes it prohibitive to compute the WCET for multicore processors with a large number of cores.

To design an efficient, accurate, and scalable timing analysis method for multicore processors, this paper proposes three counter-based approaches to efficiently compute the WCET of programs running on multicore processors with different levels of accuracy and running time. The main contributions of this paper include the following:

(1) Identifying that the computational complexity of the CCCG-based approach is exponential and prohibitive in the case of large programs or a large number of cores.(2) Using abstract interpretation to predict cache behavior [8] and detect infeasible paths [9], which reduces the computational complexity of the CCCG-based approach.(3) Proposing a basic counter-based approach that can safely compute the worst-case cache behavior on shared L2 caches by comparing the number of cache line blocks mapped into a cache set with the associativity of the cache.(4) Enhancing the accuracy of the basic counter-based approach by excluding the cache line blocks on the infeasible paths and by avoiding counting mutually exclusive cache line blocks redundantly.(5) Proposing a hybrid approach by combining the enhanced counter-based approach and the CCCGbased approach to improve the accuracy of the WCET estimation.(6) Implementing and evaluating the three proposed counter-based approaches in terms of the WCET and running time, and comparing them with the CCCG-based approach.

In this paper, we have made several assumptions. First, in the multicore processor studied, each core is symmetric and single-threaded. Each core has private L1 instruction and data caches, and shares a unified L2 cache with other cores. Second, to focus on studying the timing of instruction cache behavior, the L1 data cache is assumed to be perfect so that there is no data cache interference on the shared L2 cache. However, it should be noted that our approach can also be easily applied to shared data caches by counting the worst-case number of data cache references of each cache set. Third, we assume all the threads running concurrently on different cores are independent of each other and do not share any instructions or data. In addition, we assume that both the buses between the caches and the shared memory are ideal, so the impacts of the worst-case bus delay and memory contention on the WCET [10] are not considered in this paper.

The rest of this paper is organized as follows. First, Section Ⅱ briefly describes the CCCG-based approach and identifies its computational complexity as exponential. Then, Section Ⅲ introduces the abstract interpretationbased techniques to reduce the computational complexity of the CCCG by predicting the cache behavior and excluding the infeasible paths. We present three counterbased approaches to bound the WCET of multicore processors in Section Ⅳ. Section Ⅴ describes the evaluation methodology, and Section Ⅵ gives the experimental results. Finally, we draw conclusions in Section Ⅶ.

The CCCG-based approach [6, 7] is based on the implicit path enumeration technique (IPET) proposed by Li et al. [11], and it extends the cache conflict graph (CCG) of the IPET into the CCCG in order to bound the worst-case cache interferences in a shared cache of a multicore processor.

The IPET calculates the WCET by solving an ILP problem. It is an efficient method of WCET analysis for uniprocessors without using explicit path enumerations. In the IPET, the WCET of a thread is represented by an objective function, which is subject to structural constraints, functionality constraints, and micro-architectural constraints. The structural constraints model the constraints from the control flow, while the functionality constraints specify the loop bounds and other path-related data-flow information, and the micro-architectural constraints represent the timing of the hardware components, including the caches. All these constraints are represented as equations or inequalities that can be automatically solved by an ILP solver.

The WCET of a thread running on a multicore processor with a shared L2 cache can be computed by maximizing the objective function shown in Eq. (1). More specifically, the WCET is defined as the sum of the timing cost of each basic block and the timing cost of accesses to each cache line block from both L1 and L2 caches. The timing cost of a basic block equals its execution latency multiplied by its execution count (i.e., the maximal number of times this basic block is executed). The timing cost of a cache line block is the sum of the latencies of a cache miss or hit at the corresponding level multiplied by the corresponding number of accesses to this cache line block. The symbols used in this paper are explained in Table 1.

The structural constraints are described following Eq. (2). Inequality (3) is the functionality constraint, which states that the upper bound of the execution count of a loop header block is equal to the product of the execution counts of the pre-header block and the weight of this loop. Eq. (4) describes the relationship between basic block B_i and L1 cache line block L_i contained in B_i. The cache constraints are demonstrated in Eqs. (5) to (9), where l_j and l_p are the execution counts of cache line blocks on the L1 cache and the L2 cache, respectively. For example, Eq. (5) indicates that the misses of an L1 cache line block are bounded by the execution count of this cache line block. Note that Eqs. (6) to (9) basically give the upper bound of the number of misses for a cache line block. They are derived from the CCCG, which will be explained in Section Ⅱ-C.

A CCG is created for each cache set in IPET. The vertices in the CCG are the cache line blocks mapped into the same cache set, and the edges describe the valid transitions between the cache line blocks according to the control flow of the thread being analyzed. However, the CCG can only represent the cache states and related transitions caused by cache line blocks from one thread. It needs to be enhanced in the following three regards to be able to model the behavior of a shared cache in a multicore processor. First, it should be capable of memorizing the historical cache accesses from all the threads. Second, it must represent the change of the cache state caused by a cache access from any thread. Last, it should be able to derive the cache states without violating the control flow and program semantics of any thread to obtain the WCET safely.

A CCCG significantly extends CCGs to satisfy the three requirements mentioned above for supporting timing analysis of a shared cache in a multicore processor. In a CCCG, each vertex represents a comprehensive cache state and is denoted by a tuple t(r:c) consisting of two sub-tuples r and c. The sub-tuple r(l₁, l₂, …, l_m) records the most recent cache access from each thread, where l_i is the most recent cache access from thread T_i, and m is the number of threads. The sub-tuple c(x₁, x₂, …, x_n) represents a cache state, where x_i represents the line block in cache way i and n is the associativity of the cache being modeled. The construction of the CCCG for a cache set begins with building the CCGs of this cache set for all the threads. The first state in the CCCG is initialized as t(s₁, s₂, …, s_m:ϕ₁, ϕ₂, …, ϕ_n), where s_i is the starting node in the CCG of the thread T_i, and Φ_i means that the i-th way of the cache set is empty. Other cache states are derived by traversing all the paths from the starting vertices to the end vertices of all the CCGs. For a cache state t_curr already existing in the CCCG, if the current cache access l_i,j of a thread T_i has an outgoing edge d_i leading to another cache access l_i,k in its CCG, a new cache state t_next is created by updating both sub-tuples r and c in t_curr with l_i,k. For example, if t_curr is represented as t(l₁, ..., l_i,j, ...l_m:x₁, …, x_i,j, ...x_n), tnext can be represented as t(l₁, ..., l_i,k, ...l_m:x₁, …, x_i,k, ...x_n). The update of the sub-tuple c can be implemented with different cache replacement policies, such as FIFO or LRU. Also, an edge is added from t_curr to t_next to indicate this transition. It should be mentioned that the creation of t_next must check its upper-level cache state in the case of an L2 cache. If the transition leads to an L1 cache hit, t_next is simply inherited from t_curr.

Since the CCCG describes the cache behavior on a shared cache caused by the cache accesses from all the co-running threads, it can produce the constraints to bound the worst-case cache access latency for a given thread by considering all the possible inter-thread cache interferences from other threads. The constraints generated from the CCCG are as follows.

Eq. (10) indicates that the sum of the execution counts of all the entry edges of the CCCG should be equal to 1. The structural constraint and the functionality constraint of the CCCG are shown in Eq. (11) and Inequality (13), respectively. Eqs. (12), (6), and (9) in Section Ⅱ-B describe the constraints of the relationship between the tuple in the CCCG and the line blocks involved in this tuple. Additionally, the constraints to bound the number of cache hits of the tuple in the CCCG are described in Eqs. (14) and (15).

For simplicity, we assume two threads T₁ and T₂ are running on a dual-core processor with a shared 2-way setassociative cache. Thus, the tuple t in our CCCG approach can be initialized as (S₁, S₂ : x, x), where S₁ represents the starting node in the CCG of the first thread T₁, S₂ denotes the starting node in the CCG of the second thread T₂, and x means the state for the current cache set is unknown. The next transition t_next can be derived by examining the left side of the tuple of the current vertex t_curr. If the current access from either T₁ or T₂ has any out_edge in its CCG, leading to the access of the next cache line block, then our approach updates t_next to represent the correct next cache set state. For an L1 cache, the right side records the most recent access to the most recent cache line.

However, for an L2 cache, the update of t_next must check its upper-level cache state. If the next address transition leads to an L1 hit, then the current L2 t_next will simply inherit the same state from t_curr.

Algorithm 1 takes the initialized state t and starts walking from the thread s₁. If the last access of thread s₁ has an out_edge leading to the next address access, then the next cache set state is generated. The new cache set state is initially inherited from t. To update the new cache set state, the algorithm first checks whether or not the upperlevel cache leads to a cache miss. If a cache miss happens at the upper-level cache, then a new cache state is updated based on the current level cache configuration. If a cache hit occurs at the upper-level cache, then the new cache state remains intact as the cache state in t. The algorithm then uses t_next to derive a new state. The termination condition of the algorithm is that the last accesses from all threads have no out_edge to go to, which indicates that the last access has reached the end of the CCG in each cache line.

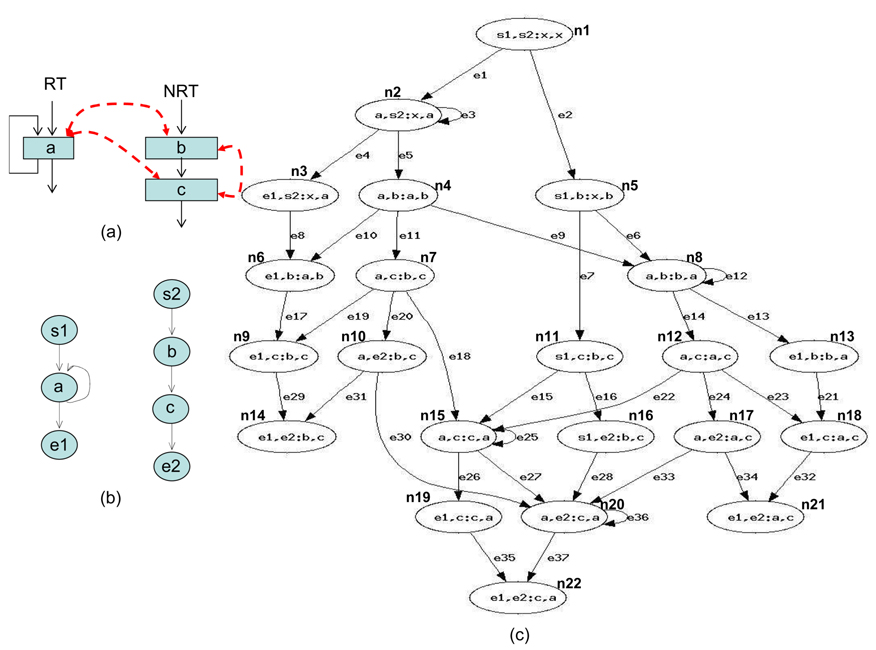
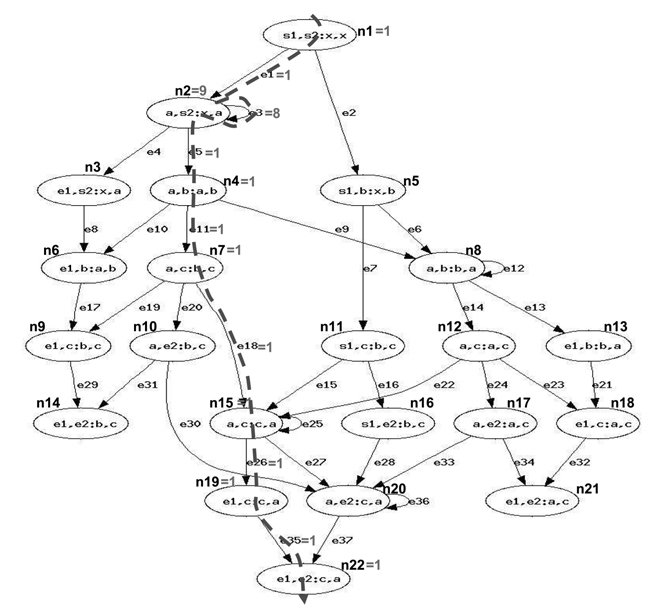
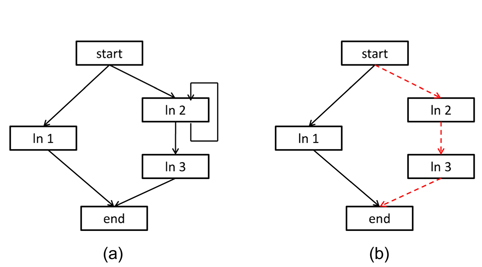
Fig. 1 gives an example to illustrate how to apply the CCCG for the WCET analysis of parallel programs running on a multicore processor with a shared cache. For simplicity, we assume that there are two threads, a realtime thread (RT) and a non-real-time thread (NRT)—the CCCG can be applied to multiple RTs as well. While the RT has only one instruction a, the NRT has two instructions, b and c. Assume the cache is 2-way set-associative with one set.

Thus, a, b, and c will all be mapped to the same cache line. Also, we assume the cache hit latency is 1 cycle and that the cache miss latency is 100 cycles. Fig. 1(a) shows the control flow graphsa (CFGs) for the RT and NRT, while Fig. 1(b) depicts the CCGs for the RT and NRT, and Fig. 1(c) shows the CCCG, which is constructed automatically by applying Algorithm 1 to the CFGs and CCGs of both threads.

The following objective function is derived from Eq. (1).

Structural constraints are derived from Eq. (2).

First, we construct the structural constraints for the RT. In the following equations, d represents an edge, and ds_a means that the edge starts from the beginning point (i.e., s) to an instruction a. Similarly, da_e means that the edge starts from the instruction a to the end of the program (i.e., e).

Also, we can construct structural constraints for the NRT as follows.

For each thread, we assume that each of them executes only once.

We also assume that the loop in the RT thread executes no more than 10 iterations, which is based on Eq. (3).

Cache constraints are obtained from Fig. 1(c).

The following equation describes the constraints, i.e., the sum of instruction a's different states is equal to the execution counts of instruction a. This is derived from Eq. (5).

The following equations specify the flow constraint that the sum of in-flow and out-flow must be equal to the execution counts of each node, which are derived from Eq. (10).

The RT thread executes only once, which leads to the following equation based on Eq. (10).

Similarly, the NRT also executes only once, leading to the following equation.

The sum of all the nodes that execute instruction a must be equal to the execution counts of instruction a, which leads to the following equation derived from Eq. (12).

Similarly, the sum of all the nodes that execute instruction b also must be equal to the execution counts of instruction b, which leads to the following equation.

Also, the sum of all the nodes that execute instruction c must be equal to the execution counts of instruction c, so we have the following equation.

The following equations are derived from Eq. (13).

The total cache hits of instruction a should be equal to the sum of all the edges that lead to a possible cache hit for instruction a. Thus, we can derive the following equation based on Eq. (14) to bound the number of cache hits.

Fig. 2 shows the WCET path for the example. The final result from ILP (i.e., the WCET) is 208, which can be derived from Eq. (77).

As can be seen from the example shown in Fig. 1, the CCCG is very complicated, even for very simple code. The complexity of the CCCG is determined by the number of tuples in it. The increase of the number of tuples not only increases the time to build the CCCG, but also increases the timing complexity of deriving the constraints. As mentioned in Section Ⅱ-C, the tuple records the most recent cache accesses from the CCGs of all the threads, and stores the cache states caused by these cache accesses. Since there is no fixed timing order between the cache accesses from different threads, and different orders of accesses to the same set of line blocks may result in different states of a cache set, a tuple can be considered as a permutation of the line blocks from the CCGs of all the threads.

Without losing generality, we assume that there are N threads running on a multicore processor with a shared cache. The size of the shared cache is C; the cache block size is B; and the associativity is S. There are M connected line blocks in the CCG of each thread for a given cache set—M is the minimal number of the cache line blocks of any thread, if different threads have different numbers of cache line blocks in a cache set. In order to create a tuple for the CCCG of this cache set, one line block is selected from each CCG first, resulting in MN possibilities. Then, the selected line blocks are fully permuted, leading to N! permutations. As a result, the worst-case number of tuples in the CCCG is M^N × N!. Hence the computational complexity of building a CCCG is O(M^N × N!), and the worst-case timing complexity of generating the constraints is also O(M^N × N!) if all the tuples are traversed. As the cardinality of the cache set is equal to C/(B × S) and a CCCG is created for each cache set, the computational complexity of the CCCG-based approach is O(C/(B × S) × (M^N × N!)). It is clear that the computational complexity increases exponentially with increase in the number of the threads, making it prohibitive to compute the WCET of a thread running on a multicore processor with a large number of cores.

To decrease the computational complexity of the CCCG-based approach, we propose excluding the cache line blocks that will not impact the worst-case cache analysis from a CCCG. Specifically, there are two types of line blocks that can be excluded from the CCCG:

(1) The accesses to the cache line blocks that always result in misses even without the inter-thread cache interferences, because they cannot be worsened by inter-thread cache interferences.(2) The cache line blocks on infeasible paths of a thread.

We use the cache analysis method based on abstract interpretation proposed by Theiling and Ferdinand [8] to detect the first type of cache line blocks. It applies the abstract interpretation framework to describe the cache semantics, including the control flow representation, abstract cache state, and abstract cache update function. Three types of analyses are used to categorize each memory reference. The may analysis is used to detect cache line blocks that are guaranteed to be absent in the cache, to which the accesses always result in cache misses.

Gustafsson et al. [9] proposed a method of abstract execution to automatically detect infeasible paths. Abstract execution is also based on abstract interpretation. It executes the program in the abstract domain, with abstract values for the program variables and the abstract versions of the operators. The method used to detect infeasible paths is a variation of abstract execution. It includes specific recorders, collectors, update points, update operations, and abstract state transition functions. This method finds sequences of nodes that are never executed during the same iteration of an abstract domain. The line blocks that are detected to be on the infeasible paths are excluded from the building of the CCCG.

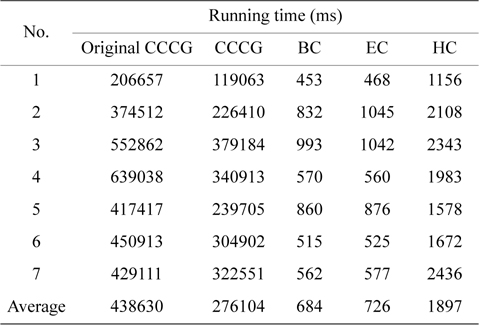
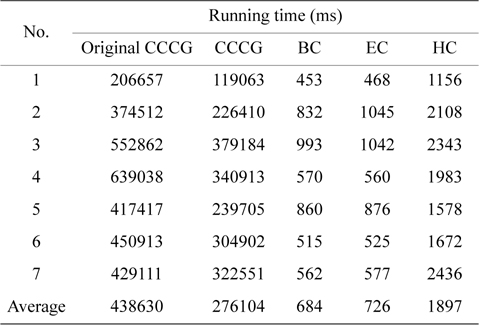
These approaches are expected to reduce the computational complexity of the CCCG. Table 2 in Section Ⅵ-D demonstrates that they do in fact reduce the running time of all the experiments by 38.1% on average compared to the original CCCG-based approach. However, the theoretical computational complexity of generating a CCCG is still exponential because the mechanism of building a CCCG is not changed. The CCCG-based approach is thus practically infeasible for obtaining the WCET of large programs running on multicore processors with a large number of cores, even with the exclusion of unnecessary cache line blocks from the CCCG. Therefore, it is necessary to explore a new approach, which not only has much less complexity than the CCCG-based approach, but also computes the WCET safely with an accuracy that is ideally the same as or very close to that of the CCCG-based approach.

To find an efficient, scalable WCET analysis approach for shared caches of multicore processors, we have extensively studied the cache access and interference behavior of concurrent threads. We observe that with an increased number of cores (and threads), it becomes very likely that the conflicting cache accesses from different threads exceed the number of set associativity, which is referred to as interference saturation in this paper. In this case, we also observe that it is very likely for the concurrent threads to interleave their accesses in a way to result in cache misses, i.e., the worst-case scenario. This motivates us to develop a simple yet effective approach by counting the number of cache line blocks mapped to each cache set across all the co-running threads, based on which we can derive a safe upper bound of the worst-case shared cache performance.

To study the cache behavior based on the relation between the associativity of a cache set and the number of line blocks mapped into it from all the co-running threads, we conduct some experiments in a simulated multicore environment by extending SimpleScalar [12]. The memory hierarchy of the simulated environment and the benchmarks used in the experiments are the same as the experimental framework described in Section V-A. The experiments examine the interference-saturation-miss probability, which is defined in Definition 1. The experiments are conducted on a 2-core processor, a 4-core processor, and an 8-core processor. Fig. 3 demonstrates the averaged interference-saturation-miss probability in all experiments of 2 cores, 4 cores, and 8 cores. We observe that the probabilities of 4 cores and 8 cores are much higher than that of 2 cores. For example, the probability for the benchmark select is only 35.25% in the case of 2 cores, but it rises to 83.5% for 4 cores, and 90.54% for 8 cores. The last three columns of Fig. 3 show the averaged results for all the benchmarks. The averaged interferencesaturation- miss probability of all the benchmarks is almost 90% for 8 cores, and more than 80% for 4 cores.

DEFINITION 1. Interference-Saturation-Miss Probability: The probability of the accesses to a cache line block of a shared L2 cache resulting in cache misses if the set associativity is fewer than the total number of cache line blocks assessed by all the concurrent threads.

It is important to note that the results in Fig. 3 are just simulated results based on particular inputs, since it is generally very difficult to exhaust all inputs to derive the actual worst-case cache behavior, if not possible. However, it should be noted that the worst-case interferencesaturation- miss probability must be no better than what we have observed in Fig. 3. On the other hand, if the number of cache line blocks mapped to a cache set across all the threads is fewer than the set associativity, then the references to these cache line blocks can only result in cold misses in the worst case, which can be easily identified identified statically. These observations motivate us to develop a more efficient counter-based approach to estimate the worst-case inter-thread L2 cache misses safely and accurately.

We propose a counter-based approach to efficiently estimate the worst-case cache behavior of a multicore processor with a shared cache by exploiting the fact that the interference-saturation-miss probability is very high, especially when the number of cores is large. The basic idea of the counter-based approach is to compare the associativity of a cache set with the number of line blocks mapped into it across all the concurrent threads. We associate a counter with each cache set to count the number of cache line blocks mapped to it across all the concurrent threads. The worst-case cache behavior can then be computed according to the following rules.

(1) Rule I: If the number in the counter is larger than the associativity of a cache set, the references to any cache line block in this cache set are classified as always miss [13], which means all the references to this cache line block will result in cache misses.(2) Rule II: If the number in the counter is smaller than or equal to the associativity of a cache set, the references to the line blocks in this cache set are classified as first miss [13], which indicates that only the first reference to a cache line block is treated as a cache miss (i.e., cold miss), and all remaining references will result in cache hits.

This approach is referred to as the basic counter-based approach. Clearly, this approach can safely estimate an upper bound of the shared cache performance, because the interference-saturation-miss probability cannot be more than 100%, which has been conservatively assumed in Rule Ⅰ. In Rule Ⅱ, based on the assumption, the number of cache accesses that may lead to inter-core interferences can actually fit into the cache set; therefore, they can only suffer from cold misses, which is already the worst-case scenario.

The main procedure to implement the counter-based approach is almost the same as the IPET, except that the CCG and related cache constraints are only built for the higher-level separated cache, i.e., the private L1 cache. The cache constraints on the shared cache are described in two equations by modifying Eq. (7). Specifically, Eq. (78) represents the cache constraint of the line blocks classified as always miss, and Eq. (79) describes the cache constraint of the line blocks classified as first miss.

Complexity Analysis: We estimate the computational complexity of the basic counter-based approach by following the assumptions made in Section Ⅱ-F. As the counter for a cache set is calculated by checking all the cache line blocks in the CCGs for this cache set from all the threads, the complexity of calculating one counter is equal to O(N × M). Hence, the complexity of calculating all the counters is O(C/(B × S) × (N × M)), because each cache set has a counter. Furthermore, the complexity of the classification of the worst-case cache behavior based on the counter is O(C/(B × S) × (N × M)). As a result, the computational complexity of the basic counter-based approach is O(C/(B × S) × (N × M)), which has linear relationship with the number of cores or the number of cache accesses.

While the basic counter-based approach can greatly reduce the complexity of analysis, it may lead to overestimation. There are at least two factors that may lead to an overestimated WCET. First, the cache line blocks on the infeasible paths of each thread should not be taken into account. Second, the line blocks on the mutually exclusive paths in a thread should not be calculated in the same counter, because they cannot happen at the same time. We thus propose an enhanced approach to solve these problems. To address the first problem, we use the abstract execution proposed by Gustafsson et al. [9] to detect and eliminate the infeasible paths of all the threads before the calculation of the counter starts. To solve the second problem, we use data flow information extracted by the compiler to detect mutually exclusive paths, and the cache line blocks accessed by instructions from those paths are only counted once to derive the worst case. The enhanced counter-based approach consists of four major steps:

(1) Construct a CCG for each thread on a given cache set.(2) Detect and eliminate the back-edges of the loops in each CCG to transfer the CCG into a direct acyclic graph.(3) Find the longest path from the starting vertex to the ending vertex in each CCG by using the dynamic programming algorithm, and then calculate the number of cache line blocks on the longest path as the counter of the corresponding thread for the given cache set.(4) Add up the counters of all the threads, and the result is the final counter for the given cache set.

Fig. 4 illustrates an example of enhancing the calculation of the counter. Fig. 4a is a CCG of a thread on a given cache set. It contains three line blocks and a loop involving the line block ln2. In the basic counter-based approach, the counter should be equal to 3. Following step 2 in the enhanced counter-based approach, the backedge of the loop from ln2 to ln2 is detected and eliminated. The resulting CCG is shown in Fig. 4b.

It is clear that the longest path from the start vertex to the end vertex is start ln2 ln3 end, as marked by the dotted line, and there are only two line blocks on this path. Therefore, the counter of the thread on the cache set is 2, not 3.

The computational complexity of the enhanced approach counter-based approach is equal to the computational time complexity of the basic counter-based approach plus the computational complexity of finding a longest path in each CCG, which has a linear relationship with the number of vertices of the CCG.

Although the shared cache is accessed by all the threads running in a multicore processor, not all the cache sets are accessed by all the threads. It is possible that a given cache set is accessed by only one or two threads. The computational complexity of building the CCCG in this case is small and acceptable. Moreover, if a cache set is accessed by only one or two threads, the interferencesaturation- miss probability is likely to become smaller, so applying the counter-based approach in this case may lead to the overestimation of cache misses.

We propose a hybrid approach by combining the enhanced counter-based approach and the CCCG-based approach. Specifically, the cache sets in a shared L2 cache are first classified into two categories: one consisting of the cache sets accessed by more than 2 threads, and the other including the cache sets accessed by up to 2 threads. For the first type of cache sets, the counter-based approach is still used to estimate the worst-case cache behavior. However, for the second type of cache sets, the CCCG-based approach is used to bound the worst-case cache misses more accurately, because the CCCG-based approach can still run efficiently with only two threads, and the computational complexity is increased exponentially and hard to afford with a large number of threads.

As the computational complexity of the hybrid counterbased approach is dominated by the cache sets applied to the CCCG-based approach, the computational complexity of the hybrid counter-based approach is O(C/(B × S) × (M²)) with N = 2, following the assumptions and notations used in Section Ⅱ-F.

The experimental framework of our multicore WCET analysis approach consists of three main components: the front end, the back end, and the ILP solver. The front end compiles the benchmarks to be analyzed into COFF format binary code by the GCC compiler, which is translated into MIPS ISA. Then, it obtains the global CFG and related information of the instructions by disassembling the binary code generated by the compiler. The back end performs static cache analysis [14] by using the three counter-based approaches. A commercial ILP solver- CPLEX [15] is used to solve the ILP problem to compute the WCET.

Our experiments are mainly focused on a 4-core processor with a shared L2 cache simulated by an extended SimpleScalar simulator. In this quad-core processor, each core has its own L1 instruction cache and L1 data cache. The L1 instruction cache is directed-mapped, its total size and cache block size are 512 bytes and 8 bytes, respectively, and its miss penalty is 4 cycles. The L1 data cache is assumed to be perfect, since our evaluation focuses on the analysis of the cache behavior of the instructions. The shared L2 cache is 2-way set-associative, and its size is 2048 bytes. The block size of the shared L2 cache is 16 bytes, and its miss penalty is 100 cycles.

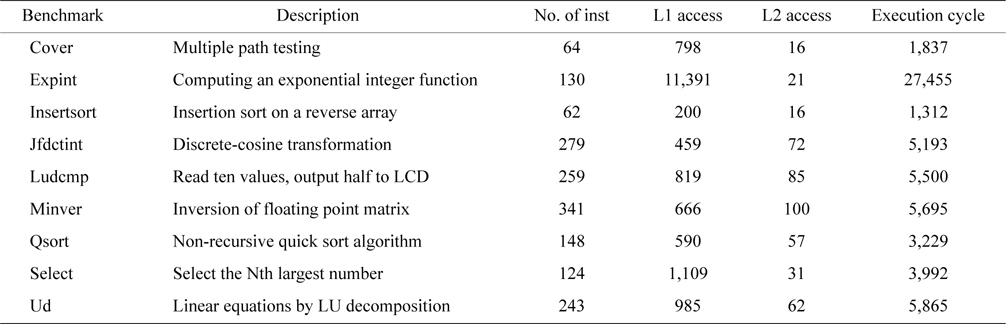
The benchmarks are from Mälardalen WCET benchmarks [16], whose salient characteristics are described in Table 3. Some benchmarks are selected for each experiment. Each benchmark is regarded as a thread running on a core of the multicore processor.

In our experiments, we studied four different schemes based on different WCET analysis approaches as follows:

● The CCCG scheme: The CCCG-based approach [6, 7] is used to calculate the WCET in this scheme. Two techniques based on abstract interpretation mentioned in Section Ⅲ are used to reduce the computational complexity of the original CCCG-based approach● The basic counter (BC) scheme: The basic counterbased approach described in Section Ⅳ-B is used to calculate WCET in this scheme.● The enhanced counter (EC) scheme: The enhanced counter-based approach described in Section Ⅳ-C is used to calculate WCET in this scheme.● The hybrid counter (HC) scheme: The hybrid counterbased approach described in Section Ⅳ-D is used to calculate WCET in this scheme.

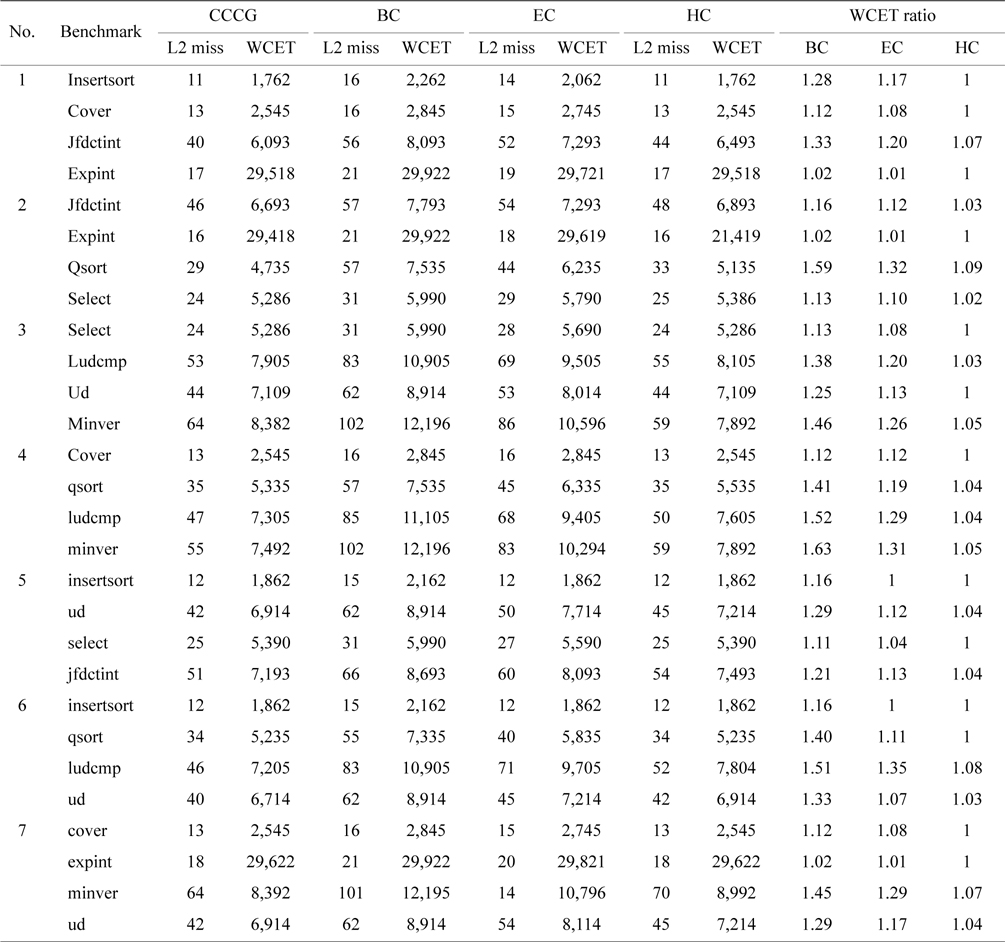
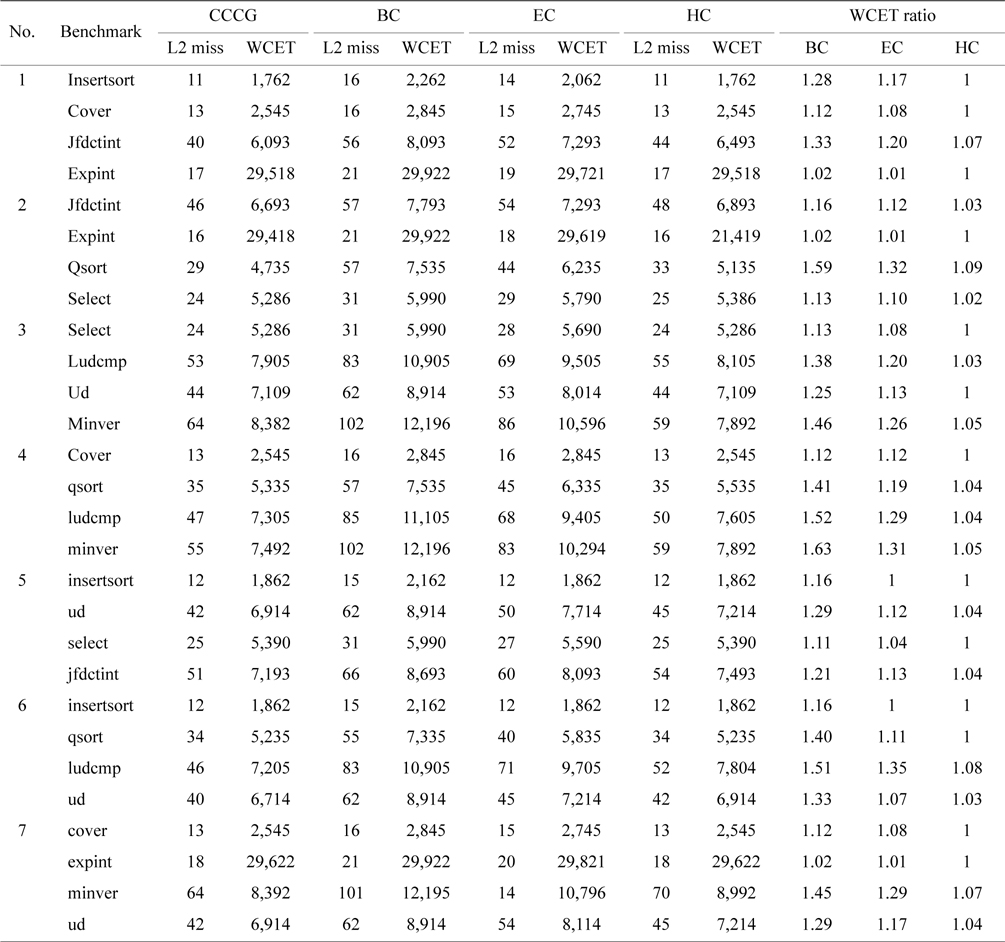
We have conducted seven experiments to compare the WCET and the worst-case L2 cache misses among all the four schemes on the 4-core processor. Each benchmark of a group is selected from the list of benchmarks shown in Table 3. Table 4 compares the worst-case L2 cache misses and the WCET of the benchmarks of the BC scheme, the EC scheme, and the HC scheme with the CCCG scheme. The last three columns give the ratios of the WCETs of three counter-based schemes to the WCET of the CCCG scheme.

As shown in Table 4, the WCETs of the BC scheme are much larger than that of the CCCG scheme. For example, the estimated WCETs of the benchmark qsort of the BC scheme are larger than those of the CCCG scheme by 59.1%, 41.2%, and 40.1% in Experiments 2, 4, and 6, respectively. On average, the estimated WCET of the BC scheme is 29.7% larger than that of the CCCG scheme.

The difference between the BC scheme and the CCCG scheme is caused by the overestimation of the worst-case L2 cache misses from the basic counter-based approach. First, some cache line blocks on the infeasible paths or mutually-exclusive paths are counted unnecessarily. If the value of the overestimated counter is larger than the associativity of this cache set, some cache accesses to this cache set are estimated as cache misses by mistake. SecThe difference between the BC scheme and the CCCG scheme is caused by the overestimation of the worst-case L2 cache misses from the basic counter-based approach. First, some cache line blocks on the infeasible paths or mutually-exclusive paths are counted unnecessarily. If the value of the overestimated counter is larger than the associativity of this cache set, some cache accesses to this cache set are estimated as cache misses by mistake. Second, if the line blocks mapped into a cache set are from only one or two threads, the probability of an inter-thread L2 cache interference is very low, if not zero, because a thread is more likely to reuse its cache content (i.e., hits) if there are few interferences from another thread, or if there are none at all. So, applying the basic counter-based approach will possibly lead to the overestimation of L2 cache misses than the CCCG-based approach.

As demonstrated in Table 4, the enhanced counterbased approach always returns a tighter number of estimated L2 cache misses than the basic counter-based approach, leading to more accurate WCET. For example, the estimated WCET of qsort of the EC scheme in Experiment 2 is reduced by almost 30% compared with that of the BC scheme. On average, the estimated WCET of the EC scheme is only 14% larger than that of the CCCG scheme. The main reason is that although the enhanced counter-based approach tightens the estimated WCET by calculating the counter of the cache set more accurately, it still leads to overestimation of the L2 cache misses if a cache set only contains the line blocks from one or two threads, in which case, the interference-saturation-miss probability is low.

Table 4 also compares the worst-case L2 cache misses and the WCET between the HC scheme and the CCCG scheme. It is clear that the difference between the HC scheme and the CCCG scheme is even smaller, and the estimated WCETs of some benchmarks are actually the same in both schemes, such as insertsort, cover, and expint in Experiment 1. The estimated WCET of the HC scheme is only 2.65% larger than that of the CCCG scheme on average, indicating that the HC scheme can predict the worst-case shared cache performance very tightly. However, the HC scheme is still not as accurate as the CCCG-based approach, because the worst-case interference-saturation-miss probability may not be 100%, even if there are more than 2 threads.

Table 2 compares the running time of all the experiments of the BC, EC, HC, and CCCG schemes, along with the original CCCG-based approach, which does not use any of the complexity-reduction techniques described in Section Ⅲ. The averaged running time in the BC and EC schemes are 684 and 726 ms, respectively, while the averaged running time of the CCCG scheme is more than 2 × 10⁵ ms. This demonstrates that the counter-based approaches significantly reduce the computational complexity of the multicore WCET analysis. As the hybrid counter-based approach applies the CCCG-based approach to a part of the cache sets, its averaged running time increases to 1897 ms. However, it is still much less than that of the CCCG-based approach. On average, the EC and HC schemes reduce the running time of the CCCG scheme by more than 380 and 150 times, respectively.

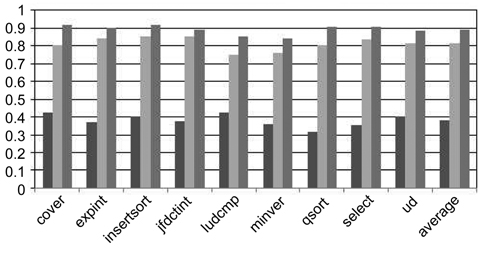
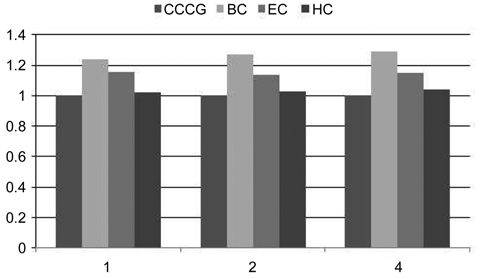
In order to study the impact of the set associativity of a shared L2 cache on the timing analysis, we varied the associativity of the shared L2 cache from 1 to 2 and 4. As shown in Fig. 5, the associativity results of 1 and 4 are similar to the associativity results of 2. Also, the difference between the EC and HC schemes becomes smaller when the associativity is increased from 1, 2 to 4. The differences are 13.27%, 11.35% to 10.59%, respectively. The main reason is that the probability of a cache set containing line blocks from only one or two threads decreases with the increase of the set associativity.

Following the trend of adopting multicores for desktop and server computing, the performance improvement of future real-time embedded systems is likely to depend on the increase of the number of cores. Therefore, it becomes increasingly important to design an efficient and scalable timing analysis method to safely and accurately estimate the WCET for hard real-time tasks running on multicore processors with shared resources. While there have been several research efforts on multicore timing analysis [1-4, 6], they have either been limited to instruction caches only, or have significant computation cost that is not scalable.

This paper proposed three counter-based approaches to significantly reduce the complexity of WCET analysis for shared caches in multicores, while achieving accuracy close to the CCCG-based approach with guaranteed safety. All three of these approaches are based on our empirical observation that in a multicore processor, especially in multicores with more cores, it is very likely for the concurrent threads to interleave their accesses to a shared cache in a way that results in inter-core cache misses, i.e., the worst-case scenario. The basic counter-based approach uses a counter associated with each cache set to compare the worst-case number of line blocks mapped into a cache set with its associativity. It predicts the worst-case cache behavior of the line blocks in the cache set according to the comparison result. The enhanced counter-based approach uses some techniques to enhance the accuracy of calculating the counters. Furthermore, a hybrid approach combines the enhanced counter-based approach and the CCCG-based approach to further improve the accuracy of the estimation.

Our experiments demonstrate that the enhanced counterbased approach overestimates the WCET by 14% on average compared to the CCCG-based approach on a 4- core processor, while its running time is less than 1/380 that of the CCCG-based approach on average. The hybrid counter-based approach reduces the overestimation to only 2.65%, while its averaged running time is less than 1/150 that of the CCCG-based approach.

In future work, we will extend the counter-based approaches to data cache analysis as well. Also, we plan to quantitatively evaluate the scalability of different counter-based approaches with more cores.