The energy dependence of cross sections is rather complex. To represent some reactions of resonant nuclides accurately, more than 100,000 energy points are required. Most nuclear codes cannot handle this vast amount of data. So, the pointwise cross sections are averaged over energy groups to form multigroup cross sections. These group constants depending on the energy group structure and weight function can be used for specific types of problems, such as thermal reactors, fast reactors, fusion problems or shielding calculations.
The number of energy groups also has a significant impact on the computations from two important aspects: accuracy and computation time. A trade-off exists between these two parameters. To mitigate these contradictions the selection of energy group structure becomes crucial. The choice of such structure is quite difficult due to four important physical phenomena in the reactor which shall be taken into account. These phenomena include: fission, slowing down and diffusion, resonance absorption and finally thermalization of neutrons. The conventional procedure to select energy structure is dividing energy into equal lethargy width groups in fast and thermal energy regions. In resonance energy region, groups are taken according to the main resonances of materials [1].
Several studies have been performed toward the selection of energy structure. Pazirandeh and Tabesh [2] studied the impact of increasing the number of energy groups in the resonance region. A sensitivity study on the group structure was carried out by Sanggene Han [3] for high temperature reactor analysis. Eventually Mosca et al. [4] used an adaptive approach to select energy meshes based on desired precision and calculation time.
In current research, the WIMSD-5B code is used to study the effect of energy group structure on the integral results of MOX thermal lattices. A brief description of this code and its original library has been given in section 2.1. The original WIMS library [5] is a 69 group set which can be used in a wide range of reactor types [6]. The WIMS energy group structure and those derived from it (e.g., 70 energy groups used in CASMO) have been widely used not only in academic investigations, but also for production calculations for light water reactors.
In this paper, we have used a heuristic optimization method for selection of group energy boundaries to obtain an optimized structure suitable for MOX thermal lattices. Particle swarm optimization (PSO) [7] which is a population based stochastic optimization technique (refer to section 3.3) is used for this purpose.
The contents of the paper are organized as follows. In the first part, WIMS and NJOY codes are described briefly. The specifications of benchmark problems and also the procedure of the work are described in section 3, and finally the results generated by the PSO method are presented in section 4. We summarize this work with a discussion in section 5.
The Winfrith Improved Multigroup Scheme (WIMS) code [8] was widely used for reactor calculations of a wide variety of thermal reactors. It consisted of a lattice transport code and the associated library. Temperature dependent thermal scattering matrices for a variety of scattering laws are included in the library for the principal moderators which include hydrogen, deuterium, graphite, beryllium and oxygen. The resonance treatment is based on the intermediate resonance (IR) approximation and the equivalence theorems.
The collision theory procedure gives accurate spectrum computations in the 69 groups of the library for the principal regions of the lattice using a simplified geometric representation of lattice cells. The computed spectra are then used for the condensation of cross sections to the number of groups selected for the solution of transport equation in detailed geometry.
The solution of the transport equation is provided either by use of the Carlson DSN method or by collision probability methods. Leakage calculations including an allowance for streaming asymmetries may be made using either the diffusion theory model or the more elaborate B1-method. The output of the code provides eigenvalues for the cases where a simple buckling mode is applicable or cell-averaged parameters for use in overall reactor calculations. Various reaction rate edits are provided for direct comparison with experimental measurements. It is worth noting that the WIMSD-5B code has more capability to use flexible energy group structure compared with its predecessor WIMS-D/4.
The WIMS library was first proposed in 1966. It uses a 69 group structure comprising:
14 groups in fast energy range (10 MeV to 9.118 KeV) with equal lethargy width of 0.5 to represent the Fermi age in light water and to cover fast fission of U-238 [6]
13 groups in resonance energy range (9.118 KeV to 4 eV), group boundaries are selected to locate important resonances of U-238 (6.7, 20 and 33 eV) at their lethargy midpoint
42 energy groups in thermal energy range (below 4 eV) including 12 groups clustered around the 1.05 resonance of PU-240 and 5 groups around the 0.3 eV resonance of PU-239 for treating the resonances located in this range.
2.2 NJOY Data Processing System
The NJOY System [9] is a modular computer code designed to read evaluated nuclear data files in ENDF format, process the data, and output the results as libraries to be used in various applications. This code uses sophisticated methods for resonance reconstruction using multi-level Breit-Wigner resonance parameters, Doppler broadening by accurate point kernel method, group to group thermal scattering matrices and special thermal law treatment, flux weighted fission fraction vectors, and a weighting flux produced by a point solution of the slowing down problem that accurately accounts for broad and intermediate resonance effects.
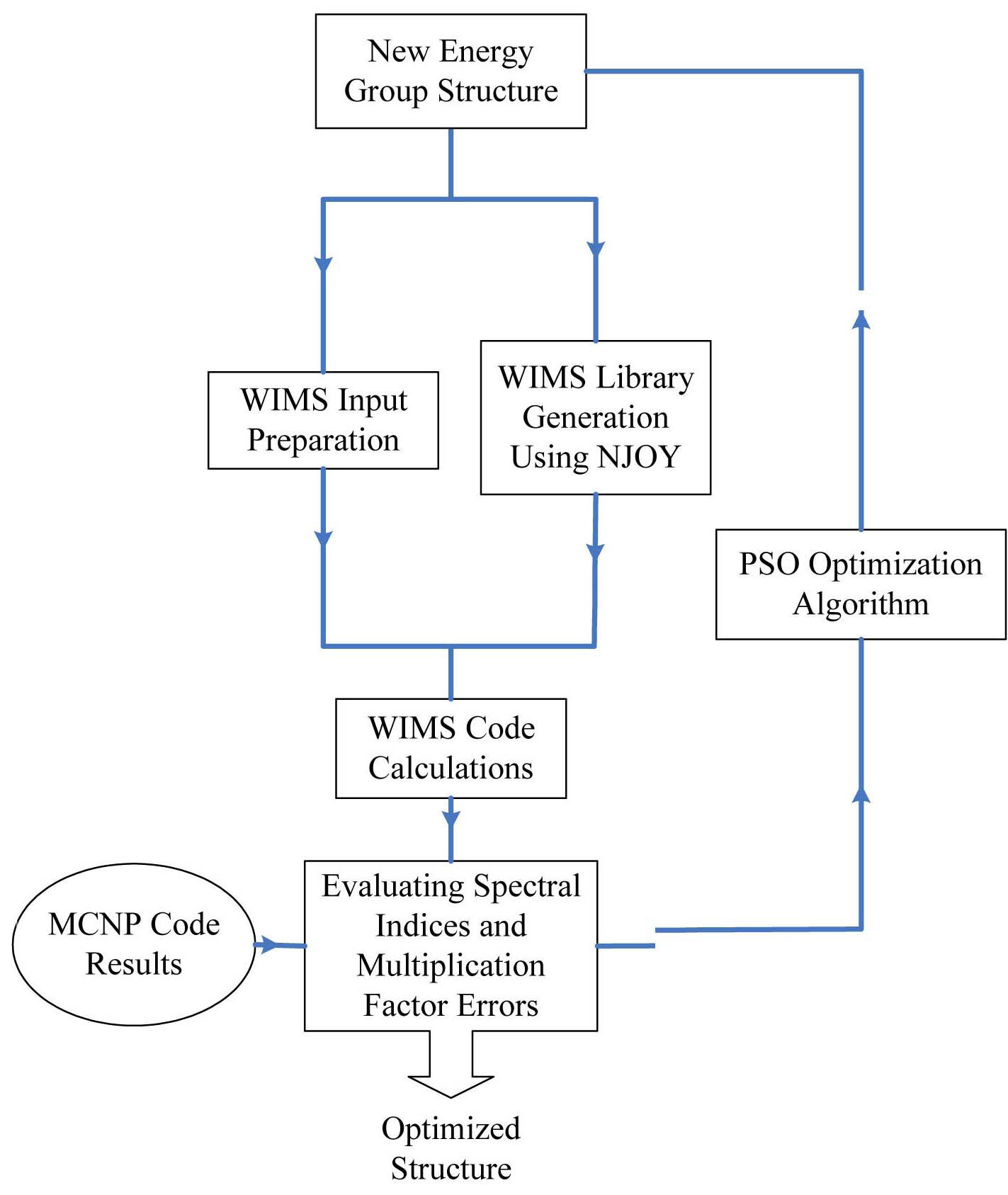
The methodology implemented in this paper for coupling the multigroup neutron cross section generation and transport calculation to investigate the optimized energy group structure is shown in Fig. 1. As seen in this figure, at first, the energy boundaries are selected by the optimization algorithm. In the next stage, the 69 group cross section library based on the specified energy structure is generated using the NJOY code system. Afterwards, multiplication factor and reactions of U-235 and U-238 are calculated using the WIMSD-5B code. An interface program was
written using Fortran 90 language to read the output of WIMS and calculate the spectral indices. The multiplication factor and the calculated spectral indices are compared against the MCNP code [14] results. To minimize the discrepancy of the results due to input data, the processed
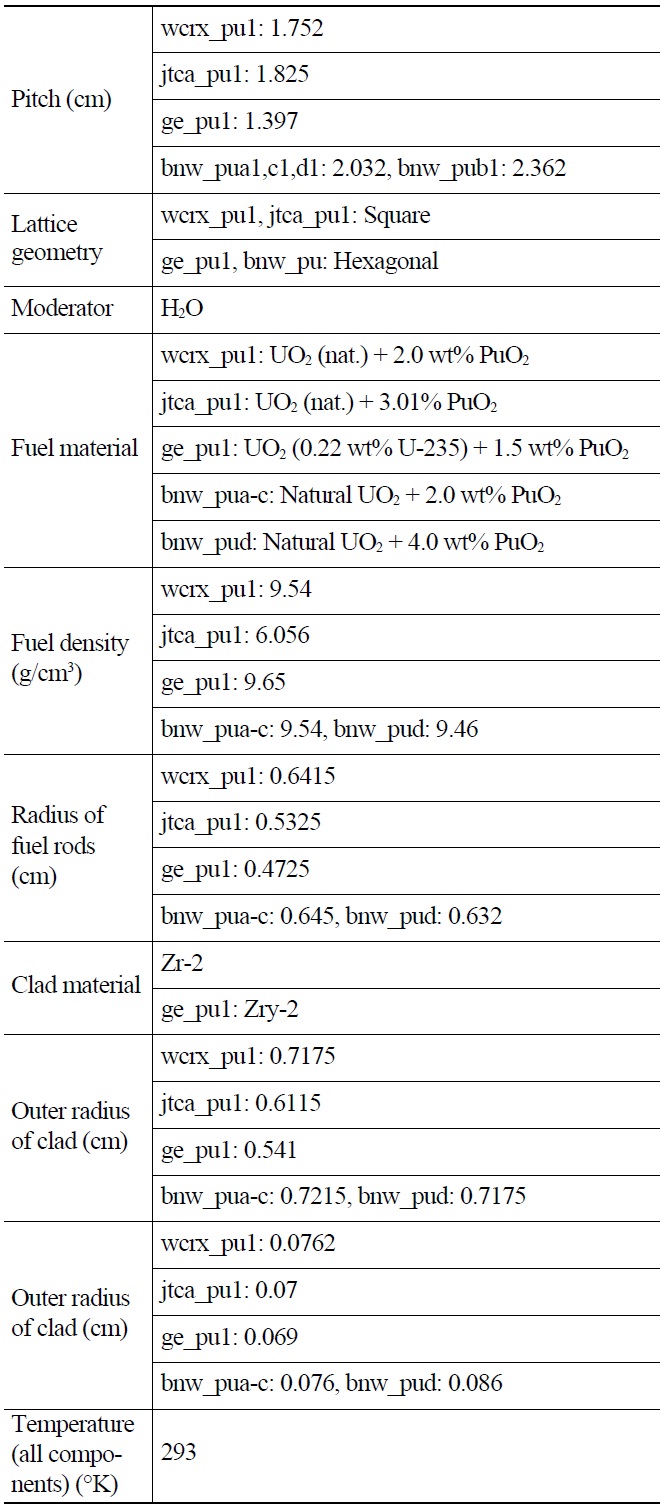
[Table 1.] General Specifications of Benchmark Lattices
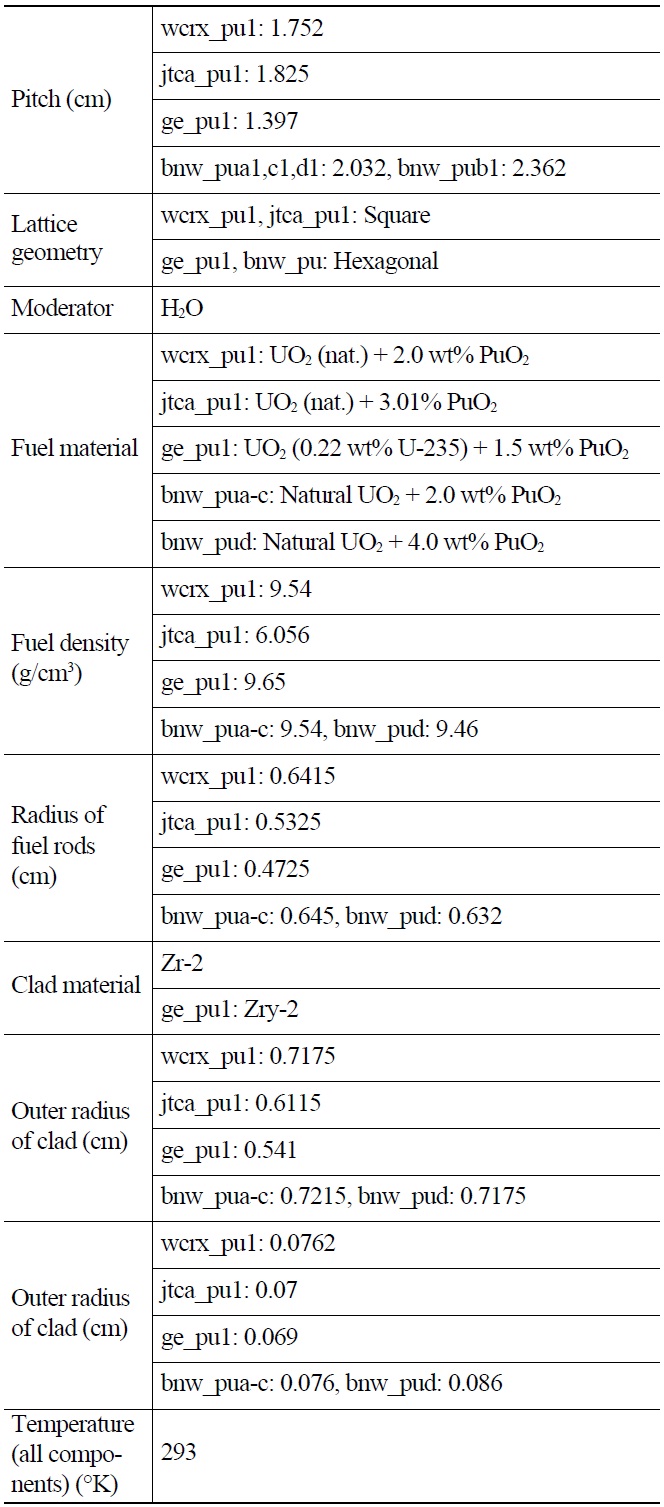
General Specifications of Benchmark Lattices
pointwise cross sections are converted to MCNP format, therefore similar pointwise data are used for MCNP and WIMS calculations. The optimization algorithm evaluates the errors and generates the new energy structure.
3.1 Benchmarks and Evaluated Parameters
In the current study, four different H2O moderated UO2–PuO2 lattice problems which are proposed by WIMS Library Update Project (WLUP) for benchmarking purposes are selected. These include:
i) CRX facility: WCRX-PU1 [10]
ii) TCA facility: JTCA-PU1 [11]
iii) GE Experiment: GE_PU1 [12]
iv) BNW Experiment: BNW-PUa1 to BNW-PUd1 [13]
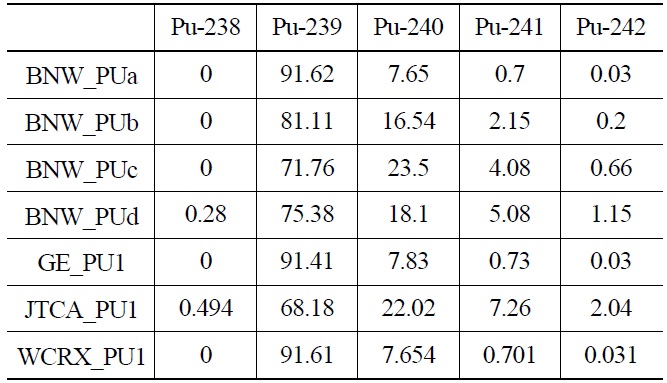
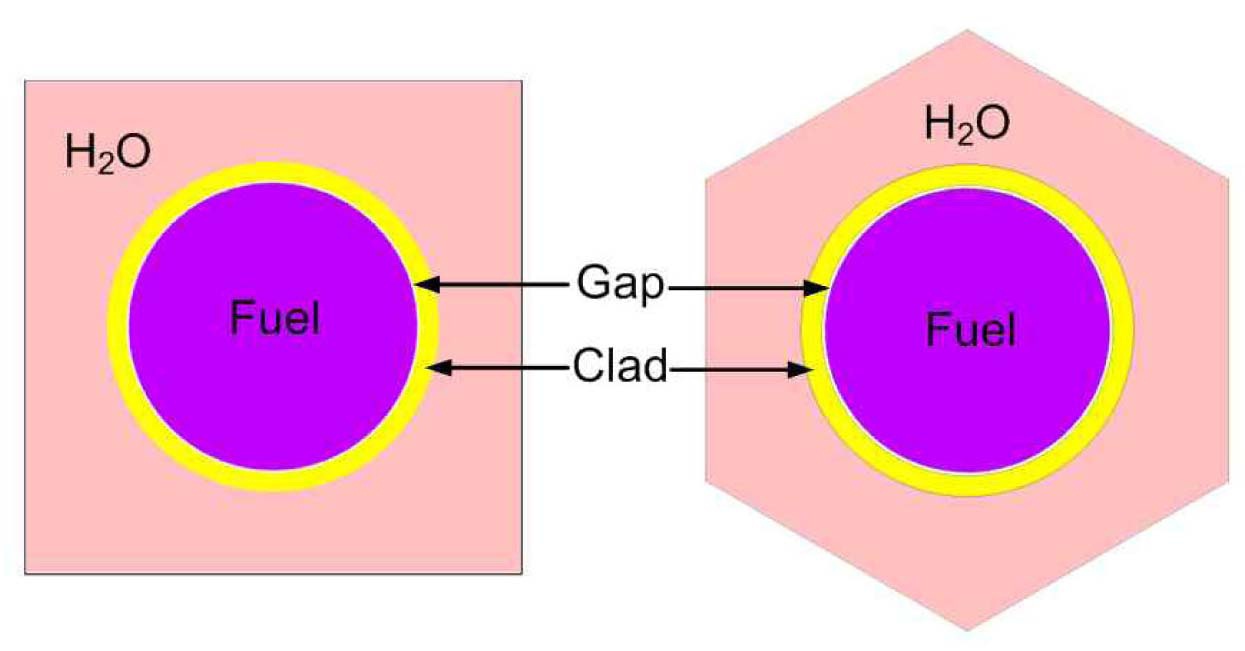
Each case is selected to be representative of the individual set. The general specifications of these benchmarks are summarized in Table 1. Also their PU isotopic composition is shown in Table 2. The geometrical representations of benchmark lattices are also depicted in Fig. 2.
The reactions of isotopes U-235 and U-238 at 293° K are calculated in benchmark lattices using WIMSD-5B code. To evaluate the accuracy of energy group structure the integral parameters are calculated and compared with the MCNP code results. These integral parameters include
[Table 2.] Pu isotopic Composition (wt%)
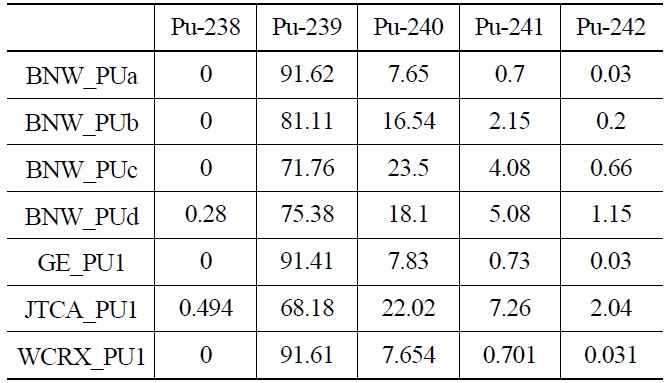
Pu isotopic Composition (wt%)
the infinite multiplication factor (K∞) and the following spectral indices [15] which are calculated with the thermal cutoff energy of 0.625 eV:
Due to the paucity of experimental data for spectral indices as well as the uncertainty in the measured multiplication factor, the MCNP code was used to evaluate the accuracy of the results. Using this approach, the error would just be originated from the selection of energy group structure. To model the benchmark lattices in the MCNP code, detailed geometrical specifications are required. Previous attempts [16,17] to model the similar lattices in MCNP have led to large discrepancies when compared to actual experiment results. These discrepancies have been attributed to the imprecise description of the whole core configuration. Due to these discrepancies, in this study the benchmark problems are modeled as 2-D pin cell with a periodic boundary condition to define an infinite system without leakage through the use of MCNP and WIMS codes. The results of continuous energy MCNP code are used for evaluation of the error of integral parameters caused by the selected energy group structure.
The NJOY code system is used for the generation of WIMS cross section library. Fifteen isotopes including fuel, clad, and moderator materials are processed using evaluated nuclear data files selected by WLUP. These data files are selected from different sources such as: JENDL-3.2, FOND2.2, CENDL-3, JEF-2.2 and ENDF/ B-VI.8 based on the results of analyses of more than 200 benchmark cases for different libraries [18].
The following modules of NJOY are used respectively for data processing.
Moder: used for format conversion.
Reconr: to reconstruct the resonances and prepare linearized pointwise cross sections
Broadr: to add the temperature dependence to the pointwise cross sections. The cross sections were processed for 293°K according to the benchmark problems.
Unresr: Unresolved resonance data processing to self shield the cross sections in the unresolved resonance energy range. This module is used for moderator and clad materials.
Purr: Unresolved resonance data processing for the resonant isotopes. Since Unresr module produces nonmonotonic self-shielding factors at moderately high dilutions [18], it is used only for moderator and clad materials. The Bondarenko background cross sections are chosen according to the dimensions and compositions at which the materials are likely to be used [18].
Thermr: Adds thermal scattering law to the processed tape. A free gas model is used for all materials except hydrogen. The data of H when bounded in H2O is used for processing the thermal scattering of hydrogen. Up to this point all the processes were on a unionized energy grid.
Groupr: This module averages the pointwise cross sections over the energy groups. It produces multi-group cross sections and group to group scattering matrix. Groupr uses a feed function C(E) to generate the weighting spectrum based on the Bondarenko or flux calculator model. C(E) is chosen as the typical LWR neutron spectrum as in WLUP files. For resonant isotopes, the flux calculator model is used to obtain the flux in homogenous mixture of resonant isotope with hydrogen from 0.1 eV up to the upper limit of the resolved resonance range. The Narrow Resonance approximation is used above this energy. For other materials the Bondarenko flux model is used.
Wimsr: Used to prepare the WIMS library format cross sections from the processed Group-wise Evaluated Nuclear Data File (GENDF) tape. The P1 scattering matrix is included in the output library for H and O materials. For other materials transport correction is applied on P0 cross sections (Total and In-group scattering) using the current spectrum generated by Groupr.
Acer: To convert the processed pointwise cross sections to MCNP library format
In addition, the WILLIE program [18] was used to make the library starter file and integrate the processed data in the new library. The accuracy of the processing procedure is verified against the WLUP results for different benchmarks.
3.3. Particle Swarm Optimization
Eberhart and Kennedy (1995) proposed the Particle Swarm Optimizer (PSO) algorithm [7], a simple but effective evolutionary algorithm, motivated from the simulation of birds’ social behavior. With the advantages of computing with real numbers and the need for only a few parameters requiring adjustment, the PSO algorithm has been applied to many fields. Moreover, its application in many kinds of scientific research fields shows its valuable properties and practicality. PSO, as an optimization tool, provides a population-based search procedure in which agents (individuals) called particles change their positions with time. In PSO, a set of randomly generated solutions propagates in the design space towards the optimal solution over a number of iterations based on large amounts of information about the design space that is assimilated and shared by all members of the swarm. The new position of the particle is determined by the sum of its current position and the velocity [19]. At each time step (iteration) a particle updates its position and velocity by the following equations:
Where,
where
3.3.1 Mapping of the Energy Group Structure Optimization Problem on the PSO
In present work, PSO is mapped, compared and used for the energy-group structure optimization problem. The convergence criterion of the PSO is assigned by a maximum iteration number. In our study case, there are 69 meshes in each energy group structure. A straightforward method of energy-group structure representation can be established using a 1×d position vector,
Thus, in this study the length of each position vector is considered as 69. The characteristics c1 and c2 which are respectively, the coefficients of individual and social learning of the particles were adjusted so that c1+c2=4.
In addition, the value of the
In this study, the position of a particle represents a candidate solution (candidate energy group structure) to the optimization problem at hand. The behavior of a particle is determined by its fitness, which is evaluated through calculation of a fitness (objective) function relative to the problem to be solved at its current position. Thus, we need to define the objective function to evaluate each particle (energy group structure). A structure which improves the results in all benchmark cases is favorable, however to minimize the number of parameters in objective function just two different cases, BNW_PUa1 and JTCA_PU1, were selected. The fitness function (FF) is defined as follow:
Where,
Other parameters are repeated for JTCA-PU1with relevant weights.
For more emphasize on the multiplication factor, the weights are selected as: W1=W3=2 and W2=W4=1.
It should be noted that in each step after the generation of a new particle position (see Fig. 1 flowchart), we must sort its elements in order to use it in NJOY code input.
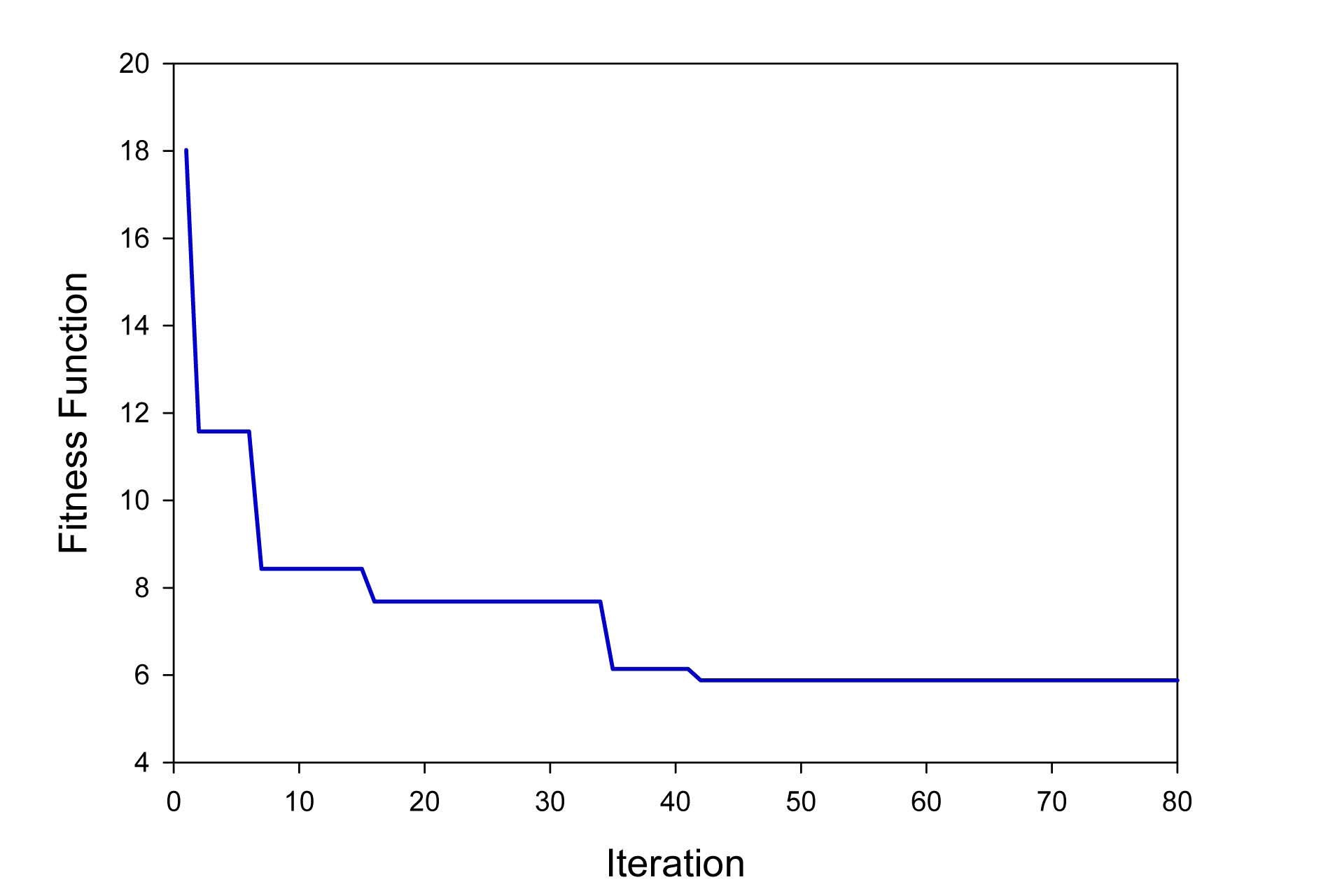
The main goal of this investigation is to minimize the value of the objective function (Eq. (8)) as much as possible using the PSO method. Fig. 3 illustrates the fitness function value in different iterations. As it can be seen, the fitness value decreases rapidly from 18.01 to 5.88 and the calculation converges after 41 iterations.
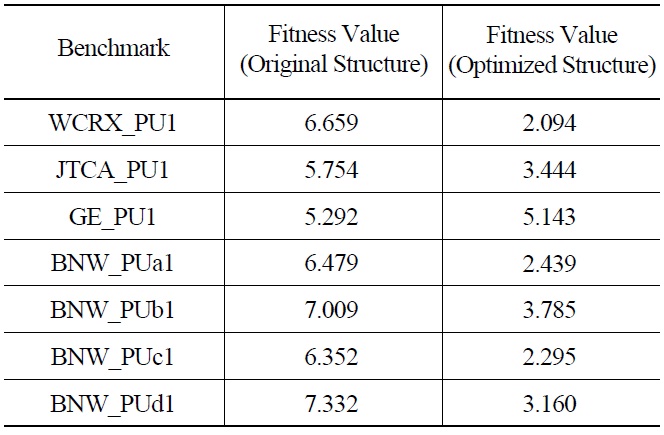
The optimal energy structure has been used to solve other benchmark problems. The comparison of fitness function values for different problems using original and optimal energy structures are shown in Table 3. The fitness function has decreased in all the benchmark problems.
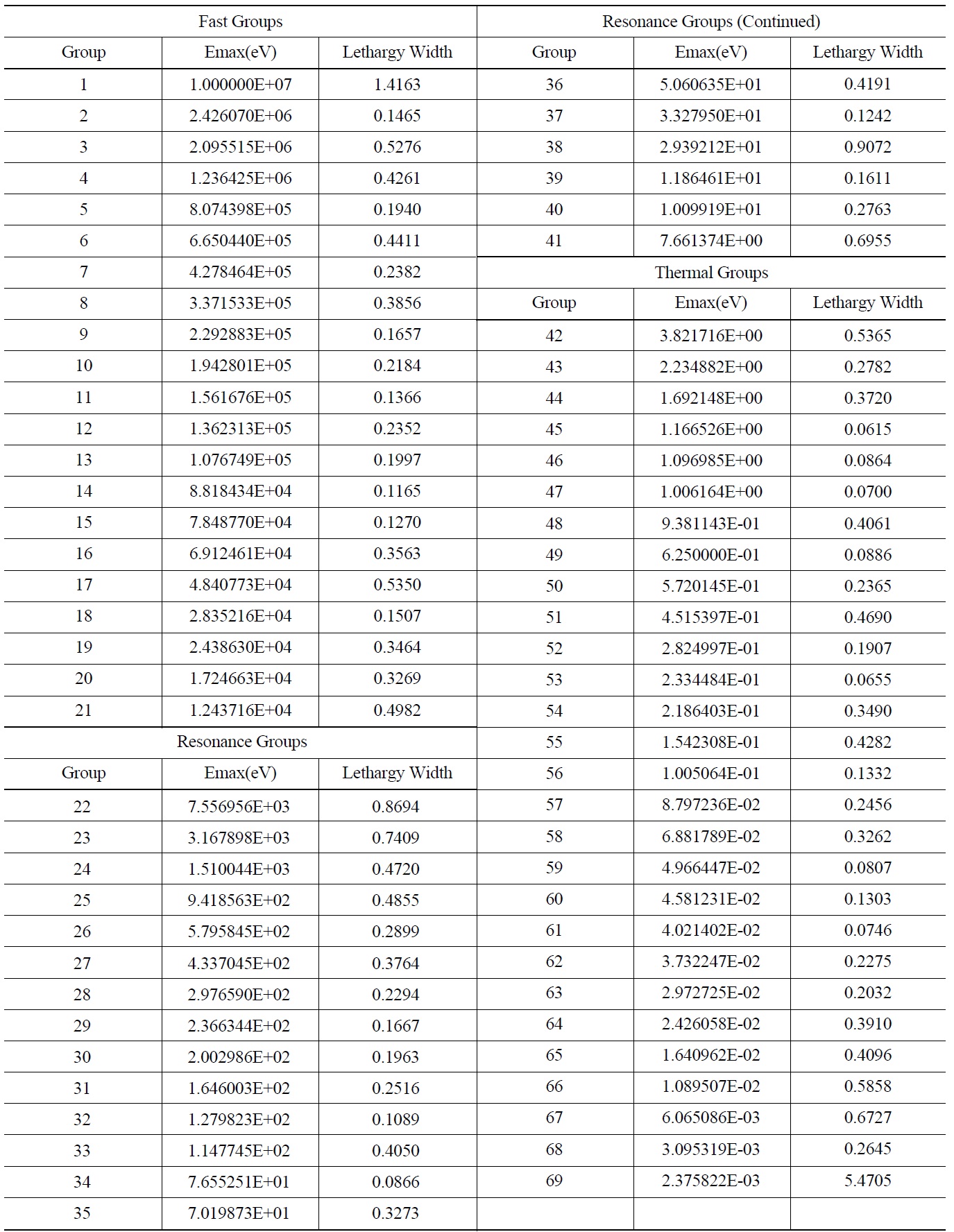
Table 4 represents the optimal structure with the lowest fitness proposed in this paper using PSO for the test cases described in section 3.1.
The optimization has led to 21 fast groups with energies greater than 9.118 keV, 20 resonance groups and 28 thermal groups with energies lower than 4 eV. These values are the conventional boundaries for three different energy regions. Similar to the original structure, most energy groups are selected in the thermal region by the optimization process.
[Table 3.] Fitness Function Value for Benchmark Problems
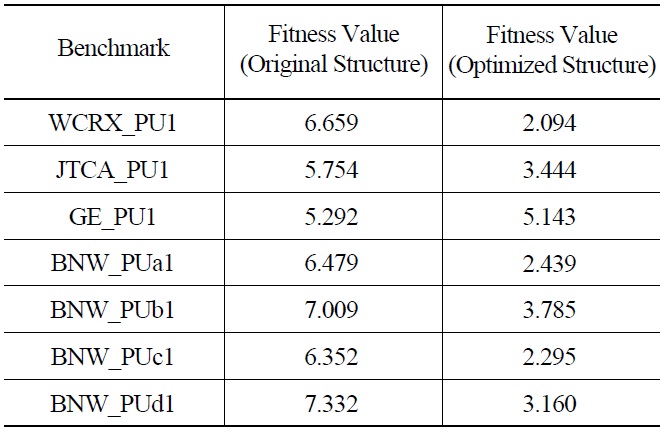
Fitness Function Value for Benchmark Problems
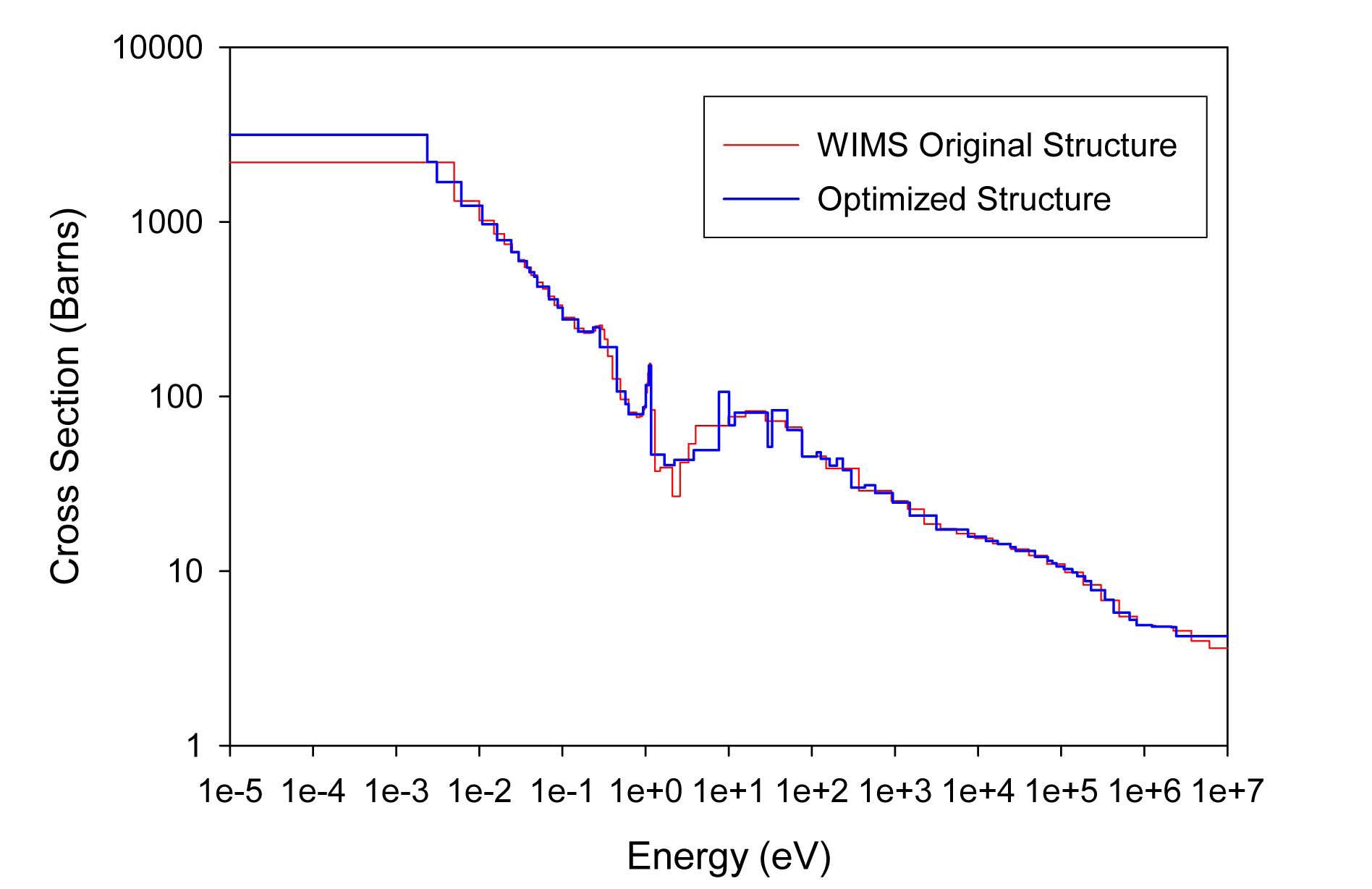
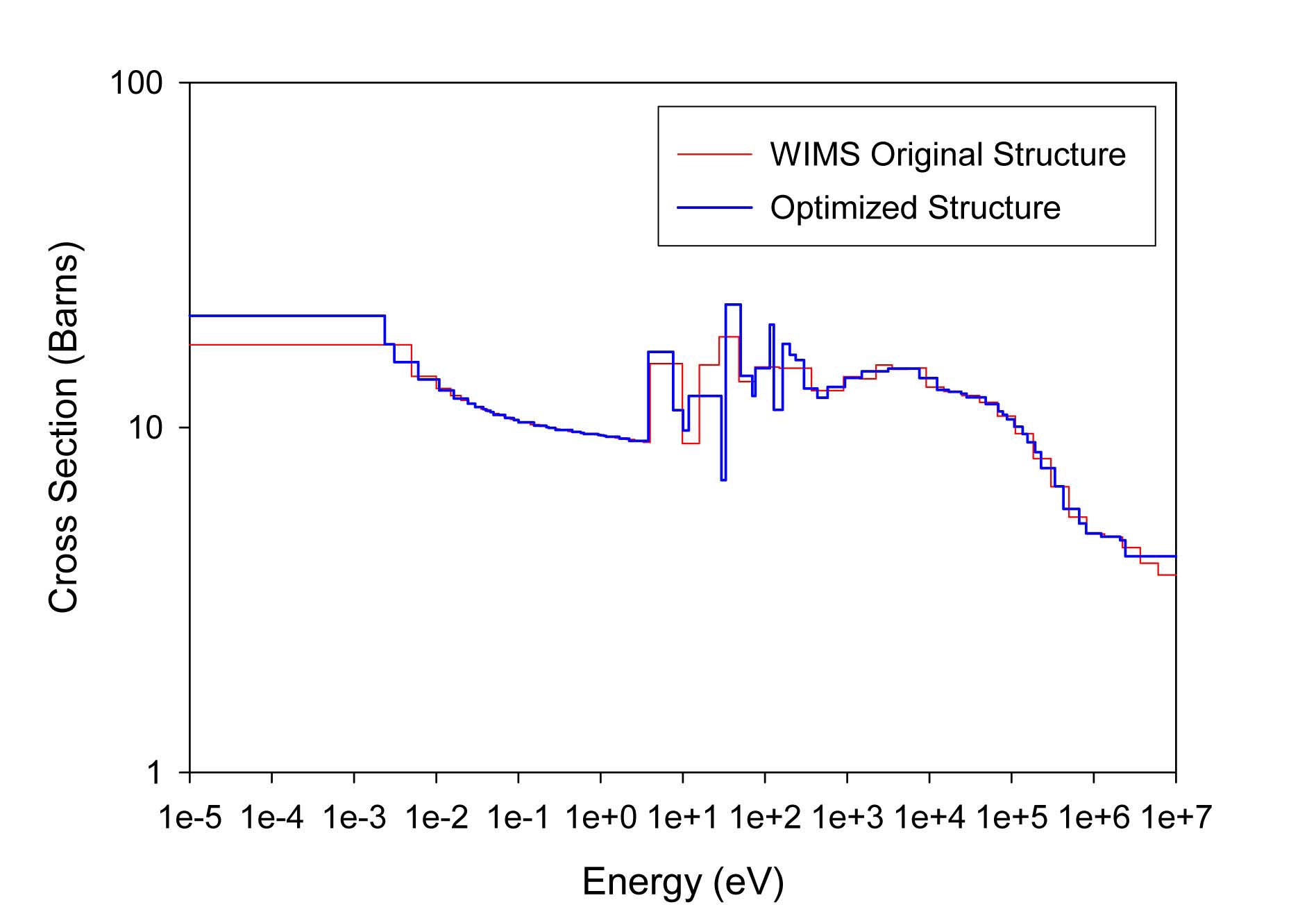
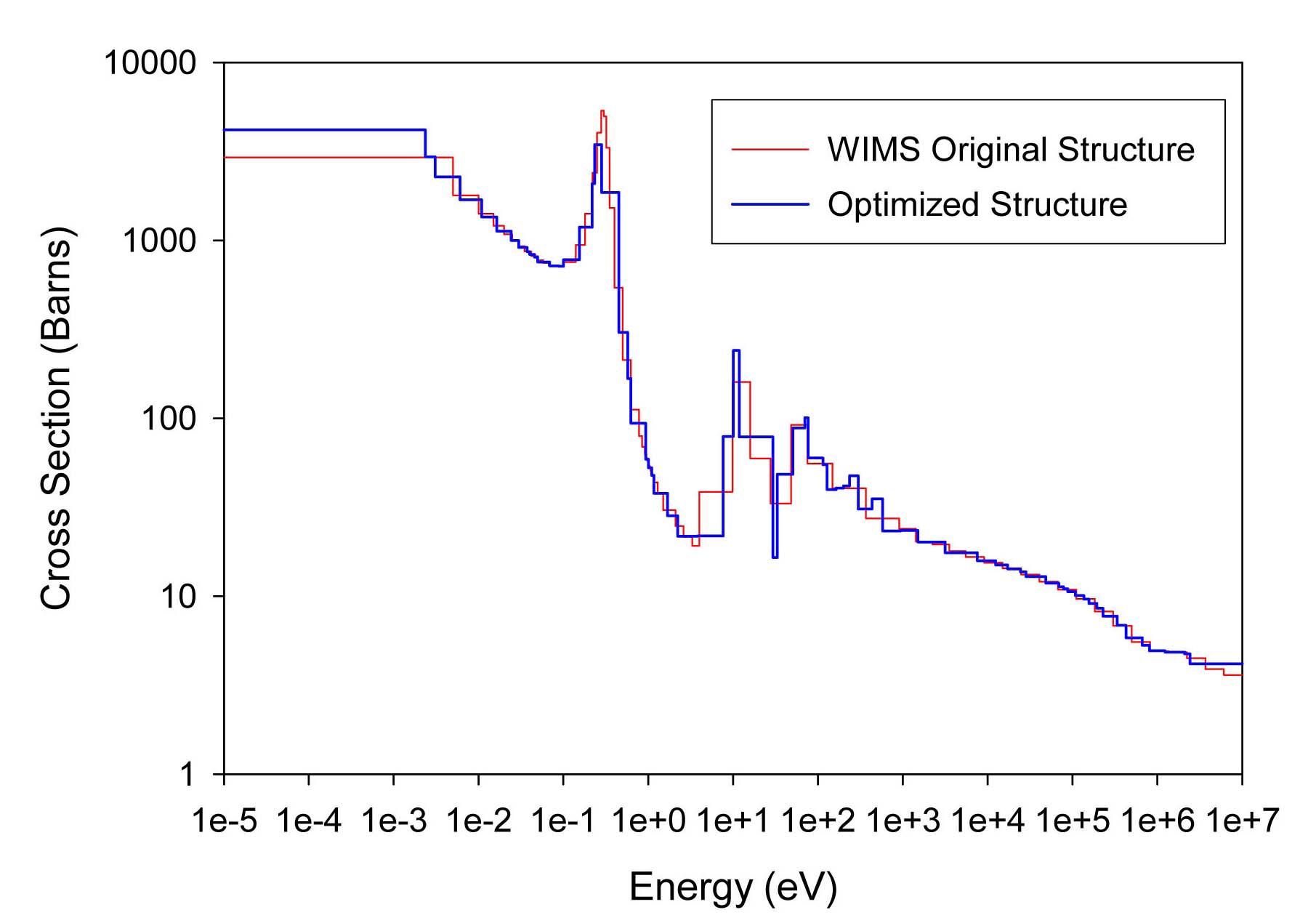
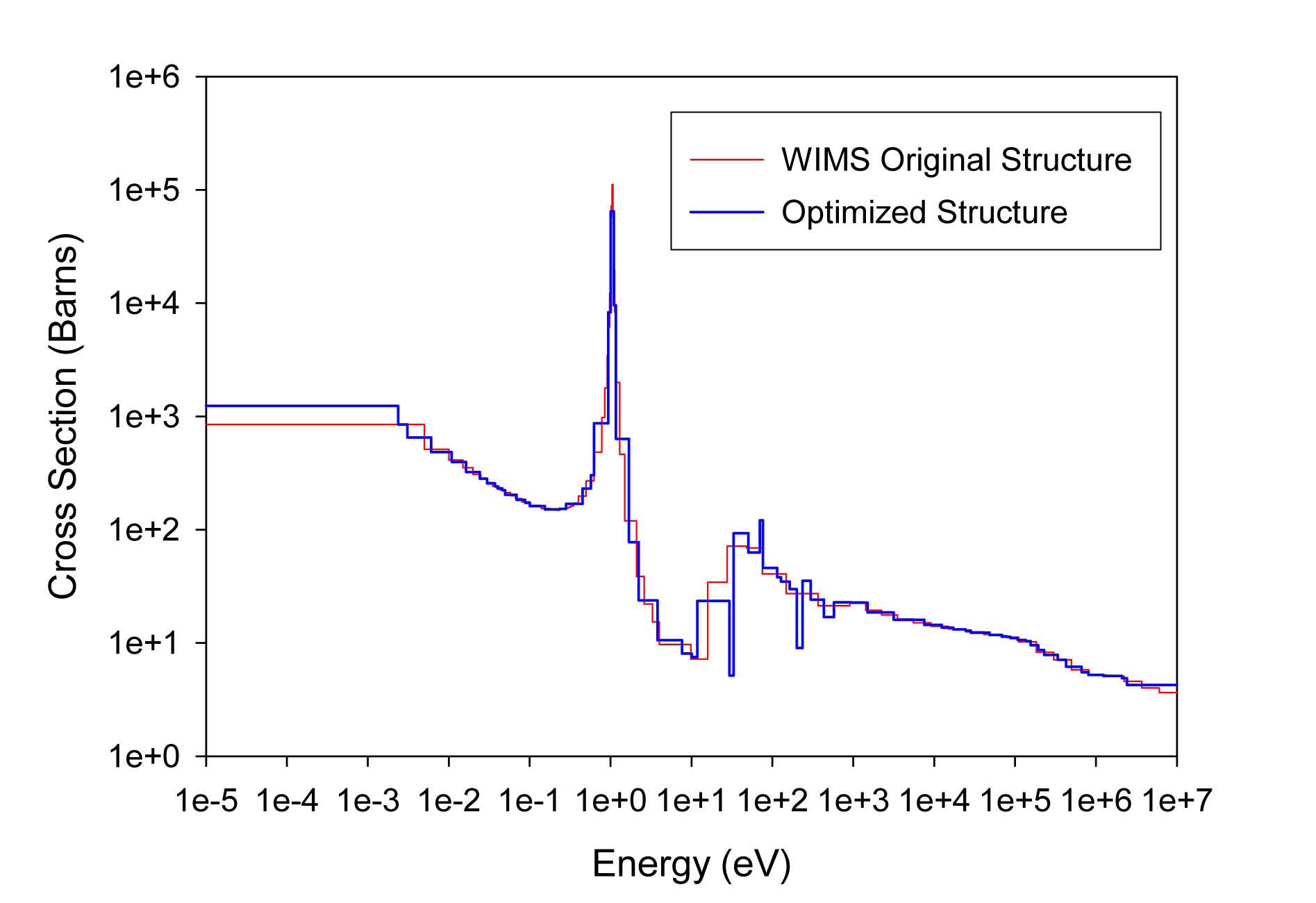
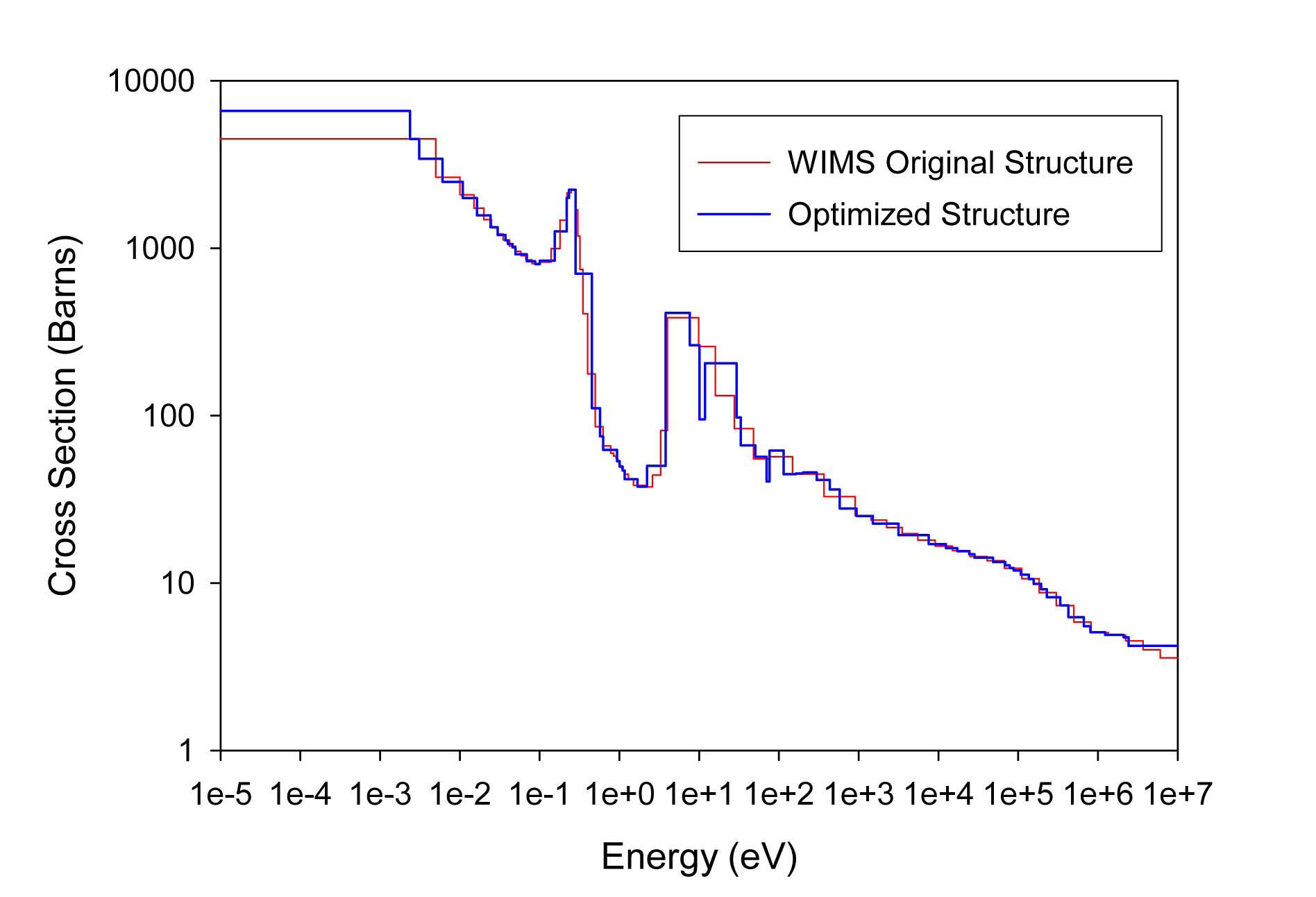
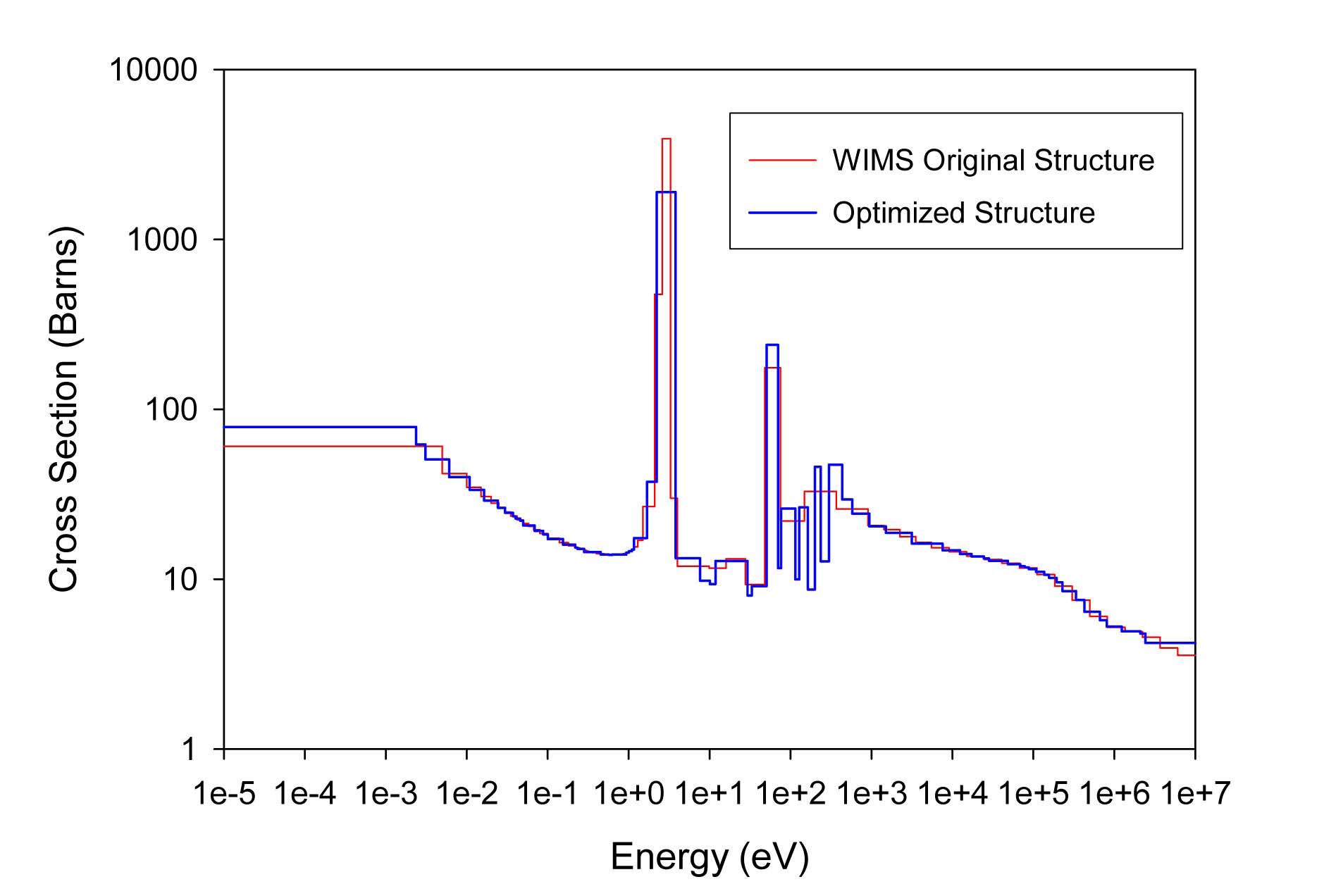
The total cross sections of PU isotopes under the original WIMS and the optimized energy structures are illustrated in Figs. 4-9. As can be seen from these figures, in resonance energy range the optimization algorithm has selected the groups according to the resonances of fuel material. As we know, to select the proper energy structure, complicated phenomena in the reactor are taken in to
[Table 4.] The proposed 69 Group WIMS Energy Group Structure for MOX Thermal Lattices
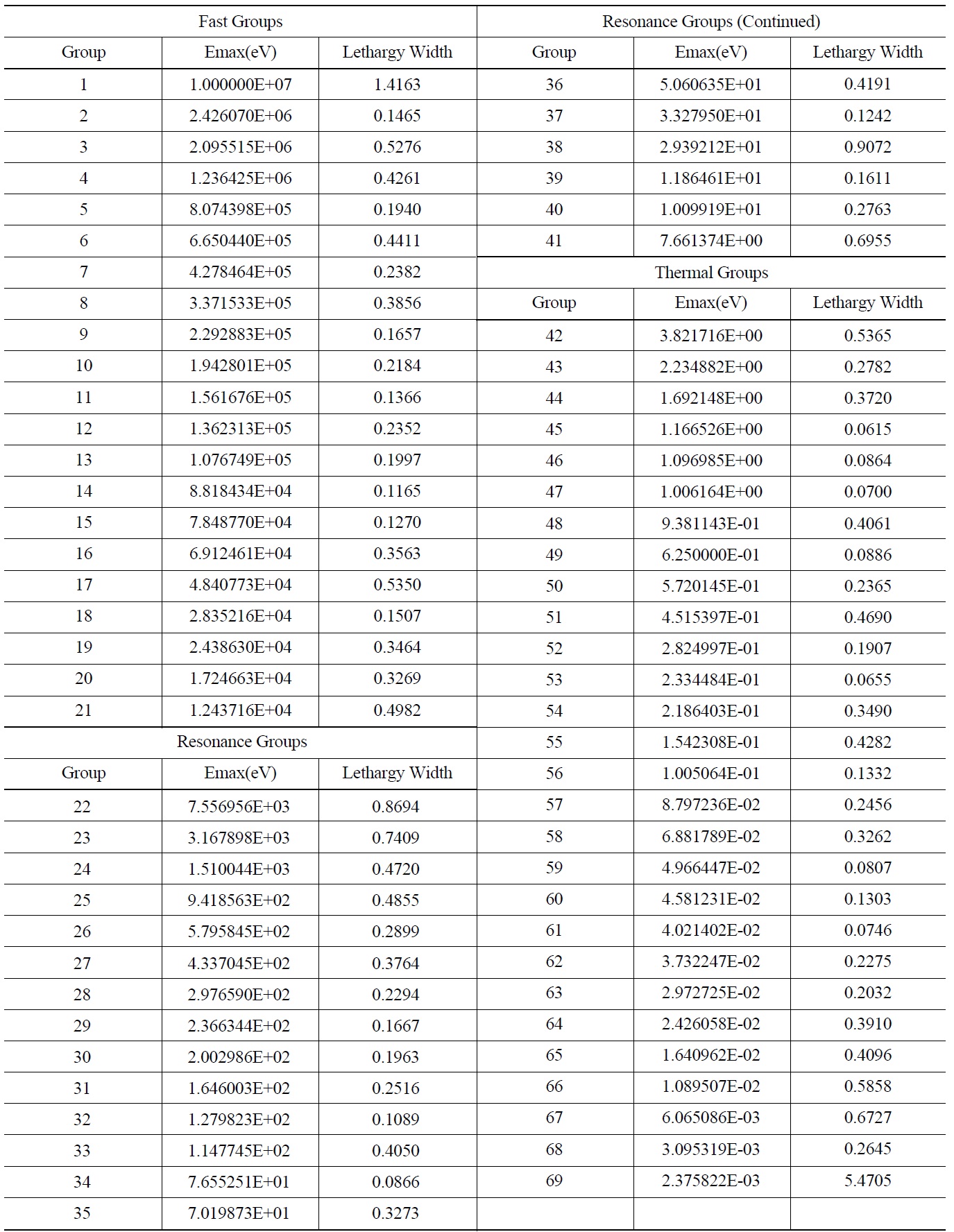
The proposed 69 Group WIMS Energy Group Structure for MOX Thermal Lattices
account; however by employing this heuristic method, such considerations are automatically incorporated in the selection of energy structure.
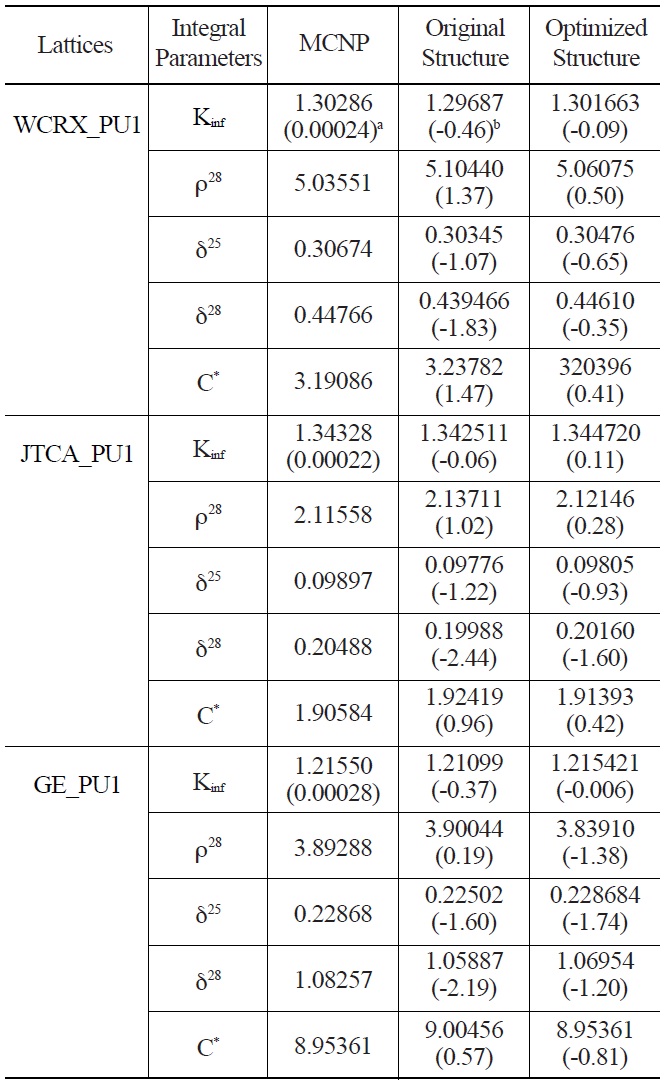
The infinite multiplication factor and spectral indices obtained from the generated library with the optimized
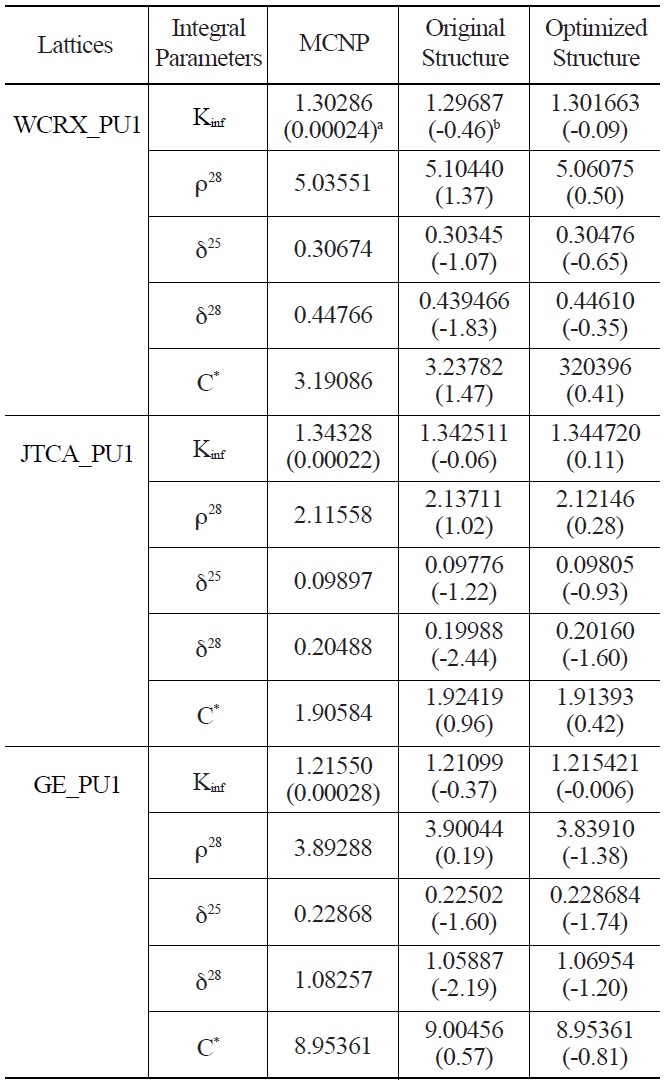
Comparison of Calculated Integral Parameters for WCRX, JTCA and GE Benchmarks using Original and Optimized Energy Structures
energy group structure are shown in Tables 5 and 6. The results of the original WIMS library are also listed. As can be seen from the results, except the multiplication factor of JTCA_PU1 and two spectral indices of GE_PU1, other parameters are improved considerably.
The energy group structure of WIMS code was studied in this paper. A calculation system was prepared to generate the WIMS 69 group library based on the input energy structure using the NJOY code system and also to calculate integral parameters using WIMSD-5B code. The PSO
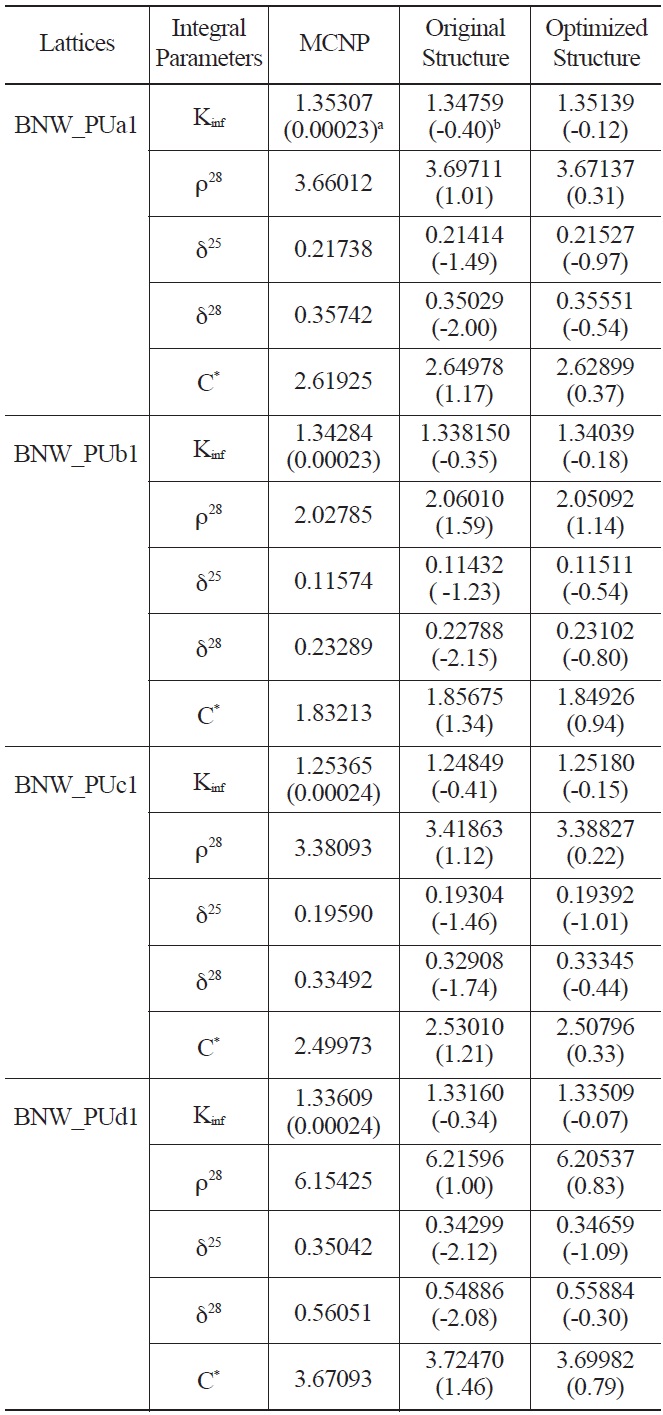
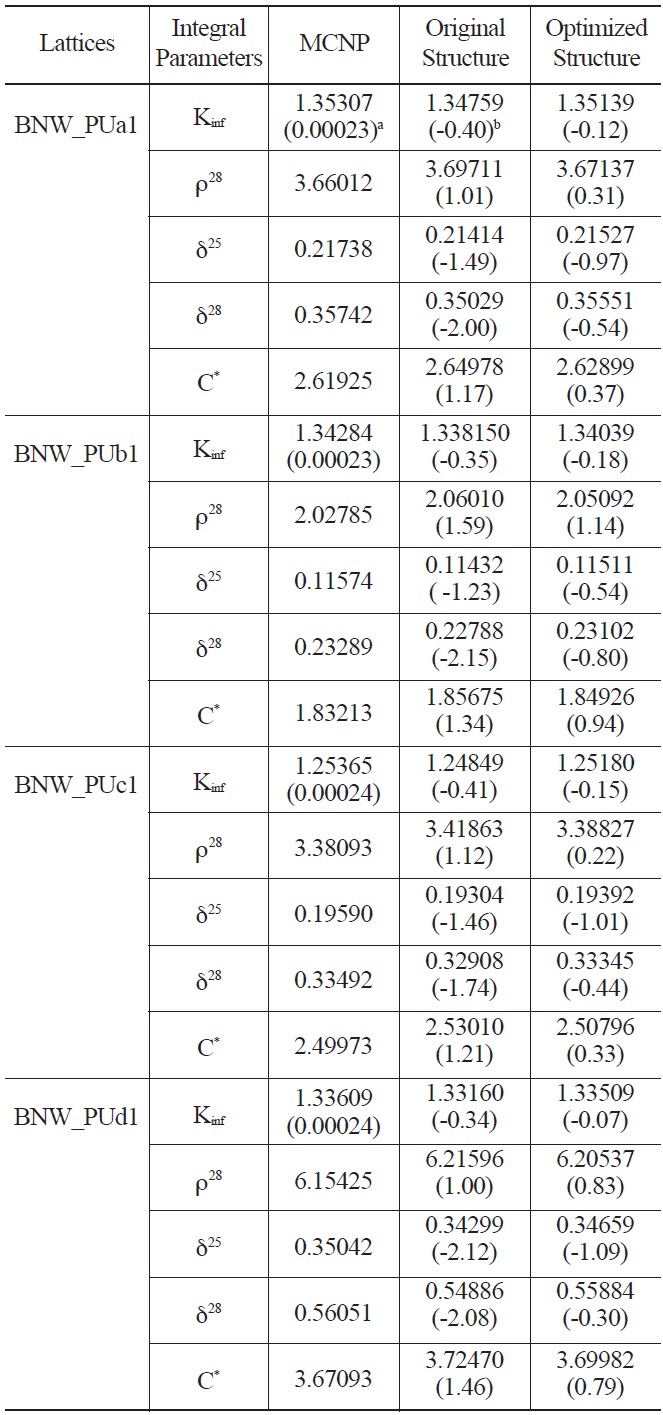
Comparison of Calculated Integral Parameters for BNW Benchmarks using Original and Optimized Energy Structure
optimization method was applied for the selection of energy boundaries. The error of multiplication factor and spectral indices in four categories of MOX thermal lattices were analyzed for this purpose. An optimal energy structure with the lowest fitness value has been proposed. The results show that using the optimal energy structure leads to more accurate spectral indices and multiplication factor in MOX thermal lattices in most cases.
By using this methodology, one can increase the efficiency of multigroup transport calculations employing the optimized energy structure. Such calculations lead to more accurate results with lower number of energy groups.