Sensitivity coefficients are utilized in the three fields; sensitivity analysis, uncertainty estimation and cross section adjustment. In the sensitivity analysis, the effect of cross section changes, for example from JENDL 3.3 to 4.0, on core characteristics is estimated by calculating the product of sensitivity coefficients and cross section changes, which is important in releasing a new cross section library. In the uncertainty estimation, the prediction uncertainty is evaluated by using the cross section covariance and the sensitivity coefficients1. In the cross section adjustment, the sensitivity coefficients play an important role in adjusting the cross sections by using the measured neutronics characteristics based on the Bayes theory. Thus in these three applications, the sensitivity coefficients have important roles, and accurate evaluation is necessary.
Sensitivity coefficients are usually calculated by using the generalized perturbation theory because the calculation requires a lot of computing time. Sensitivity coefficients of individual core characteristics such as keff, power distribution and control rod worth are calculated relative to cross section changes of each reaction type (fission, capture, scattering) for many energy groups. The generalized perturbation theory shortens the computing time by the use of generalized flux and generalized adjoint flux. TSUNAMI module2 in SCALE code is a representative sensitivity calculation code. In Japan we have developed SAGEP3, SAGEP-T4 and SAINT5 codes based on the generalized perturbation theory with use of the diffusion theory, transport Sn method, and collision probability method, respectively.
However, the sensitivity coefficients are usually calculated by changing the effective cross sections. The effective cross sections are the product of the infinite- dilution cross sections and the self-shielding factors. The self-shielding factor varies with other cross section changes due to change of the background cross section, and the interaction effect has to be considered in estimating the sensitivities.
The purpose of this paper is to derive a new method to calculate the sensitivity which shows the core characteristic changes due to the change of the infinite dilution cross sections. The present method introduces a correction TERM to the conventional sensitivity coefficient. Therefore, the conventional approximation utilized hitherto with this correction TERM can be used to calculate the improved sensitivities.
To check the accuracy of the present method, numerical calculations are performed for a representative PWR cell model. Approximated (conventional) sensitivity coefficients are calculated by using the SAINT code, which can treat cell geometry using the collision probability method, and then the improved sensitivity coefficients are calculated by using the present method. Finally the improved and approximated sensitivity coefficients are compared with a reference one calculated by MCNP code.
The paper is organized as follow: The relation between improved and approximate sensitivity coefficients is derived in Section II, and numerical results are shown in Sec. III. Section IV summarizes the conclusion.
Core characteristics such as keff, power distribution and control rod worth are calculated by using an effective cross section in deterministic methods. Usually the effective cross sections are calculated by using the Bondarenko selfshielding factor method1, the subgroup method1 et al. Here the Bondarenko self-shielding factor method has been used. With that method the effective cross sections are expressed by the infinite dilution cross section and the self-shielding factors ? 6:
The self-shielding factors depend on the background cross section and temperature. The background cross section for nuclide i` in a homogeneous medium is calculated with the formula
where Nk is the atomic number density of light nuclide k and σkt is the microscopic total cross section. In a heterogeneous medium the background cross section for the infinite regular lattice is given by
where C is the Dancoff factor, Σe is the reciprocal of the fuel diameter, a is the Bell factor, and σbi` is the background cross defined by Eq. (2).
The sensitivity coefficient is defined by the relative change of the core characteristics due to the relative change of the cross section. Here we consider the following two sensitivities, the sensitivity due to the relative change of the infinite dilution cross sections and the approximate sensitivity due to the relative change of the effective cross sections
and
The relative change of the infinite dilution cross sections causes the change of the core characteristics as follows:
From Eq. (1), one can obtain
Therefore, the improved sensitivity is expressed by using the approximate sensitivity as follows:
Let us consider the above equation in more detail. The sensitivities and the cross sections are dependent on nuclides, reaction types (such as fission, capture and scattering) and energy groups. Let us consider the case where there is a perturbation in
The sensitivity for the nuclide i, reaction type j in energy group g is given by
The first term is the direct contribution to S, which can be calculated using the conventional tools evaluating sensitivity coefficients such as SAGEP, SAGEP-T and SAINT. The second term represents the indirect contribution through the change of self-shielding factor. These coefficients can be calculated as follow:
Here we assume that the wide resonance approximation is applied for heavy nuclides, of-course the narrow resonant approximation is applied for light nuclides. The self-shielding effect depends on the neutron spectrum, where the neutron spectrum for the heavy nuclide i` is written as
Equation (10) indicates that when σai`(E) and σbi` change by the same factor, the neutron spectrum remains the same, This shows that the ratio
Now let us consider a case when there are cross section perturbations in σ
When the perturbations of cross sections Δσ = σ` - σ are small compared to σ, so h` can be written as
Equation (11) is interesting, for when the relative changes of Δσ`bi`/σ`bi` and Δσ`ai`(E)/σ`ai`(E) are the same, h`= h, and therefore the self-shielding effect remains the same before perturbation.
The self-shielding effect is dependent on the ratio of σb to σa, so the perturbed self-shielding factor can be written as:
Using Eq. (11), Eq. (12) reduces to
When there are some heavy resonant nuclides mixed in fuel (indicated by i and i`), the neutron spectrum in Eq. (10) is replaced by
From Eq. (14) the total background cross section is
Therefore the change in the background cross section due to the cross section perturbation of heavy nuclides i is
because Δσi`b0 = 0 for these heavy nuclides.
Substituting Eq. (16) to Eq. (13), the change of the self-shielding factor of nuclide i`, reaction j` due to the cross section perturbation of nuclide i, reaction j will be written as
where δii`=1 for i=i`, and =0 for i≠i`.
Therefore we obtain:
where dσia/dσij is usually unity except for scattering reaction;, in which case it is zero.
Usually the ? table is described as a function of the background cross section only or a relevant nuclide, and the total cross section is assumed to be fixed in these tables, therefore ∂f
∂f/∂
of Eq. (9) is called TERM and can be written as
When one considers the cross section perturbation of light nuclides k, the narrow resonance approximation has to be used. In this case;, the neutron spectrum is expressed by
and therefore σa is replaced by σt in Eq. (20).
The SRAC7, SAINT and MCNP8 codes are used to perform these analyses, where the SRAC code is used for the self-shielding factor calculations, the SAINT code for conventional sensitivity coefficient calculations and the MCNP code for verification. In all calculations, the ENDF/B-VI library was used.
Sensitivities are calculated for the standard PWR ?UOX fueled pin-cell. The fuel, clad and water properties are shown in Table 1.
[Table 1.] Isotopic Data for UOX Cell
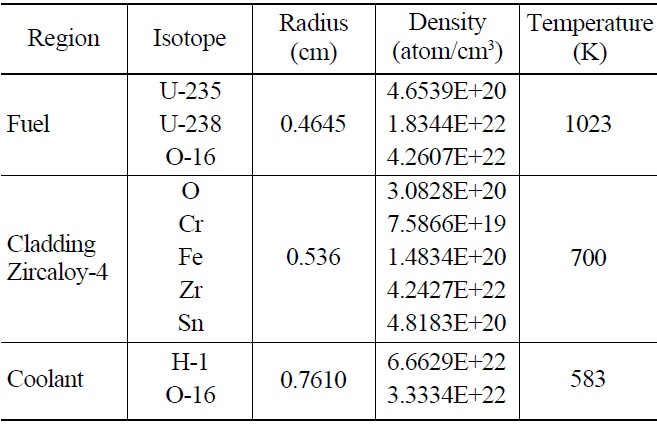
Isotopic Data for UOX Cell
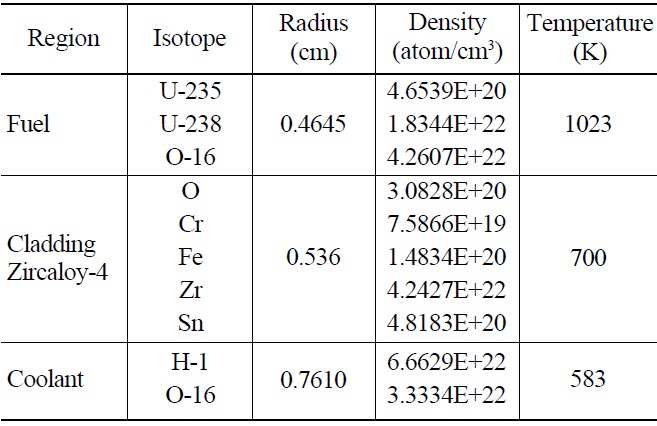
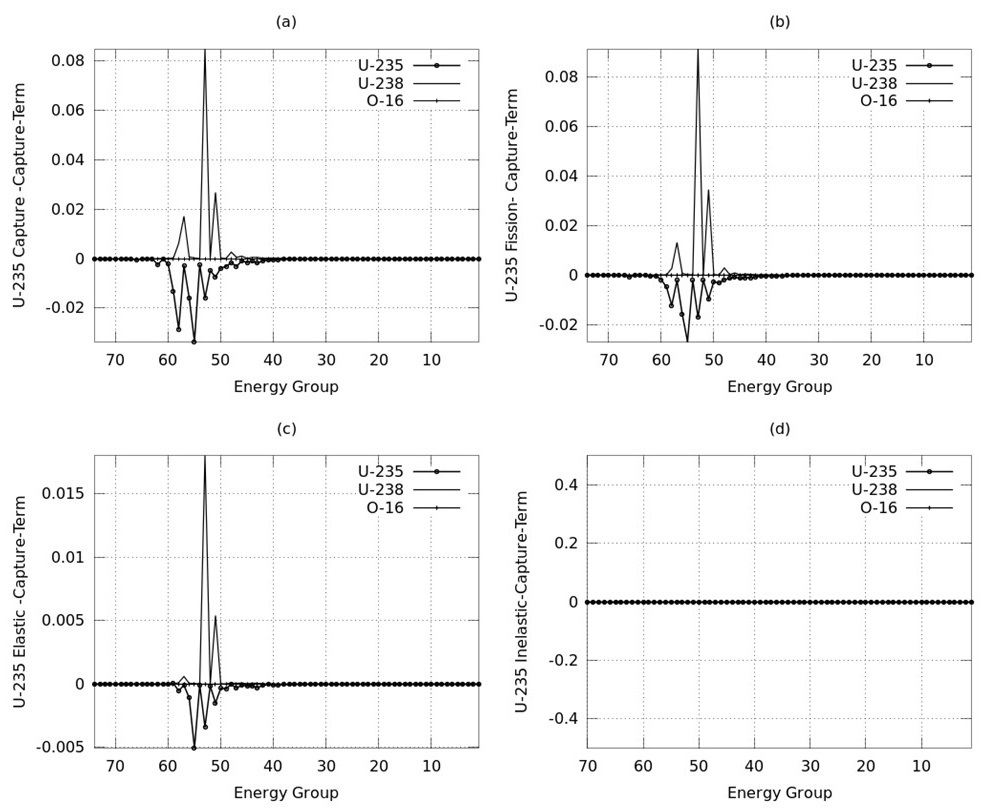
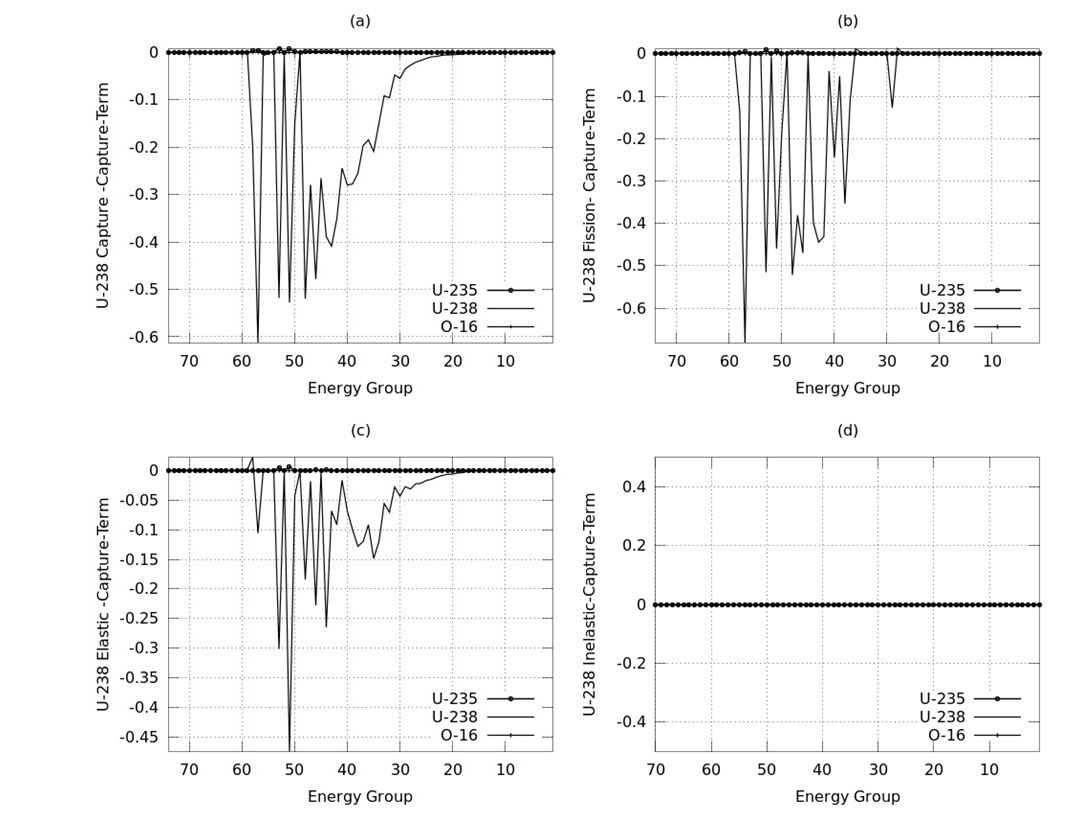
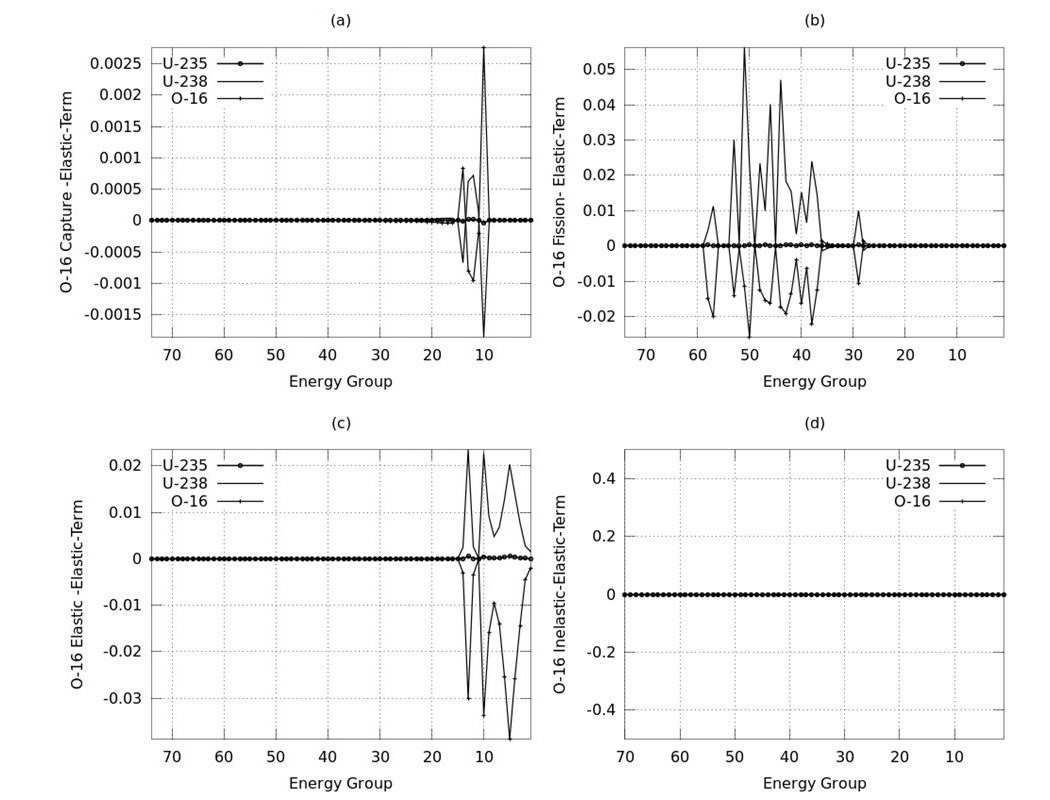
First, the self-shielding factors are calculated using the SRAC2006 code for different isotopes and reactions. Then the self-shielding gradients with respect to the background cross section are calculated, and from Eq. (20), the TERMs are determined. TERMs are shown in Fig. 1~ 4 as a function of energy groups (10 MeV ~ 4.1399E-01 eV).
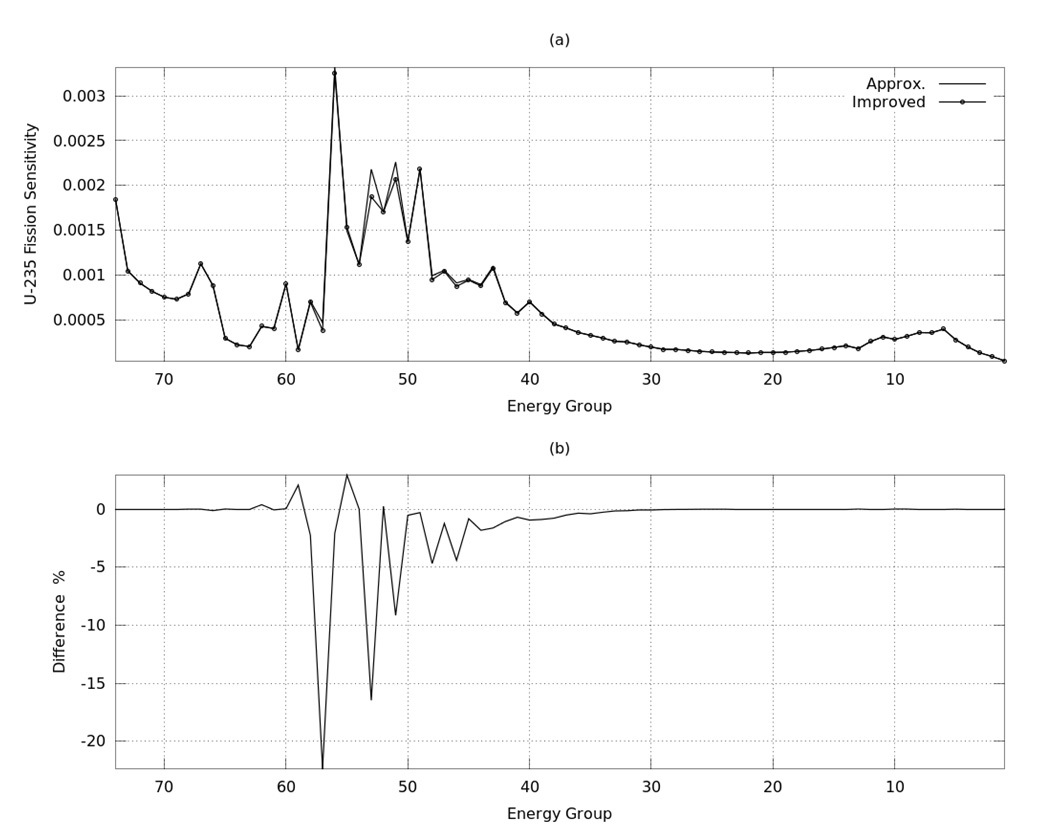
The TERMs in Figures 1(a), (b), (c) and (d) represent the changes of U-235 capture, fission, elastic and inelastic self-shielding factors respectively due to perturbations in U-235, U238 and O-16 capture cross sections.
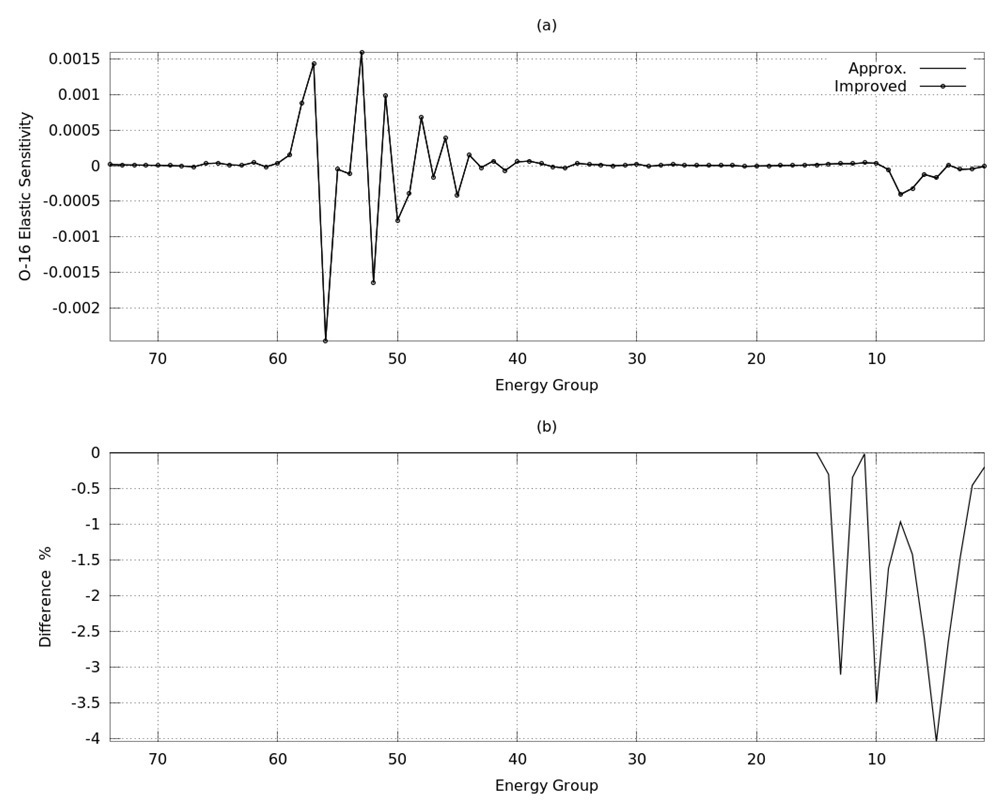
Figures 2~ 4 represent the changes of U-238, U-235 and O-16 self-shielding factor due to perturbations in capture, fission and elastic cross sections respectively.
The SAINT code is then used to calculate the conventional approximated keff sensitivity coefficients for different isotopes and reactions. After calculating the approximated sensitivities and the TERMs, the improved
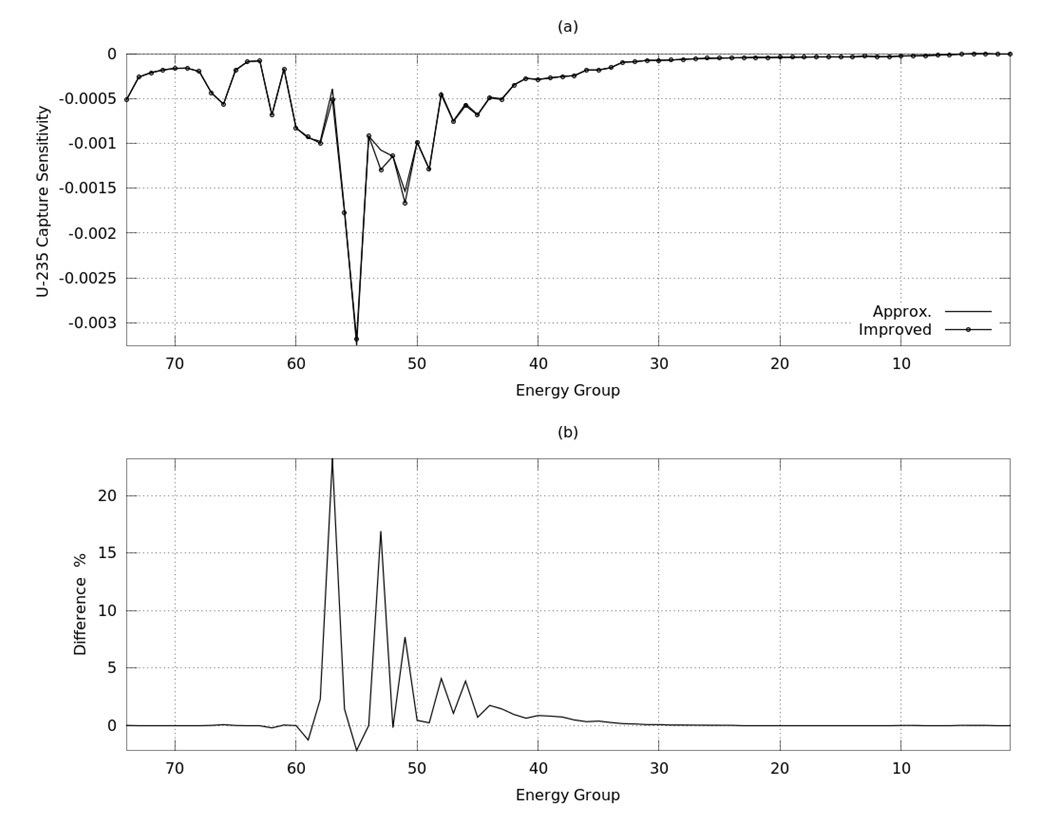
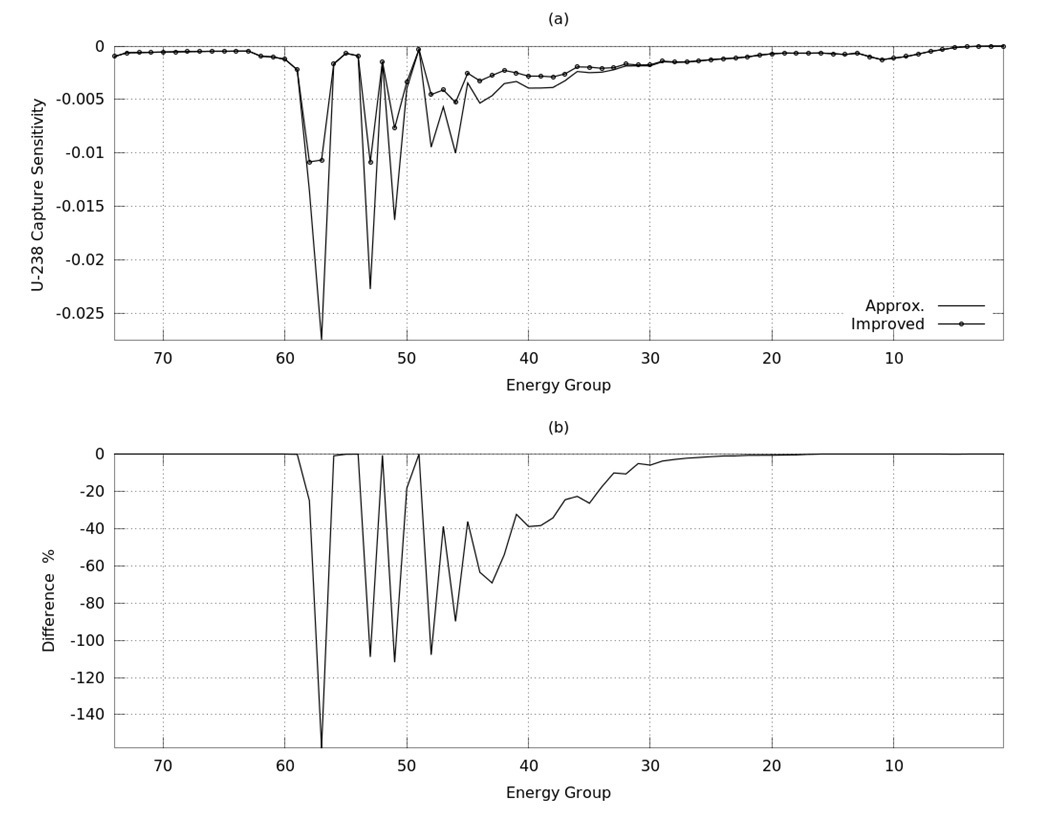
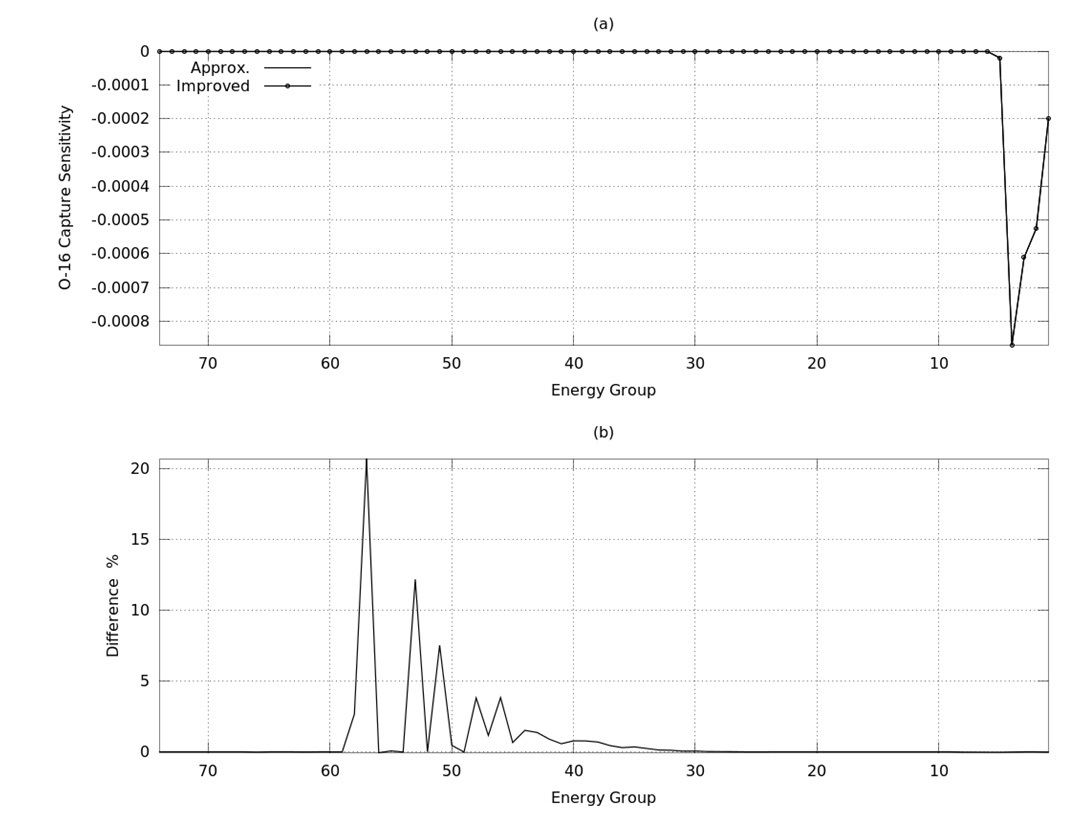
keff sensitivities can be calculated using Eq. (9). Figures 5~7 represent the approximated and improved keff sensitivities for U-235, U-238 and O-16 capture cross sections respectively, while Figures 8,9 represent keff sensitivities for U-235 fission and O-16 elastic cross sections respectively. Figures (a)’s stand for the sensitivity and (b)’s for the differences between approximated and improved sensitivity, where the difference is defined by:
Difference = (SImproved ? SApprox.)/SImproved x 100 (%)
It is shown in Figures 5~9 that the differences between improved and approximated sensitivities are large, at 57 (6.4759 - 8.3153 eV), 53 (1.7604E+01 - 2.2603E+01 eV) and 51 (2.9023E+01 - 3.7266E+01 eV) energy groups, which are the resonant energy groups, and the main contributor to these differences is the U-238 capture cross section.
MCNP5 calculations9 are performed at these energy groups in order to verify the present formula. The results of MCNP keff sensitivity coefficients compared to SAINT (Approximated) and improved sensitivity coefficients are shown in Tables 2, 3 for U-235 Capture and U238-Capture reactions respectively.
where
Eg is the energy group
[Table 2.] keff Sensitivity for U-235 Capture Cross Section

keff Sensitivity for U-235 Capture Cross Section
[Table 3.] keff Sensitivity for U-238 Capture Cross Section

keff Sensitivity for U-238 Capture Cross Section
It can be shown from these tables that Δ2 is smaller than Δ1, which means that the sensitivity calculated by the present model is more accurate and can be used to calculate the sensitivity coefficients.
In order to calculate sensitivity coefficients of neutronics characteristics relative to infinite dilution cross sections, a new formula was introduced. This formula can calculate the sensitivity coefficients using the conventional sensitivity coefficients and the correction term called TERM.
Using the present formula, one can easily revise the conventional sensitivity calculation codes such as SAGEP, SAGEP-T and SAINT.
The present formula has been verified by performing numerical calculations in cell geometry and comparing the results with the reference MCNP code.
The results calculated by the present formula were in good agreement with the reference results, particularly in the resonance energy groups. This agreement shows the usefulness of the present formula, and show the importance of self-shielding factors when calculating sensitivity coefficients in light water reactors.
is achievable.
I=log(1+ρ|hDS|2 + ρ|hDR|2),
which is the same as that of a 2×1 MISO system with the input covariance matrix
under the quasi-static channel assumption
I=log(1+ρ|hDS|2),