Blast waves driven by supernova (SN) explosions are presumed to accelerate cosmic rays (CRs) at least to the first knee of 1015.3 eV and possibly up to the second knee of 1017.5 eV. Moreover, in terms of energy budget, Galactic SN luminosity, LSN ? 1042 erg s-1, is powerful enough to replenish escaping cosmic rays with a luminosity of LCR ? 1041 erg s-1 (Blanford & Eichler 1987, Reynolds 2008). Time-dependent, diffusive shock acceleration (DSA) simulations of the CR acceleration at supernova remnants (SNRs) have demonstrated that an order of 10% of the SN explosion energy can be transferred to CRs, if a fraction ? 10-4 of incoming thermal particles are injected into the CR population at the forward shock (e.g., Berezhko et al 2009, Kang 2010).
In DSA theory, CR particles are scattered by magnetohydrodynamic (MHD) fluctuations (plasma waves) and gain energy through multiple crossings of the shock (Bell 1978, Drury 1983). Some suprathermal particles with velocities large enough to swim against the downstream MHD turbulence can return across the shock and get injected into the Fermi process (Malkov & Drury 2001, Kang et al. 2002). Then those streaming CRs excite resonant Alfven waves via two-stream instability and nonresonant waves via CR current-driven instability, which in turn amplify turbulent magnetic fields in the preshock region (Bell 1978, Lucek & Bell 2000, Bell 2004). Furthermore, magnetic fluctuations on scales larger than the CR gyroradius can grow in the presence of short-scale, circularly-polarized Alfven waves (Bykov et al. 2011, Rogachevskii et al. 2012) and through the firehose, filamentation, and acoustic instabilities (see Schure et al. 2012 for a review). Amplification of turbulent magnetic fields via plasma instabilities and injection of CRs via wave-particle interactions are regarded as integral ingredients of DSA at collisonless shocks.
X-ray observations of thin rims at the forward shock of several SNRs can be explained by the acceleration of ~10-100 TeV electrons, which cool radiatively in several 100 μG magnetic fields (e.g., Bamba et al 2003, Parizot et al. 2006, Reynolds et al 2012). This provides convincing evidence for efficient magnetic field amplification at strong CR modified
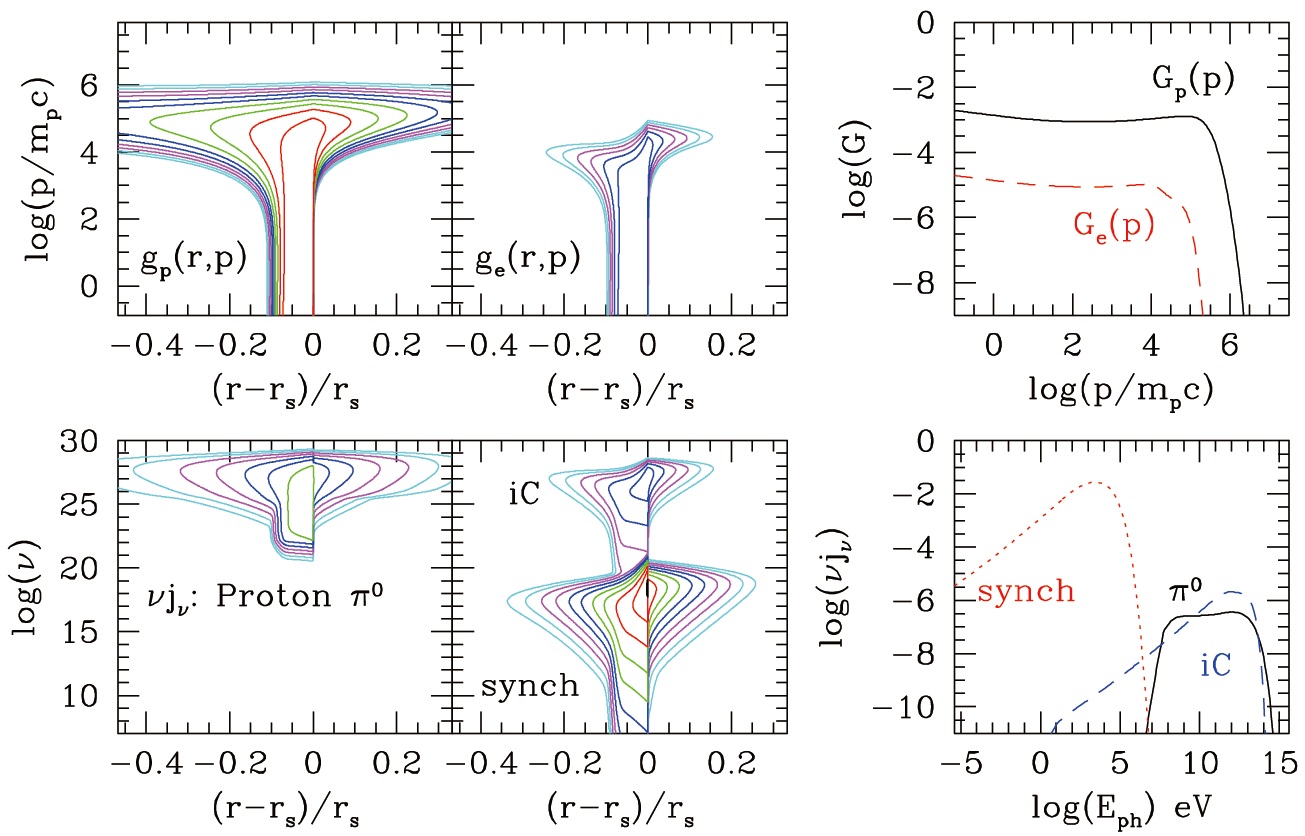
[Fig. 1.] DSA simulation results of a Sedov blast wave from Type Ia supernova (see text for the model parameters). Left four panels: Proton and electron distribution
functions, gp (r,p) = fpㆍp4 and ge (r,p) = feㆍp4, respectively, p-p secondary π0 decay emissivity, νjv(r,ν), and electron synchrotron and iC emissivity, νjv(r,ν) are shown.
Contour intervals are a factor of 10. Right two panels: Volume integrated energy spectra, Gp (p) (solid line) and Ge (p) (dashed), for protons and electrons, respectively,
the volume integrated radiation spectra of π0 decay (solid), synchrotron (dotted), and iC scattered (dashed) emissivities (where Ke/p = 10-2 is adopted). The results are
shown at the age of 255 years.
shocks. If the magnetic fields are amplified to ~30 μG in the upstream region of SNRs, CR ions of charge number Z might gain energies up to Emax ~ 1015.5 Z eV, which may explain the all-particle CR spectrum up to the second knee at ~1017.3 eV with rigidity-dependent cutoffs (Hillas 2005).
Recent γ-ray observations of several SNRs in GeV-TeV bands can be interpreted by a combination of decay of neutral pions produced in nuclear interactions between CR protons and the ambient medium and inverse Compton (iC) scattering of the background radiation by CR electrons (Acciari et al. 2011, Giordano et al. 2012, Morlino & Caprioli 2012). Fig. 1 shows the results of a DSA simulation of Type Ia SNR for the following parameters: the ejecta mass, Mej = 1.4 M⊙, the SN explosion energy, Eo = 1051 ergs, the hydrogen number density, nH,0 = 0.3 cm3, the gas temperature, T0 = 3 × 104 K, and the constant magnetic field strength, B0 = 30 μG for the background flow (Kang et al. 2012). The proton to electron number ratio is assumed to be Ke/p = 10-2 in the right panels. One can see that the spatial and spectral distribution of protons (gp = fp p4) and electrons (ge = fe p4) behave differently because of electronic synchrotron and iC energy losses. The distribution of nonthermal emissions depends on the magnetic field strength and the background density in addition to fp and (fe. Obviously, the importance of π0 decay relative to electron iC emissions should scale with nH,0/Ke/p, once the energy spectra of CR protons and electrons and the background radiation field are given. So multi-band observations of nonthermal emissions from SNRs can be used to explore the complex nonlinear plasma processes in the DSA theory.
In fact, steep γ-ray photon spectra of N (Eυ) ∝ Eυ?Γ with Γ~ 2.2-2.4 GeV band, observed in several young SNRs, may not be consistent with the spectra of CR protons and electrons predicted from nonlinear DSA modeling of SNRs (Abdo 2010, Acciari et al. 2011, Caprioli 2011). Another observational evidence indicating a soft source CR spectrum comes from the measurements of CR nuclei at Earth up to ~1014 eV by TRACER, whose flux spectrum can be fitted by J(E)∝E-2.67 (Ave et al. 2009). If the mean propagation path length of CRs scales with the particle energy as Λ∝ E-0.6, as commonly adopted, the source spectrum, N(E)∝ E-α with α ~ 2.3-2.4, is preferred. However, if order of 10% of the SN explosion energy is to be transferred to CRs, the flow structure could be significantly modified by the CR pressure, resulting in a concave particle spectrum which is harder than the test-particle power-law of E-2 for E ≫1 GeV (Berezhko et al 2009, Edmon et al. 2011). Presumably, these discrepancies call for a substantial revision of the standard nonlinear DSA at strong shocks (Kang 2010, Caprioli 2012). Thus in order to reconcile the DSA predictions with these observations, the DSA efficiency at typical SNRs should not be much higher than 10% and the energy spectrum of shock accelerated particles should be softer than the canonical test-particle power-law. One way to soften the CR spectrum is to include fast Alfvenic drift in the shocks precursor, which reduces the velocity jumps that CRs experience across the shock (Caprioli 2012, Zirakashvili & Ptuskin 2008, 2012). We will explore this issue using our numerical simulations below.
Here we consider the CR acceleration at quasi-parallel shocks where the magnetic field lines are parallel to the shock normal. We solve the following diffusion-convection equation (Skilling 1975):
where g = f (r,p,t)ㆍp4 is the isotropic part of the pitch-angle averaged CR distribution function, y = ln (p/mp c), and κ(r,y) is the spatial diffusion coefficient parallel to the mean magnetic field. The velocity uw represents the effective relative motion of scattering centers (MHD turbulences) with respect to the bulk flow velocity, u. The basic gas dynamic equations and details of the spherical Cosmic-Ray Amr Shock (CRASH) code can be found in Kang & Jones (2006).
The electronic synchrotron/iC cooling constant is defined as b(p) = -dp/dt = (4 e4/9 me4 c6) Be2 P2 in cgs units, where e and me are electron charge and mass, respectively. The effective magnetic energy density, Be2 = B2 + Br2, includes the energy density of the ambient radiation field, Br = 6.5 μG, which combines the cosmic background and mean Galactic radiation fields (Edmon et al. 2011). The cooling term for protons is set to be b (p) = 0.
Thermal Leakage Injection: In order for suprathermal particles to leak upstream across the shock transition layer, whose thickness is order of the gyroradius of downstream thermal protons, the particle speed must be several times larger than the downstream flow speed, u2. So injection of protons and electrons from the postshock thermal pool into the CR population via wave-particle interactions are emulated by a phenomenological model, in which particles above an ‘effective’ injection momentum, pinj ? 6.6 mpu2, are allowed to cross the shock upstream (Kang et al. 2002). This injection model results in the injected particle fraction, ξ =ncr,2/n2, that ranges from 10-5 to 10-3.5 and decreases in time as the shock slows down. Protons and electrons of the same rigidity (R = pc/Ze) are injected in the same manner in the simulations.
Magnetic Field Amplification: CRs streaming upstream in the shock precursor generate both resonant Alfven waves (Bell 1978, Lucek & Bell 2000) and nonresonat waves (Bell 2004), and in turn amplify the turbulent magnetic fields by orders of magnitude. As mentioned in Introduction, several plasma and MHD simulations have shown that both B∥/B0 and B⊥/B0 can increase by a factor of up to ~10-45 via CR streaming instabilities (e.g., Riquelme & Spitkovsky 2009, 2010, Guo et al. 2010, Gargate & Spitkovsky 2012, Rogachevskii et al. 2012). Furthermore, there are several other instabilities that may amplify the turbulent magnetic fields on scales greater than the CR gyroradius (Schure et al. 2012). Here, we adopt the prescription for MFA due to CR streaming instabilities that was suggested by Caprioli (2012), based on the assumption of isotropization of the amplified magnetic fields. In the upstream region (r > Rs),
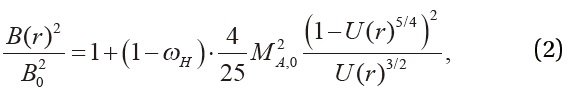
where MA,0 = us(t)/VA,0 is the Alfvenic Mach number for the instantaneous shock speed with respect to the far upstream Alfven speed,
is the flow speed in the shock rest frame normalized by the shock speed. The factor (1-ωH) accounts for loss of the magnetic field energy due to wave dissipation (see below).
Alfvenic Drift: The magnetic field fluctuations generated by CR streaming instabilities drift with respect to the underlying flow in the shock precursor (Skilling 1975). In the upstream region, the mean drift speed of scattering centers is assumed to be the Alfven speed along the parallel magnetic field,
pointing away from the shock. As mentioned above, the amplified magnetic fields are likely to be nearly isotropized by various
instabilities, so the effective Alfven speed could be defined by the local amplified field B(r) given by Eq. (2) In order to consider the uncertainty in the model, we set the local Aflven speed as
where fA is a free parameter that ranges 0.1-1.0 (Zirakashvili & Ptuskin 2008, Lee et al. 2012). In the postshock region, the Alfvenic turbulence is nearly isotropic in planar shocks, so the drift is expected to be uw,2 ? 0 (Jones 1993). For spherical Sedov-Taylor blast waves, however, the CR pressure decreases behind the shock, so Alfven wave may drift inward with uw,2 ? - VA downstream of the shock. We will consider the models with both upstream and downstream drift (SNR4 model).
Wave Dissipation and Precursor Heating: In the late Sedov-Taylor stage, the magnetic turbulence can dissipate due to nonlinear wave-wave interactions and ion-neutral collisions (Ptuskin & Zirakashvili 2005). Gas heating due to the Alfven wave dissipation in the precursor is prescribed by the following term:
where Pc is the CR pressure. The parameter ωH is introduced to control the degree of wave dissipation and a fiducial value of ωH = 0.5 is adopted. For larger values of ωH, of course, the magnetic field amplification is suppressed (see Eq. (4)).
Free Escape Boundary: The magnetic turbulence on scales of the gyroradius of the highest energy CR protons may not provide sufficient scattering to confine those particles around the shock. In order to account for escape of the protons near pp,max, we implement a free escape boundary (FEB) at an upstream location by setting f(rFEB,p)=0 at rFEB=(1+ζ)rs(t) where ζ=0.1-0.5. This FEB condition can mimic escape of the highest energy particles with a diffusion length, κ(p)/us(t)>ζrs(t). Since the shock speed decreases while the shock radius increases in time, with this FEB the mean momentum of escaping particles decreases as <pesc>∝t-1/5.
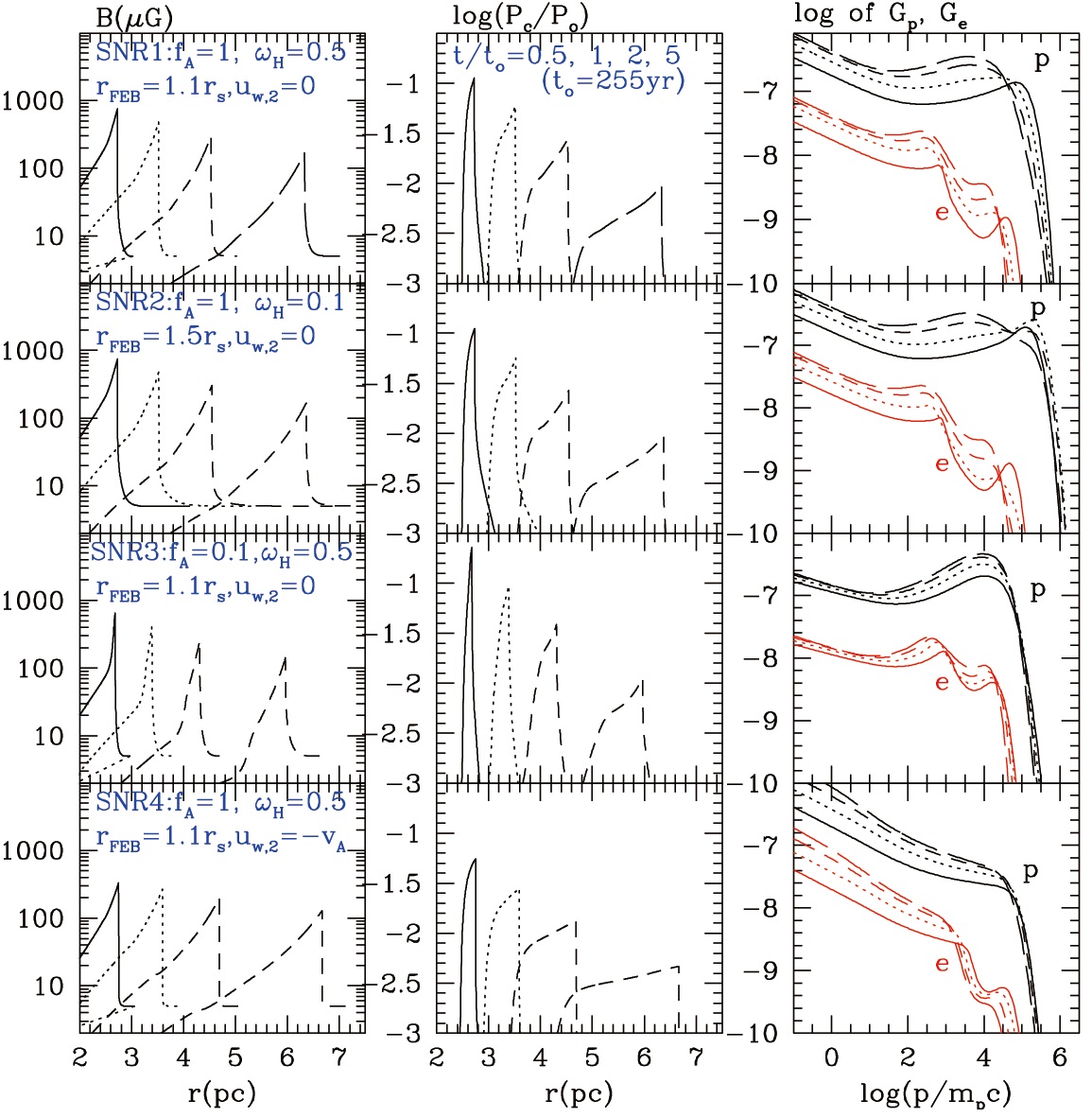
Sedov-Taylor Self-Similar Solution: Here we consider a Type Ia supernova explosion with the ejecta mass, Mej = 1.4 M⊙, and the explosion energy, Eo = 1051 ergs. The background ISM is characterized by nH = 0.3 cm-3 and T0 = 3 × 104 K, and assumed to be completely ionized with the mean molecular μ = 0.61. The background magnetic field strength is set to be B0 = 5 μG, so the Alfven speed is VA,0 = 16.8 km s-1 and the Alfvenic Mach number is MA ? 180 (us/3000 km s-1). The rest of models parameters are summarized in Table 1. We consider SNR1 model as a fiducial case. The effects of FEB are explored by SNR2 model with ζ = 0.5. In SNR3 model, Alfven speed is reduced by setting fA = 0.1. SNR4 model includes the effects of Alfvenic drift in the downstream region, i.e., uw,2=-VA(r). In all four models, the wave drift speed in the upstream region is set to be uw,1 = +VA (r).
For a Type Ia SNR, the highest proton energy (pp,max) is achieved at the beginning of the Sedov-Taylor (ST) stage and the transfer of explosion energy to the CR component occurs mostly during the early ST stage. In order to account for the CR acceleration from free expansion stage through ST stage, we begin the calculations with the ST similarity solution at t/to = 0.2 and follow the evolution of the forward shock during the early ST stage up to t/to =10. We will show below the energy conversion to CRs saturates at ~30% after t/to ? 10.
Fig. 2 shows the spatial profiles of the amplified magnetic field and the CR pressure, and the volumeintegrated distribution functions of protons and electrons, Gp(p) = 4π ∫ gp (r,p)r2dr and Ge(p) = 4π ∫ ge(r,p)r2dr, respectively, for models SNR1-SNR4. One can see that the spatial profile of B (r,t) has a smooth precursor, and the magnetic field strength decreases in time. For example, the postshock magnetic field strength is B2 ? 200-500 μG at the SNR age of t ? 255 yr. These overall pictures seem to be consistent with the observations of young SNRs, which were discussed in Introduction.
Since the MFA factor scales with the degree of flow modification in the precursor (see Eq. (2)) and the diffusion length, ldiff ∝ p, increases with the particle momentum, the low energy part of the CR spectrum is softened by Alfvenic drift much more than the high energy part (Kang 2012). As can be seen in the right panels of Fig. 2, the concave curvature in the energy spectra, Gp and Ge, does not disappear entirely even with Alfvenic drift, except in SNR4 model. The volume integrated electron energy spectrum steepens by one power of the momentum for p > pe,br/mpc ? 103
due to synchrotron/iC cooling. The peak in Ge near pe,max comes from the electron population in the upstream region, which cools much less efficiently due to weaker magnetic fields there.
Comparison of Gp and Ge in the four models demonstrates that the high energy cutoffs in the CR energy spectra depend on time evolution of us(t) and B(r,t) in addition to the model parameters for Alfvenic drift, wave damping, and FEB. In SNR4 model, in which the Alfvenic drift in the postshock region is included as well, the CR spectra are much softer, the postshock CR pressure is smaller by a factor of two or so, compared to SNR1 model.
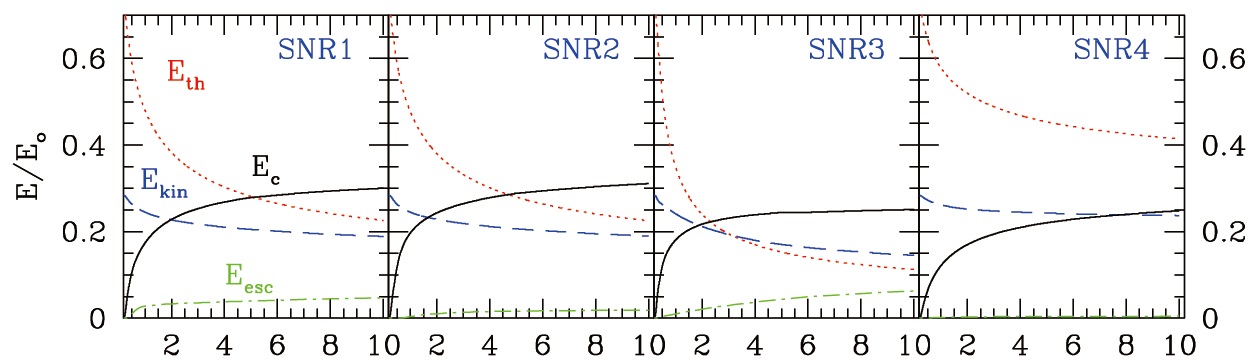
Fig. 3 compares how different energy components change in time: the kinetic energy, Ekin, thermal energy, Eth, and CR energy, Ec, expressed in units of Eo. The fraction of the explosion energy transferred to CRs asymptotes to 0.25-0.3 in these models, which should be sufficient to explain the CR luminosity of the Galaxy. In SNR3 model, the CR proton spectrum, Gp, is harder than that of other three models, and so more high energy particles escape from the shock, resulting in a greater energy loss, Eesc (green dotdashed lines). We note that the CR energy (Ec) achieved
during Sedov-Taylor stage is similar in all four SNR models, although the CR proton and electron spectra depend sensitively on the details of DSA model, and behave rather differently (see Fig. 2).
In this study we have explored how wave-particle interactions and plasma instabilities govern nonlinear DSA and the resulting nonthermal emissions from SNRs. As demonstrated in Figure 1, the CR electron spectrum near the high energy cutoff determines the X-ray synchrotron emissions and the iC scattered emissions in GeV-TeV band. The former depends on the distribution and evolution of the magnetic fields, while the latter depends on the background radiation field. The γ-ray emissions due to π0 decay depend on the CR proton spectrum and the background matter density. Of course, the CR energy spectra are regulated by the degree of MFA and radiative cooling (e.g., pp,max and pe,max), and by particle escape due to lack of plasma waves on relevant scales. Thus we need to understand better waveparticle interactions at nonrelativistic collisionless shocks in order to make quantitative predictions for the CR spectra and nonthermal radiation spectrum due to those CRs.