High-level Petri Nets provide a graphical and mathematical tool for system description and analysis that can be applied effectively to issues of parallel and asynchronous workflow [1]. Vigorous research and development on Petri Nets in recent years has led to a widening of their field of application. Petri Nets have become the preferred modeling tool for net systems that have a variety of abstraction levels [2]. They have been used widely in the areas of discrete event systems analysis, flexible manufacturing systems (FMS), automatic control, computer network performance analysis and protocol verification, parallel program design and analysis, knowledge inference, artificial neural networks, and decision models [3].

One of the main purposes of using Petri Nets to model an actual system is to analyze the properties and functions of the actual system with the assistance of a system model. We research Petri Nets for the purpose of applying them to areas of artificial intelligence, such as knowledge expression and the establishment of formalized reasoning models, expressing relationships among various activities, reasoning logically based on modeling through a known initial state and initial conditions, calculating the credibility of each inference result through fuzzy inference reasoning, and determining reasonable inference results. In order to achieve this purpose, we first study the reachability of a Petri Net.

In research on Petri Nets, reachability is probably the most basic dynamic property and the decidability of the reachability problem is probably the most important open problem in the mathematical theory of Petri Nets and related formalisms. In a sense, research on reachability is the foundation for research on other dynamic properties of Petri Nets, because many other problems can be described using reachability. The reachability problem for Petri Nets is to decide, given a Petri Net N and a marking M, whether M ∈ R(N). Clearly, this is a matter of marking the reachability graph defined above, until we reach the requested marking or we know it can no longer be found. This is more difficult than it might seem at first: the reachability graph is generally infinite, and it is not easy to determine when it is safe to stop. In fact, this problem was shown to be EXPSPACE-hard [4] years before it was shown to be decidable at all. Papers continue to be published on how to decide the reachability efficiently [5].

While reachability seems to be a good tool for finding erroneous states, the constructed graph usually has far too many states to calculate for practical problems. To alleviate this drawback, linear temporal logical (LTI) is customarily used in conjunction with the tableau method to prove that such states cannot be reached. LTL uses the semi-decision technique to find if a state can be reached, by finding a set of necessary conditions for the state to be reached and then proving that those conditions cannot be satisfied.

Thus, if the decision problem of reachability can be solved, then other dynamic properties such as activity are expected to be solved. Unfortunately, it is not easy to find a general algorithm that can determine the reachability of any Petri Net, especially an unbounded Petri Nets. Since the reachability decision problem has at least exponential space complexity and no effective algorithm is found by now, so if we can find and prove some Petri Net subclasses that can use the satisfiability of the state equation to decide the reachability, it is also an important and indispensable work.

It has been proved that, for the live T-system and live weighted T-system, the reachability is equivalent to the satisfiability of the state equation, based on these existing conclusions, this paper proposed a subclass of live weighted Petri Net-Live Single Branch Petri Net, and proved that for this kind of Petri Net, the reachability is equivalent to the satisfiability of the state equation. That is to say, for living single branch Petri Net, we can make use of the satisfiability of state equation to determine its reachability.

The rest of this paper is organized as follows. Section 2 gives a short review and comparison of related studies and then presents the contributions of our paper. Section 3 describes the basic notations and definitions of Petri Nets. Section 4 first shows two examples to illustrate why using state equations cannot decide the reachability of any kind of Petri Net, then proposed a subclass of Petri Net, that can use the satisfiability of state equation to decide the reachability, and then proved the validity. Section 5 introduces parts of existing reachability decision methods. Finally we draw conclusions and suggest future studies.

Our research relates to a number of areas, especially Petri Netbased formalisms, dynamic behavior, and synchronized concurrent systems research. Since for some subclasses of Petri Net, the state equation has non-negative integer solution is not only the necessary condition but also the sufficient condition of M can reach from M₀, so for these kind of Petri Net, the reachability is equivalent to the satisfiability of the state equation. Therefore, it can significant simplify the decision of reachability (get rid of the judgment of the existence of legitimate sequence). So to find and prove which kinds of Petri Nets subclasses can have this property is an item of work with extraordinary significance. Many researchers have devoted themselves to find the Petri Net subclasses with this property. Here we highlight some relevant works in these fields.

Liu and Chen [6] have found a subnet of Petri Net: ∑ = (S, T; F;W;M₀), if it satisfied the condition ∀_s ∈ S → │？s│ ≤ 1, then for this kind of Petri Net subclass, the reachability is equivalent to the satisfiability of the state equation. Murata [7] has found that for the live T-system, the reachability is equivalent to the satisfiability of the state equation. Xu and Wu [8] further found and proved that for the live weighted T-system, the reachability is also equivalent to the satisfiability of the state equation. Bao et al. [9] have defined a minimal-trapcircuit Petri Net and backward-circuit Petri Net, and proved that the reachability problem of this two kinds of Petri Net subclasses is equivalent to the satisfiability of the state equation if no token-free minimal circuit exits under the initial marking.

Despite these previous researches, some other researchers devote themselves to use Petri Net as a tool for context inference, modeling and analyzing of discrete event and so on. Lee et al. [10] propose a context inference model which is based on the socalled fuzzy colored timed Petri Net. The model represents and handles the sequential occurrence of some events along with involving timing constraints, deals with the multiple entities using the colored Petri Net model, and employs the concept of fuzzy tokens to manage the fuzzy concepts [10]. Mo et al. [11] proposed a fuzzy transition timed Petri Net with fuzzy theory to determine the optimal transition time. Kim et al. [12] models traffic system with fuzzy discrete event system’s character in fuzzy transition timed Petri Net, and based on it to design a traffic signal controller.

Based on the abovementioned studies, in this paper, we put forward a subnet of a Petri Net-a live single branch Petri Net whose reachability is equivalent to the satisfiability of the state equation.

Petri Net has many good features that can be used to analyze and describe the system. It can simulate the system from the perspective control and management, accurately describe the dependency and dependency relationship of the event of in the system, describe the system structure and behavior with unified language and describe the synchronized concurrent systems, provide a new way to solve the different kinds of problems, refer to the literature [13].

Petri Net is a model used to describe distributed systems. It can not only describe the structure of the system, but also simulate the operation of the system. The part that describes the system structure is referred to as a network. In form, a net is a directed bipartite graph without isolated nodes.

A triple N = (S, T; F) which satisfies the following conditions is called a net:

1) S ∩ T ≠ ？

2) S ∩ T = ？

3) F ⊆ (S × T) ∪ (T × S))

4) dom(F) ∪ cod(F) = S ∪ T

Where:

dom(F) = {x ∈ S ∪ T│∃y ∈ S ∪ T : (x, y) ∈ F}

cod(F) = {x ∈ S ∪ T│∃y ∈ S ∪ T : (y, x) ∈ F}

S and T are two disjoint sets (In general they are assumed to be the finite set), that are the basic elements sets of net N. S is called place set and T is called transition set. The elements of S are known as the S-place, which can also be called location and the elements of T are known as the T-transition. F is the flow relation of net N [14].

Suppose N=(S, T; F) is a net, then for all the x ∈ S ∪ T, record

？x = {y│y ∈ S ∪ T ∧ (y, x) ∈ F}

x？ = {y│y ∈ S ∪ T ∧ (x, y) ∈ F}

Here we name ^？x as the pre-set or input set of x, x^？ as the post-set or output set of x, name ^？x ∪ x^？as the extension of element [14].

An extension of a place is the subset of transition set T, and an extension of a transition is the subset of place set S.

Suppose N = (S, T; F;M) is a Petri Net, if there exists a t ∈ T, which satisfies M[t > M’, then M’ is directly reachable form M. If there exists transition sequence t₁, t₂, ..., t_k and identity sequence M₁, M₂,..., M_k, which satisfies: M[t₁ > M₁[t₂ > M₂[t₃ ... > M_k？1[t_k > M_k, Then we say that M_k is reachable form M. All the identifications that are reachable from M are named as R(M), and M ∈ R(M). If the transition set t₁, t₂, . . . , t_k is labeled as σ, then the M[t₁>M₁[t₂>M₂[t₃. . .> M_k？1[t_k> M_k can be labeled as M[σ>M_k [14].

When we use a Petri Net to simulate an actual system, the net ∑ = (S, T; F) describes the structure of the system. Initial marking M₀ is marked of the initial states of the system, and R (M₀) is the totally probable state set of the system that occurs in the operation process.

Based on this, we can define the net system ∑ as follows: here M₀ is the initial marking of ∑, and the reachability marking set of ∑ is the Minimum Set that satisfies the following two conditions:

1) M₀ ∈ R(M₀)

2) If M ∈ R(M₀), and there exists t ∈ T that satisfies M[t>M, then M ∈ R(M₀) ][14].

For the bounded Petri Net, since its reachability marking set R (M₀) is a finite set, we can take R (M₀) as a vertex set, using the directed reachable relations between the markings as arc set to make up a directed graph. This kind of directed graph is called a reachable marking graph of the Petri Net.

Suppose ∑ = (S, T; F;W;M₀) is a Petri Net, M₀ is the initial identifier, t ∈ T. If for ∀M ∈ R(M₀) always exist M’ ∈ R(M), make M’[t >, then the transition t is live. If ∀t ∈ T, t always lives, then the ∑ is a live Petri Net [14].

For a general Petri Net, ∑ = (S, T; F;W;M₀), since exiting an n (n=│T│) dimensional non-negative integer vector satisfied the state equation M = M₀ + A^TX is just a necessary condition but not the sufficient condition of M is reachable from M₀, so we cannot using state equation to decide the reachable marking of ∑.

In the following, we’ll use two examples to show why we cannot use the state equation to decide the reachability for any kinds of Petri Nets.

First, considering the matrix method for analyzing Petri Nets, a matrix A cannot reflect the structure of a Petri Net accurately, because if the transition section uses one position to input and output simultaneously, there will be a self-loop, i.e., the same position of A⁺ and A^？ will occur at the same number, which will be mutually offset by A^？ - A⁺.

Second, there will be missing sequence information in the triggered vector.

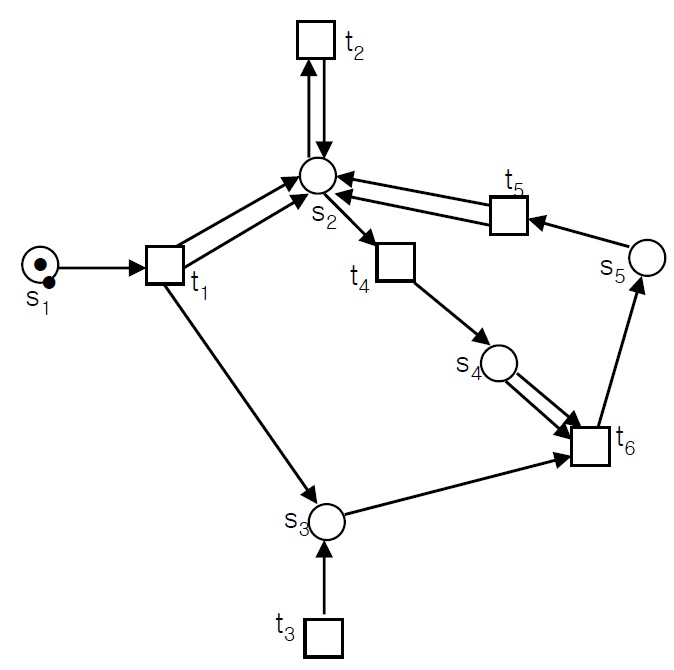
For example, suppose we want to confirm whether the identification (0, 0, 0, 0, 1) can be reached from (1, 0, 0, 0, 0) in Figure 1. If we use the state equation to decide reachability, we get Equation (1):

(For the matrix, the column indicate the place p₁, p₂, p₃, p₄, p₅, the row indicate the transition t₁, t₂, t₃, t₄, t₅, t₆)

Obviously, the solution of this equation is not unique. From this general form, we can know only the relationships among the numbers of the initiation of the transition node, but cannot confirm the sequence of the initiation.

Third, the solution calculated using the state equation might be a false solution.

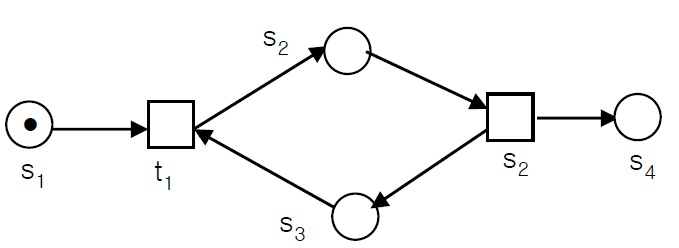
For example, suppose we want to confirm whether the identification (0, 0, 0, 1) can be reached from (1, 0, 0, 0) in Figure 2. If we use state equation to decide reachability, we can get Equation (2):

This equation has a solution of (1, 1). The equation corresponds to the two initiating sequences t₁t₂ or t₂t₁, but neither can be reached, because t₁ and t₂ cannot be enabled in (1, 0, 0, 0). Therefore, we can see from this example that the solution calculated using the state equation might be a false solution.

However, there exits some special Petri Net, the reachability problem is easily to be decided, so it has great significant to find such Petri Net subclass. In the following, we will define

a Petri Net subclass and prove that, for this kind of Petri Net subclass, the reachability is also equivalent to the satisfiability of the state equation.

For a Petri Net∑ = (S, T; F;W;M₀), if identifier M is reachable from M₀ (mark as: M ∈ R(M₀), then there must exist an n-dimensional non-negative integer vector X, satisfying

here A is the incidence matrix of ∑, which is an n×m integer matrix ( │T│=n, │s│=m ). Equation (3) is the state equation of Petri Net ∑. But for a general Petri Net, Equation (3) is just the necessary condition of M ∈ R(M₀), not the sufficient condition, i.e., for any Petri Net, we cannot determine the initiating sequence caused by the transition node by judging whether the Petri Net satisfies the state equation.

However, for some subclass of Petri Net, Equation (3) is the sufficient and necessary condition of M ∈ R(M₀). In the following, we’ll first give the definition of live single branch Petri Net, and then prove for this kind of Petri Net, the reachability is equivalent to the satisfiability of the state equation.

Suppose ∑ = (S, T; F;W;M₀) is a live Petri Net, if ∀_s ∈ S, it must have │^？s│ > 1 ⇒ (s, s) ？ F⁺. Then the Petri Net is called a live single branch Petri Net. Here TX F⁺ is the transitive closure of flow relation F. It means that the Live Single Branch Petri Net cannot have multi pre-set, but can have multi post-set. An example of live single branch Petri Net is shown as Figure 3, here │s₇│=2.

Obviously the live single branch Petri Net includes the live weighted T-system Petri Net which has only one input and one output (∀_s ∈ S : │^？s│ = │s^？│ = 1), but the live single branch Petri Net which we proposed in our paper has one input but multi outputs, it is more general than the live weighted T-system.

Xu and Wu [8] have proved that for the live weighted T-system Petri Net, the reachability is equivalent to the satisfiability of the state equation. In the following, we’ll prove that for the wider one, we can also depend on the state equation satisfiability to decide the reachability.

Since it is depicted in extensive literature that the equation M = M₀ + A^TX is the necessary condition of the reachability of a Petri Net, we will prove here only that for a live single-branch Petri Net, equation M = M₀ + A^TX is also the sufficient condition for reachability.

Before we prove this, we first prove two propositions.

Proposition 1:

Suppose ∑ = (S, T; F;W;M₀) is a live weighted Petri Net. If for any M ∈ R(M₀) for which the n-dimensional non-negative integer vector X satisfies M+A^TX ≥ 0, we can find a t ∈ TX that satisfies M[t>, then the sufficient and necessary condition of identifier M_d being reachable from M₀ is that there exists an n-dimensional non-negative integer vector X satisfying the state equation M_d = M₀ + A^TX. Here TX={t_i│t_i ∈T and X(i)>0} (X(i) is the ith component of vector X) .

Proof:

(1) The necessity of this theorem follows obviously from the basic properties of Petri Nets.

(2) Now we prove the sufficiency

Suppose

Since M_d = M₀ + A^TX ≥ 0, there exists t_il ∈TX, 1 ≤ i₁ ≤ n, satisfying M₀[ti_l>M_l. In addition, because M₁ = M₀ + A^TE_i1 (here Eil is an ndimensional non-negative vector whose i1th component is 1, and whose other components are 0), suppose X_l=X-E_i1, then M₁ + A^TX₁ = M₁ + A^TX (X ？ E_i1) = M₀ + A^TX ≥ 0. Also, because M_l ∈ R(M₀), there exists ti₂ ∈ TX_l, that satisfies M₁[ti₂>M₂. Suppose X₂=X₁- E_i2, then M₂ + A^TX₂ ≥ 0 and M₂ ∈ R(M₀), so there exists ti₃ ∈ TX₂, satisfying M₂[ti₃>M₃. Continuing the recursion, we can get

M3[ti4 > M4; ... ;MK？1[tiK > MK = Md.

Finally we can conclude that identifier M_d is reachable from M₀.

This proves the sufficiency, and thus also proposition 1.

Proposition 2:

Suppose ∑=(S, T; F;W;M₀) is a live single-branch Petri Net, then for any n dimension non-negative integer vector X that satisfies M₀ + A^TX ≥ 0, there exists t ∈ TX, satisfying M[t> (Here TX={t_i│t_i ∈T and X(i)>0}).

Proof: We use reductio ad absurdum.

Suppose an n dimensional non-negative integer vector satisfies M₀ + A^TX ≥ 0, then for all t ∈ TX, there is no M₀[t>. By constructing the sequence of ti_l, si₁, ti₂, si₂,..., ti_r with the following algorithm, we will find a contradiction in the sequence.

Algorithm:

Step 0: ① Randomly select a t∈TX, labeled as til;

② S1 = {s│s ∈ ？ti1, and M0(s) < W(s, ti1) //W is the weighted function of ∑, because the //M0[til> is false, so S1≠0.

③ Counting variable j:=1;

Step l: ①Tj+1 = {t│t ∈ ？Sj, and t ∈ TX

② If Tj+1 ≠= ？ then

{

Randomly select a t∈Tj+1, labeled as tij+1, and label sij as the place S of ？tij∩ t？ij+1 (here, if there are many places in ？tij ∩ t？ij+1, then select one of them randomly);

}

Else // Tj+1=？

Jump to Step 2.

③ If tij+1 = tk and 1 ≤ k ≥ j then Jump to Step 2. Else j:=j+l, Jump to Step l.

Step 2: End.

It is easy to see that since the elements in T are finite, the algorithm can be terminated. We can finally get the sequence: ti_l, si₁, ti₂, si₂, . . . , ti_r, where ti_j ∈TX, j= l, 2,. . . , r.

We discuss the sequence ti_l, si₁, ti₂, si₂, . . . , ti_r according to the termination conditions of the above algorithm with the following two cases:

(1) Case 1:

When ti_j=ti_k(1≤k<r), the sequence will be a return circuit

Analyze the loop ti_k,si_k,. . . ,ti_r？1,ti_k. Since │^？S│ > 1 ⇒ (s, s) ？ F⁺, so│^？Si_j │ = 1(j = k, k + 1, ... r ？ 1). Also because some places si_j in the sequence do not have enough tags to initiate the transition ti_j (j=k,k+1,. . . ,r-1) of the sequence, and for any Si_j (j=k,k+ 1,. . . ,r-1) in the sequence, ^？Si_j = {ti_j + 1}, therefore tags outside of the sequence cannot flow to places within the sequence, i.e., any transitions ti_j (j=k,k+1,. . . ,r-1) within the sequence will not be initiated, which is contradictory to the fact that ∑ is a live Petri Net.

(2) Case 2:

When T_j+1 ≠ ？, the sequence will be:

(where ti_j ≠t_ik,l≤k<r)

Since M₀[ti_l> is false, there exists a place sir, that satisfies M₀(si_r)<W(si_r,ti_r), and there is no transition t in the ^？si_r that satisfies t∈TX. Now let M₁ = M₀ + A^TX, since ti_r ∈TX, i.e., X (i_r)>0, but the number of the tags of si_r is smaller than the weight of the side W(si_r,ti_r), so there must exist a M₁(si_r)<0, which is contradictory with M₁ = M₀ + A^TX ≥ 0

Thus proposition 2 is proved.

Proposition 3:

Based on the above conclusions (conclusions 1 and 2) we will prove, for any live single-branch Petri Net ∑ = (S, T; F;W;M₀), the sufficient and necessary condition of identifier M_d being reachable from M₀is that there exists an n-dimensional nonnegative integer vector X, that satisfies the state equation M_d = M₀ + A^TX.

Proof:

The necessity of this theorem follows obviously from the basic properties of Petri Nets.

Now let us prove the sufficiency:

Since the ∑ = (S, T; F;W;M₀) is a live single-branch Petri Net, according to conclusion 2, we know that for any n-dimensional non-negative integer vector X that satisfies M₀ + A^TX. ≥ 0, there must exist a t∈TX, making the M₀[t>. Here TX = {ti│ti∈T and X(i)>0}

Then according to proposition 1, since the ∑ = (S, T; F;W;M₀) is a live single-branch Petri Net, for any n-dimensional non-negative integer vector X that satisfies M∈R(M₀), and M + A^TX ≥ 0, there must exist t∈TX, that makes the M[t>. Hence, the sufficient and necessary condition of identifier M_d being reachable from M₀ is that there exists an n-dimensional nonnegative integer vector X that satisfies the state equation M_d = M₀ + A^TX, where TX = {ti1ti∈ T and X(i)>0}(X(i) is the i^th component of vector X)

As a result, we can draw the conclusion that: Suppose ∑ = (S, T; F;W;M₀) is a live Petri Net, if ∀_s ∈ S, it must have │^？s│ > 1 ⇒ (s, s) ？ F⁺, then for this kind of Petri Net, if exits and only exits an n dimensional non-negative integer vector X, satisfies the state equationM_d = M₀+A^TX, then the identifier M_d being reachable from M₀. Till now, we have found a way to decide the reachability of Live Single Branch Petri Net.

Petri Nets are a tool for system description and analysis. Reachability is one of the most basic properties in Petri Net research. We research Petri Nets for the purpose of applying them to areas of artificial intelligence, such as knowledge expression and the establishment of formalized reasoning models, expressing relationships among various activities, reasoning logically based on modeling through a known initial state and initial conditions, calculating the credibility of each inference result through fuzzy inference reasoning, and determining reasonable inference results. In order to achieve this purpose, the first task is to research the reachability of Petri Nets. In a sense, reachability is the foundation of the study of other dynamic properties of Petri Nets. Many problems on Petri Nets can be described by it, so the reachability decision problem is therefore one of the most important topics in Petri Net theory.

Methods that can be used to analyze the reachability of a Petri Net include the reachable marking graph and coverability tree, the correlation matrix and state equation, and Petri Net language. Each method has its advantages and disadvantages. Sometimes we can combine them, so as to analyze the dynamic properties of a Petri Net.

Although, using state equation cannot decide the reachability for all kinds of Petri Net, bur since this method is very easy to be grasped and is convenient to be used without the judgment of the existence of legitimate sequence, so if we can prove that for some kinds of Petri Net subclasses, the state equation satisfiability is not only a necessary condition but also a sufficient condition, then it is also an important and indispensable work.

The previous researches have proved that some subclass of Petri Net, such as transition-single-input-circuit Petri Nets, minimum-transition-single-input-trap-circuit Petri Nets, minimumsiphon- circuit Petri Nets, and live weighted T-system Petri Net, the reachability is equivalent to the satisfiability of the state equation.

Based on these previous researches, we found a subclass that includes the live weighted T-system can also use the state equation satisfiability to decide the reachability. In this paper, we defined the Petri Net subclass, and proved that for this kind of Petri Net, if and only if exits an n dimensional non-negative integer vector X, satisfies the state equationM_d = M₀+A^TX, then the identifier M_d is reachable from M₀.

However, our proposed method is suitable only for determining the reachability of a subclass of a Petri Net, so in the future, the key issue in our further study will be to determine how to combine our proposed method in this paper with an improved coverability tree proposed in reference [15] to decide reachability for a general Petri Net.

No potential conflict of interest relevant to this article was reported.