In a number of data-driven modeling tasks, a generative probabilistic model such as a Bayesian network (BN) is an attractive choice, advantageous in various aspects including the ability to easily incorporate domain knowledge, factorize complex problems into self-contained models, handle missing data and latent factors, and offer interpretability to results, to name a few [1,2]. While such models are implicitly employed for joint density estimation, for the last few decades they have gained significant attention as classifiers. A model of this class, the Bayesian network classifier (BNC) [3], has been used in a wide range of applications subsuming speech recognition and motion time-series classification [4-9] and has been shown to yield performance comparable to dedicated discriminative classifiers such as support vector machines (SVMs).

A BNC model represents a density P(c, x) over the class variable c and observation x. Learning its parameters with fully labeled data is traditionally posed as a joint likelihood maximization (ML). However, as the ML learning aims to fit the density for all points in the training data, it may not be directly compatible with the ultimate goal of class prediction. Instead, discriminative learning, typically the conditional likelihood maximization (CML), optimizes the conditional distribution of class given observation, i.e., P(c|x), achieving better classification performance than ML learning in a variety of situations [10-12]. Unfortunately, CML optimization is, in general, complex with non-unique solutions. Typical CML learning methods are based on gradient search that can be computationally intensive.

A mixture model, as a rich density estimator, can potentially yield more accurate class prediction than a single BNC model. Mixture models have received significant attention in related fields and achieved success in diverse application areas [13-15]. In our earlier work [16] we proposed a quite efficient approach to the discriminative density estimation of mixture models. Here we briefly describe the algorithm introduced in [16]. The main goal is to exploit the properties of a mixture to alleviate the complexity of a learning task. This can be done in a greedy fashion, where a mixture component is added recursively to the current mixture with the objective of maximizing conditional likelihoods. Formulated within the functional gradient boosting framework [17], the procedure yields the weight distribution on the data with which a new mixture component can be learned. The derived weighting scheme effectively emphasizes the data points at the decision boundary, a desirable property similarly observed in SVMs.

The method is particularly efficient and easy to implement in that searching for a new mixture component can be done by ML learning with weighted data, and hence is suited to domains with complex component models such as hidden Markov models (HMMs) in time-series classifications that are usually computationally intensive for parametric gradient search. Compared to the conventional expectation-maximization (EM) algorithms, the recursive estimation approach has the crucial advantages of ease of model selection (i.e., estimating mixture orders) and robustness to initial model parameter choice.

Although our earlier approach was limited to fully supervised settings, in this paper we extend it to semi-supervised learning setups where we can make use of a large portion of unlabeled data points in conjunction with a few labeled data. We incorporate the minimum entropy principle in [18] into our recursive mixture estimation framework, where the unlabeled data points are exploited in such a way that the model’s uncertainty in class prediction is maximally reduced. This leads to an objective function comprising the conditional log-likelihoods on labeled data and the negative entropy terms for unlabeled data. Within the functional gradient boosting framework, we derive the stage-wise data weight distribution for this semi-supervised objective.

The paper is organized as follows. In the next two sections, we formally set up the problem and review our earlier approach to the discriminative learning of mixtures in a fully supervised setup. Our proposed semi-supervised discriminative mixture learning algorithm is described in Section 4. In the experimental evaluation in Section 5, we demonstrate the benefits of the proposed algorithms in an extensive set of time-series classification problems on many real-world datasets in semi-supervised scenarios.

Consider a classification problem where a class label is denoted by c ∈ {1, ..., K} for the observation/feature x ∈ X. The input feature x is either vector-valued or structured like sequences of time-series. Let f(c, x) denote a BNC¹ with a class variable c and the input attribute variables x. A BNC can be usually factorized into a (multinomial) class prior f(c) and the class conditional densities f(x|c) = f_c(x). For example, f_c(x) could be a class(c)-specific Gaussian when x is a realvalued vector. Often, f_c(x) may also contain latent variables (e.g., in the sequence classification where x is a sequence of measurements, f_c(x) can be modeled as an HMM with hidden state variables).

As a classifier, the class prediction of a new observation x can be accomplished by the decision rule: c^* = arg max_c f(c|x) = arg max_c f(c, x). Given the (fully supervised) training data

we learn a joint density f(c, x) that minimizes the prediction error. The traditional ML learning optimizes the data joint likelihood

However, the ML learning does not necessarily yield optimal prediction performance unless we are given not only the correct model structure but also a large number of training samples.

The discriminative learning of BNCs effectively represents the class boundaries, and exhibits superior classification performance to ML learning that merely focuses on fitting the density to all points in the training data. CML learning, one of the most popular discriminative estimators, maximizes the conditional likelihood of c given x, an objective directly related to the goal of accurate class prediction. The conditional log-likelihood objective for the training data D is defined as

CML optimization in general does not admit closed-form solutions for most generative models. One typically maximizes it using gradient search. Although it has been shown that CML outperforms ML when the model structure is suboptimal [6,10,11,19], the computational overhead demanded by gradientbased approaches is high, especially for complex models such as HMMs and general BN structures.

1We use the notation f(c, x) interchangeably to represent either a BNC or a likelihood at data point (c, x).

Motivated by the fact that a single BNC can be insufficient for modeling complex decision boundaries (e.g., Gaussian class-conditionals merely represent ellipsoidal clusters), one can enlarge representational capacity by forming a mixture. Let F(c, x) denote a mixture of BNCs, that is,

Note¹ that each component of the mixture is a BNC f_m(c, x). Instead of the usual EM learning for mixture models, a greedy recursive approach was proposed in [16]. At each stage, we add a new BNC component f(c, x) to the current mixture so that it optimizes a certain criterion.

Within the functional gradient optimization framework [17], one considers how to maximize a given objective functional J(F) with respect to the (mixture) function F(z) where z ∈ Z. In the classification setting, z = (c, x), and Z is the classmeasurement joint input domain for the BNC likelihood function f(c, x). The greedy optimization proceeds as follows: for the current mixture estimate F, we seek a new component f such that when F is locally varied as (1 ？ ？)F + ？f for some small positive ？, J((1 ？ ？)F + ？f) is maximally increased. The update equation is:

Maximizing J(F) can be done by gradient ascent (in function space) described by the update rule:

where δ is the step size and ▽_FJ(F) = ∂J(F)/∂F(z) is the functional gradient of J(F) that is also a function obtained by a point-wise partial derivative.

Contrasting (2) with the greedy mixture update rule of (1), the optimal f would be the one that attains the maximal alignment between (f ？ F) and ▽J(F), namely

In the case of a finite number of samples

we estimate (3) as

where w(c, x) = ▽_{F(c, x)}J(F) = ∂J(F)/∂F(c, x). Thus, ▽_{F(c, x)}J(F) serves as a weight for data point (c, x) with which the new f will be learned. Optimization in (4) can be accomplished using a generic gradient ascent-based approach, however, a more efficient recursive EM-like lower-bound maximization was suggested in [16].

Once the optimal component f^* is selected, its optimal contribution to the mixture α^* is obtained as

This optimization can easily be done with any line search algorithm.

It is important to discuss the choice of the objective functional J(F) . For discriminative mixture learning, the conditional loglikelihood is employed in [16] by:

In this case, the functional gradient becomes:

yielding the discriminative data weight:

The discriminative weight indicates that the new component f is learned from the weighted data where the weights are directly proportional to 1 ？ F(c|x) and inversely proportional to F(c, x). Hence the data points unexplained by the model, i.e., F(c, x) → 0, and incorrectly classified by the current mixture, i.e., (1 ？ F(c|x)) → 1, are focused on in the next stage. This is an intuitively desirable strategy for improving the classification performance.

The time complexity of discriminative mixture learning is of the order O(M · (N_ML + N_LS)) where N_ML stands for the complexity of the ML learning and N_LS is the complexity of the line search. Hence, the discriminative mixture learning algorithm complexity is a constant factor of simple generative learning of the base model on weighted data.

1It is also worth noting that, if viewed from the generative perspective, this corresponds to modeling each class with the same number (M) of mixture components (i.e., F(x|c) for all c that have the same mixture order).

So far, we have considered the case where the data is fully labeled. In the semi-supervised setting, we are given the labeled set

and the unlabeled data

Among several known semi-supervised classification approaches, an effective way to exploit the unlabeled data is the entropy minimization method proposed by [18]. The main idea is that we minimize the classification error for the labeled data (e.g., maximizing the conditional likelihood), while forcing the model to have minimal uncertainty in predicting class labels for the unlabeled data. This minimum entropy principle is motivated by minimization of the Kullback-Leibler divergence between the model-induced distribution and the empirical distribution on the unlabeled data that has been shown to effectively partition the unlabeled data into clusters.

Having the negative entropy term for the unlabeled data, the semi-supervised discriminative (SSD) objective can be defined as

where γ ≥ 0 is a controllable parameter that balances the loss term against the negative entropy term. The functional gradient for the new objective is now

Notice that for the labeled data we have a functional gradient identical to that of supervised discriminative mixture learning. For the unlabeled data, however, the gradient terms require further consideration. The main difficulty is that for the unlabeled data x^j (∈ U), we have no assigned class labels. We next consider two different approaches for treating this latent label.

A possible treatment is to assume that we are given all K class labels attached to the unlabeled data x^j. That is, for each data point x^j, we pretend that all possible K pairs

are observed in the training data. Then it follows that:

where H(·) is the entropy function.

Hence, the unlabeled data point x^j induces K data weights:

The unlabeled data weight can be interpreted as follows: (i) The denominator F(x^j) implies the need to focus on the samples that are less highlighted by the current model (regardless of their class labels) in the next stage. (ii) The first term in the numerator log F(c^j|x^j) encourages the model to keep attending to its current decision (c^j) on x^j. (iii) The entropy term in the numerator assigns more weights to the unlabeled samples x^j that have a higher prediction uncertainty in the current model. So, by (ii) and (iii), one can achieve entropy minimization for the unlabeled data.

Despite this intuitive interpretation, one practical issue with this weighting scheme is that the weights can be potentially negative, in which case the optimization in (4) may not be tackled by the lower bound maximization technique. In this case, one can directly optimize it using a parametric gradient search. Alternatively, the pseudo label-based technique presented next can circumvent the negative weight issue.

For the current model, we define the pseudo label for x^j as:

Instead of dealing with all K possible labels for x^j, we consider only a single pseudo-labeled pair

That is, the unlabeled x^j is assumed to be accompanied by

having the following weight:

The intuition discussed in Section 4.1 follows immediately, however, we can now guarantee that the weights for the pseudolabeled data points (11) are always non-negative.

Although dealing with only the best predicted label is convenient for optimization and is a rational strategy to pursue, it is important to note that unlike the all-label approach in Section 4.1 the pseudo-label approach is suboptimal in the objective perspective, essentially amounting to ignoring the negative-weight (pushing-away) effects enforced by the nonbest labels.

We evaluated the performance of the proposed recursive mixture learning in semi-supervised learning settings. We focused on the structured data classification task of classifying sequences or time-series. This is, in general, more difficult than the static multivariate data classification. We used Gaussian-emission HMMs (GHMMs)¹ to model the class conditional densities f_c(x) for the real multivariate sequence x. In our recursive mixture learning, we need to learn GHMMs with weighted data samples, and this can be done by a fairly straightforward extension of the regular EM-based GHMM learning. The detailed EM steps can be found in [20]. The competing approaches whose performance will be contrasted are summarized in Section 5.1, while in Section 5.2 we describe the datasets and report the results.

A simple and straightforward approach to dealing with partially labeled data is to ignore the unlabeled data points. In this section, we first summarize the fully supervised classification algorithms with which we compare our approach. These algorithms are then extended to handle unlabeled data by the wellknown and generic adaptive semi-supervised method called self-training.

The first approaches we describe are model-based, where we use (single) BNC models trained by ML and CML. In CML, the gradient search starts with the ML estimate as the initial iterate. Related to the proposed recursive discriminative mixture learning, we compare the proposed method with [21]’s boosted Bayesian network (BBN), an ensemble-based discriminative learning method for BNCs that treat f(c, x) as a (weak) hypothesis, namely c = h(x) = arg max_c f(c|x), within a boosting [22] framework. For each stage, AdaBoost’s weights w on data (c, x) are used to learn the next hypothesis (BNC) via weighted ML learning:

This approach has been shown to inherit certain benefits from AdaBoost such as good generalization by maximizing the margin. However, the resulting ensemble cannot be simply interpreted as a generative model since the learned BNCs are just weak classifiers to be combined for the classification task.

In addition to the model-based approaches, we also consider two alternative similarity-based approaches that have exhibited good performance in the past, especially on sequence classification problems: dynamic time warping (DTW) and the Fisher kernel [23]. DTW is a dynamic programming algorithm that searches for the globally best warping path. Often, imposing certain constraints on the feasible warping paths has been empirically shown to improve the classification performance [24-26]. For instance, the Sakoe-Chiba band constraint [24] restricts the maximum deviation of matching slices from the diagonal by p% of the sequence length. Thus p = 0 and p = ∞ correspond to the naive Euclidean distance (defined only if the lengths of two sequences are equal) and the standard (unconstrained) DTW, respectively. Recently, [26] proposed an adaptive band approach that estimates the function spaces of time warping paths. In this setting, class-specific warping-path constraints are learned for each class that reflect the warping variations of the samples within it.

The Fisher kernel between two sequences x and x′ is defined as the radial basis function (RBF) evaluated on the distance between their Fisher scores with respect to the underlying generative model. More specifically, in binary classification, k(x, x′) = e^{？？U_x？U_x′？2/(2σ2)}, where U_x = ▽_θlog P_c=+(x). Here P_c=+(x) indicates the likelihood of the HMM usually learned by ML from the examples of the positive class only. The RBF scale σ² is determined as the median distance between the Fisher scores corresponding to the training sequences in the positive class and the closest Fisher score from the negative class in the training data [23]. The multi-class extension is made using a set of one-vs-rest binary problems.

As a baseline, we also consider a static classifier (e.g., SVM) that treats fixed-length (window) segments from a sequence as iid multivariate samples. Specifically, for a window of size r, the class-sequence data pair (c, x) is converted to rd-dim iid samples,

At the test stage, the class label is determined by majority voting over the predicted segment labels.

The competing methods are summarized below:

ML: ML learning of f(c, x).

CML: CML learning of f(c, x).

RDM: Recursive discriminative mixture learning [16].

BBN: Boosted Bayesian networks [21].

NN-DTW (B%): The Nearest Neighbor classifier based on the DTW distance measure where B is the best Sakoe- Chiba band constraint selected by cross validation over the candidate set: {∞%, 30%, 10%, 3%}.

FS-DTW: The function-space DTW learning [26].

SVM-FSK: The SVM classifier based on the Fisher kernel. The SVM hyperparameters are selected by cross validation. To handle multi-class settings, we perform binarization in the one-vs-rest manner. We then employ the winner-takes-all (WTA) strategy which predicts the multi-class labels by majority voting from the outputs of the one-vs-others binarized problems1.

SVM-Win (R%): An SVM classifier that treats fixedlength window segments as iid multivariate samples where R is the relative window size with respect to the sequence length (R = 100r/T). We use the RBF kernel in rd dimensional vector space. We report the best (relative) window size R selected by cross validation over a candidate set: {0% (window size r = 1), 10%, 20%, 30%, 50%}.

SSRDM: Semi-supervised recursive discriminative mixture learning (proposed approach).

In the experiments, we split the data three-fold: labeled training data, unlabeled training data, and test data. All the other approaches listed above are fully supervised, making use of only the labeled data for training. On the other hand, our semisupervised discriminative mixture learning algorithm (denoted by SSRDM) exploits the unlabeled training data in conjunction with the labeled data. Throughout the evaluation we make use of the all-label strategy in (11) as it consistently demonstrated performance superior to the pseudo-label alternative.

We not only demonstrate the improvement in prediction performance achieved by SSRDM compared to supervised methods that ignore the unlabeled data, but we also contrast it with the generic self-training algorithm, a generic method of extending fully supervised classifiers to semi-supervised setups, often very successful and the most popular method in use. We apply the self-training algorithm to each of the supervised methods listed above. The self-training algorithm is described in pseudocode in Algorithm 5.1.

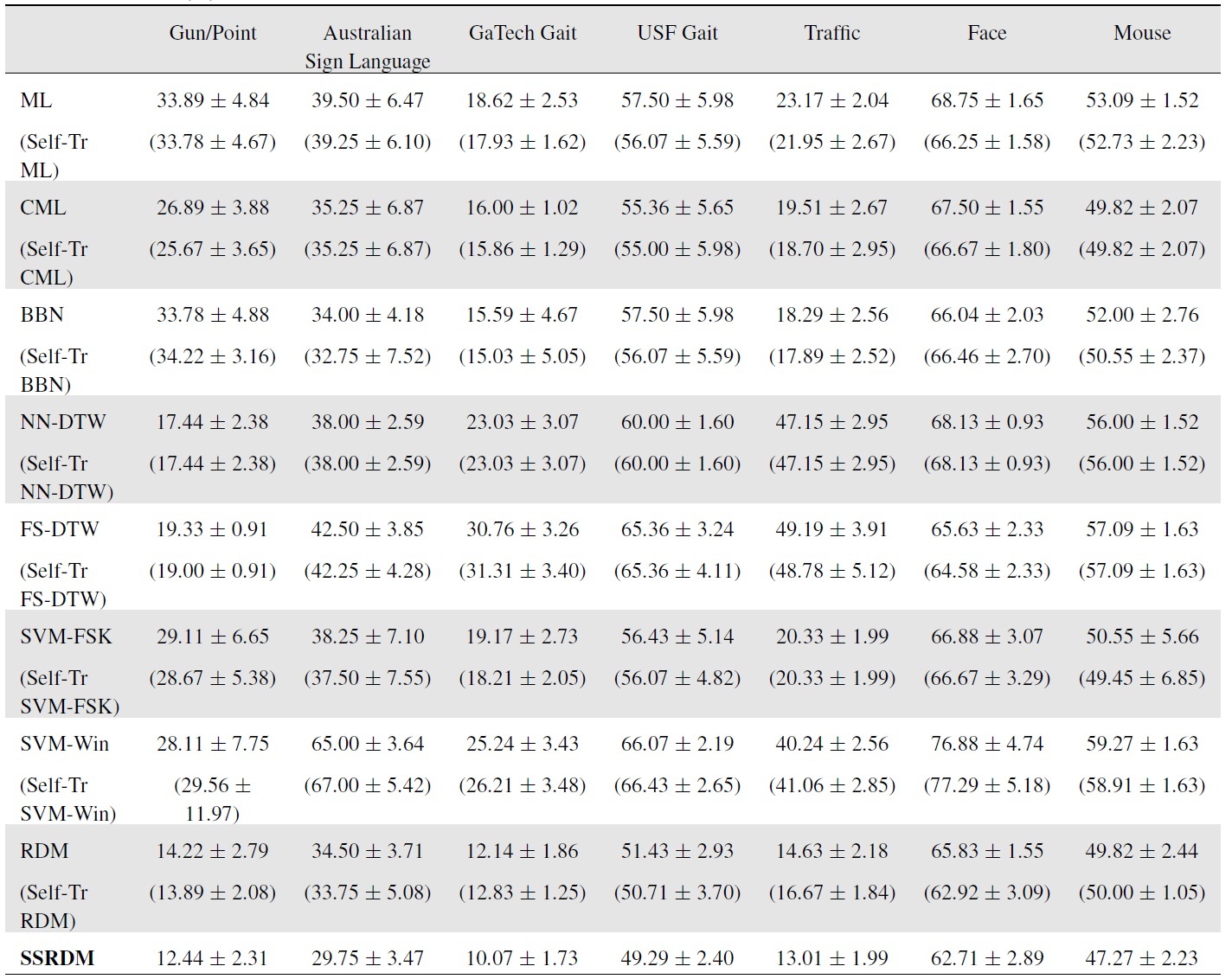
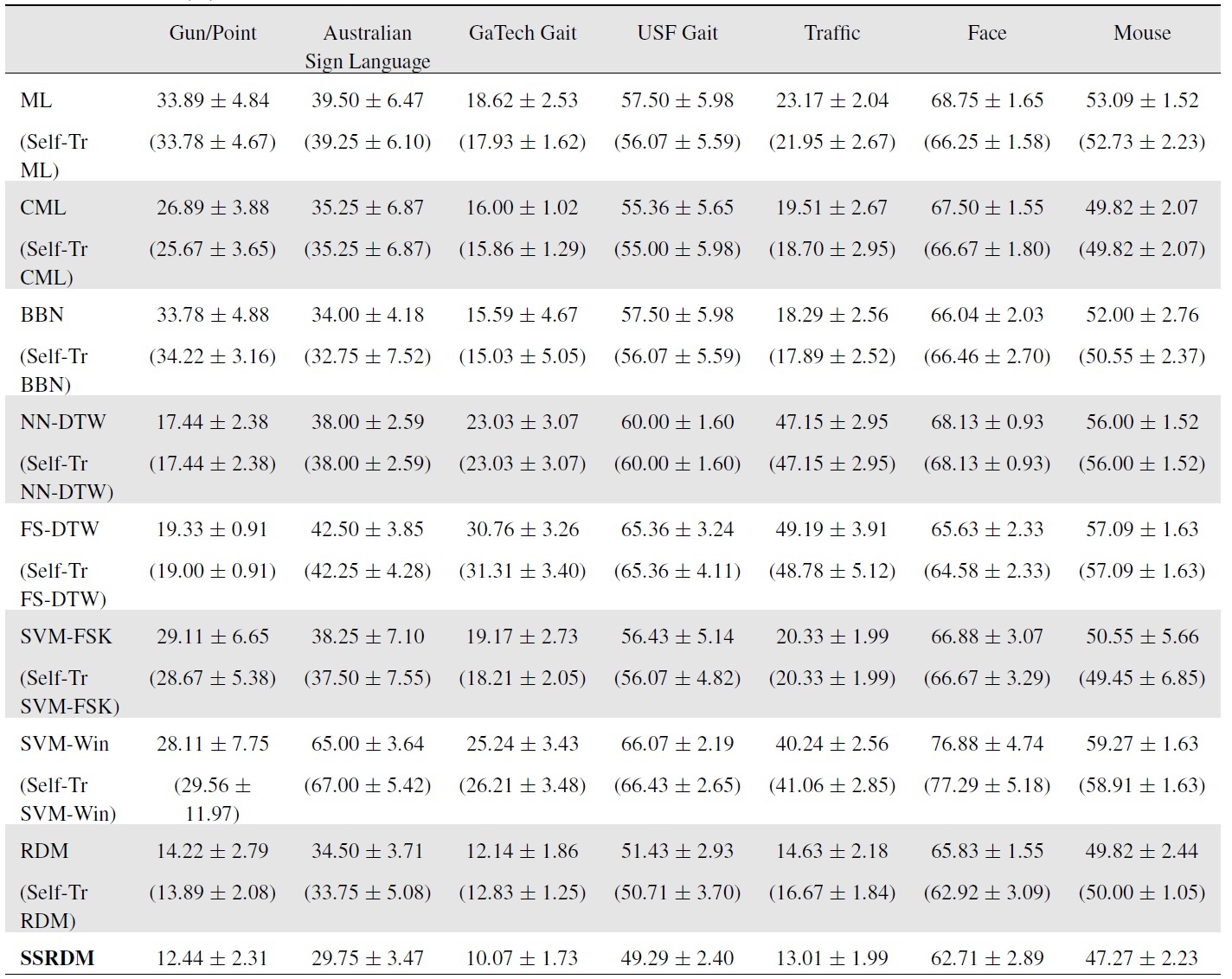
Unless stated otherwise, for the mixture/ensemble approaches (i.e., BBN, RDM, and SSRDM), the maximum number of iterations (i.e., the number of BNC components) was set to ten. The test errors for the datasets (described in the next section) are shown in Table 1.

5.2.1 Gun/Point dataset

This is a binary class dataset that contains 200 sequences (100 per class) of gun draw (class 1) and finger point (class 2). The sequences are all 1D vectors of length 150, representing the x-coordinate of the centroid of the right hand¹. This time-series dataset is a typical example where a NN approach with either a simple Euclidean distance or a DTW with small Sakoe-Chiba band size constraints works very well.

Weform five folds for cross validation with 10%/40% labeled/unlabeled training data and the remaining 50% for the test data, randomly . The sequences were pre-processed by Z-normalization so that the mean = 0 and standard deviation = 1. The GHMM order was chosen to be ten as it is also meaningful for describing 2?3 states for delicate movements around the subject’s side, 2?3 states for hand movement from/to the side to/from the target, 1?2 states at the target, and 2?3 states for returning to the gun holster.

The test errors (means and standard deviations) are shown in Table 1. NN-DTW with properly chosen Sakoe-Chiba band size (10%) outperforms ML, CML, and sequence kernel based SVM, while it is comparable to RDM. The semi-supervised learning results indicate that the SSRDM outperforms the other semisupervised methods and significantly improves on supervised

RDM by taking advantage of the large number of unlabeled data.

5.2.2 Australian Sign Language (ASL)

This UCI-KDD dataset contains about 100 signs generated by five signers with different levels of skill [31]. In this experiment, we considered 10 selected signs (“hello,” “sorry,” “love,” “eat,” “give,” “forget,” “know,” “exit,” “yes,” and “no”), forming a K = 10-way classification problem. In the original ASL dataset, each time slice of a sequence consists of 15 features corresponding to the hand position, hand orientation, finger flexion, and so on. As recommended, we ignored the 5^th, 6^th, and 11^th？15^th features. To prevent occasional noisy spikes in the original sequences, we additionally preprocessed them with a median filter. In contrast to the Gun/Point dataset, DTW is not very effective here because the lengths of sequences in the dataset are diverse, ranging from 17 to 196. We split the data randomly into 60% labeled and 20% unlabeled training data with 20% test data in five folds. For the HMM-based models, the GHMM order was chosen to be three from cross validation.

Results in Table 1 show the test errors averaged over the five test folds. The DTW with the best-chosen band constraint (B = 30) exhibits a rather poor performance, statistically indistinguishable from ML, as expected due to the large deviation in sequence lengths. Compared to ML, the discriminative approaches like CML and RDM improve the prediction accuracy considerably. Despite the small number of unlabeled data, the proposed SSRDM effectively takes advantage of them, yielding the lowest test error significantly below the random guess error rate of 90%.

5.2.3 Georgia-Tech speed-control gait database

We next tested the proposed mixture learning algorithms on the human gait recognition problem. The data of interest is the speed-control gait data collected by the Human Identification at a Distance (HID) project at Georgia-Tech. The database was originally intended for studying distinctive characteristics (e.g., stride length or cadence) of human gait over different speeds [32,33]. For 15 subjects, and four different walking speeds (0.7 m/s, 1.0 m/s, 1.3 m/s, 1.6 m/s), 3D motion capture data of 22 marked points (as depicted in [32]) were recorded for nine repeated sessions. The data was sampled at 120 Hz evenly for exactly one walking cycle, meaning that slower sequences were longer than the faster ones. The sequence length ranged from approximately 100 to 200 samples. Each marked point had a 3D coordinate, yielding 66 (= 22×3) dimensional sequences.

Apart from the original purpose of the data, we were interested in recognizing subjects regardless of their walking speeds. Taking only the first five subjects into consideration without distinguishing their walking speeds, we formulated a 5-class problem where each class consisted of 36 (= 4 speeds × 9 sessions) sequences. The original dataset provided high-quality 3D motion capture features on which most of the competing methods performed equally well. To make the classification task more challenging, we considered two modifications: (1) From the original 1-cycle gait sequence, we took sub-sequences randomly where the starting positions were chosen uniformly at random and the lengths were around 100. (2) Only the features related to the lower body part were used: the joint angles of the torso-femur, femur-tibia, and tibia-foot.

After this manipulation, we randomly partitioned the data five time into 20% labeled and 50% unlabeled training data with the remaining 30% test data. The GHMM order was chosen to be three, and the maximum number of mixture learning iterations was set to 20. As Table 1 demonstrates, the proposed SSRDM again attains the lowest errors.

5.2.4 USF human ID gait dataset

The USF human ID gait dataset consists of about 100 subjects periodically walking in elliptical paths in front of a set of cameras. We considered the task of motion-based subject identification, where the motion videos were recorded in diverse circumstances: the subject walking on grass or concrete, with or without a briefcase. From the processed human silhouette video frames, we computed the 7^th-order Hu moments that are translation and rotation invariant descriptors of binary images. The extracted features were then Z-normalized, yielding 7-dimensional sequences of duration ~ 200. While the original investigation of the set focused on how well the classifiers adapted to new circumstances (i.e., a different combination of covariates), we concentrated on identifying humans regardless of the covariates. For this, we chose seven humans from the database (a 7-class problem), each of which had 16 associated sequences containing all combinations of circumstances.

After randomly splitting the 112 sequences into 50% labeledtraining, 25% unlabeled-training, and 25% test sets five times, we recorded the average test errors in Table 1. The GHMM order was chosen to be three from cross validation. The maximum number of iterations for recursive mixture models was set to 20. Again, RDM and SSRDM have the lowest test errors with small variances, reaffirming the importance of the recursive estimation of discriminative mixture models when combined with the use of unlabeled data.

5.2.5 Traffic dataset

We next tackle a video classification problem that has demonstrated the utility of dynamic texture methods [34,35] in the computer vision community. Dynamic texture is a generative model that represents a video as a sample from a linear dynamical system. Dynamic texture can extract the visual or spatial components in the image measurements using PCA while capturing the temporal correlation by the latent linear dynamics. Hence, a video, potentially of varying length, can be succinctly represented by two matrices (A, C), where A is the dynamics matrix on the low-dimensional latent space, and C is the emission matrix that maps the latent state to the image observation. To apply dynamic texture to the video classification problems, the Martin distance [34] is often employed. It defines the similarity measure (or kernel) between a pair of videos based on the principal angles between subspaces represented by their matrix parameters. Once the distance measure is estimated, one can readily employ standard classifiers such as nearest neighbors or SVMs.

The dataset we used in this experiment is traffic data (also used in [36]) that contains videos of highway traffic taken over two days from a stationary camera. The videos were labeled manually as light, medium, and heavy traffic, posing a 3-class problem. The videos are around 50 frames long, where each image frame is of size (48 × 48), yielding a 2304-dimensional vector.

For the dynamic texture approach, we set the latent space dimension to be eight. We used the same dimension for our GHMM-based competing approaches, where we used the PCA dimension-reduced observation in the GHMMs. We collected 131 videos (with a nearly equal number of videos for each class), and randomly split them into 60% labeled-training, 10% unlabeled-training, and 30% test sets five times. The GHMM order was chosen to be two, and the maximum number of iterations for recursive mixture models was set to 20. The SVM classifier with the Martin distance measure estimated from the learned dynamic texture recorded a test error of 16.67 ± 1.84%, outperforming many of the competing approaches as shown in Table 1. However, the proposed SSRDM (and RDM) achieved still higher prediction accuracies than the dynamic texture model.

5.2.6 Behavior recognition

Finally, we deal with a behavior recognition task, a very important problem in computer vision. We used the facial expression and mouse behavior datasets from the UCSD vision group¹. The face data are composed of video clips of two individuals, each displaying six different facial expressions (anger, disgust, fear, joy, sadness, and surprise) under two different illumination settings. Each expression was repeated eight times, yielding a total of 192 video clips. We used 96 clips from one subject (regardless of illumination conditions) as training data, and predicted the emotions of other subjects in the video clips (a 6-class problem). We further randomly partitioned the training data into 50% labeled and 50% unlabeled sets five times. The mouse data contained videos of five different behaviors (drink, eat, explore, groom, and sleep). From the original dataset, we formed a smaller set comprising 75 video clips (15 videos for each behavior). We then randomly split the data into 25% labeled training, 40% unlabeled training, and 35% test sets five times.

In both cases, from the raw videos, we extract the cuboid features of [37] that are spatio-temporal 3D interest point features. Similar to [37], we constructed a finite dictionary of descriptors, and replaced each cuboid descriptor by a corresponding word in the dictionary. More specifically, we collected cuboid features from all training videos, clustered them into C centers using the k-means algorithm, and replaced each cuboid by its closest center ID.

For the classification, we first ran the static mixture approach in [37] as a baseline, where they represented a video as a histogram of cuboid types, essentially forming a bag-of-words representation. They then applied the nearest neighbor prediction using the χ² distance measure over the histogram space. Setting C = 50 with other cuboid parameters properly chosen, we obtained test errors of 68.75 ± 2.95% for the face dataset and 52.36 ± 0.81% for the mouse dataset. (Note that random guessing would yield 83.33% and 80.00% error rates, respectively.)

Instead of representing the video as a single histogram, we considered a sequence representation for our GHMM-based sequence models. For each time frame t, we collected all cuboids that spread over t and formed a histogram of cuboid types for it. Hence, we formed a C-dimensional histogram feature vector for each time slice t, where we used GHMMs to model the nonnegative quantities (histograms). Note that some time slices did not contain any cuboids, in which case the feature vector was a zero-vector. To avoid a large number of parameters in GHMM learning, we further reduced the dimensionality of the features to five dimensions with PCA.The test errors of the competing approaches for this sequence representation are recorded in Table 1. Here the best GHMM orders are three for the face dataset and four for the mouse dataset. For both cases, our discriminative recursive mixture learning algorithms (RDM and SSRDM) consistently exhibited the best performance within the margin of significance, outperforming [37]’s baseline method .

The experimental results for the semi-supervised classification settings imply that SSRDM is significantly better than selftraining. This can be attributed to the SSRDM’s effective and discriminative weighting scheme that discovers the most important unlabeled data points for classification. Compared to our SSRDM, the performance improvement achieved by the self-training algorithm is small and can sometimes deteriorate classification accuracy.

1Selecting the number of hidden states in GHMMs is an important task of model selection that we accomplish using cross validation.

1Alternatively, one can directly tackle multi-class problems via multiclass SVM [27]. The other possibility in binarization is the one-vs-one treatment [28,29]. In our evaluation, however, WTA in one-vs-others settings slightly outperforms these two alternatives almost all the time, hence we only report the results of WTA.

1For further details about the data, please refer to [30].

1Available for download at http://vision.ucsd.edu.

In this paper we have introduced a novel semi-supervised discriminative method for learning mixtures of generative BNC models. Under semi-supervised settings, we utilized the minimum entropy principle leading to stage-wise data weight distributions for both labeled and unlabeled data. Unlike traditional approaches to discriminative learning, the proposed recursive algorithm is computationally as efficient as learning a single BNC model while achieving significant improvement in classification performance. Our recursive mixture learning is amenable to a pre-determined mixture order as well as robust to the choice of initial parameters.

No potential conflict of interest relevant to this article was reported.