In real-world application, several practical situations can be modeled using nonlinear optimization problems with system equilibrium constraints, including complementarity conditions [1-3]. In optimization problems, complementarity constraints (CCs) are used to explain the disjunctive condition of system models [4]; that is, depending on a given environment, different rules are imposed for systems with these constraints. They can be found in mechanics, circuits with electronic switching devices, structural studies, and power market models in the electricity industry [1,2,5].
In the past decades, many research activities on the application of interior point methods (IPMs) to nonlinear programming, one of the diverse engineering problems, have been conducted [6-10]. IPM adopts the log-barrier penalty functions to adequately cope with inequality constraints; it was first proposed by Frish [11]. The IPM presented by Karmarkar [12] was designed for linear programming problems, and it was considered to be approximately 50 times faster than the common simplex method. Later, IPMs were devised [6,7,13,14], which can find solutions to primal and dual variables. The current paper mainly discusses the methods for dealing with complementarity conditions in primal and dual nonlinear IPMs (NIPMs).
The standard complementarity problems find solutions to the following conditions:
where the operator of the last condition in (1) denotes the inner products. In [15], a method of formulating generalized complementarity problems with an unconstrained optimization problem was discussed. From the result, an optimization problem with complementarity conditions was envisaged to be reformulated into a multi-objective optimization problem. For practical NIPM applications, a set of reduced correction equations is usually adopted, including the Hessian term and the Jacobian sub-matrix, only for the equality constraints [16,17]. Thus, if the equality formulation of (1) is added to the NIPM formulation, the system size of the correction equations must be increased; hence, a certain amount of effort is required for modification of the CC.
The present paper presents a method of fuzzy-enforcing CC as a form of inequality for NIPM-based optimization methods. Fuzzy enforcement was originally proposed in [18], but it was designed for general equality and inequality constraints in successive linear programming algorithms. By introducing fuzzy enforcement, the method proposed in this paper can adequately deal with the concept of “not too much” violation of the complementarity conditions, providing enough room for the solutions to approach optimality. This paper also presents the numerical results when the method was applied to an NIPM-based optimal power flow (OPF) with CCs in the generator voltage and reactive power generation.
The formulation of nonlinear programming problems in this study with the CC of interest can be briefly expressed as follows:
where
On the basis of the condition where the CC factors are nonnegative,
the equivalent inequality constraint can be expressed as follows:
When NIPM is applied to the optimization problem using this inequality form of the CC, using the same dimensional correction equations as those of the nonlinear optimization problem is possible without the equality form of the CC. However, NIPM employs the log-barrier functions to force the solution in the whole procedure within the feasible region; hence, the solution cannot move from the initial vector of
2.2 Fuzzy Enforcement of the CCs
We let the
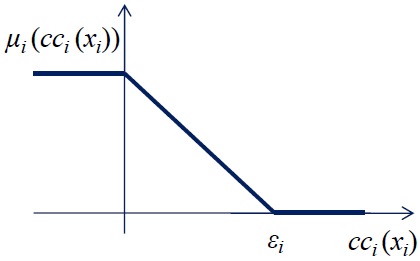
Each fuzzy relation in the fuzzy set theory is associated with a membership function that represents the degree of certainty. The membership function in (4) can be expressed as follows (Figure 1):
where
To apply the fuzzy-enforced CC to the optimization problem, the degree of satisfaction in the NIPM solution process should be enhanced. For this purpose, the optimization problem can be rewritten with a multi-objective function as follows:
where
The second term of the objective function in (6) forces each
To solve the nonlinear optimization problem in (6), this study adopts the NIPM [7,17] using the fuzzy-enforced CCs. NIPM is a Newton-type approach to nonlinear programming problems, but the introduction of log-barrier functions for the inequality constraints facilitates the dealing of these constraints. In addition, a step size of each solution process is selected to force the solution within the feasible region; thus, deciding the set of active inequality constraints, which is usually needed in Newton-type approaches, becomes unnecessary.
As mentioned in subsection 2.1, the two CC factors are nonnegative. Therefore, the lower limit of
When
For the NIPM application, the problem formulation can be modified as follows:
where
When the log-barrier functions are considered for the remaining inequality constraints of the slack variables, the Lagrange function can be constructed as follows:
where
2.4 Implementation of fuzzy enforcement of CCs on OPFs
In this study, the fuzzy enforcement of a CC was applied to the problem of generator voltage and reactive power generation in the formulation of the OPF. The CC in the OPF formulation can be expressed as follows:
where
The OPF formulation must satisfy only (10) or (11), that is, when the CC in (10) is taken into account, that of (11) should not be included in the formulation. Even though the above CC must be considered, the conventional OPF does not include the CC for the generator voltage and the reactive power generation. In this study, fuzzy enforcement is adopted for the CC in (10) and (11), and the NIPM process decides which CC is to be incorporated into the formulation.
This section presents an illustrative example using an island power system. The system includes nine in-service generating units, three wind turbine generators, battery energy storage systems (BESSs), and two high voltage direct current (HVDC) interties from external electric network systems to support the electricity consumption level of the system. In the simulation, we assume that the active and reactive power injections from the HVDC interties are fixed. Further, the wind turbine generators are considered as conventional generators with reactive power capability. The voltage stability issues of the Jeju system were described in [20].
In the present study, the fuzzy-enforced CCs for the generator voltages and reactive power generation are implemented on a modified version of the NIPM-based OPF in [17]. In the simulation, the objective function of the OPF is to minimize the total loss in the transmission lines. In the commonly used OPFs, the control vectors are the desired voltage magnitudes of the generators. However, the target of the OPF proposed in this paper is to determine the reactive power output of the
BESS without any changes in the generator terminal voltages. The current control settings of the generator voltages can be maintained by considering their CCs, as expressed in (9) and (10). To reduce the transmission loss, only the reactive power output of the BESS in the power system is allowed to move as control vectors.
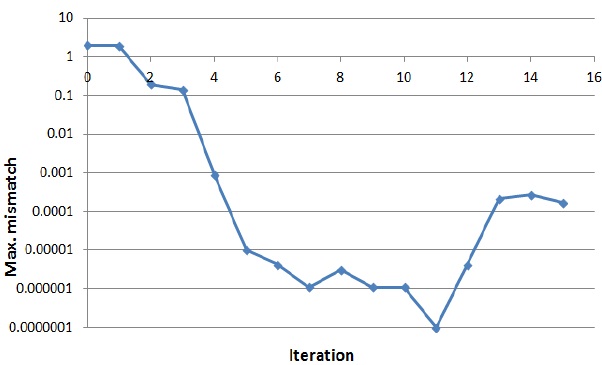
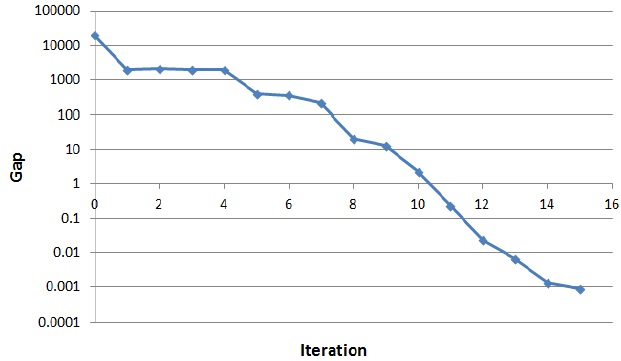
For the island power system, the NIPM-based OPF with the fuzzy-enforced CC for the generators was performed. The process took 16 iterations until the solution satisfied the stopping criteria. The maximum allowable mismatch for the equality constraints was 102, and the tolerance of the complementary gap for the primal and dual variables in the simulation was 10?3. Figures 2 and 3 show the change in the complementary gap and the maximum mismatch of the network constraints, respectively.
Figure 2 shows that the complementary gap is gradually reduced until it becomes less than the tolerance. The centering parameter [16] of the NIPM is set to 0.1, and hence, we can expect the complementary gap to reduce by 90%. Figure 3 shows that in the initial part of the solution process, the maximum mismatch is dramatically reduced below the solution tolerance, but in further iteration, the maximum mismatch increases to
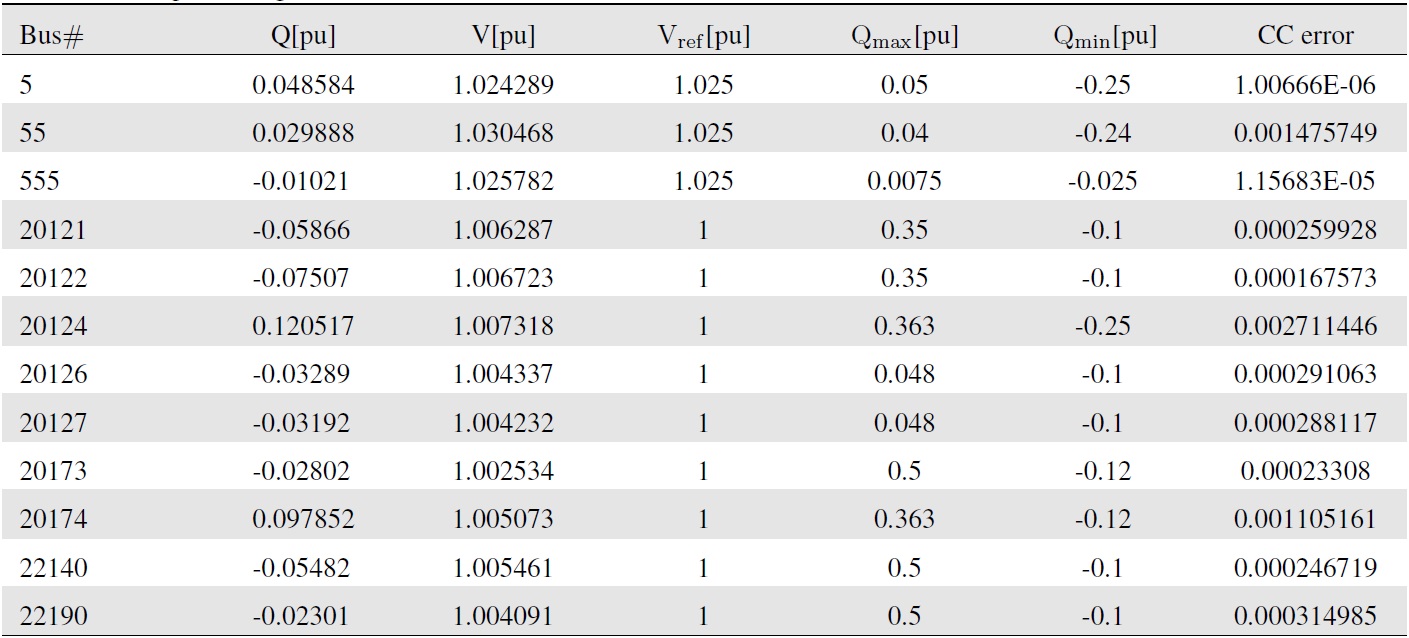
[Table 1.] QV output of the generators at the final solution
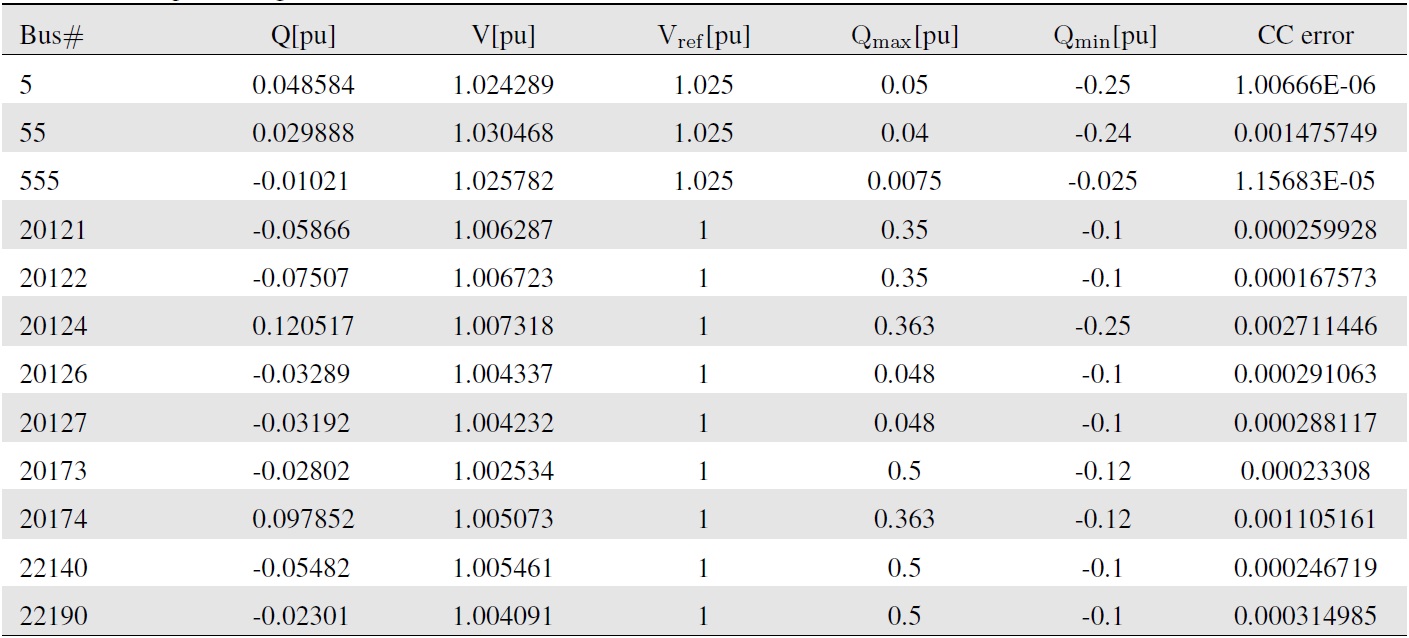
QV output of the generators at the final solution
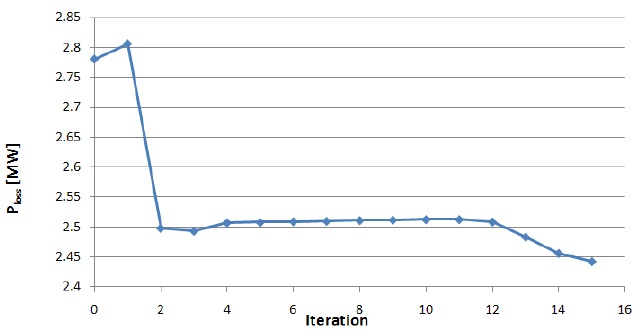
some extent and then decreases below the tolerance. This phenomenon might have stemmed from the application of the CCs for the voltage?reactive power relationship. The same situation applies to the change in the active power loss up to the 12th iteration. When the final solution is obtained, the transmission loss is 2.4429 [MW]. Figure 4 shows the change in the active power loss during the solution iteration.
Table 1 shows the reactive power and voltage magnitudes of each generator at the final solution and the corresponding CC values. The CC of the generator at bus 5 is related to the maximum reactive power limit, as expressed in (10), and those of the other generators are related to the minimum reactive power limit, as expressed in (11). At the final solution, the CC errors of the generators are different, and the total CC error is approximately 0.007106 [pu], as shown in the last column in Table 1. This CC error appears to be acceptable from the engineering point of view.
This paper has presented a fuzzy set method for enforcing CC in an NIPM-based optimization. NIPM is a Newton-type approach to nonlinear programming problems, but it adopts the log-barrier functions to deal with the obstacle of managing inequality constraints. The fuzzy-enforcement method has been implemented for CCs, which can be incorporated in optimization problems for real-world applications. In this paper,
numerical simulations that apply the method to power system OPF problems have been included.
No potential conflict of interest relevant to this article was reported.