Optical receivers are basic building blocks in various kinds of optical communication systems. To increase the transmission distances, optical receivers suffer from various electrical and optical noises. In early optical communication systems, shot and thermal noises limit the receiver performances dominantly [1,2]. After the appearance of optical amplifiers, the amplified-spontaneous emission (ASE) becomes the most dominant noise source that mixes with the optical channel at the photo-detector [3-5]. For the analysis of optical receivers in the presence of the ASE, there are exact methods using receiver eigenmodes in the time domain [6-9] and in the optical spectral domain [10-13]. The time domain analyses have been developed initially for radiofrequency receivers.

Conventional analyses find the receiver eigenmode contributions at a specific time where the decision is made. Actually, the receiver eigenmode contributions change as a function of time within a bit period. These behaviors are affected by the optical and the electrical filters within the optical receiver. Accordingly, the distribution of the electrical voltage after the electrical filter will undergo similar changes within a pulse. Until now, however, no time-dependent analysis has been performed yet which is important for understanding the physics of optical receivers.

In this paper, we provide a time-dependent analysis of optical receivers whose optical inputs are corrupted by the ASE. We use the receiver eigenmodes in the optical spectral domain. Our analysis explains the physics about the receiver output signal and noise distributions as a function of time using receiver eigenmodes. We choose Gaussian optical receivers [14] that are good approximations to practical optical receivers yielding quantitative results with closed-form eigenfunctions.

We assume the optical receiver has an optical filter in front of a photo-detector to select an optical channel and also to filter out the ASEs from optical amplifiers. After the photo-detector, there is a low-pass electrical filter to filter out high frequency electrical beat noises.

For simplicity, we neglect the polarization component perpendicular to that of the received signal. It will be included as an additive term after the signal contributions are fully evaluated. Just before the optical filter, the complexelectric- field amplitude is denoted as ε_in(ω) in the optical frequency domain. After the optical filter, the complexelectric-field amplitude is ε_out(ω)=ε_in(ω)H_o(ω), where H_o(ω) is the optical filter’s transmittance for the complex-electricfield amplitude. After the optical detection, the photo-detector output current is (k/2)| E_out(t)|², where k is a proportional constant and E_out(t) is the inverse Fourier transform of ε_out(ω). After the electrical filter having a transfer function of H_e(ω), we have the voltage waveform at the output of the electrical filter as

where the kernel K(ω,ω') is given by

We expand ε_in(ω)exp(jωt) in (1) as

where ？_m(ω) is the eigenfunction of the m-th receiver eigenmode and V_m(t) is its expansion coefficient. The eigenfunctions satisfy the second kind of homogeneous Fredholm integral equation

λ_m is the eigenvalue of the m-th receiver eigenmode. The eigenvalues are real since the kernel is Hermitian. The eigenfunctions satisfy the orthonormal relation

where the asterisk symbol represents the complex conjugation.

Using (3) for (1), y(t) can be simplified greatly as a summation of receiver eigenmode contributions

The amplitude of the m-th eigenmode V_m(t) can be decomposed into signal and noise components denoted as S_m(t) and N_m(t), respectively, as

Without loss of generality, we may set t = 0 in (3). Then we have

The inverse Fourier transform of (7) gives

where ψ_m(t) is

times the inverse Fourier transform of ？_m(ω) and also satisfies the orthonormal relation in time domain

Inserting (7) into (3), we find

From this relation, V_m(t) is found as

where C_km(t) is a correlation function

Equation (12) shows that the expansion coefficient set {V_m(t)} at t≠0 can be found from {V_m(0)} with m= 0, 1, 2...

Multiplying both sides of (3) with their complex conjugates and integrating over ω, we obtain [14]

Equating the signal parts from both sides of (14), we have

where ε_in,s(ω), is the signal part of ε_in(ω). It means that the sum of |S_m(t)|² is a constant proportional to the total signal energy assumed to be finite here. Note that (15) holds independent of time. Thus, if the amplitude of a dominant eigenmode decreases, the amplitudes of other eigenmodes increase making the sum of |S_m(t)|² over m unchanged.

If the other polarization component of the received channel is included, (5) may be rewritten as

where we have used a prime notation for the contributions from the newly added polarization component. The polarization vector for the second term of (16) has only noise components and V'_m(t)=N'_m(t). All the real and imaginary parts of {N_m(t)} and {N'_m(t)} at a fixed time are mutually independent Gaussian random variables with zero mean and an identical variance of

[10].

In dense wavelength-division multiplexing (DWDM) systems [15,16], the optical filter’s bandwidth is comparable to the modulation bandwidth. In this case, the magnitude of the eigenvalue λ_m increases rapidly as m increases from zero [10,14]. This can be understood by the decrease in the freedom of mixing between optical frequency components in DWDM systems. As a result, the first term of (16) will be dominant as long as |S₀(t)|>>|S_m (t)| for m≠0 such that

If we use ψ₀(t) for a single mark signal transmission, it means V_m(0)=0 for m≠0. ψ₀(t) has a single maximum and the corresponding lowest-order eigenfunction in the spectral domain ？₀(ω) occupies the smallest bandwidth of all eigenfunctions. We can prove that, in this case, the signal-to-noise ratio is maximized at t = 0 [14] and the decision time should be chosen here to have the voltage

In DWDM systems, (18) may be approximated as

It is straightforward that the probability distribution function (pdf) of y(0) from (19) has a non-central chi-square distribution [17,18]. As |t| increases from zero, higher-order receiver eigenmode contributions to y(t) increase from the relation S_m(t)=S₀(0)C_0m(t). At the same time, the magnitude of S₀(t) decreases since the total sum of |S_m(t)|² is conserved as

Therefore, according to the central-limit theorem [19], the pdf of y(t) becomes closer to Gaussian as the number of non-negligible or contributing eigenmodes increases. Note that the pdf of y(0) becomes more symmetric also when its mean value increases. If we use pulses somewhat different from ψ₀(t) to send a mark signal, normally a small number of eigenmodes would contribute to y(0) from the lowest order and the pdf of y(t) would resemble the Gaussian more closely. These behaviors can be explained more quantitatively using Gaussian optical receivers.

We use Gaussian optical receivers [14] for our time-dependent analysis since they are good approximations to various optical receivers and have closed form eigenfunctions. We will show that, when the received optical pulse is a Gaussian pulse, the electrical pulse after the electrical filter is also a Gaussian pulse. Then our results will be compared with our foregoing time-dependent analysis.

The optical filter of a Gaussian optical receiver has a Gaussian impulse response as

where t_o is the time delay of the optical filter. h₀(t) is the inverse Fourier transform of H_o(ω). Also, the electrical filter of a Gaussian optical receiver has a Gaussian impulse response

where t_e is the time delay of the electrical filter. The 3-dB bandwidth of |H_o(ω)|² is

Similarly, the 3-dB bandwidth of |H_e(ω)|² measured from the origin is

The Gaussian receiver’s eigenfunction ？_m(ω) is given as a Hermite function times exp(jωt_d) as follows:

where, t_d(=t_o+t_e) is the total time delay of the receiver. H_m(ω/a) is the Hermite polynomial. The 3-dB bandwidth of |？₀(ω)|² is

The parameters, a, α, and β, are related as α² =a²(1+q)/(1？q) and β² =a²(1？q²)/2q, where q is a positive quantity less than 1 given by

r = 2α/β is the 3-dB bandwidth ratio of the optical and the electrical filters. Note that the Fourier transform of the Hermite function is also proportional to a Hermite function. Thus we have

The corresponding eigenvalues are given as

where H_c|H_o(0)|²H_e(0).

We assume the received signal is a Gaussian pulse without the ASE such that

where b is a constant. Then its Fourier transform is

and the 3-dB bandwidth of |ε_in(ω)|² is

When b = a, E_in(t) is proportional to ψ₀(t). From (7), we find

In particular, we have for m=0

The E_out(t) after the optical filter is found as

The photo-detector output current is (k/2)|E_out(t)|². The output voltage of the electrical filter can be evaluated exactly as follows:

The output waveform of the Gaussian receiver for the Gaussian input (25) is also a Gaussian with its maximum at t = 0.

From (5), the output of the Gaussian receiver has the following expression:

Comparing (30) with (31), we can find the receiver eigenmode contributions at arbitrary times. For example, setting t=0, where the output voltage of the Gaussian receiver is maximized, we may expand y(0) obtained from (30) as a Taylor series about the q=0 point except the

factor

Only the even eigenmodes contribute and the lowest-order eigenmode (m = 0) contribution becomes dominant when q is much less than 1. In particular, when b=a, only the lowest-order mode term is present at y(0) independent of the q value.

We can find the lowest-order mode contribution to y(t), denoted as y_L(t), after setting q=0 except the

factor,

The ratio between y_L(t) and y(t) is

This ratio has a maximum at t = 0 where the signal is also maximized. In other words, the contribution of the lowest-order eigenmode is maximized at the pulse center t = 0. It decreases as |t| departs from zero and higher-order eigenmode contributions increase. The lowest-order eigenmode contribution also decreases as q increases. When b=a, we have y_L(t)/y(t) = exp(-qa²t²/2). There are no higher-order eigenmode contributions at t = 0 irrespective of q or r.

The correlation functions for the Gaussian optical receiver can be derived as

where

is the associated Laguerre polynomials [20]. Especially, when k = 0, we have

When b = a, (30) reduces to

Comparing (38) with (31), we find

This result matches with (37).

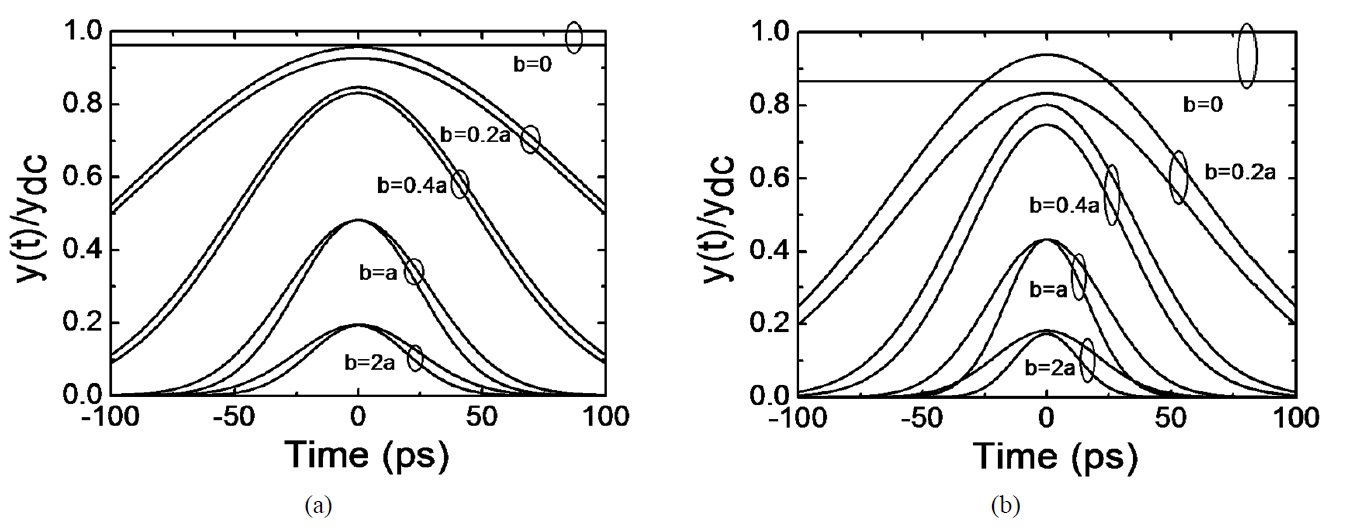
In Fig. 1(a), we plot y(t) and y_L(t) for r = 2 (q = 0.268) for several b values. y(t) and y_L(t) are normalized by y_dc which is the dc response of y(t) with b=0. Between the two traces for a given b value, the lower one corresponds to y_L(t). At b=0, the signal is unmodulated and about 4% of y(t) is the contributions from higher-order eigenmodes. As b increases from zero to a, the higher-order eigenmode contributions decrease to zero at t=0, where the signal power is maximized. When b=a, only the lowest-order eigenmode contributes or y(0)=y_L(0) As b increases further from a, the contributions of higher-order eigenmodes increase at t=0 but more slowly. In Fig. 1(b), we use r=4 (q=0.5). At

b=0, about 13% of y(t) belongs to higher order eigenmodes. Overall, the higher-order eigenmode contributions are larger than Fig. 1(a). When b=a, only the lowest-order eigenmode contributes at t=0 as Fig. 1(a).

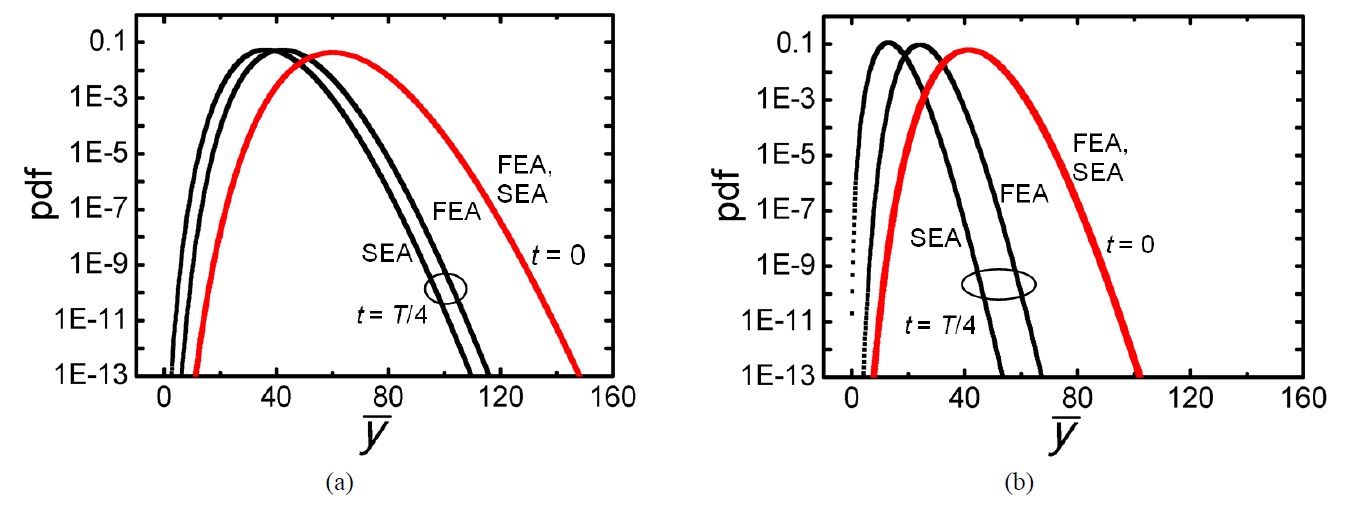
In Fig. 2(a), we show the pdfs of ？(t)=y(t) / y_sp for b=a and for r=2 (q=0.268) at t=0 and T/4. T is the bit period chosen to be 100 ps assuming the bit rate as 10 Gb/s. y_sp is the average value of y(t) per polarization in the absence of the signal given as

We have set A₀(0)=81.3 and A_m≠0 that gives 10^-9 bit-error rate at t=0 [14]. The pdfs are found as an inverse Fourier transform of the characteristic function of y(t) [10]. We have used 30 eigenmodes in the full eigenmode analysis (FEA) and used only the lowest-order eigenmode for the single-eigenmode analysis (SEA). We have chosen

as 7 GHz. At t=0, the FEA and the SEA give almost the same pdfs, which means the effects from {N_m≠0(0)} are negligible. At t=T/4, the FEA gives more symmetric pdf with respect to its peak than that of the SEA. Note that the pdf at t=0 is more symmetric than the pdf obtained by the FEA at t=T/4. We show in Fig. 2(b) the pdfs of ？(t) for r=4 (q=0.5) with all other conditions the same as Fig. 2(a). In this case, as Fig. 1 shows, higher order eigenmodes become more important at t=T/4 than Fig. 2(a). At t=0, the FEA and the SEA still give almost the same pdfs. At t=T/4, the FEA gives more symmetric pdf than the SEA. The pdf at t=0 has a similar symmetry with respect to its peak as the pdf obtained by the FEA at t=T/4.

We have analyzed the time-dependent behaviors of optical receivers corrupted by the ASE using receiver eigenmodes. The correlation functions between receiver eigenmodes in time domain determine the amplitudes of eigenmodes at different times. Gaussian optical receivers are used for our analysis that have Gaussian optical and electrical filters with closed-form receiver eigenfunctions. The edge parts of the Gaussian electrical pulse have larger contributions of higher-order eigenmodes than the pulse center where the lowest-order eigenmode is dominant. This effect is dependent on the bandwidth ratio between the optical and the electrical filters as well as the input pulse’s time width. It is enhanced when the time-width of the received Gaussian optical pulse decreases or when the bandwidth ratio increases. According to the central limit theorem, as the number of contributing eigenmodes increase, the voltage distribution of the electrical pulse at that instant becomes more symmetric and close to Gaussian. Our analysis explains the time-dependent signal and noise properties within the electrical pulses at the output of the receiver electrical filter. For Gaussian optical receivers, we have shown that the best decision time is at the peak of the electrical pulse. For other cases of non-Gaussian filters and of non-Gaussian input pulses, our analysis can be used also to get the best decision timing.