Due to the ability to provide a dispersive spectroscopic lineshape, polarization spectroscopy (PS) [1] has been widely used and studied in particular for laser frequency stabilization. In PS, a circular birefringence is established by a circularly polarized pump beam. This is detected by measuring the rotation angle of a linearly polarized probe beam propagating in the opposite direction to the pump beam. The sub-Doppler feature originates from the fact that only the atoms belonging to certain velocity classes can experience the pump and probe beams simultaneously. The atoms with zero velocity contribute to the resonance signals, whereas the crossover signals result from the contribution from the atoms satisfying the condition that the frequency spacing of the excited state is equal to twice the Doppler shift.

PS has been realized for many kinds of atoms such as Li [2], Rb [3-6], Cs [6,7], K [8], He [9], and Sr [10]. In the case of all the atoms except for Sr, the PS spectra result from three operating mechanisms such as Zeeman and hyperfine optical pumping and the saturation effect. In contrast, the PS for Sr results from only the saturation effect because there are no degenerate sublevels in the ground state. Since the isotopes ⁸⁴Sr, ⁸⁶Sr, and ⁸⁸Sr possess zero nuclear spin (I = 0), whereas ⁸⁷Sr possesses I = 9/2, the J_g = 0 → J_e = 1 transition exists in the isotopes ⁸⁴Sr, ⁸⁶Sr, and ⁸⁸Sr. In this paper, we will consider ⁸⁸Sr. In addition, Yb isotopes with mass numbers, 168, 170, 172, 174, and 176, also possess zero nuclear spin. Because the energy level structure of Sr (and Yb) is very simple, it is possible to obtain exact analytical solutions for the PS spectra. The analytical solution of saturated absorption spectroscopy (SAS) for the ideal two-level atoms was presented in the textbook [11]. Also, SAS [12] and PS [13] for Rb atoms were analytically studied in the low intensity limit. In this paper, we present analytical solutions of PS for the transition J_g=0→J_e =1 of Sr (or Yb) atoms where the intensity of the pump beam is arbitrary. This paper is organized as follows. Section II describes the theory of calculating analytical lineshape in PS. Results and discussion are presented in Sec. III. The final section summarizes the results of the paper.

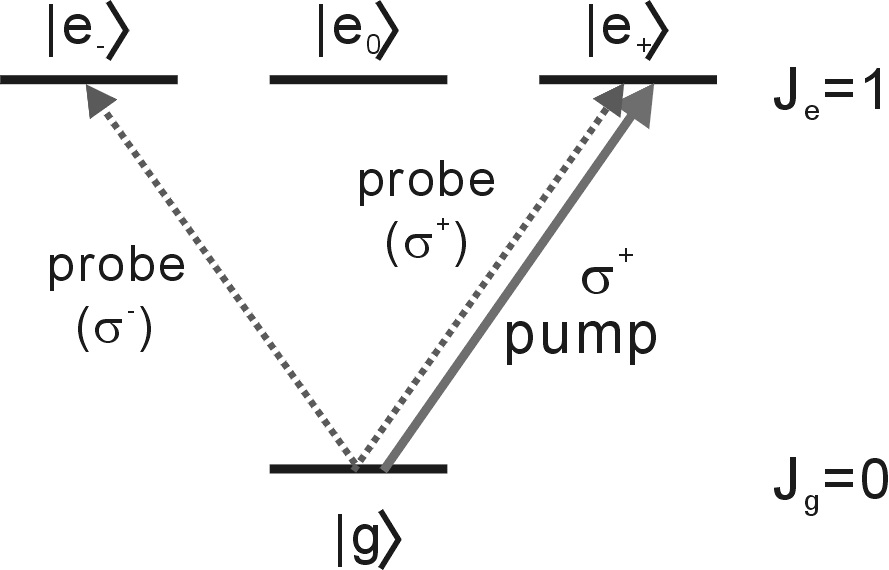
The energy level diagram for the transition J_g=0→J_e =1 of an atom (⁸⁸Sr or Yb) is shown in Fig. 1. The ground state is |g>, while three degenerate excited states are |e_？>, |e₀>, and |e₊> where magnetic quantum numbers are -1, 0, and 1, respectively. The pump beam of σ⁺ polarization excites the transition from |g> to |e₊>, whereas the linearly polarized probe beam excites both the transitions from |e> to |e_±>. ω₀ is the resonance frequency, λ is the wavelength, k = 2π/λ is the wave vector, Ω₁₍₂₎ are the Rabi frequencies for the pump (probe) beam, Γ is the

decay rate of the excited state, and γ_t is the decay rate of the optical coherence which is equal to Г/2 if there is no dephasing mechanism. The laser frequencies of the pump and probe beams felt by an atom moving at velocity, v, are ω₁ =ω + kv and ω₂ =ω ？ kv, respectively.

Then, the susceptibilities of the σ^± components of the probe beam for an atom moving at velocity, v, are given by [14]

where p denotes the population of the ground state, q± denotes the populations of the excited states, |e_±>, and N_at represents the atomic density. The populations in Eq. (1) are calculated analytically by considering the effect of only the pump beam. Since the σ⁺ polarized pump laser field couples only the ground state and the excited state (|e_±>), we can use the results for the case of a two-level atom. Thus, we refer to our previous result [14] or a textbook [15], and the results are given by

and q₀ = q_？ = 0, where A = (ω₁ - ω₀)² +γ_t² and B =Ω₁²γ_t/Γ.

Therefore, the susceptibilities in Eq. (1) become the following equations:

Equations (2) and (3) are then averaged over the Maxwell- Boltzmann velocity distribution a

where u is the most probable speed of the atom. Equation (4) is further simplified by changing the integration variable as

where

and δ(=ω ？ω₀) is the detuning and s₀(=Ω₁²/γ_tΓ)=I₁/I_s is the on-resonance saturation parameter where I₁ is the pump beam intensity and I_s = πhcΓ/(3λ³) is the saturation intensity with c being the speed of light in vacuum. The integration in Eq. (5) can be easily performed using a convolution theorem. When γ_t≪ku, the real and imaginary parts of the susceptibilities are given by

respectively.

In PS, a linearly polarized probe beam (intensity is I₀ and polarization vector is

is incident on an atomic cell of length l along the z axis. After traversing the cell, the polarization of the probe beam changes due to the circular anisotropy from the pump beam. The electric field of the probe beam is then given by [5,14]

where E₀ is the amplitude of the incident probe beam’s electric field, a_± = e^-(k/2)χi±l, and n_± ？ 1+(χ_±/2) are the refractive indices of the σ^± components of the probe beam.

are the spherical bases where

are the unit vectors for x and y axes, respectively. The inclination angle of the electric field in Eq. (6) with respect to the x axis is given by θ + ？ where θ is the inclination angle of the incident probe beam’s polarization and ？=(kl/2)(n_--n₊) ？ (kl/4)(χ_-^r-χ₊^r)is the rotation angle of the probe beam's polarization after traversing the atomic cell [16]. Then, the difference in the intensities along the x and y axes, ΔI = I_x ？ I_y, is given by

ΔI = I0a+a_cos[2θ+2？],

and becomes further

ΔI = I0a+a_sin2？,

when θ =π/4. Since the rotation angle, ？, is very small, the PS signal is given by

where

is the average of the absorption coefficients. The difference in the real parts of the susceptibilities (Δχ^r ≡ χ_？^r？χ₊^r) is given by

where

We neglect e^？δ2/(ku)2 in Eq. (8) because |δ| ≪ku.

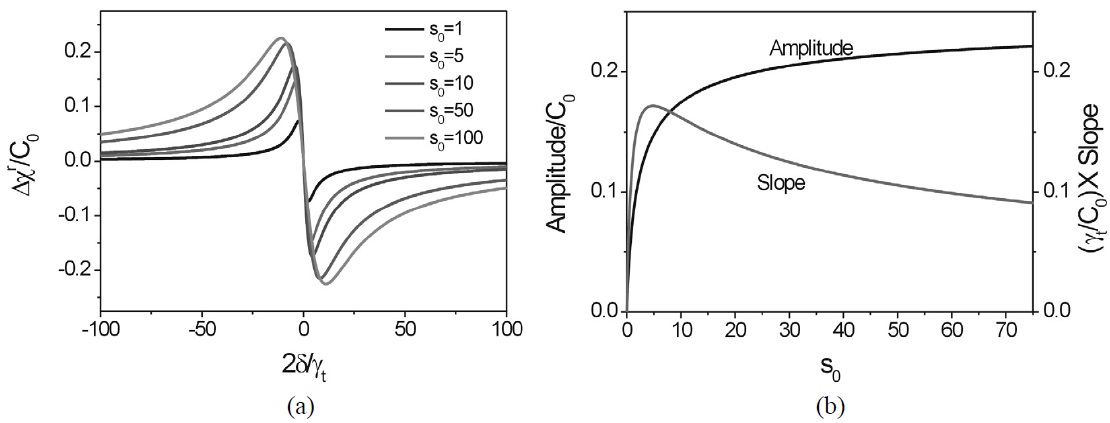
The typical PS spectra (Δχ^r) for several pump beam intensities are presented in Fig. 2(a). In Fig. 2(a), the saturation parameters were s₀ = 1, 5, 10, 50, and 100. The saturation parameter of s₀ = 100 corresponds to the intensities of 4.27 W/cm² because the saturation intensity of Sr atom is about 4.27×10^-2 W/cm². The amplitude of the spectrum, defined as |Δχ^r| at x=±1, and accordingly at the detunings of

is given by

and the magnitude of the slope of the PS spectrum at the resonance condition is given by

The calculated amplitude and slope as functions of s₀ are presented in Fig. 2(b). In Fig. 2(b), the amplitude increases and is then saturated at the value of C₀/4. In Fig. 2(b), the slope is maximum when

This value corresponds to the intensity of 0.206 W/cm². This is in excellent agreement with the experimental results in Fig. 4(b) in Ref. [10].

In this paper we have presented a theoretical study of lineshape in PS for the transition J_g=0→J_e =1 of Sr atoms. Equations (7) and (8) are the main result of the paper. The amplitude and the slope of the spectrum are presented in Eq. (9) and Eq. (10), respectively. The theoretical results were compared with experimental results presented in Ref. [10], and excellent agreement between them was found. Since the obtained results in this paper are very concise, these can be applied to study of PS for other atoms such as Yb and to study of other spectroscopy such as sub-Doppler dichroic atomic vapor laser lock (DAVLL) [10].