In 1968 Veselago proposed that simultaneously negative permeability and permittivity in an isotropic material leads to negative refractive index. According to this fact that the pointing vector and wave vector in these materials are in opposite directions, he called them left-handed materials (LHMs) or negative index materials (NIMs) [1]. As an electromagnetic (EM) wave passes the border between a medium with positive refractive index and a LHM, the beam of light would be refracted to the same side of the normal line as the incident beam. Since no natural material with this specification has been discovered, in the last decade, manufactured structures with effective negative refractive index have attracted a lot of attention due to their wonderful optical properties [2,3] and imaging capabilities [4]. Such meta-materials are able to restore both the phase of propagating waves and amplitude of evanescent waves to make perfect lenses which can overcome the diffraction limit of conventional convex lenses and introduce a new class of imaging systems called “super lenses” [4].
There are several approaches to realize the negative refraction phenomena. Some meta-materials are made from arrays of metallic split-ring resonators with metallic wire strips. Negative index of refraction in these structures appears in the microwave frequency regime [5-7]. In the optical range of frequency, different designs [8] such as double-plate (or double-wire) pairs, which provide the negative magnetic permeability, and long metal wires [9], are proposed. Another human-made structure is made from arrays of lossless dielectric media named photonic crystals (PCs). These structures are able to explore the effective negative index of refraction in the infrared and optical frequencies. In contrast to the conventional lenses in which imaging effects obey the Newton’s formula, in PCs the imaging is related to mirror-inversion transformation like mirrors although PCs produce real images [10]. Furthermore, there is no need to form a curved surface to obtain an image and also we can attain sub-wavelength imaging which exceeds the diffraction limits [4].
In these regards, extensive theoretical and experimental imaging studies have been performed [11-14]. Some of the studies on negative refractive index are related to 2D triangular, hexagonal and honeycomb high symmetry lattices in the second band which can be realized as left handed behavior [15-17]. Another kind of research has concentrated on 2D square lattices in which the negative refraction effect occurs in the region of the first photonic band where an isotropic negative index cannot be defined and negative refraction can be conceived by anisotropy or higher-order Bragg scattering effects [18-20]. Focusing properties of 2D square lattice PCs in the second photonic band have been studied experimentally in the range of microwave frequencies [21]. Although negative refraction phenomena in 2D square lattices have been studied extensively, it is of significance to improve efficiency of the superlensing effect especially in near-infrared frequencies.
In this paper, for evaluation of the negative refraction effect in near-infrared frequency regime in the second photonic band of 2D square lattice PCs, where the wave has a negative phase velocity and PC structure can be assumed as a LHM, we proposed a PC comprising partitioned cylinders. We show that the image position is dependent on the source location and the slab thickness. We employ the finite difference time domain (FDTD) method with periodic boundary condition for calculating the dispersion band diagram of the PC and FDTD method incorporating the perfectly matched layer (PML) boundary condition for simulating the field pattern of the point sources and their images.
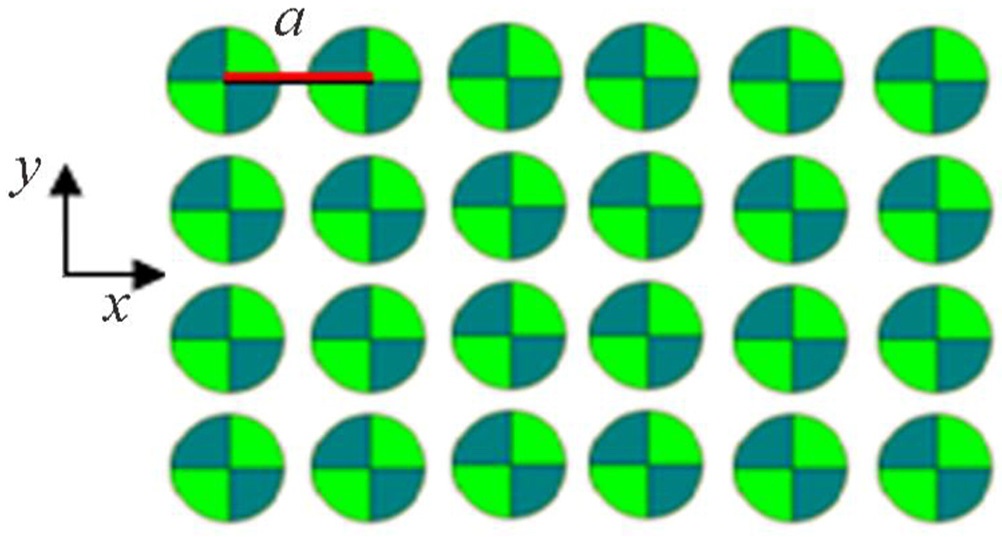
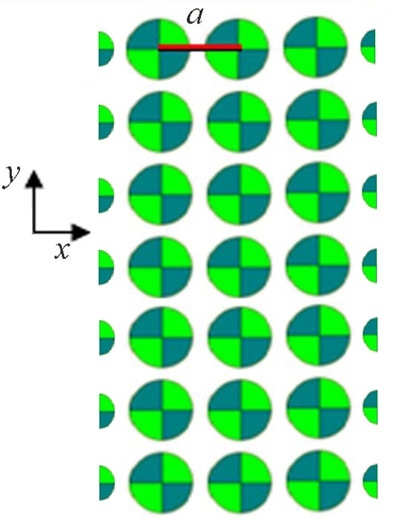
The PC proposed here is a novel 2D square lattice consisting of periodic arrays of infinitely long dielectric partitioned rods of silica and germanium in air background as depicted in Fig. 1. It is assumed that the width of the slab in the
the radius of dielectric cylinders is
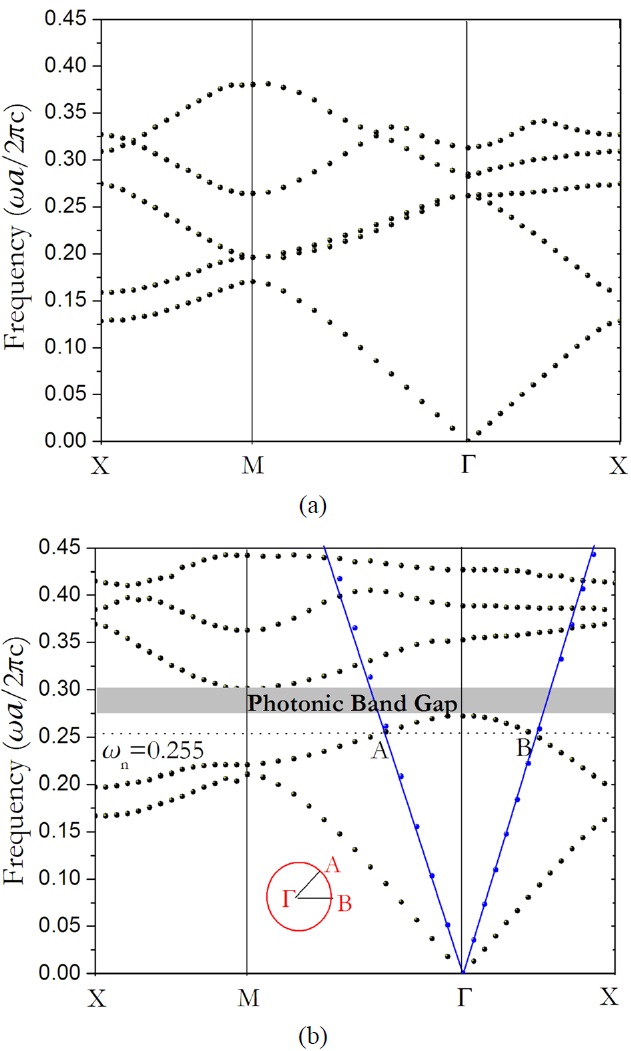
We employ the FDTD method based on Yee’s lattice to solve the Maxwell’s equations within the unit cell in the time domain by applying the periodic boundary conditions to obtain the band diagram of the PC. We identify the eigenmodes as the spectral peaks from the Fourier transform of the TM mode of the electric field in the time domain. Fig. 2 shows the calculated TM-polarized band diagram along the high-symmetry lines in the first Brillouin zone.
Fig. 2(a) displays the band diagram of common 2D square lattice PC consisting of Ge cylinders with radius of
To obtain the frequency with the negative refractive effect we should pay attention to some important conditions. First of all, the frequency should be below 0.5×2π
inset in Fig. 2(b) implies the constant frequency contour with two equal energy surfaces that is related to the second band for
III. SURFACE TERMINATION EFFECT ON IMAGE QUALITY OF THE PROPOSED STRUCTURE
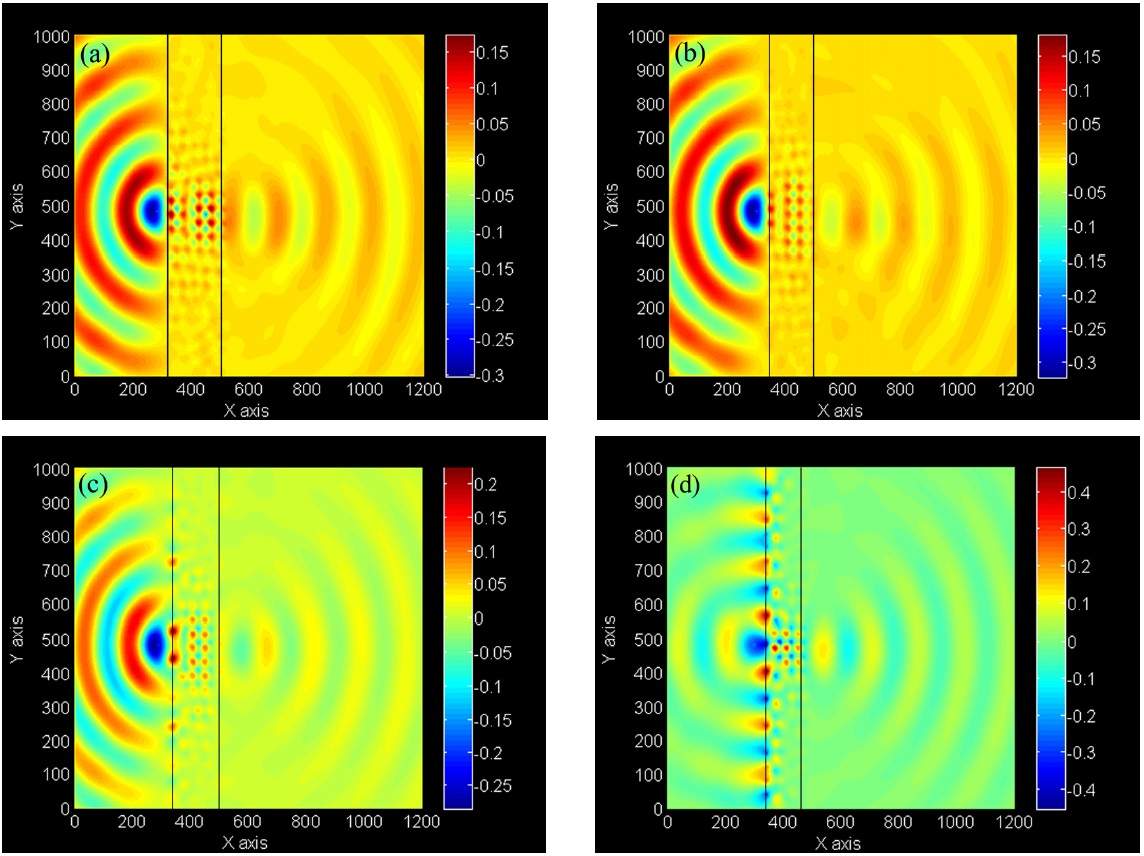
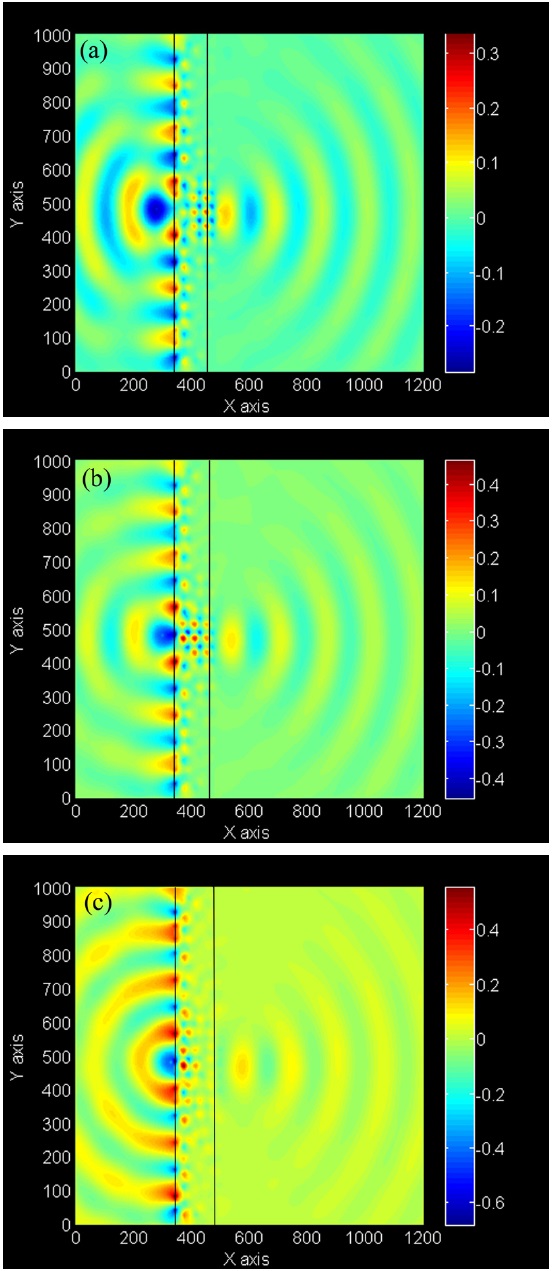
There is a type of bound photon mode in photonic crystals that is guided by the background/PC interface. This mode is the linear combination of surface states, those which are strongly affected by the position of surface termination. By coupling incident evanescent waves and bound photon modes, evanescent waves can be transmitted through the PC structure and contribute to image formation [18]. In this regard, some analysis has clarified that surface termination has a significant effect on transmission and image quality [22,23]. According to this issue, we consider a 4.9
Figure 3 shows the electric field pattern of the point source and its image when the outmost layers include (a) cylinders with radius
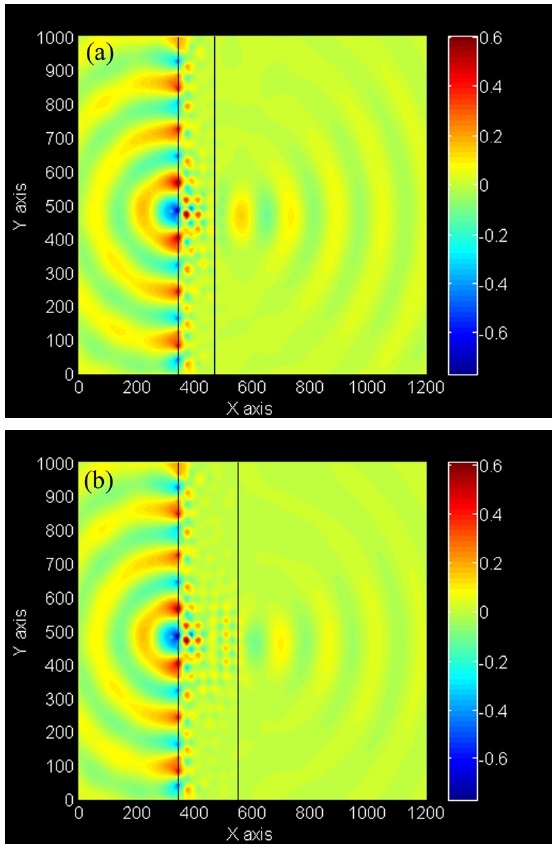
IV. IMAGE POSITION DEPENDENCY ON THE SLAB THICKNESS AND POINT SOURCE LOCATION
From the common focusing laws, one can realize whether the designed lens is able to act as a negative index material or not. A number of studies have shown that the overall imaging phenomena in PCs are defined by self-collimating and complex near-field wave scattering effects rather than negative effective index (e.g., see [24]). If the negative refraction mechanism overcomes other phenomena, by increasing the distance of point source from the slab and also by increasing
the slab thickness, image position should shift to a farther distance. Here, we consider a 4
In Fig. 7 electric field pattern of the point source located at 0.5
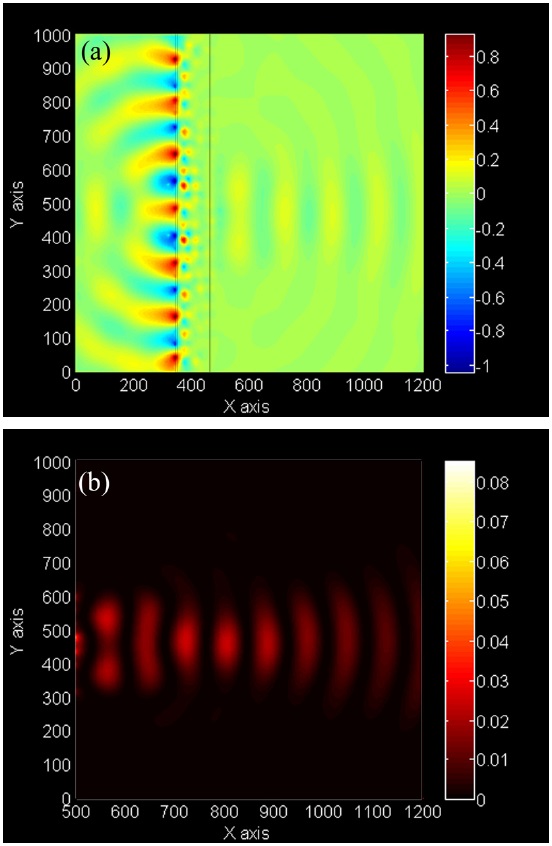
V. SUBWAVELENGTH IMAGING VIA THE DESIGNED PC LENS
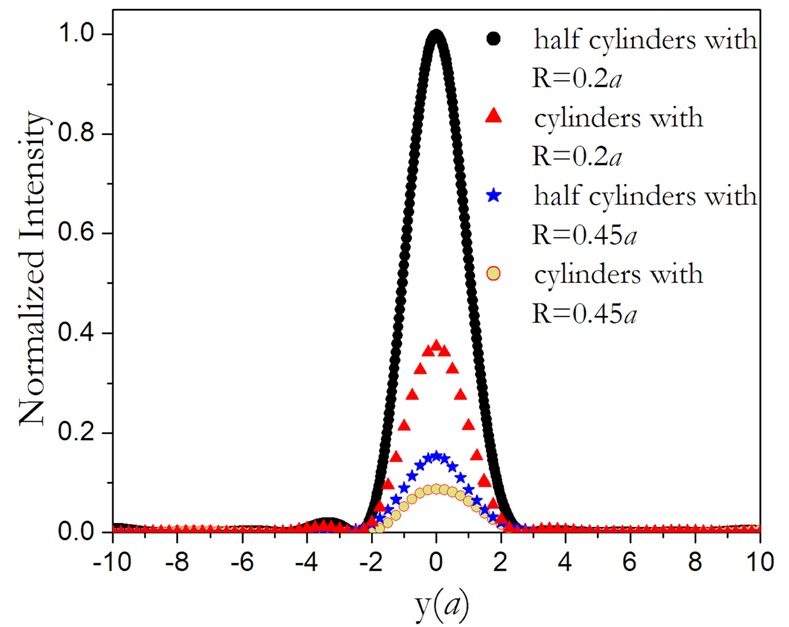
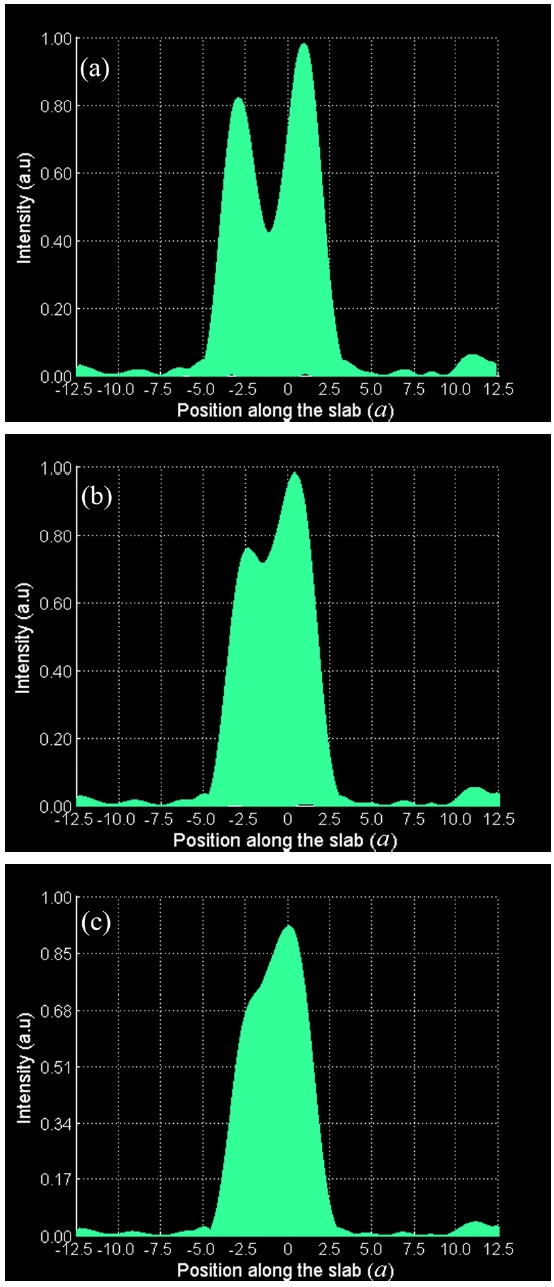
In order to study the sub-wavelength imaging and evaluate the spatial resolution of the proposed PC lens, we consider two point sources with a given vertical separation distance from each other to observe the peaks of two images clearly and then reduce this distance till the two peaks of images in the right side of the slab become obscure. For this purpose, firstly we put point sources 0.5
In this report, we introduced a 2D photonic crystal including partitioned cylinders made from Ge and SiO2 to investigate the image formation characteristics in near-infrared frequency region. We found that despite the usage of the high refractive index material Ge, the band diagram of this structure opens a gap between the second and third bands and satisfies three conditions required to create a PC lens. Although existence of sharp edges in designing such a PC structure makes some difficulties in constructing partitioned cylinders, we showed that this kind of modeling has a potential of PC superlensing in near-infrared frequency with a compressed band structure. In addition, we realized that the image formation depends on the slab thickness and the point source position from the slab. We claim that the imaging effect in our proposed partitioned cylinder PC with a properly terminated surface is dominantly governed by negative refraction effect rather than channeling or near-field scattering effects and according to Rayleigh criterion, the subwavelength focusing can occur with spatial resolution of 0.816