The finite-difference time-domain (FDTD) method is an elegant way to calculate various electromagnetic phenomena due to its strengths of easy implementation and low computational quantity [1-4]. However, the standard FDTD method (the Yee scheme [5]) has a relatively large number of numerical dispersion errors when compared to other numerical analysis methods, such as the moment method and the finite element method. Many researchers have studied low dispersion algorithms in an attempt to reduce the numerical errors of the standard FDTD method [6-13].

The higher order (2, 4) FDTD scheme (H(2, 4) scheme) is one of the low dispersion FDTD algorithms. Its weakness is that it requires a small time increment to produce accurate results, and even when a small time increment is used, its accuracy is lower than that of other low dispersion FDTD algorithms that use larger time increments at the operating frequency [11,12]. We previously presented an optimization method for the conventional H(2, 4) scheme [14]. We obtained a high level of accuracy by using the complementary dispersion properties of Yee and the H(2, 4) scheme with propagation angles, which resolved the small time increment problem of the H(2, 4) scheme. This paper expands that solution to a homogeneous, isotropic, and lossy material that has a constant conductivity for frequencies.

As in our previous study [14], this study uses a weighting factor for isotropic dispersion and two scaling factors in order to achieve an extremely small number of numerical errors. However, unlike the case in the previous study [14], we use a closed-form solution in the present study to find the weighting factor. This study found a weighting factor and two scaling factors under a square grid. Fig. 1 shows the procedure of the proposed scheme. Section Ⅱ presents the formulation of the numerical dispersion relations and the calculation of a new weighting factor by a closed-form solution. The scaling factors are calculated and the scheme’s performance is analyzed in Section Ⅲ. The numerical results of the proposed scheme and the H(2, 4) scheme are compared in Section Ⅳ.

In this section, nearly isotropic numerical phase constants for the propagation angles were obtained using a weighting factor. We assumed a square grid and found the weighting factor by using update equations and a numerical dispersion relation. The Maxwell equations used in the FDTD method are as follows:

where ？ is the electric field intensity and

is the magnetic field intensity. In addition, ε, μ, and σ are respectively the permittivity, permeability, and conductivity of a material. The following equations show the update equations of the proposed scheme at TM_z-mode. A square grid ( Δ = Δx = Δy ) is assumed.

where

is the difference operator defined as:

F_w is the weighting factor. E and H are the electric intensity and magnetic field intensity, respectively. Their subscripts indicate the field component direction. Δx and Δy denote the unit cell length of the x-direction and y-direction, respectively. Δt is a time increment. The update equations are composed of the weighting sum of the update equations of the Yee and H(2, 4) schemes. The ratio of the Yee and H(2, 4) schemes is determined by the weighting factor. If the weighting factor is one, the proposed scheme becomes the H(2, 4) scheme, and if the weighting factor is zero, the proposed scheme becomes the Yee scheme.

Eq. (8) is the numerical dispersion relation of the proposed scheme.

where

？ is the propagation angle and c is the velocity of light. As shown in Fig. 2, the numerical phase constants of the H(2, 4) scheme and the proposed scheme have similar patterns in the propagation angles. They were obtained by Newton’s method [15]. The H(2, 4) and Yee schemes have a maximum numerical phase constant on the main axes and a minimum value on the diagonal axes. However, the phase constants of the Yee scheme are larger than the analytic phase constant, while those of the H(2, 4) scheme are smaller than the analytic value. This property makes the two schemes complementary. If the proposed scheme is used, better isotropic dispersion properties will be obtained than those of the H(2, 4) scheme.

We determined the weighting factor (F_W) using the following equation:

Δβ is defined by Eq. (10) and the subscript indicates the numerical scheme (H: H(2, 4) and Y: Yee). Eq. (9) flattens the numerical wavenumbers of the proposed scheme for the propagation angles at the operating frequency.

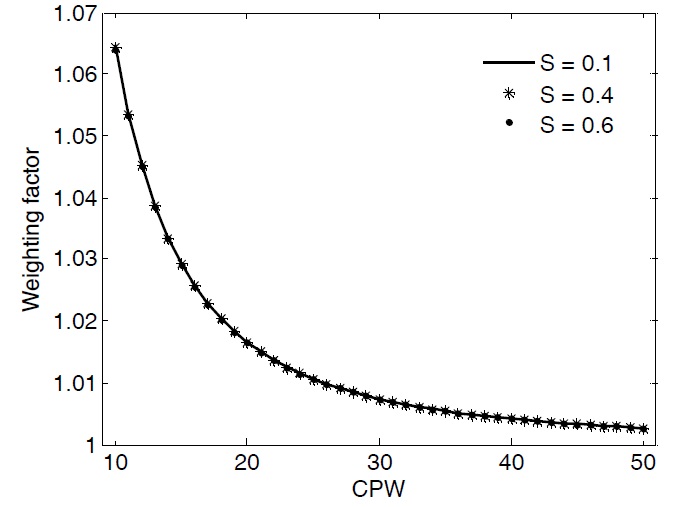
Fig. 3 shows the weighting factor versus cells per wavelength (CPW). As shown in Fig. 3, the Courant number (S) has little effect on the weighting factor. As the CPW become larger, the weighting factor approaches a value of one. Fig. 4 shows the flatness of the relative permittivity and conductivity, defined as follows:

where max(X) and min(X) stand for the maximum and minimum value of X, respectively. As shown in Fig. 4, the proposed scheme clearly has the best performance among the three schemes. Its flatness is sufficiently small to consider a constant relative permittivity and conductivity for propagation angles.

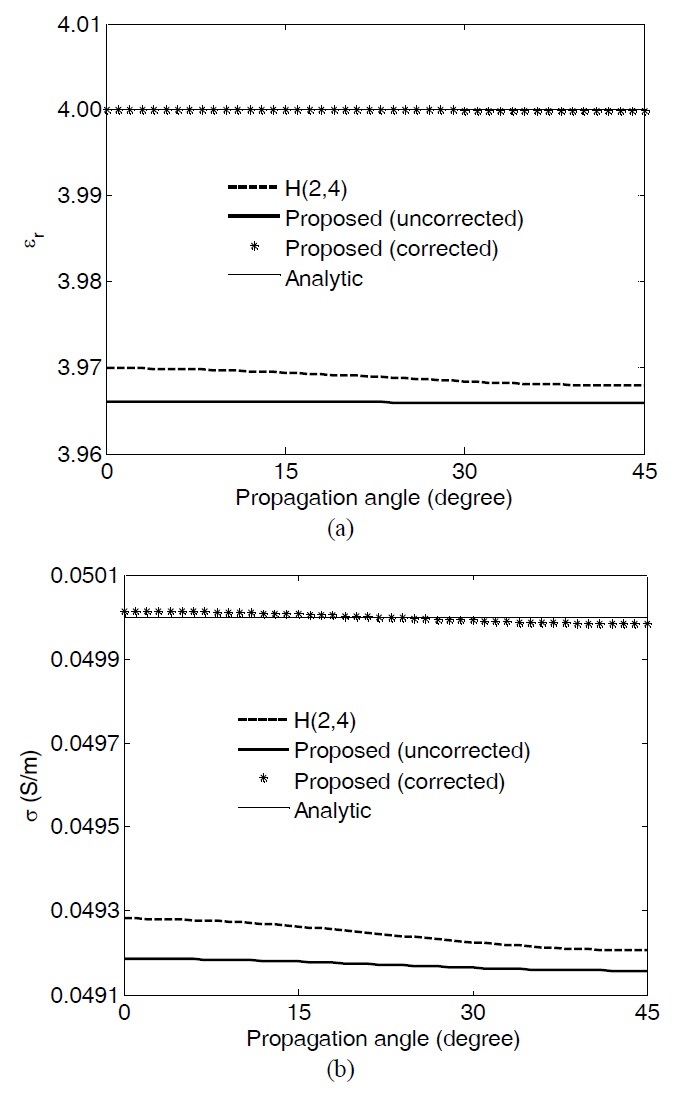
In this section, the numerical errors are removed at a single frequency. This is followed by analysis of the wide band properties. Fig. 5 shows the relative permittivity and conductivity for the propagation angles. The estimated material constants of the proposed scheme (uncorrected) are much flatter than those of the H(2, 4) scheme. However, the difference is greater between the analytic solution and these constants than between those of the H(2, 4) scheme. These numerical errors were reduced by multiplying two scaling factors, m₁ and m₂, by the relative permittivity and conductivity, respectively. These create a new relative permittivity and conductivity, defined as

These new material constants change the numerical dispersion relation. Eq. (15) represents the new numerical dispersion relation.

The numerical wavenumber

of Eq. (15) is changed into the exact wavenumber (k), thereby allowing analytical calculation of the scaling factors. The solution of Eq. (15) is derived as follows:

Re[X] and Im[X] represent the real and imaginary part of X. The corrected case in Fig. 5 then represents the final performance of the proposed scheme at the operating frequency. The estimated material constants (relative permittivity and conductivity) are almost the same as the analytic values.

The wideband properties of the proposed scheme are analyzed by defining e_ε(CPW, S) and e_σ(CPW, S) as follows:

where

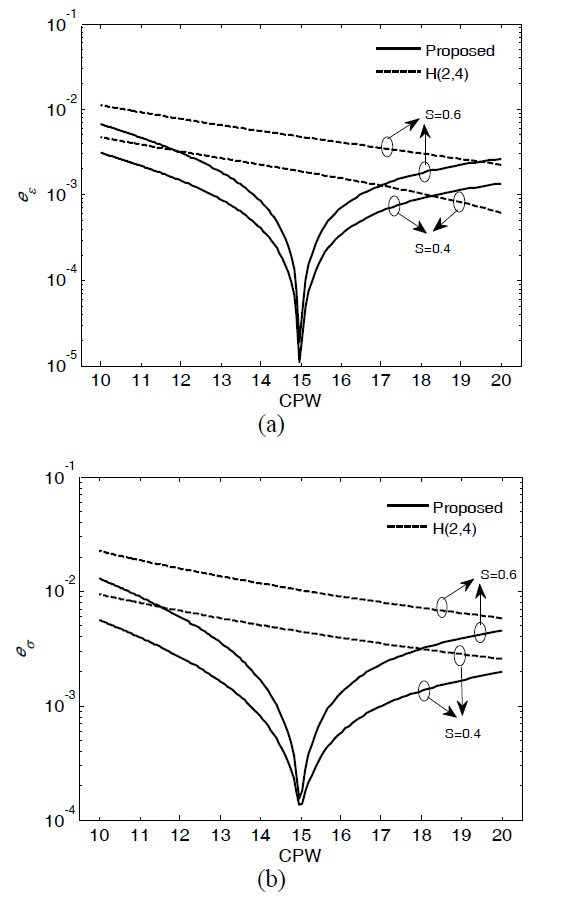
are the estimated relative permittivity and conductivity, respectively. Fig. 6 the proposed scheme has a much better performance than the H(2, 4) scheme for the wide CPW region. As expected,sed scheme has an extremely small error in the selected CPW. In addition,sed scheme has similar accuracy for the different Courant numbers in the selected CPW.

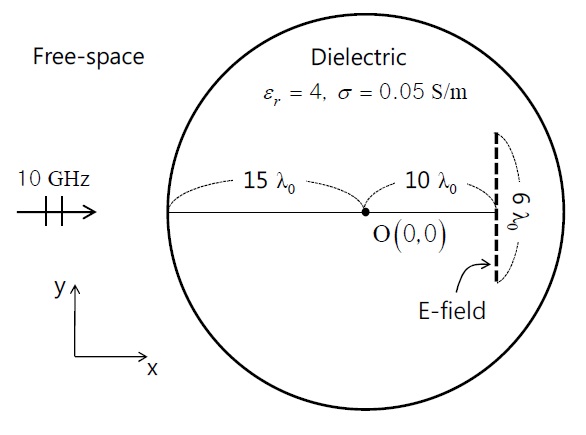
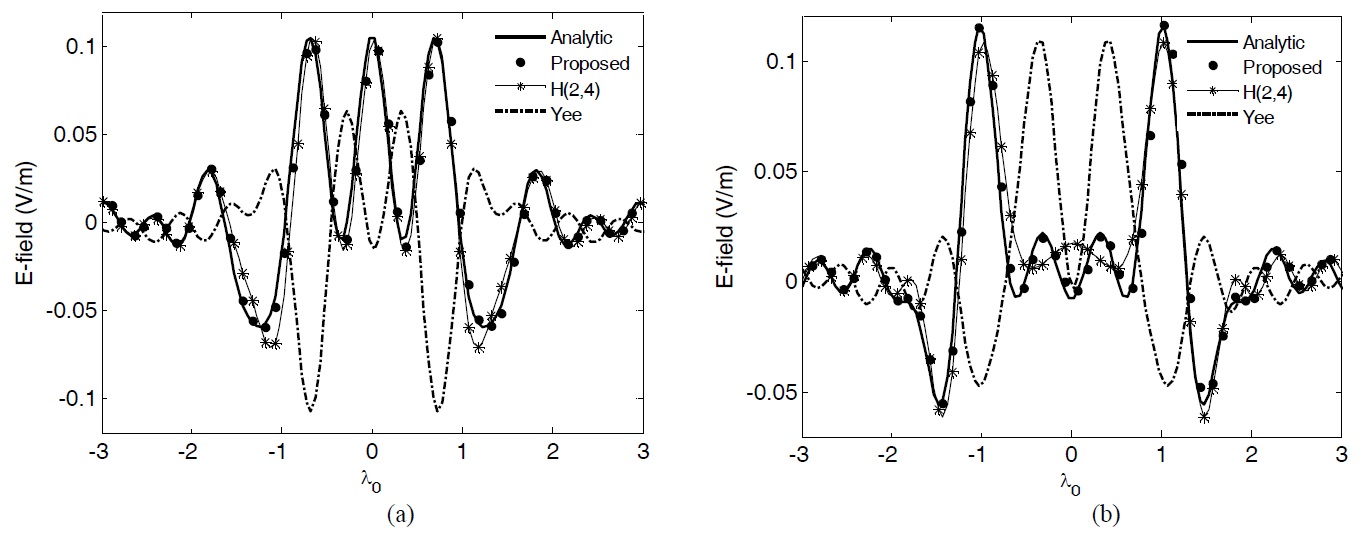
The validity of the proposed scheme for lossy material was verified by calculating a scattering problem of the lossy circular dielectric. The radius of the dielectric is 15 λ₀ at 10 GHz. The dielectric is ε_r =44 and σ = 0.05 S/m. A single tone plane wave is used as a source. Fig. 7 shows the simulation structure and conditions. The simulation settings are 20 CPW and 0.6 S at 10 GHz. The weighting factor and scaling factors are calculated by Eqs. (9), (16), and (17). The exact solutions were found in [8] and are compared with the calculated results. Fig. 8 shows that the results of the proposed scheme are in better agreement with the analytic solutions than are the results of the H(2, 4) and Yee schemes.

In this study, we expanded the optimized H(2, 4) scheme to a lossy material and assumed a square grid. A weighting factor calculated by a closed-form solution was used to obtain isotropic dispersion in the proposed scheme. Two scaling factors were applied to the relative permittivity and conductivity and removed the numerical errors in the optimized CPW. The proposed scheme has better performance than the H(2, 4) scheme with the optimized CPW. The proposed scheme can be used effectively in electrically large problems, and can easily be expanded to 3D.