



Recently, a strong trend in communication has been to include multimedia contents such as video, images, voice, music, text, etc., rather than just a single form of media. Image and/or video contents are especially preferred because of their very information-rich properties. However, their large quantity of data requires a wide communication bandwidth. Thus, for the last few decades, most research and development in this area has been on the reduction of the amount of data they contain [1-3].
A digital hologram is a technique in which the interference patterns between the reference light wave and the object light wave are captured with a charge-coupled device (CCD) camera or calculated from an algorithm on a computer (computer-generated hologram, CGH) [4,5] instead of writing it on holographic film [6]. The original image can be reconstructed by loading the digital hologram on a spatial light modulator and illuminating the reference light, which is the same as was recorded. A hologram is a relatively expensive form of 3-dimensional (3D) image content, and recently researchers at many institutions around the world have been studying encryption techniques for holograms. However, most of them are optical methods that use optical elements or optical parameters to hide information [7].
In this paper, we try to encrypt a digital hologram electronically, not optically. This includes both spatialdomain encryption and frequency-domain encryption. For the frequency domain, both the discrete Fresnel transform (DFT) and discrete cosine transform (DCT) are considered as the transform methodologies from spatial-domain data to frequency-domain data. In each domain, we try to find the best encryption method. Therefore, the main purpose of this paper is to examine the possibility of electronic encryption of a digital hologram. For the digital hologram, we use the digital holograms created by means of the CGH technique.
II. PROPOSED SCRAMBLING METHODS
In this section, we try several attempts to hide the contents of a digital hologram in both the spatial domain and frequency domain. In the frequency domain, we consider both the global DCT (GDCT) domain and DFT domain.
>
A. Scrambling in the Spatial Domain
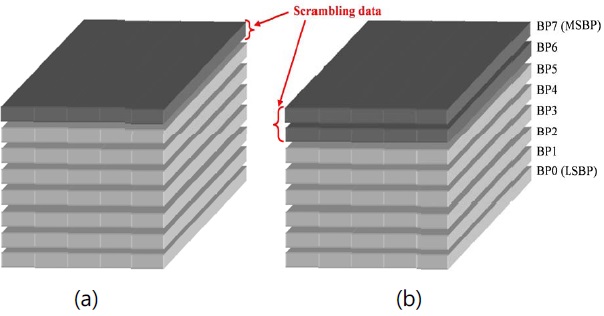
In the spatial domain, it is not easy to determine which coefficients in digital holograms are important in reconstructing the holographic object. Thus, we focused our attention on the bit-planes (BPs) of the whole or a segment of the digital hologram. However, as explained above, because a segment of a digital hologram can be used to reconstruct the image, it is useless to hide a part or a segment of a digital hologram. Thus, to encrypt in the spatial domain, the whole digital hologram should be considered. Note that each BP has the same amount of data, even though the importance level of each BP is different.
Fig. 1 shows the scrambling schemes in the spatial domain. As shown in Section II, BP7 is the most important one (most significant bit-plane, MSBP). Thus, the first consideration is to encrypt the BP7, as in Fig. 1(a). In Fig. 2, an example of the resultant reconstructed image from the spatial-domain scrambling. Fig. 2(c) is the result by scrambling only BP7 of the digital hologram in Fig. 2(b). When it is compared to the original image of Fig. 2(a), it is clear that the information is still configurable. Thus, we added BP6 to the data to be scrambled following the scheme shown in Fig. 1(b).
Fig. 2(d) is the example of the resulting reconstructed image by this scheme, whose content is totally unrecognizable. For each of the digital holograms considered, scrambling BP7 and BP6 was enough to hide the contents of the 3D image.
Note that BP7 and BP6 are one-fourth of the amount of data of the original digital hologram. That means that at least one-fourth of the digital hologram should be scrambled to hide the information of the 3D image. If we assume that a digital hologram has the size of 1,024×1,024, more than 2 Mbits (2,097,152 bits) need to be encrypted. As will be shown in the following, this amount of data is relatively high compared to that of the frequency domain scheme
>
B. Scrambling in Frequency Domain
For the frequency domain, we considered both the global DCT and Fresnel transform.
1) Scrambling in the DCT Domain
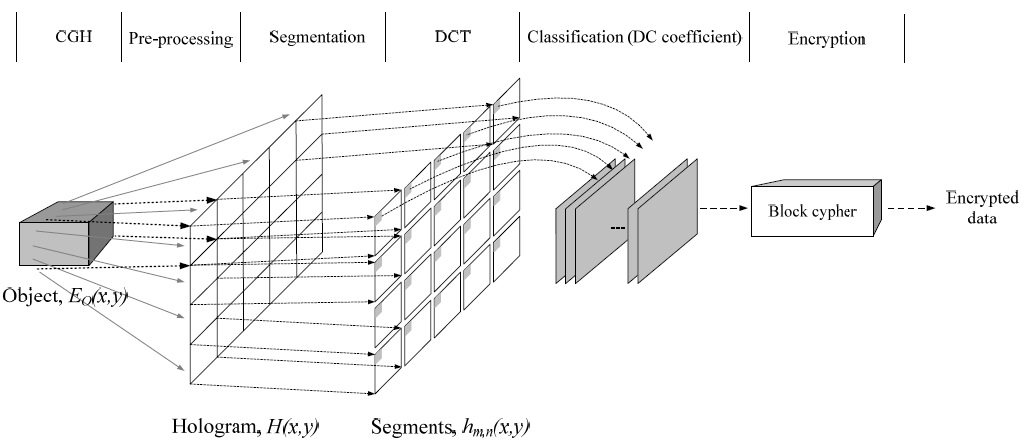
As mentioned before, the DCT is performed by the unit of a given size of coefficient block. Thus, there can be two kinds of scrambling methods for GDCT domain data. The first one is to select the appropriate number of DCT coefficients after the DCT for the whole digital hologram. Of course, the coefficients should be the ones retaining as much energy as possible. The second method is that after appropriate segmentation of the digital hologram and performing DCT for each segment, only a few coefficients
(say, only the DC coefficients in the extreme) from each segment are taken to be scrambled. The first method has the problem that it is not easy to find the coefficients retaining the highest energies in general. Therefore, we decided to choose the second method. For the coefficients also, we decided to take only the DC coefficients because it is the most promising way to hide the highest energy.
In this methodology (Fig. 3), after segmentation and DCT, only DC coefficients are taken to form a scrambling block (128 bits in this paper). Each scrambling block is scrambled separately with a block cipher method (Advanced Encryption Standard [AES]-128 in this paper). Each of the resulting bits is relocated to its original place. Then, the result is inverse-DCTed and reconstructed to form the corresponding 3D image.
Fig. 4 shows several examples of the reconstructed images after scrambling for various segment sizes. Note that the number of coefficients to be scrambled is the same as the number of segments. As can see in the figures, all the cases considered showed satisfied scrambling results. However, in the case of segmentation to 256×256 segments, the original image is a still a bit recognizable if it is enlarged in some of the test images. Thus, the safe approach is to segment a digital hologram into 128×128 blocks. In this case, only 512 bits need to be scrambled if a DCT coefficient consists of 8 bits. Compared to the spatial-domain scrambling case, DCT-domain scrambling is much more effective, specifically, 4,096 times more effective.
2) Scrambling in Fresnel Domain
This encryption algorithm is based on a Fresnel transform. For encryption, the Fresnel transform is performed by regarding a digital hologram as a natural 2D image.
If we analyze the results of previous study [7] shown with regard to the properties of sampling, localization, and transformation, we can obtain two characteristics.
The first is that a local region of a digital hologram contains information about the entire object. Second is that it has a frequency characteristic that is different from natural images. From such characteristics, the following conclusions can be made. Because the local region of a digital hologram includes information for the entire object, we must encrypt the entire hologram rather than a segment of the hologram.
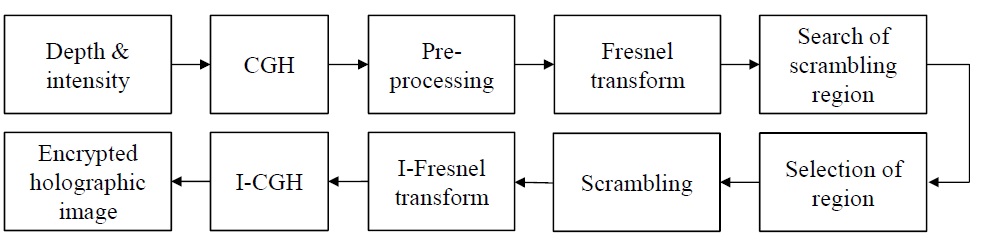
Fig. 5 shows the scrambling schemes in the Fresnel domain. The encryption methodology is the following:
1) Fresnel transform
2) Selection of encrypted region
3) Encryption using block cipher
4) Inverse Fresnel transform
[Fig. 5.] Methodology and procedure for Fresnel-domain scrambling. CGH: computer-generated hologram.
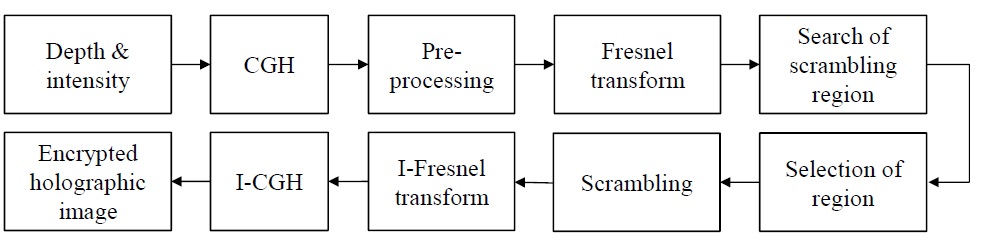
Fig. 6 shows a Fresnel transform result image. As shown in Fig. 6, the result from DFT of a digital hologram shows a similar image to the original one in the right bottom part. Using this characteristic, this paper proposes a scrambling scheme in the DFT domain.
To apply the proposed algorithm, digital holograms of 3D objects (depth map, intensity) are generated using the CGH method. The proposed algorithm is applied to them. The encryption results are verified numerically using the peak noise-to-signal ratio and normalized correlation. In addition to the numerical statistics, visual observation is used to determine the encryption efficiency. The size of a digital hologram is 1,024×1,024 pixels.
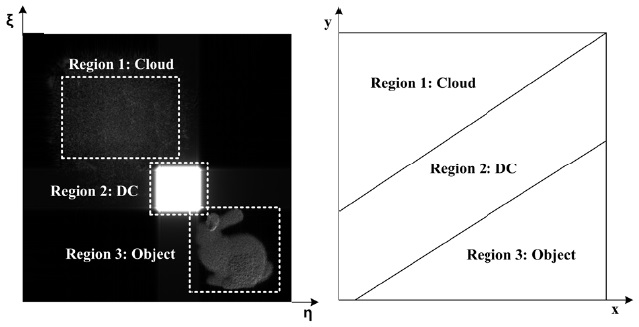
We divided the digital hologram into three regions in the DFT domain, whose scheme is shown in Fig. 7. Here, we are scrambling the “object” region. The scrambling results are shown in Fig. 7 for all of the three regions. As can be seen from the figure, the scrambling effect is highest in the “Object” region. Fig. 8 shows several examples of the reconstructed images after scrambling for the three regions.
This paper introduced several methods for scrambling a digital hologram in the frequency domain as well as the spatial domain. For the frequency domain, both 2DDCT and 2DDFT were considered. The purpose of this study was to find a scrambling method with the highest efficiency and lowest cost with the requirement of hiding the image information unrecognizably. The reason for considering the frequency domain is that a transform to the frequency domain concentrates the energy of the image to a certain frequency band(s), and it is more efficient to disturb the information in the higher energy coefficients.
Consequently, the GDCT/DFT-domain scrambling schemes can be used efficiently to encrypt the digital hologram. The frequency-domain schemes are especially suitable when used during the data compression process (on-site scrambling), which includes the DFT-domain scheme.

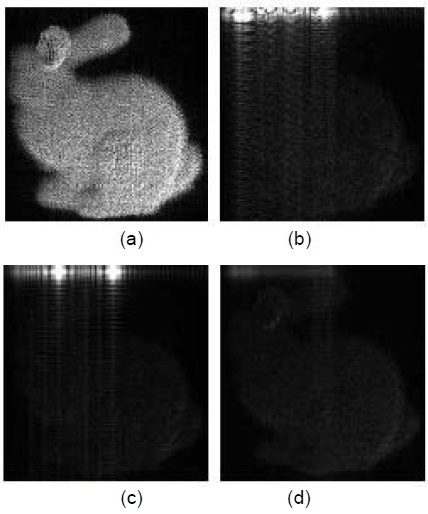

![Data-scrambling results: (a) original holographic reconstruction object, (b) “Cloud” region scrambling (peak noise-to-signal ratio [PSNR], 15.68 dB), (c) “DC” region scrambling (PSNR, 16.42 dB), and (d) “Object” region scrambling (PSNR, 15.80 dB).](http://oak.go.kr/repository/journal/12434/E1ICAW_2013_v11n3_185_f008.jpg)