High-electron-mobility transistors (HEMTs) have been highlighted as essential high-frequency devices for various state-of-the-art microwave or millimeter-wave application systems, such as satellite communication, electronic warfare, radiometry, base stations, and smart weapons [1-3]. These systems require not only excellent radio frequency (RF) characteristics but also high-power performances for their specific applications [4]. The enhancement of power characteristics can be achieved by improving the current level or breakdown voltage of the HEMTs. A variety of methods have been used to increase the power performance of HEMTs these include the GaN/AlGaN material system [5,6], the gate-fieldplate technique [7,8], and the adoption of composite channel systems [9,10]. Most of these methods have focused on the enhancement of transistor power by increasing the breakdown voltage. These technologies, however, have some drawbacks, such as high cost and difficulty in material growth of the composite channel HEMTs, poor RF characteristics of the GaN HEMTs, and low electron mobility and large increase in the parasitic capacitances of the gate-field-plated HEMTs. As a consequence, in many application achieving a large current level by simply increasing the transistor gate_width (w) has been one of the most economic and practical methods in terms of circuit design and device fabrication.

A very long gate width or multi-finger gates are effective, but an increase in w gives rise to a large gate resistance (R_g), thereby causing degradation of noise characteristics [11] and the maximum frequency of oscillation (f_max) [12]. Therefore, it preferable to achieve a long effective gate width with no significant increase or even reduction in R_g. The use of a wide-head T-gate was reported [11] as an exemplary method for suppressing R_g; however, this technique has a limit in expanding the gate head because high source-to-drain channel resistance is unavoidable under increased source-drain spacing for accommodating a wide gate-head dimension; consequently, the structural instability of the T-gate increases in this structure. Even though studies [13-15] have documented the critical role of R_g in the high-frequency characteristics of HEMTs based on a small-signal- equivalent circuit model, there has been minimal investigation in reducing R_g in HEMTs with long gate_ widths or multi-finger gates. In this study, we investigated the multi-finger structures of the HEMTs affecting R_g and high-frequency characteristics. Because R_g is strongly influenced by a number of gate_fingers (N) and gate_widths (w) of the device structure, we examined the effects of all these parameters on R_g and the device characteristics by using various combinations of structural parameters for the 0.1-μm depletion-mode InGa- As/InAlAs metamorphic HEMT (MHEMT). To investigate the effects of N and w, 12 different gate peripheries were fabricated with various gate fingers (2, 4, and 6) and gate widths (25, 40, 50, and 70 μm). Except for the variations in N and w, we maintained the same epitaxial structure, gate length of 0.1-μm, and source-drain spacing of 2-μm for all fabricated devices, as described in the next section.

The MHEMT micrograph of the HEMT with four fingers is shown in Fig. 1.

As shown in Fig. 2, the MHEMT epitaxial structure was grown by molecular beam epitaxy on a semi-insulating GaAs substrate. The structures consisted of the following layers from the bottom: a 1000-nm In_xAl_1-xAs linearly graded buffer layer with an indium mole fraction, x, linearly graded from 0 to 0.5; a 300-nm undoped In_0.52Al_0.48As buffer layer; a silicon delta-doped plane (1.3×10¹²/cm²), a 4-nm undoped In_0.52Al_0.48As spacer layer; a 23-nm undoped In_0.53Ga_0.47As channel layer; a 3-nm undoped In_0.52Al_0.48As spacer layer; a silicon delta- doped plane (4.5×10¹²/cm²); a 15-nm undoped In_0.52 Al_0.48As Schottky barrier layer; and a 15-nm n-type In_0.53Ga_0.47As cap layer (6×10¹⁸/cm³). The grown epitaxial layer showed a two-dimensional electron carrier density (n_s) of about 3.5×10¹²/cm² and a Hall mobility of about 9,700 cm²/Vsec at room temperature.

To fabricate the MHEMTs, we first isolated active areas by using mesa etching with an etchant of phosphoric acid/H₂O₂/H₂O (1:1:60) to reduce the thickness to 200-nm. AuGe/Ni/Au (140/30/160 nm) ohmic metallization showed a specific contact resistance of about 5×10^―7 Ω-cm² after rapid thermal annealing at 320℃ for 60 seconds in a vacuum. An electron beam lithography system (EBPG-4HR, Leica Microsystems Ltd., Buffalo Grove, IL, USA) was used to perform 0.1-μm T-shaped gate patterning upon completion gate_recess, gate metallization was performed by evaporating Ti/Au (50/400 nm) followed by metal lift-off. The MHEMTs were passivated with the Si₃N₄ films (80 nm). Finally, a Ti/Au (30/700 nm) air-bridge interconnection was made to connect the source pad.

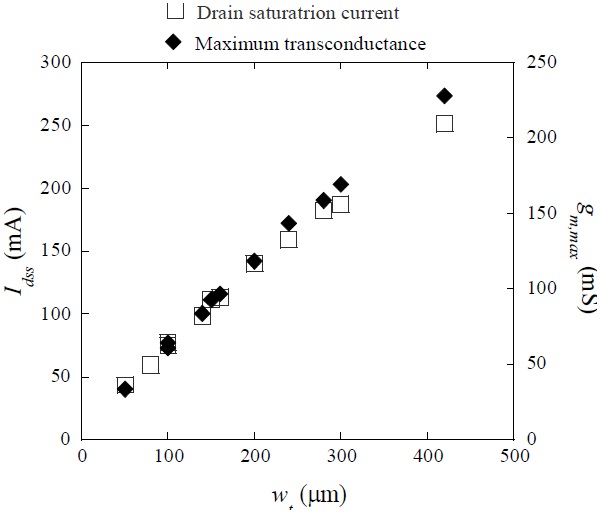
The DC characteristics of each MHEMT were measured in an HP 4156 DC parameter analyzer. Drain current (I_ds) versus gate voltage (V_gs) and transfer characteristics of the MHEMTs (at a drain voltage [V_ds] of 1.2 V) were measured at various N and w values. With the total gate width (w_t), the saturation drain current (I_dss) and maximum transconductance (g_m,max) were linearly increased at constant slopes of about 0.58 mA/μm and 0.57 mS/μm, respectively, as shown in Fig. 3. The w_t is hereafter defined as “total gate width” and given by the product of N and w. The scaling rules for these parameters are then simply expressed as:

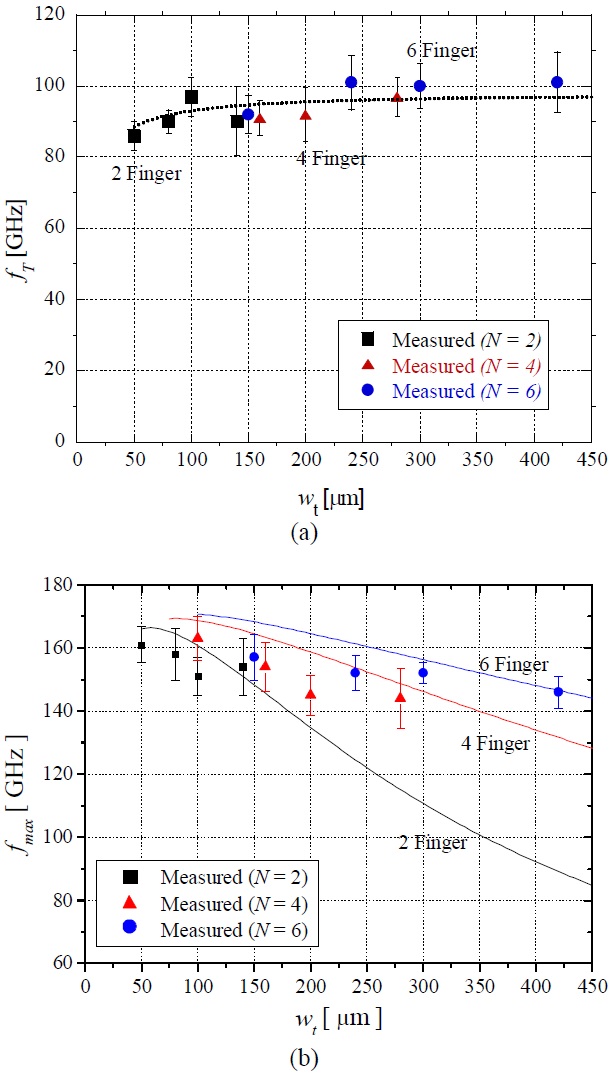
High-frequency characteristics of the fabricated MHEMTs were measured in the frequency range of 0.5 to 50 GHz using an HP8510C network parameter analyzer (Agilent Technologies, Palo Alto, CA, USA). Cut-off frequency (f_T ) and f_max were determined by extrapolating the h₂₁ and U gain curves, respectively, at a slope of 6 dB/octave. The DC and RF data were measured from each gate type of the MHEMTs at six different dies a 2.5×2.5 cm² specimen. The average f_T and f_max from the MHEMTs with 12 different gate types measured from six different dies were plotted respectively in Fig. 4 with their standard deviations (1σ). The f_T increased slightly in a small w_t region and was saturated to a frequency of about 100 GHz; on the other hand, the f_max decreased continuously with the w_t in our whole experimental range of w_t, and the reduction ratio was a function of N.

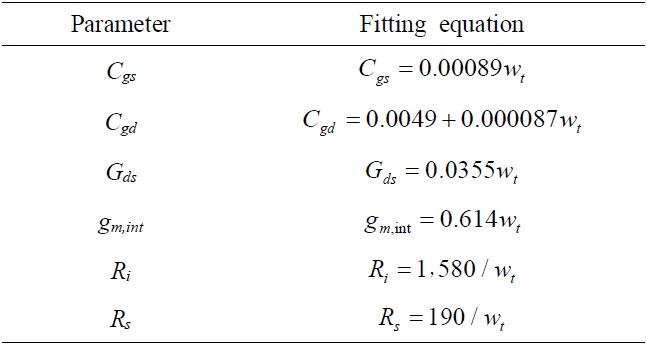
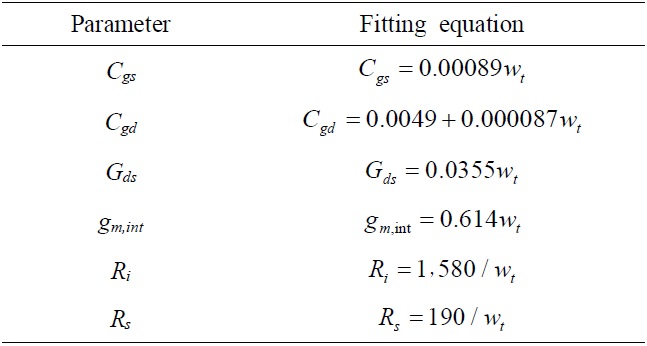
To examine the effects of N and w_t on the small-signal parameters directly affecting f_T and f_max, all the parameters shown in Eqs. (2) and (3) [16,17] were extracted from the fabricated MHEMTs by the Dambrine method [18] and curve-fitted to simple functions of w_t. As shown in Table 1, gate-to-source capacitance (C_gs), gate-to-drain capacitance (C_gd), drain conductance (G_ds), and intrinsic transconductance (g_m,int) were proportional to w_t.

However, intrinsic resistance (R_i) and source resistance (R_s) were inversely proportional to w_t. All these parameters were functions of w_t. But were not functions of N; however, one exception was R_g, which was a function of both w_t and N.

The relationships of the fitted parameters with w_t can be explained as follows. C_gs is a function of C_gso which is gate-to-source capacitance per unit gate width, and therefore is expressed as

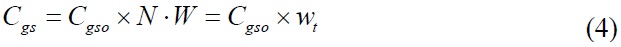
where C_gso is about 0.00089 pF/μm in our case. In the case of the C_gd, y-axis intercepts should also be considered. A non-zero C_gd at zero w_t can be formed between the gate bus line and drain pad and this parasitic capacitance, in fact, has been observed in earlier studies [13,19,20]. In our case, the y-axis intercept of C_gd was about 0.0049 pF, and the proportionality constant was about 0.000087 pF/μm. The linear relationship of G_ds with w_t can be understood such that the total sourcedrain conductance is given by (dI_ds/dV_ds per unit gate width)×w_t, and the corresponding proportionality constant was about 0.0355 mS/μm in our case. R_s and R_i were inversely proportional to w_t and curve-fitted in the same way with the proportionality constants of about 190 and about 1,580 Ω？μm, respectively. The linear increase of g_m,int with w_t can be explained by the linear scaling rule of g_m,ext with w_t, as shown in Eq. (1); the proportionality constant was about 0.614 mS/μm.

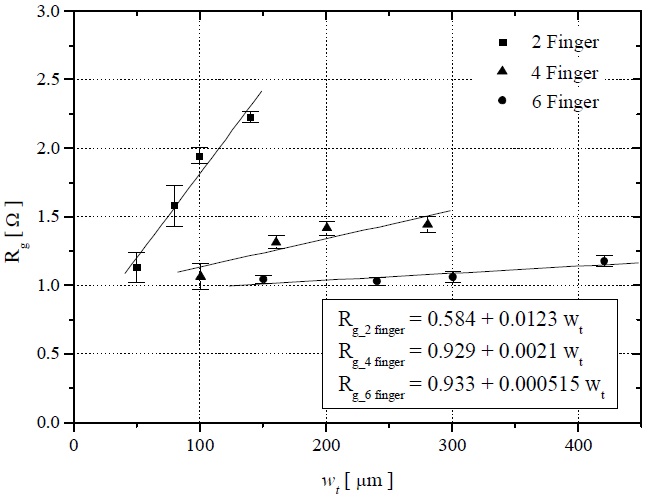
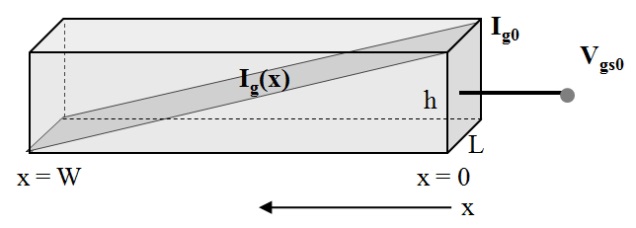
R_g is a function of both N and w_t, as shown in Fig. 5, and can be expressed as Eq. (5) where ρ_G is the resistivity of the gate metal, and A is the cross-sectional area of the gate. R_o is the y-axis intercept obtained by linear curve fitting. This relationship can be obtained by assuming the gradual (linear) reduction in gate current (I_g) density as the open end is approached, as illustrated in Fig. 6, and an essentially uniform displacement current fed from the bottom of the gate to the channel region of the HEMTs [21]. In the open-ended gate structure shown in Fig. 6, I_g and the infinitesimal change of V_gs (δV_gs) over δx are given by Eqs. (6) and (7),

where L and h are gate-length and gate-height, respectively. The minus sign in Eq. (7) indicates that gate voltage decreases with increasing x. At x=0, V_gs is equal to V_gs0, gate terminal voltage. Gate voltage V_gs (x) is obtained by integrating Eq. (7) with the boundary condition at x=0.

The average gate voltage is equal to the integral of V_gs (x) from x=0 to W and then divided by W. After carrying out the definition, we find the average value to be

The average intrinsic gate resistance inside the gate electrode region from x=0 to w is then given by:

Investigations have focused on R_o, R_g when w approaches zero [21,22]; however, the model for R_o, is still not fully understood. In our case, the y-axis intercepts of the MHEMTs (N=2, 4, and 6) range from about 0.6 to 0.9 Ω, with the corresponding proportionality constants of about 0.0123, 0.0021, and 0.000515 Ω/μm, respectively, as shown in Fig. 4. Therefore, the scaling rules of the small-signal parameters can be summarized as follows:

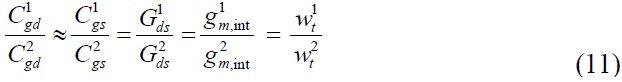
f_T and f_max can be calculated by substituting each small-signal parameter of Eqs. (2) and (3) with the curve-fitting equations in Table 1. The calculated results are plotted in Fig. 4 with measurements at each N and w_t. Good agreement was obtained from the calculated f_T and f_max with the measured data over the entire range of measured w_t. Some discrepancies between the measurements and the calculations are due to the errors associated with the device process in pattern lithography. Because g_m and C_gs are both proportional to w_t, as shown in Eq. (2), f_T is not a function of w_t. From our calculations contained in Fig. 3, f_T showed an almost constant frequency of about 100 GHz above a w_t of about 100-μm. Below this w_t f_T a slight increase with w_t owing to the y-axis intercept effect of C_gd, as observed in many earlier studies [23,24]. Since f_max is a strong function of R_g as shown in Eq. (3), it is affected by both N and w_t. If we assume that G_ds is negligible (ideal case without channel length modulation), Eq. (3) is simply expressed as [25]:

Because f_T is almost constant, we therefore obtain:

Eq. (15) shows that a careful combination of N and w_t is required to achieve a maximum f_max in a given device technology. Obviously, a greater w_t produces a higher f_max; however, to increase the number of gate-fingers by reducing the unit gate width is more efficient than to simply increase the single-gate_width in order to maximize f_max at a given w_t.

We investigated the effects of N and w on the RF characteristics of 0.1-μm depletion-mode multi-finger MHEMTs and their small-signal parameters. C_gs, C_gd, G_ds, and g_m,int were all proportional to w_t; however, R_i and R_s were inversely proportional to w_t. R_g was proportional to both w_t and 1/N². f_T and f_max were calculated by using the small-signal models and curve-fitting equations from each extracted small-signal parameters. The calculations showed good agreements with the measurements, and the results demonstrated that a greater w_t produces a higher f_max; however, to maximize f_max at a given w_t, increasing the number of gate_fingers is more efficient than increasing the single-gate width. On the other hand, f_T showed an almost independent relationship with w_t. To our knowledge, this is the first successful demonstration of multi-finger gate-width scaling effects (individual effect of N and w_t) on HEMT devices operating at millimeter-wave frequencies.