Recently, a large class of financial engineering problems dealing with index tracking and portfolio optimization have been considered as an important application domain for several types of engineering and applied mathematics principles [1-8]. Because this class can be conveniently viewed and formulated as an optimal decision-making problem in a highly uncertain and stochastic environment, particularly pertinent to this problem are approaches based on stochastic optimal control methods. The stock index tracking problem is concerned with constructing a stock portfolio that mimics or closely tracks the returns of a stock index such as the S&P 500. Stock index tracking is of practical importance since it is one of the important methods used in a passive approach to equity portfolio management and to index fund management. To minimize tracking error against the target index, usually full replication, in which the stocks are held according to their own weights in the index, or quasi-full replication is adopted by the fund managers. An exchange traded fund (ETF) is a good example of such portfolio management since it is constructed according to its own portfolio deposit file (PDF). Such a full replication or quasi-full replication can be very costly owing to transaction and fund administration costs. The constrained index tracking considered in this paper is concerned with tracking a stock index by investing in only a subset of the stocks in the target index under some constraints. Because it uses only a subset of the stocks and is expected to dramatically reduce the management costs involved in index tracking and simplify portfolio rebalancing more effectively, this problem is particularly important to portfolio managers [7]. Successfully constrained index tracking is also expected to increase the liquidity of an ETF since we may be able to construct the same ETF without investing in the same quantity of stocks in its PDF. To achieve good tracking performance with a subset of stocks in the index, several methods (e.g., control theory [1,4], use of genetic algorithms [3], and evolutionary methods [2]) have been studied by researchers.

In this paper, we consider the use of approximate dynamic programming (ADP) for solving the constrained index tracking problem. Recently, the use of ADP methods has become popular in the area of stochastic control [9-12]. As is well known, solutions to optimally controlled stochastic systems can be well explained by using dynamic programming (DP) [9,10]. However, stochastic control problems cannot be solved by DP exactly except in very simple cases, and to obtain good suboptimal policies, many studies rely on ADP methods. ADP methods have been successfully applied to many real-world problems [13], including some financial engineering problems such as portfolio optimization [5,11,12]. The main objective of this paper is to extend the use of ADP to the field of index tracking. More specifically, we (slightly) modify a mathematical formulation of the constrained index tracking problem in [1,4] and establish an ADP-based procedure for solving the resultant stochastic state-space control formulation. Simulation results show that this procedure works well when applied to real financial market data.

The remainder of this paper is organized as follows: In Section 2, preliminaries are provided regarding constrained index tracking and ADP. In Section 3, we describe our main results from an ADP-based control procedure for the constrained index tracking problem. In Section 4, the effectiveness of the ADPbased procedure is illustrated by using real financial market data. Finally, in Section 5, concluding remarks are presented.

In this paper, we examine constrained index tracking based on ADP. In the following, we describe some fundamentals regarding constrained index tracking and ADP.

In this section, we describe a constrained index tracking problem [1,4], in which an index of stocks is tracked with a subset of these stocks under certain constraints, as a stochastic control problem. We consider the index I(t) defined as a weighted average of n stock prices, s₁(t), · · · , s_n(t). Note that the stock prices are generally modeled as correlated geometric Brownian motions [1,14], i.e.,

where

is the drift of the ith stock, and

is a vector Brownian motion satisfying

By performing discretization using the Euler method with time step Δt, one can transform Eq. (1) into the following discretetime asset dynamics [14]:

where

Note that with

we have

Further, note that with

the index value defined by a weighted average can be expressed as

for some α ∈ Rⁿ satisfying α_i ≥ 0, ∀i ∈ {1,· · · , n}, and

Without loss of generality, in this paper we assume

i.e., the index I(t) is assumed to be the equally weighted average of the stock prices. Under this assumption, we have

Extending the results of this paper to a general α case will be straightforward. The continuous dynamics for the risk-free asset (e.g., the continuous time bond) can be modeled by

where

is the risk-free rate [14]. When the time step is Δt, its discretized version can be written as

where

[14]. We assume that the money amounts of the first m < n stocks, y₁(t), · · · , y_m(t), and the amount of the risk-free asset, y_C(t), consist of our portfolio vector y(t) at time t, i.e.,

Note that it is the total value of this portfolio vector that should track the index value over time. More precisely, our goal is to let the wealth of our portfolio,

approach sufficiently close to the index value I(t) = α^Ts(t) as t → ∞ by performing appropriate trades, U₁(t), · · · u_m(t) and u_C(t) for the first m stocks and the risk-free asset, respectively, at the beginning of each time step t. Hence, a solution to the constrained index tracking problem can be found by considering the following optimization problem:

where γ (0, 1) is a discount factor, dist(a, b) is the distance between a and b, and C_t is a constraint set. Details about the distance function, dist(a, b), and the constraint set, C_t, are presented in Section 3.

Dynamic programming (DP) is a branch of control theory concerned with finding the optimal control policy that can minimize costs in interactions with an environment. DP is one of the most important theoretical tools in the study of stochastic control. A variety of topics on DP and stochastic control have been well addressed in [9-12]. In the following, some fundamental concepts on stochastic control and DP are briefly summarized. For more details, see, e.g., [11]. A large class of stochastic control problems deal with dynamics described by the following state equation:

where x(t) ∈ X is the state vector, u(t) ∈ u is the control input vector, and w(t) ∈ W is the process noise vector. Here, the noise vectors w(t) are generally assumed to be independent and identically distributed (IID). Many stochastic control problems are concerned with finding a time-invariant state-feedback control policy

that can optimize a performance index function. A widely used choice for the performance index function of infinite-horizon stochastic optimal control problems is the expected sum of discounted stage costs, i.e.,

where ℓ(· , ·) is the stage cost function. By minimizing this performance index function over all admissible control polices ？ : X → u, one can find the optimal value of J_？. This minimal performance index value is denoted by J^*, and an optimal state-feedback function achieving the minimal value is denoted by ？^*. The state value function V^*(z) is defined as the optimal performance index value conditioned on the initial state x(0) = z, i.e.,

According to optimal control theory [9,10], the state value function V^* : X → R is the unique fixed point of the Bellman equation

and an optimal control policy ？^* : X → u can be found by

In its operator form, the Bellman equation can be written as

where T is the operator (whose domain and codomain are both function spaces mapping X into R ？ {∞}) defined as

for any V : X → R ？ {∞}. The operator T for the Bellman equation is called the Bellman operator (see, e.g., [11]). As is well known, the state value function V^* and the corresponding optimal control policy ？^* cannot be solved exactly except in simple special cases [9,11]. An efficient strategy when finding the exact state value function is impossible is to rely on an approximate state value function

By applying this strategy to Eq. (20), one can find a suboptimal control policy ？^ads : X → u via

In this paper, we apply this ADP strategy to the constrained index tracking problem.

In this section, we describe constrained index tracking in the framework of a stochastic state-space control problem, and we present an ADP-based procedure to find a suboptimal solution to the problem. To express the constrained index tracking problem in a state-space optimal control format, we need to define the control input and state vector together with the performance index that is used as an optimization criterion. The control input we consider for the constrained index tracking problem is a vector of trades,

executed for the portfolio

y(t)？[y1(t),· · · , ym(t); yC(t)]T

at the beginning of each time step t. Note that u_i(t) represents buying or selling assets. That is, by u_i(t) ？ 0, we mean buying the asset associated with y_i(t), and by u_i(t) ？ 0, we mean selling it. For a state-space description of the constrained index tracking problem, we define the state vector as

With these state and input definitions, the state transition of Eq. (14) can be described by the following state equation:

where

As in [1], we assume that our stock prices are all normalized in the sense that initially they start from

A commonly used distance function for index tracking is the squared tracking error [1], i.e.,

Note that in this performance index function, both I(t) and w(t) are defined by means of the entries of the state vector x(t). For the initial portfolio, we take

which means that the tracking portfolio starts from the all-cash initial condition with a unit magnitude. With the above statespace description, the problem of optimally tracking the index, I(t), with the wealth of the tracking portfolio, w(t) = 1^T y(t), over the infinite horizon can be expressed as the following optimization problem:

In solving this index tracking problem, the tracking portfolio y(t) and the control input u(t) should satisfy certain constraints that arise naturally (e.g., no short selling or no overweighting in a certain sector [1,4]). The first constraint we consider in this paper is the so-called self-financing condition,

which means that the total money obtained from selling should be equal to the total money required for buying. Next, we impose a nonnegativity (i.e., long-only) condition for our tracking portfolio, i.e.,

for ∀i ∈ {1, · · · , m}, ∀t ∈ {0, 1, · · · }. As a final set of constraints, in this paper we consider the following allocation upper bounds:

where the κ_i fixed positive constants less than 1. By constraint #3, we mean that the fraction of the wealth invested in the m risky assets (i.e., stocks) should not be larger than κ₁. Also, constraint #4 sets a similar upper bound on specific stocks belonging to the set J. From these steps, the constrainedindex-following problem can now be expressed as the following stochastic control problem:

where I(t) = (1/n)1^Ts(t), w(t) = 1^T y(t), and x(t) = [s^T(t), y^T (t)]^T. Note that this formulation is a (slight) modification of the one used in [1,4], and the state vector x(t) = [s(t)^T, y(t)^T]^T here contains (slightly) richer information compared to the original one [1,4], which uses the stock prices and the total wealth of the tracking portfolio only. To solve the above constrained index tracking problem via ADP, we utilize the iterated-Bellman-inequality strategy proposed by Wang, O’Donoghue, and Boyd [11,12]. In the iterated-Bellmaninequality strategy, convex quadratic functions

are used for approximating state value functions, and letting parameters of the

satisfy a series of Bellman inequalities

with

guarantees that

is a lower bound of the optimal state value function V^* [11,12].

In this paper, we obtain an ADP-based solution procedure for the constrained index tracking problem of Eq. (36) utilizing the iterated-Bellman-inequality strategy [11,12]. To compute the stage cost, we note that since the initial stock prices and the initial cash amount are both normalized (i.e., s₁(0) = · · · = s_n(0) = 1 and y_C(0) = 1), the initial tracking error I(0) - W(0) is equal to zero. Hence, the performance index can be equivalently written as

For simplicity and convenience, we use the first term on the right-hand side of Eq. (39) as our new performance index function, i.e.,

Now we consider the tracking error at time t + 1 conditioned on x(t) = z and u(t) = v. For notational convenience, we let z ？ [s^T, y^T]^T , and we define s^a, s^b, y^a, and v^a as follows: s^a ？ [s₁, · · · , s_m]^T, s^b ？ [s_m+1 · · · , s_n]^T, y^a ？ [y₁, · · · , y_m]^T, and v^a ？ [v₁, · · · , v_m]^T. Note that, with these definitions, we have

Then the tracking error I(t + 1) ？ W(t + 1) conditioned on x(t) = z and u(t) = v satisfies the following:

Based on this equality, one can obtain an expression for the stage cost, i.e., the expectation of the squared tracking error at time step (t + 1) conditioned on

as follows:

where

Note that here the μ_i and the Σ_ij are the block components of μ and Σ, respectively, i.e.,

Now we let the derived matrix variables G_i, i = 1, · · · , M, satisfy the following:

Here, the expectation in the right-hand side is equal to

Then, by evaluating the right-hand side of Eq. (47), we obtain

where

In Eq. (49), the P_i,jk and the p_i,j are the block components of P_i and p_i, respectively, i.e.,

and ？ denotes the elementwise product.

Note that the constraints considered in this paper are all linear. Hence, the left-hand sides of our constraints can be expressed as

More specifically, the first constraint can be written as

where E⁽¹⁾ = 1_1×(m+1) and F⁽¹⁾ = 0_1×(n+m+1). Further, the linear inequality constraints can be given in the form

where

Note that, in Eq. (54), the allocation constraint set J is described by {j₁, · · · , j_|J|}, where |J| is the number of entries in J . Also, note that here e_j means the jth column of the identity matrix I_m. With all these constraints required for the input-state pair (v, z), the resultant constrained Bellman inequality condition becomes the following: Whenever (v, z) satisfies

we must have

where S_i？1 is the derived matrix variable defined by

Finally, note that one can obtain the following sufficient condition for the constrained Bellman inequality requirement in Eqs. (55) and (56) using the S procedure [15]:

where the

are S-procedure multipliers (with appropriate dimensions) [15], and

By combining all the above steps together, the process of finding a suboptimal ADP solution to the constrained index tracking problem can be summarized as follows:

[Procedure]

Preliminary steps:

1. Choose the discount rate γ and the allocation upper bounds κ1 and κ2.

2. Estimate μ, Σ, and rf .

Main steps:

1. Initialize the decision-making time t = 0, and let x(0) = [1, · · · , 1, 0, · · · , 0, 1].

2. Compute the stage cost matrix L of Eq. (43) and the Λ^(k) of Eq. (59).

3. Observed the current state x(t), and set z = x(t).

4. Define LMI variables:

(a) Define the basic LMI variables, Pi, pi, and qi of Eq. (37).

(b) Define the derived LMI variables, Gi of Eq. (48) and Si of Eq. (57).

(c) Define the S-procedure multipliers,

of Eq. (58).

5. Find an approximate state value,

by solving the following LMI optimization problem:

6. Obtain the ADP control input, u(t), as the optimal solution V^* of the following quadratic program:

and trade accordingly.

7. Proceed to the next time step, i.e., t ← (t + 1).

8. (optional) If necessary, update μ, Σ, and r_f .

9. Go to step 2.

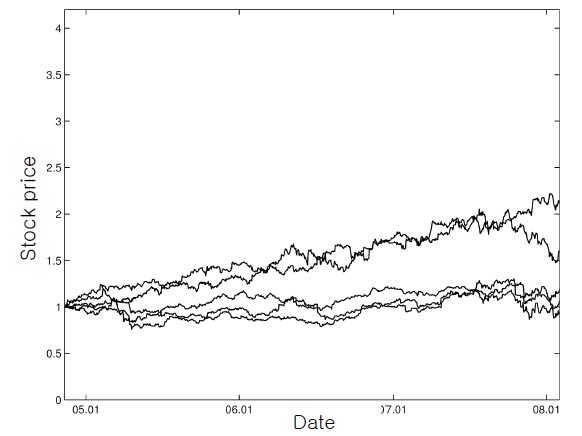
In this section, we illustrate the presented ADP-based procedure with an example of [1], which dealt with daily prices of five major stocks from November 11, 2004, to February 1, 2008. The index I(t) in the example was defined based on IBM, 3M, Altria, Boeing, and AIG (the ticker symbols of which are IBM, MMM, MO, BA, and AIG, respectively). Their stock prices during the considered test period are shown in Figure 1.

As the subset comprising the tracking portfolio, the first three stocks, s₁, s₂, and s₃ (i.e., IBM, MMM, and MO) were chosen. Note that n = 5 and m = 3 in this example. During the test period, the ADP-based tracking portfolio was updated every 30 trading days. In this update, the mean return vector μ and the covariance matrix Σ were estimated by averaging the past daily raw data via the exponentially weighted moving average (EWMA) method with the decay factor λ = 0:999. For the riskfree rate, we assumed

as in [1]. Between each 30-day update, the number of shares in the tracking portfolio remained the same. The ADP discount factor was chosen as γ = 0:99.

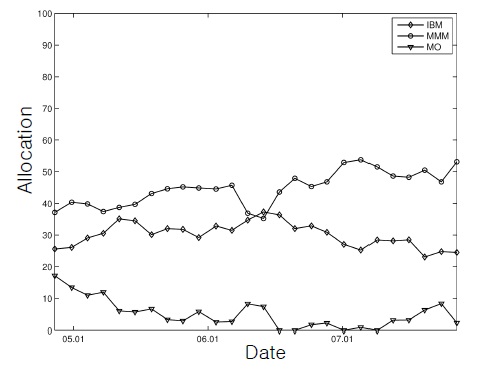
As described in Section 3, the performance index function was computed based on the mean-square distance between the index and the portfolio wealth. Finally, the allocation upper bound was considered for the first stock (i.e., J ={IBM}).

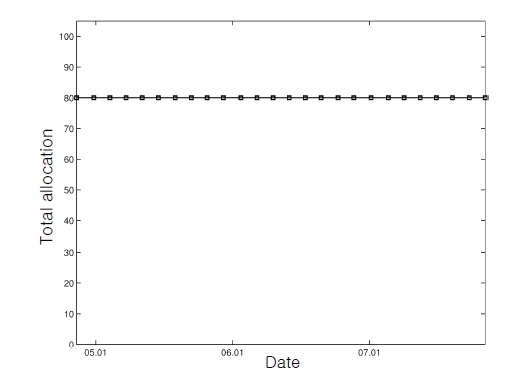
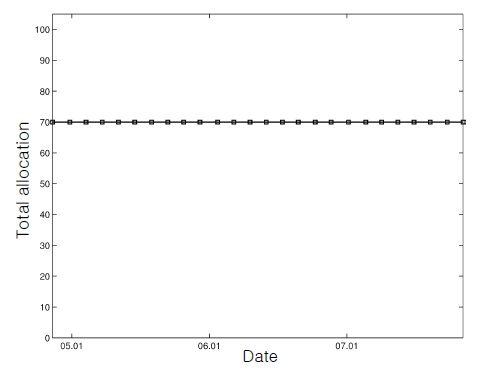
We considered two scenarios with different constraints (Table 1). As shown in Table 1, trading has more severe constraints as the scenario number increases. In the first scenario, we traded with fundamental requirements (i.e., self-financing and a nonnegative portfolio) and the total allocation bound constraint (i.e., Constraint #3). For the upper bound constant for constraint #3, we used κ₁ = 0:8. This bound means that the total investment in the three stocks (IBM, MMM, and MO) was required to be less than or equal to 80% of the total portfolio value. The control inputs obtained by the ADP procedure are shown in Figure 2. Applying these control inputs, we obtained the simulation results of Figures 3-5. Figure 3 shows that the ADP-based portfolio followed the index closely in Scenario #1. Figure 4 shows that the 80% upper bound condition for the total allocation in stocks was well respected by the ADP policy in Scenario #1. The specific portion of each stock in the tracking portfolio is shown in Figure 5.

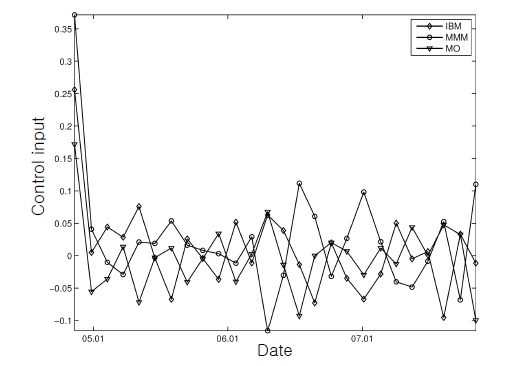
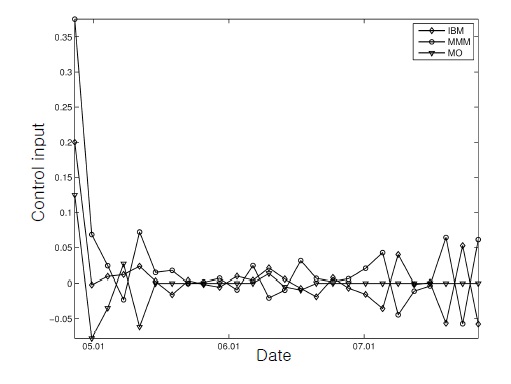
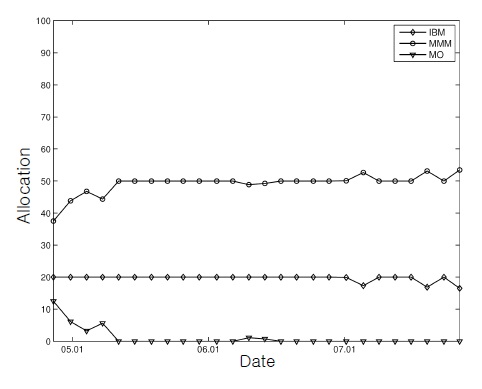
This figure, together with Figure 2, shows that the control inputs changed the initial cash-only portfolio rapidly into the stock-dominating positions for successful tracking.

In the second scenario, more difficult constraints were imposed. More specifically, the κ₁ value was reduced to 0:7, and the allocation in the first stock (i.e., IBM) was required not to exceed 20% of the total portfolio wealth. The control inputs and simulation results for Scenario #2 are shown in Figures 6-9.

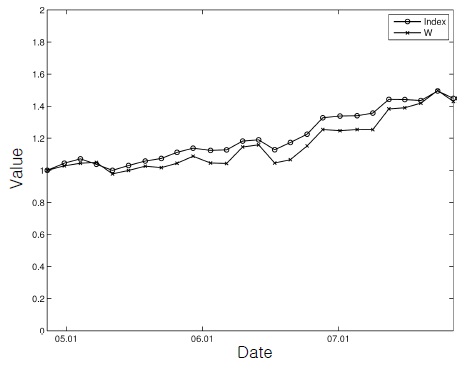
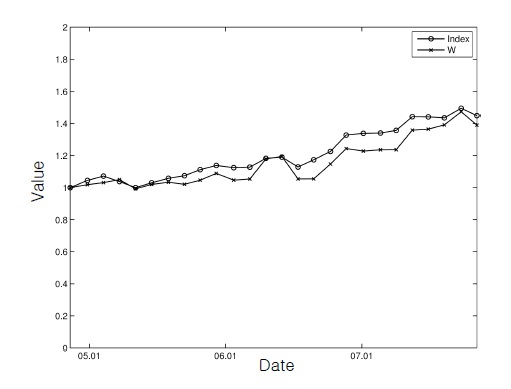
These figures show that, although the tracking performance was a little degraded owing to the additional burden, the wealth of the ADP-based portfolio followed the trend of the index most of the time reasonably well with all the constraints being respected.

The constrained index tracking problem, in which the task of trading a set of stocks is performed so as to closely follow an index value under some constraints, can be viewed and formulated as an optimal decision-making problem in a highly uncertain and stochastic environment, and approaches based on stochastic optimal control methods are particularly pertinent. Since stochastic optimal control problems cannot be solved exactly except in very simple cases, in practice approximations are required to obtain good suboptimal policies. In this paper, we studied approximate dynamic programming applications for the constrained index tracking problem and presented an ADP-based index tracking procedure. Illustrative simulation results showed that the ADP-based tracking policy successfully produced an index-tracking portfolio under various constraints. Further work to be done includes more extensive comparative studies, which should reveal the strengths and weaknesses of the ADP-based index tracking, and applications to other types of related financial engineering problems.

No potential conflict of interest relevant to this article was reported.