The QH beams which can be generated by SLMs have been studied and used widely in recent years [1]. The coherence and polarization properties of quasi-homogenous sources in the far field has been studied by Korotokva [2]. The coherence of properties of the field generated by a beam radiated from a quasi-homogenous electromagnetic source scattering on QH media has been studied by Xin [3]. Chen and Li have been researched the coherence properties and polarization modulation of QH beams scattered from anisotropic media [4-5]. The propagation properties of laser beams in random media like turbulence or human tissue are important for applications such as optical imaging, remote sensing and communication systems so more and more researchers are attracted [6-11]. The polarization “self-reconstructed” phenomenon in atmosphere turbulence has been known for a long time. The normalized spectrum of the beam generated by QH source after propagating through turbulent media has been proved to be equal to the normalized spectrum of the source [12]. The degree of polarization of electromagnetic Gaussian-Schell beams and partially coherent electromagnetic flat-topped beams also have self-reconstructed properties in atmospheric turbulence [13-14]. However, recent reports have shown that beams generated from anisotropic sources don’t have polarization self-reconstructed properties in turbulent media [15-16]. On the other hand, oceanic turbulence is an important natural random medium but the light propagation though oceanic turbulence is a relatively unexplored topic compared to that in other media. The spatial spectrum model of oceanic turbulence combining temperature and salinity fluctuations is only used by a few articles to study the light propagation in the oceanic waters [16-18].

In this paper, we focused on the polarization features of QH beams propagating through oceanic turbulence. The analytical expressions of on-axis generalized Stokes parameters of QH beams were calculated，then the variations of DOP and SOP of QH beams traveling through oceanic turbulence have been simulated. The self-reconstructed properties of such beams in the far field in turbulent media have been analyzed under different source parameters and turbulence conditions.

For beams generated by quasi-homogenous (QH) sources the spectral density S⁽⁰⁾(r) varies much more slowly with position vector than the correlation coefficients μ_ij⁽⁰⁾(r,ω) change with difference of position vector r₁-r₂. The cross spectral density matrix of QH sources can be expressed as:

The superscript (0) denotes quantity pertaining to the incident field. The spectral density can be expressed as the trace of cross spectral density matrix:

(r₁,r₂,ω), a_ij(ω) is the frequency dependent factor which connects the spectral components: S_y⁽⁰⁾(ω)=α (ω)S_χ⁽⁰⁾(ω).

For α =0, the source generated linearly polarized light in the x direction, for α →∞, the light is linearly polarized in the y direction. Without loss of generality, the spectral density and correlation coefficients can be described by the Gaussian-Schell model:

A is spectral amplitude which we set A=1 in this article, and B_ij is called the coefficient of correlation between the incident field components, for quasi-homogenous beams, it can be set as: B_xx=B_yy=1, B_xy=B^*_yx, where the asterisk means complex conjugate. σ represents the width of the source, δ_ij represents the coherent width of the source. Several conditions of the source must be satisfied in order to produce a physically reliable QH beam [19].

The cross spectral density matrix of the beam at the receiving plane can be derived by the extended Huygens- Fresnel principle:

Where r₁, r₂ are two arbitrary position vectors of points on the source plane while ρ₁, ρ₂ are two position vectors of observation points on the receiving plane. z is propagation distance and

is the wave number of the beam. The last term in Eq. (5) represents the correlation function of the complex phase perturbed by random media：

Where

describes the strength of turbulence perturbation.

The model of the spatial power spectrum of refractive index fluctuations of homogenous and isotropic oceanic turbulence can be described as a linearly polynomial of temperature fluctuations and salinity fluctuations:

In Eq. (7), ξ is the rate of dissipation of kinetic energy per unit mass of fluid, ranging from 10^-4m²s^-3 in turbulence surface layer to 10^-10m²s^-3 in the mid-water column. χ_T is the rate of dissipation of mean squared temperature ranges from 10^-2K²s^-1 below the oceanic turbulence to 10^-10K²s^-1 at the mid-water column. η is the Kolmogorov micro scale. Other parameters in Eq. (7) are:

A_T = 1.863×10^-2, A_S = 1.9×10^-4, A_TS =9.41×10^-3, δ = 8.284(κη)^4/3 + 12.978(κη)² ; w defines the ratio of temperature to salinity contributions to refractive index spectrum which in oceanic waters varies in the interval [-5;0], with -5 and 0 corresponding to dominating temperature-induced and salinityinduced optical turbulence, respectively.

From Eq. (3)-Eq. (6), the cross spectral density matrix of the electromagnetic field on the receiving plane can be expressed as:

As a matter of convenience, we make changes of the spatial arguments:

With the help of Eq. (9), the cross spectral density matrix on the receiving plane is derived:

Where

The polarization properties of an electromagnetic beam at a point in space can be determined by use of Stokes parameters which have recently been generalized from one-point quantities to two-point counterparts [20]. They contain not only polarization properties but also coherence properties of beams [21] and can be measured by Young’s interference experiment [22-23]. The changes of generalized Stokes parameters in optical system or random media are also interesting problems and have received a lot of attention [24-25]. The four parameters can be expressed as follows:

where

are Pauli spin matrices:

represents the cross-spectral density matrix (CSDM) of the beam:

If we only considered polarization properties of one point, i.e., ρ₁=ρ₂=ρ, From Eq. (10), each element of the CSDM can be derived as the expression of:

Inserting Eq. (11) into Eq. (12), and using the conditions of M_xy=M_yx, α_xy=α_yx the analytical expressions of four Stokes parameters can be obtained:

The polarization properties can be expressed as the functions of these four parameters.

We considered the degree of polarization and the state of polarization of QH beams in this paper. DOP is used to describe the polarized portion of a beam. DOP=1 means perfectly polarized beam while DOP=0 means unpolarized beam. The state of polarization (SOP) includes the azimuth angle and ellipticity. The azimuth angle θ is defined by the smallest angle formed by the positive x-direction and the direction of major semi-axis of the ellipse. ε , which determines the shape of the ellipse, is the ratio of the major semi-axis and the minor semi-axis.

For convenient, we normalized three Stokes parameters by S₀ as:

The DOP and SOP can be expressed as the function of normalized Stokes parameters:

Because of the uniform polarization properties of quasihomogenous beams, we only need to consider the on-axis point of the beam. And in order to prove the polarization self-reconstructed properties of QH beam, we should study far-field polarization properties of normalized Stokes parameters. First, let’s consider the limit as follow:

Where s_i(0, z, ω) are normalized Stokes parameters on the receiving plane while s_i(0, 0, ω) are such parameters on the source plane. From Eq. (13),

can be obtained from Eq. (1) - Eq. (4). Then substituting into the limit of the ratio of two parameters, we get:

In turbulent medium,

so F=1, then we proved the self-reconstructed property of s₁. Other parameters in Eq. (14) can also be proved similarly, then DOP and SOP self-reconstructed properties can be derived directly. We set follow parameters to judge the ability of the self -reconstructed property of QH beams:

These parameters are modulus values of relative difference of the on-axis DOP and SOP between the source plane and the receiving plane at a special distance z in turbulences, the self-reconstructed ability will be better when these values get closer to 0.

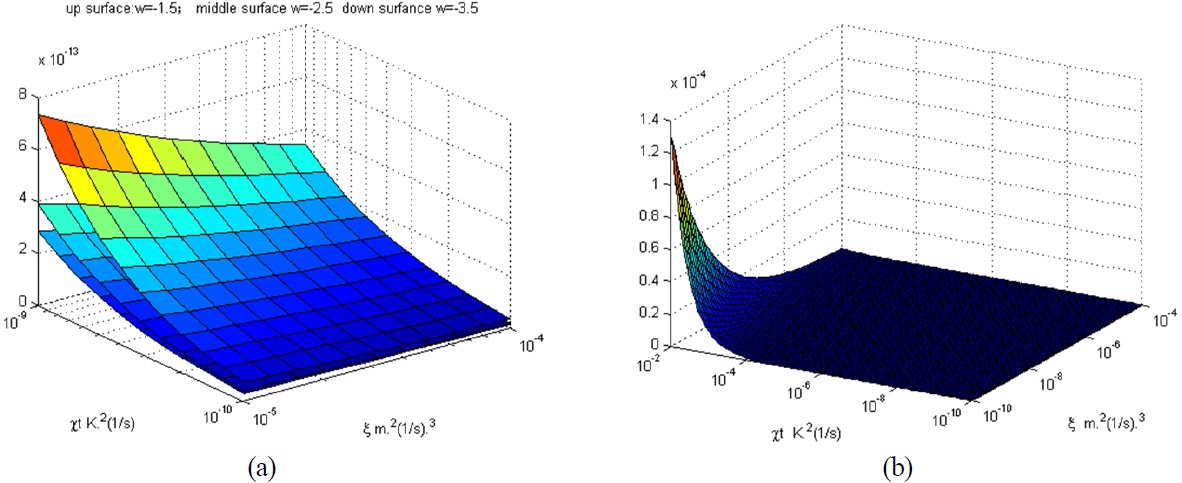
Figure 1 shows the strength of oceanic turbulence changes with turbulence parameters: w, χ_T and ξ . It can be easily found out that the strength of turbulence T increases with the increase of χ_T and w, but reduces with the increases of ξ.

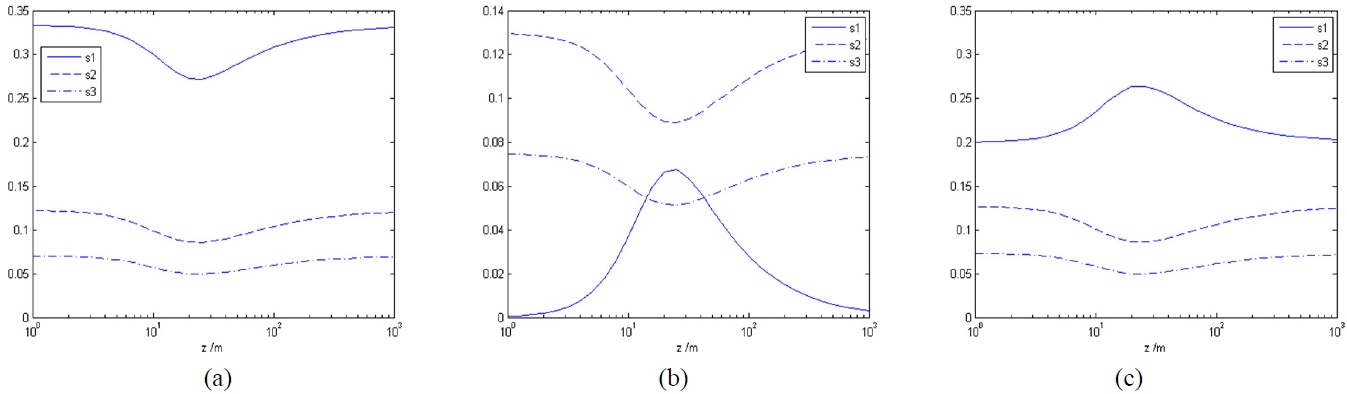
Figure 2 shows the changes of normalized Stokes parameters with distance at different a. The DOP and SOP we calculated in Eq. (17) and Eq. (19) could be expressed as the function of these parameters, so the behavior of generalized Stokes parameters decides the evolution of DOP and SOP of the beam through propagation.

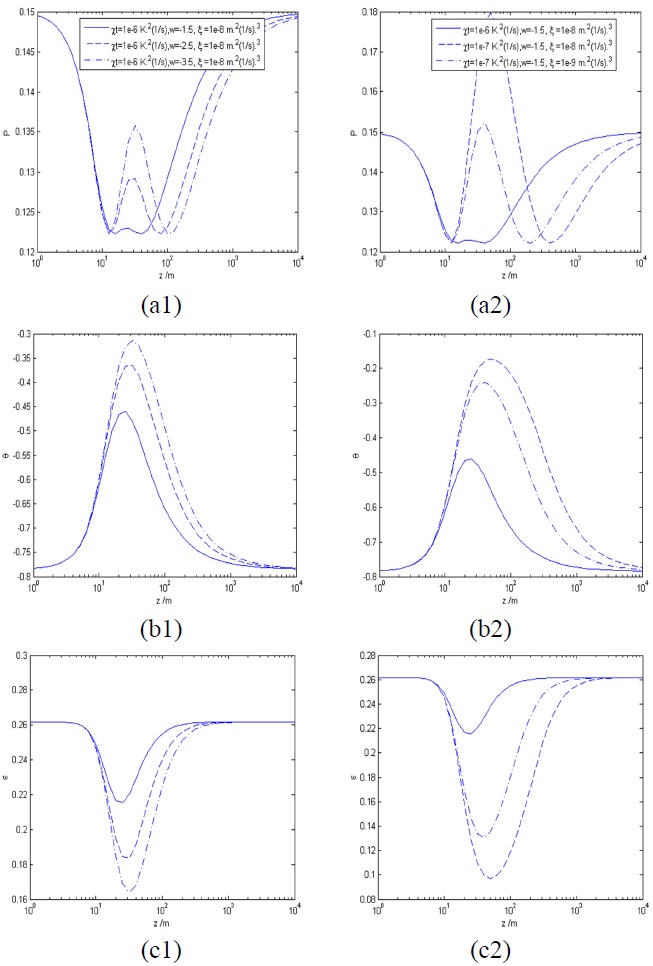
In Fig. 3, we illustrated how the DOP and SOP of the QH beams depend on the parameters of oceanic turbulence. The effect of w on the changes of DOP and SOP has been shown in Fig. 3(a1)-(a3) and the effect of χ_T and ξ has been shown in Fig. 3(b1)-(b3).

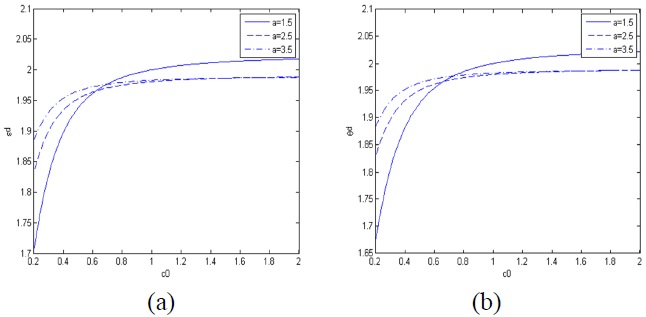
In Fig. 4, the influence of coherent width and the coefficients α_ij(ω) on the changes of self-reconstructed properties of DOP of QH beams were revealed. While δ_yy and δ_xx are kept fixed, c₀ is the coefficient to decide the value of δ_xx as the form δ_xx = c₀δ_xy.

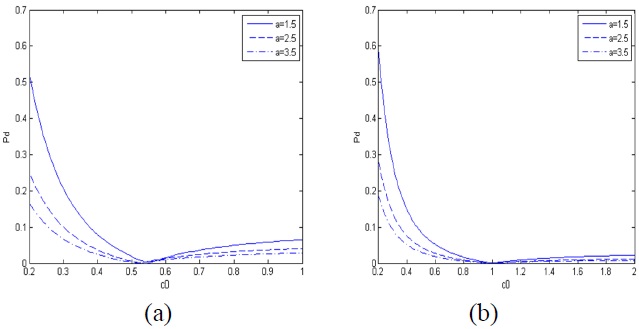
In Fig. 5, the self-reconstructed behavior of azimuth angle θ and the degree of ellipticity ε were judged as the same method of DOP we plotted their variation versus c₀.

(1) Both DOP and SOP fluctuate at the range of 0.01 km1 km. DOP and SOP get more fluctuations in weak turbulence and get larger self-reconstructed distance than that in strong turbulence.

(2) S₂ and S₃ in ocean waters fluctuate less than S₁ during the propagation but they will all reach the initial value if the propagation distance is long enough.

(3) DOP varies with more complexity with distance in ocean waters than SOP. The self-reconstructed distance of both decreases with the increase of χ_t and w, but increases with the increases of ξ .

(4) When δ_yy=δ_xy, P_d reaches the minimum value, and it’s almost equivalent for different α ，but if δ_xx≠δ_xy, as what have shown in Fig. 4(b), P_d will get to minimum value at different c₀ for different α.

(5) ε_d and θ_d increase as increases but will change slowly when c₀>1. It means when other parameters are kept fixed, the coherence width δ_xx should be controlled to be smaller than δ_xy in order to obtain better SOP self-reconstructed properties, but these two variables of SOP have no minimum values with the variation of c₀.

According to our analysis, the normalized Stokes parameters will be affected by temperature and salinity fluctuations so the DOP and SOP will also be affected. And s₁ fluctuates much more than s₃ and s₃, DOP varies with more complexity than SOP. Furthermore, both of normalized generalized Stokes parameters of QH beams have proved to be equal to the initial value if the propagation distance is long enough, so the self-reconstructed properties of DOP and SOP of such beams can also be proved. The choice of coherence width of the QH beams can help us to get the best self-reconstructed ability of DOP, but for two parameters of SOP, there are no best choices of these parameters. Our work may be helpful to develop underwater optical imaging or communication system.