Liquid crystal panels (LCPs) are optoelectronic devices that can modulate the state of light. They are used for many practical applications including flat panel display, holography and optical information processing because of their inherent ability to spatially modulate a light beam in a programmable manner [1-4]. Twisted nematic (TN) type LCP spatial light modulators (SLMs) are good for intensity modulation and parallel aligned LCP SLMs are suitable for phase modulation. Some application areas of SLMs such as ultra-short laser pulse control require phase modulation [5,6]. However parallel aligned LCP SLMs are expensive, while TN-LCP SLMs are relatively low-cost and easily available. This is why much effort has been made to use TN-LCP SLMs for many applications [7,8].

For programmable operation of a TN-LCP spatial light modulator (SLM), the Jones matrix of the TN-LCP needs to be determined accurately. However, manufacturers do not usually provide that information, and the user must determine the matrix. According to the literature, the TN-LCP can be considered as a stack of thin slices acting as homogeneous uniaxial crystals [9]. The Jones matrix of a homogeneous uniaxial crystal slice can be written as a function of its ordinary and extraordinary indices of refraction as well as the orientation angle of the liquid crystal molecules [9]. The Jones matrix of the whole TN-LCP can be described as the product of the individual Jones matrices of each homogeneous uniaxial crystal slice [10]. According to the approximation, the Jones matrix of the whole TN-LCP can be written as

Here c₁ is a constant used to define the intensity loss, i is

and Δ？ is the phase change induced by the LCP at a given wavelength. The matrix describes the change in polarization state of the incoming beam. The goal of this study is to determine the signs as well as the absolute values of the matrix elements can be determined by polarimetric methods experimentally, but it has been thought that the signs of the elements can not be determined uniquely by polarimetric methods only. However it has been shown that the signs can be determined by polarimetric methods [11].

In this paper, we demonstrated a polarimetric method for unambiguous determination of signs of the Jones matrix elements. By measuring the transmittance with an optical system of polarizer-LCP-analyzer, we obtained the set of the unitary matrix elements. In addition, by measuring the transmittance after inserting a quarter wave plate in the system, we obtained another set of unitary matrix elements. By comparing two sets of unitary matrix elements, we could determine the unitary matrix elements accurately without the sign ambiguity.

Our method has some advantages with respect to other previous similar methods. First, our method improved the accuracy. In particular, polarizer and analyzer rotate in the same and opposite directions with 1degree angular increment from 0° to 180°, so Jones matrix elements were obtained from fitting a trigonometric function with many data points. Also, our method uses only two rotating elements (polarizer and analyzer) and except for the rotation of the polarizers the alignments of all the other optical elements were not disturbed during the measurement, which can reduce potential errors due to realignment.

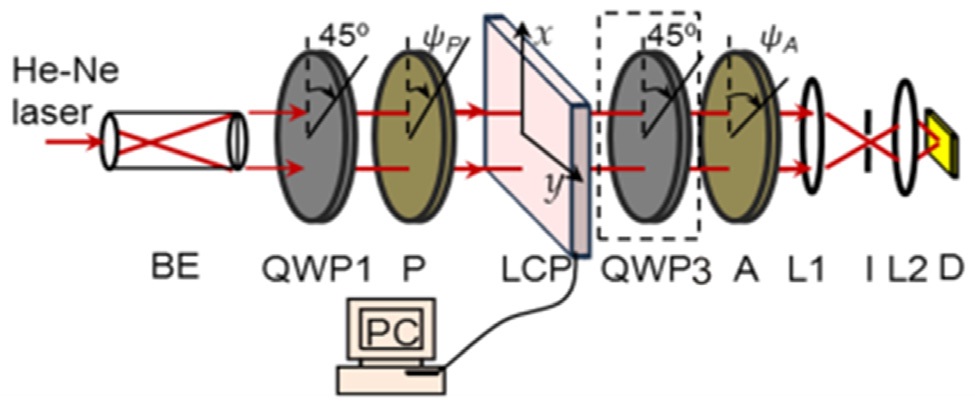
The polarimetric method to determine the Jones matrix is based on the transmittance measurement of the optical system. Let us first explain how to calculate the transmittance of the optical system. Our whole optical system consists of a He-Ne laser light source, a quarter wave plate (QWP1), polarizer (P), TN-LCP, analyzer (A) and a silicon photo-diode detector as shown in Fig. 1.

First we considered the transmittance intensity of the optical system consists of a light source, a quarter-wave plate (QWP1) and a polarizer. The laser light source was linearly polarized, so the QWP1 was used to make the linearly polarized light into the circularly polarized light. The circularly polarized light was the input beam of the polarizer. The azimuth angle of the polarizer was defined as ψ_P. The relation between the Jones vector of the input beam (a, b ？ e^iδ ) and that of the output beam (x_out1, y_out1) for the optical system can be written as Eq. (2)

Here a and b are the electric field components on the vertical (x, z) and horizontal (y, z) planes, respectively. δ is a phase difference between the electric field components. Q(π/4) is the Jones matrix of the QWP1 whose fast axis was aligned 45° with respect to the vertical (x) axis. P(ψ_P) is the Jones matrix of the polarizer whose azimuthal angle is ψ_P. The output beam intensity was determined by following equation,

The laser light was almost linearly polarized in the vertical (x, z) plane, so the electric field components satisfied a condition, a >> b.

We calculated the transmittance intensity of the whole optical system consists of a light source, a quarter-wave plate (QWP1), a polarizer, a TN-LCP and an analyzer. The TN-LCP was placed between a polarizer and an analyzer whose azimuth angles were ψ_P and ψ_A, respectively. The output beam of the polarizer described in Eq. (2) was used as the input beam of the later optical system. The Jones vector of the output beam for the whole optical system can be written as Eq. (4).

We defined the transmittance of the optical system composed of TN-LCP and analyzer, T_ψP, _ψA, as the relative ratio between the output (I) beam intensity of Eq. (5) and the input beam intensity (I₁) of Eq. (3). T_ψP, _ψA can be expressed as Eq. (7),

Here c₃ is a constant.

The optical system used in our study was shown in Fig. 1. The light source was a linearly polarized He-Ne laser. The laser beam was expanded by using the beam expander (BE) and then was sent to the quarter wave plate (QWP1). The quarter-wave plate made the linearly polarized light circularly polarized. The circularly polarized beam was directed to a rotating linear polarizer (P) and then was sent to the sample. The polarization state of the transmitted beam was investigated with an analyzer (A) and an additional quarter wave plate (QWP3). The intensity of the beam passed through the analyzer was measured with the photodiode (D). A quarter-wave plate (QWP2) and a TN-LCP SLM (Holoeye LC2002, SONY LCX016AL-6) were used as samples.

The transmittance of the optical system (sample + analyzer) depends only on the sum (ψ_A+ψ_P) and the difference (ψ_A-ψ_P) of the angles of the polarizer and analyzer. After substituting φ=ψ_A - ψ_P and ψ=ψ_A + ψ_P into Eq. (7), the transmittance of the optical system, T_{φ, ψ} takes a simpler form.

Here C is a constant. φ₀, ψ₀ are the initial phases of the trigonometric functions and A, B are the amplitudes of the functions. A set of transmittance T_{φ, ψ} data was collected by changing φ and ψ from 0° to 360°. The coefficients A and B, also the initial phase angles φ₀ and ψ₀ in Eq. (8) were determined by the Newton-Raphson fitting method.

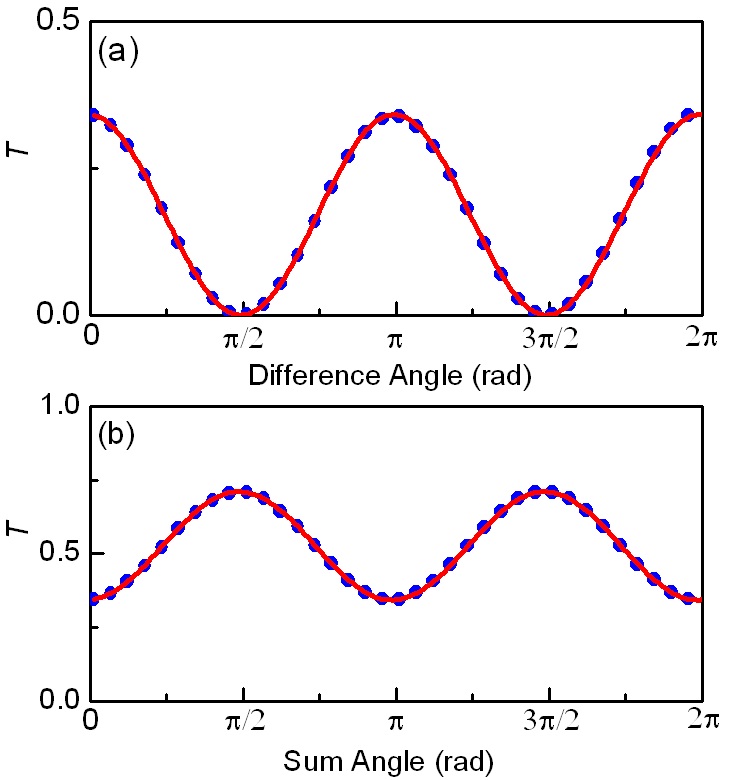
To check the validity of our method, the Jones matrix elements of a quarter wave plate (QWP2) is experimentally determined and compared with the theoretical one. The fast axis of the QWP2 is set to make 45º with the x axis. If the quarter-wave plate is ideal, then the Jones matrix should be

from Eq. (1), where c₄ is the constant representing the intensity loss. The matrix should be unitary, so the elements f, h, g and j should satisfy the condition, f ² + h² + g² + j² = 1. To satisfy the constraints f, j, h and g should be

h = g = 0. Eqs. (6), (7), and (8) show that f, j, h and g are connected to the coefficients A and B also the initial phase angles φ₀ and ψ₀ of the trigonometric functions representing the transmittance of the optical system, i.e.

The transmittance T_{φ, ψ} of the quarter-wave plate (QWP2) and the analyzer was measured and fitted with Eq. (8) to determine A, B, φ₀ and ψ₀. To make Eq. (8) simpler, some conditions are chosen to make the cosines of the sum and the difference of the angles constant. First the analyzer and polarizer rotated in the opposite direction with same angle increment, so that the ‘sum angle (ψ_A+ψ_P)’ is set to be zero, i.e. ψ=ψ_A+ψ_P=0. Then the transmittance as a function of the difference angle φ=ψ_A-ψ_P is measured as presented in Fig. 2(a). By fitting the data points with a

cosine function, the information about f and h is obtained.

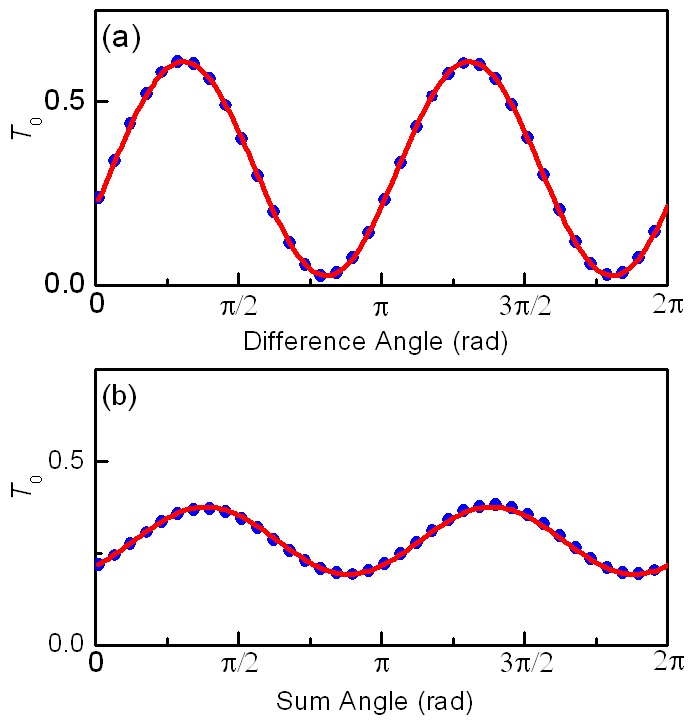
Similarly, the analyzer and the polarizer are rotated in the same direction with the same angle increment so that the ‘difference angle (ψ_A-ψ_P)’ is set to be zero, i.e. φ=ψ_A-ψ_P=0. Then the transmittance as a function of the sum angle ψ=ψ_A+ψ_P is measured as presented in Fig. 2(b). By fitting the data points with a cosine function, the information about g and j is obtained.

It should be noted however that, the relative signs of g and j elements to those of f or h were not uniquely defined because of the ambiguity of the phase of the trigonometric functions φ₀ and ψ₀ in Eq. (10).

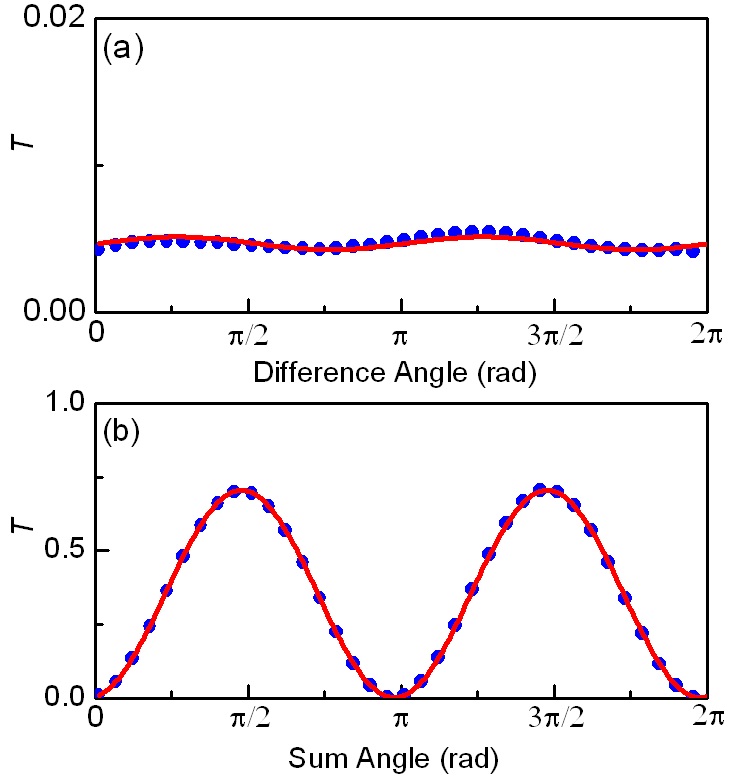
To eliminate the sign ambiguity, an additional quarter-wave plate (QWP3) was inserted between the quarter-wave plate (QWP2) and the analyzer. The fast axis of QWP3 was aligned 45° with respect to the x axis. Including the contribution of the QWP3, the transmittance became a function of φ and ψ as shown in Eq. (11).

Here c₅ is a constant. m, q, p and l were connected to f, h, g and j by comparing Eq. (11) with Eq. (6). As a result,

Also the sum of the squares of the new elements should

satisfy m² + q² + p² + l² = 2 because of the unitarity.

To determine m, p, q and l, first the analyzer and the polarizer are rotated in the opposite directions with the same angle increment so that the sum angle remains zero, i.e. ψ=ψ_A+ψ_P=0. The transmittance as a function of the difference angle φ=ψ_A-ψ_P is presented in Fig. 3(a). By data fitting, the information about m and q is obtained. Similarly, the analyzer and the polarizer are rotated together so that the difference angle remains zero, i.e. φ=ψ_A-ψ_P=0. Then the transmittance as a function of the sum angle ψ=ψ_A+ψ_P is presented in Fig. 3(b). By data fitting, the information about p and l is obtained.

The sign of the f, g, j, and h can be determined by comparing four element values of the first method (without QWP3) with four element values of the second method (with QWP3). The experimentally obtained Jones matrix elements of QWP2 are f = 0.706, j = 0.707, h = -0.017 and g = 0.026 consistent with the theory, which confirms the validity of our method.

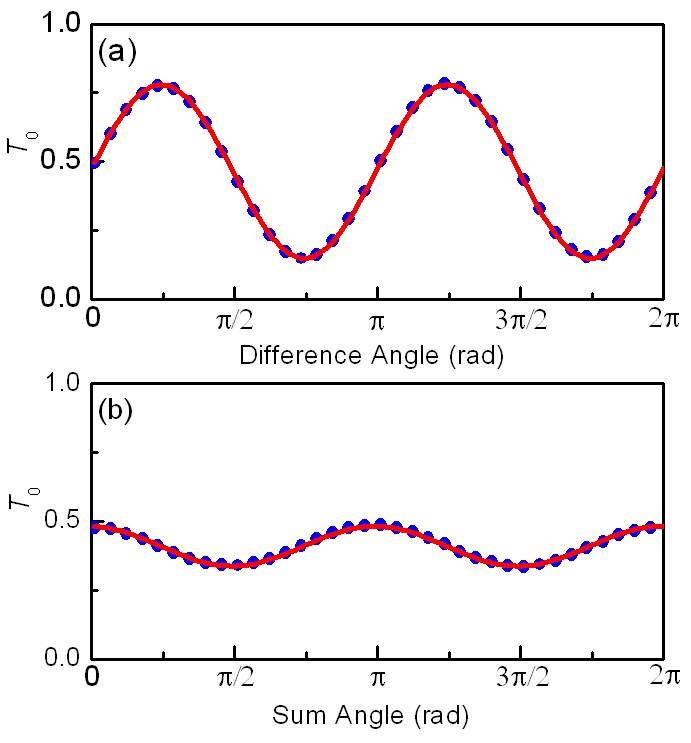
The same method was used to determine the Jones matrix elements of a programmable TN-LCP SLM. A programmable TN-LCP SLM was installed between the polarizer and analyzer as shown in Fig. 1. The TN-LCP can change the intensity and the phase of the input beam as the grey level is controlled by an external device. The corrected transmittances T₀ of the TN-LCP and the analyzer for several different grey levels were measured. The meaning of the corrected transmittance T₀ will be discussed in subsection 4.3. Fig. 4 shows the difference angle (φ=ψ_A-ψ_P) and the sum angle (ψ=ψ_A+ψ_P) dependence of the T₀ for

one of the grey levels (grey level 192 of our LCP device). As demonstrated for the quarter-wave plate (QWP2) case, the absolute values of the f, g, j, and h of the Jones matrix were determined by fitting the transmittance with Eq. (8).

To determine the signs of the Jones matrix elements, additional set of data were measured. Fig. 5 shows the sum angle (ψ=ψ_A+ψ_P) and the difference angle (φ=ψ_A-ψ_P) dependence of T₀. Note that additional quarter-wave plate QWP3 was inserted between the TN-LCP and the analyzer for obtaining the data set. The absolute values of the m, q, p, and l of the Jones matrix were determined by fitting the transmittance with the Eq. (11).

The sign of the f, g, j, and h can be determined by comparing four element values of the first method (without QWP3) with four element values of the second method (with QWP3). The experimentally obtained Jones matrix elements of TN-LCP (at grey level 192 of our LCP device) were f = 0.64, h = 0.63, g = -0.44 and j = -0.02. The matrix elements of other grey levels can be obtained similarly.

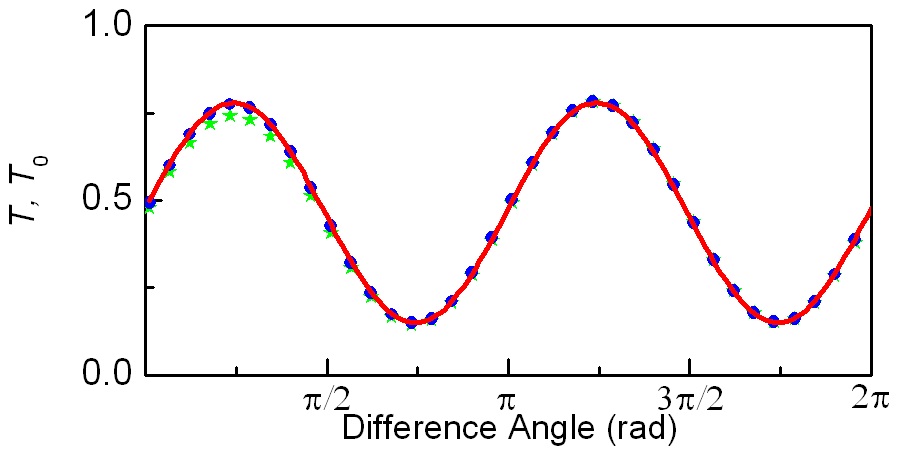
There is discrepancy between the theoretical transmittances described by Eqs. (8) and (11) and the measured transmittance. Such discrepancy is negligible for the quarter-wave (QWP2), but is not negligible for the TN-LCP. Fig. 6 shows the measured transmittance (T, solid asterisks) of TN-LCP, the error-corrected transmittance (T₀, solid circles), and the theoretical fitting function (solid line). They do not overlap perfectly and the discrepancy is especially large around the π /4 of the difference angle.

The intensity loss occurred at the TN-LCP is the most

dominant reason of the discrepancy. The intensity loss can be caused by many factors including absorption, scattering or reflection. However, the intensity loss does not affect the fitting process significantly in our method.

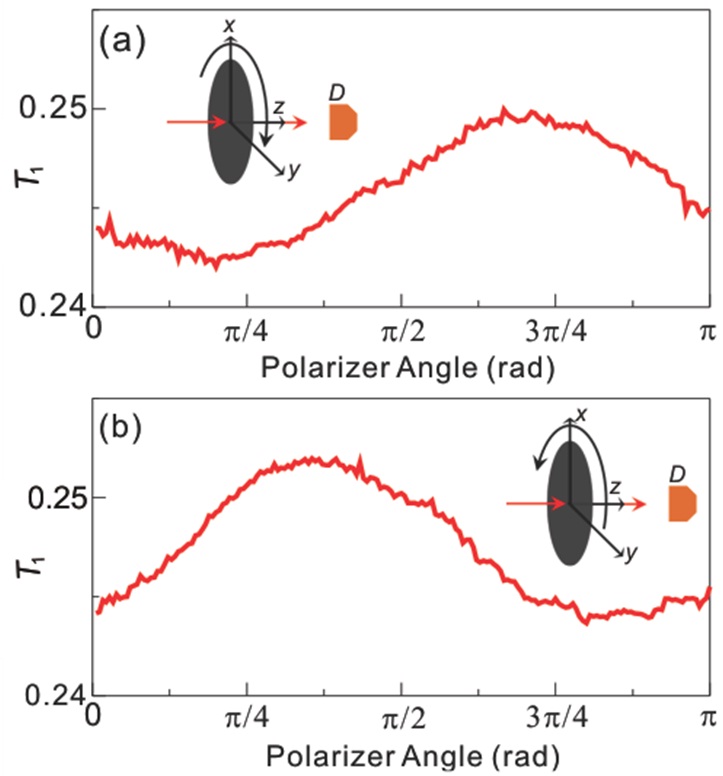
Figure 7 shows the polarizer angle dependence of the transmittance of the TN-LCP (T₁). Note that T₁ was measured without the analyzer and the additional quarter-wave plate QWP3. There are two polarizer rotation directions. Fig. 7(a) shows the T₁ for the clockwise polarizer rotation (See the inset of Fig. 7(a)). This corresponds to the polarize rotation for the difference angle (φ=ψ_A-ψ_P) measurement case shown in Figs. 4(a) and 5(a). Fig. 7(b) T₁ for the counter-clockwise polarizer rotation (See the inset of Fig. 7(b)). This corresponds to the polarize rotation for the sum angle (ψ=ψ_A+ψ_P) measurement case shown in Figs. 4(b) and 5(b). The T₁ data show the oscillating behavior deviated from the constant value about 2%.

The final transmittance (T) of the whole optical system can be considered as the multiplication of the T₁ and the transmittance (T₀) of the analyzer (or analyzer + the additional quarter-wave plate QWP3, when QWP3 is inserted). To remove the polarizer dependence in the final transmittance of the whole optical system the transmittance T was divided with transmittance (T₁) of TN-LCP. This is the corrected transmittance (T₀ = T/T₁) of the optical system also the transmittance (T₀) of the analyzer (or analyzer + the additional quarter-wave plate QWP3). Errors were negligible for the quarter-wave plate QWP2 data, so the Jones matrix elements of QWP2 are obtained without the correction.

A polarimetric method was developed for determining the Jones matrix element without the sign ambiguity. The credibility of the method was checked by comparing the theoretical and experimental Jones matrix elements of a quarter-wave plate. The method was used to determine the Jones matrix elements of a twisted nematic liquid crystal panel (TN-LCP) successfully. The proposed method can be used to determine the Jones matrix elements of any other transparent optical materials.