The introduction of the Fiber Optic Gyroscope(FOG) occurred in the late 1970s after the invention of optical fibers. With help received from the researchers in the field of interferometry and telecommunications, The FOG has proven to be a leading technology in various applications for imaging systems, antennas, precise aiming of telescopes, and navigation systems [1-5].

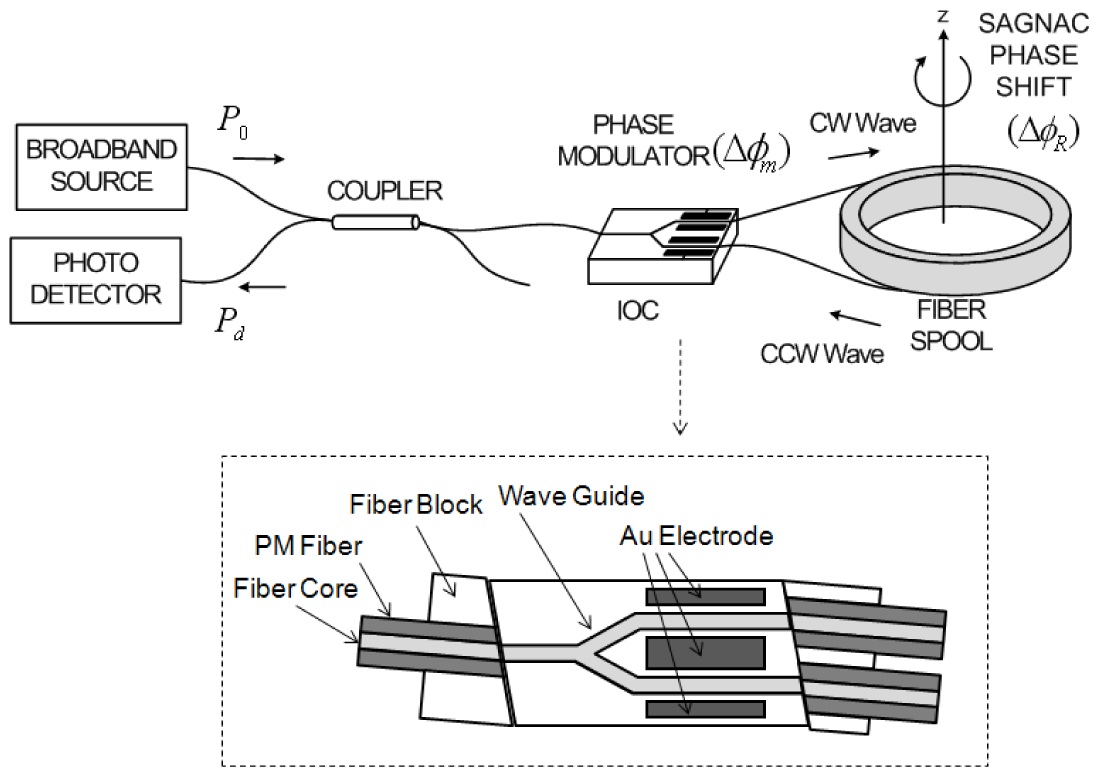
The FOG is a mature technology and was originally designed as a low-cost alternative to the Ring Laser Gyroscope [2-3]. Due to the solid-state optical configuration and fiber technology, the FOG’s performance could lead to 0.001 deg/hr stability in miniature design [4-5]. The main optical components of FOG are composed of fiber, integrated optic chip(IOC), coupler, light source, and detector.

One of the key elements in determining the bias and scale factor of FOG is the modulator’s characteristics in the IOC [6,11-12]. The main function of the IOC is to split the light and to modulate the phases which are combined in a π/2-biased phase for maximum sensitivity, Sagnac phase shift by input rate, and feedback phase for compensating the rate. The important parameters of the IOC for improving the performance of gyroscope are polarization crosstalk, polarization extinction ratio, and modulation amplitude efficiency. Among them, the required level of polarization crosstalk and extinction ratio can be achieved by the manufacturing process.

However, as the modulation amplitude efficiency is intrinsically induced by temperature variation, controlling of the modulation amplitude should be needed because the bias and scale factor are strongly dependent on the feedback element which is directly proportional to the modulation amplitude coefficient of the IOC [7-13]. In addition, the modulation amplitude error can also occur due to the square-wave dither signal which is composed of plus and minus virtual rate. This error can cause bias drift and scale factor error in a closed-loop FOG.

This paper analyzes the temperature dependency of phase modulation amplitude from the effective electro-optic coefficient. In order to investigate how the modulation amplitude error affects the gyroscope, the relationship between temperature dependency of the phase modulation amplitude and the scale factor of the gyroscope is investigated. The error calculation method is improved for the gyroscope with the square-wave dither signal, and implemented on the signal processing module. Some of experimental results with and without the amplitude control loop are also discussed.

The FOG is based on the Sagnac effect, which produces a phase difference proportional to the rotation rate [1]. Light from the broadband source is directed through the first coupler and a single-mode filter to a second coupler included on the IOC. The second coupler divides the light into two parts: one that will propagate clockwise through the sensing coil, and the other that will propagate counter-clockwise. They have opposite phase shift sensitivities to rotation about the coil axis. The Sagnac phase difference between clockwise and counter-clockwise becomes :

where λ is the central wavelength of the light source ; L is the length of fiber ; D is the average loop diameter of the fiber ; Ω is the input rate ; Δ？_R is the Sagnac phase shift ; K_OSF is the optical scale factor of gyroscope.

Figure 1 shows the general configuration of optics and IOC in FOG.

The phase difference induced by input rate is expressed as a cosine relationship for optical power. Once the broadband source generates the power, the photodector output through Sagnac loop in fiber spool P_d is expressed as :

where P₀ is the peak power of the photodetector output.

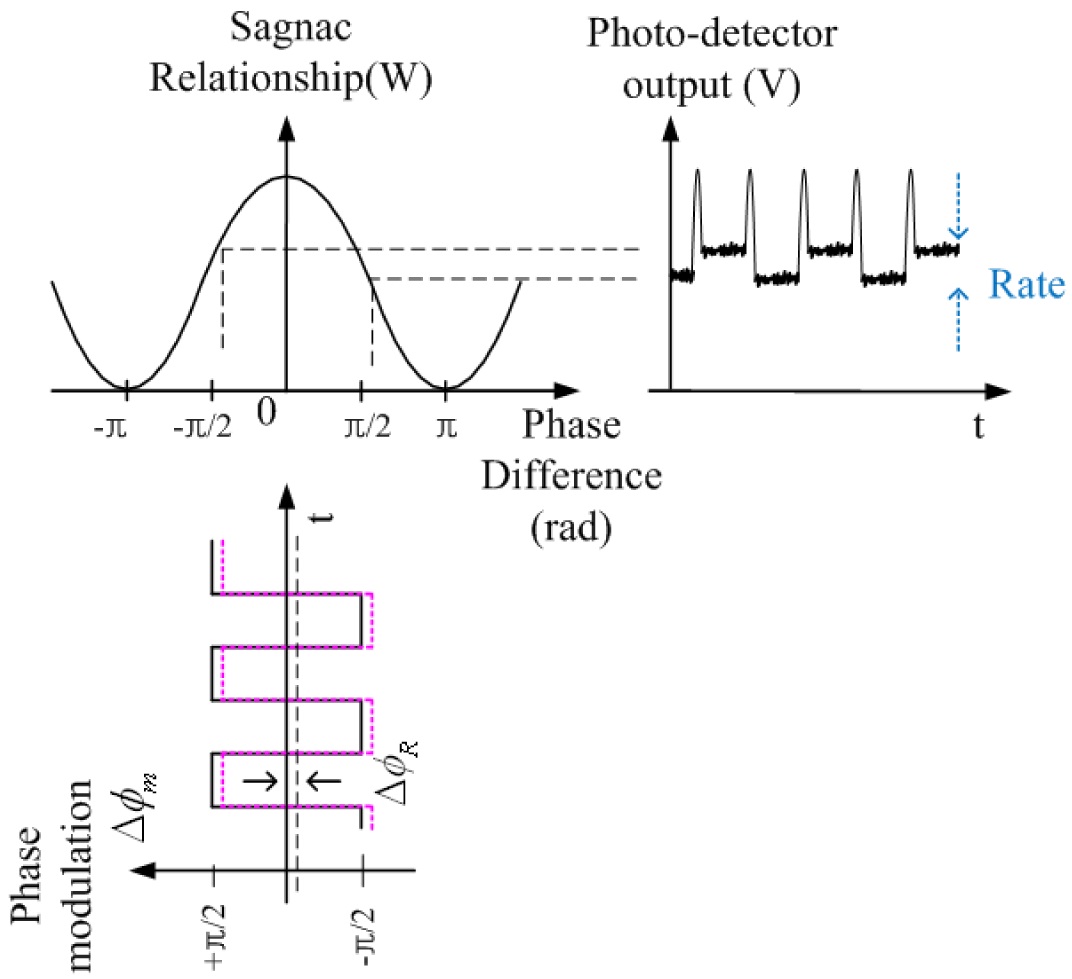
To maximize the sensitivity of the gyroscope, the square-wave modulation-demodulation method is commonly used [12-14]. When the square-wave signal with Δ？_m amplitude is generated, the photodetector output during a period is expressed as :

where Δ？_R is small ; Δ？_m is π/2.

When the square-wave modulation is applied and the input rate occurs, the photodetector output signal is shown in Fig. 2.

If P₀ is 1, P_rate is simply equal to Δ？_R. The equation (5) is only available if both P₀ and Δ？_m are stable. When the phase modulator has a small amplitude error, the equation (5) can be replaced Δ？_m with Δ？_m + δ :

where Δ？_R is small ; Δ？_m is π/2.

From the equation (6), photodetector output has parasitic error due to a nonlinear term cosδ, and can fluctuate due to environmental change. Fig. 3 shows the photodetector output when the phase modulation amplitude error occurs.

In order to reduce the error, the temperature characteristics

of the phase modulator should be analyzed first. The structure of the phase modulator is shown in Fig. 1. The modulator has two electrodes which can double the modulation efficiency. When one electrode of LiNbO₃ is modulated, the phase modulation amplitude becomes [7] :

where γ is the optical confinement factor, defined as the portion of optical mode that is confined in the active layer ; L_m is the modulation length ; Δn is the optical index change in the waveguide active layer.

Assume that the optical wavelength is constantly stabilized by a thermo-electric cooler. The temperature dependency of phase modulation amplitude d(Δ？_m)/dT is proportional to the temperature dependency of the optical index d(Δn)/dT because γ and L_m are relatively small [7-8].

Here, we should look into the optical index change in detail. When the voltage V is applied to the electrodes on the modulator, the optical index change can be expressed as [7]:

where n_eff is the effective optical index of the active layer ; r_eff is the effective electro-optic coefficient; V is the applied voltage ; d is the spatial gap between the electrodes across which the voltage is applied.

From equation (8), the temperature dependency of optical index is composed of n_eff and r_eff. The reports shows that the temperature dependency of r_eff is approximately 4.9×10^-4/℃

and the temperature dependency of n_eff is approximately 4.0~5.0×10^-5/℃ [7-8].

Because the temperature dependency of r_eff is typically ten times higher than the temperature dependency of n_eff, combining equation (7) and (8), the temperature dependency of phase modulation amplitude can be written as :

In this section, the error calculation method from the photodetector output will be derived and an improved method will be suggested. A control loop modeling and the relationship between temperature dependence of phase modulation amplitude and scale factor of a gyroscope will be discussed next.

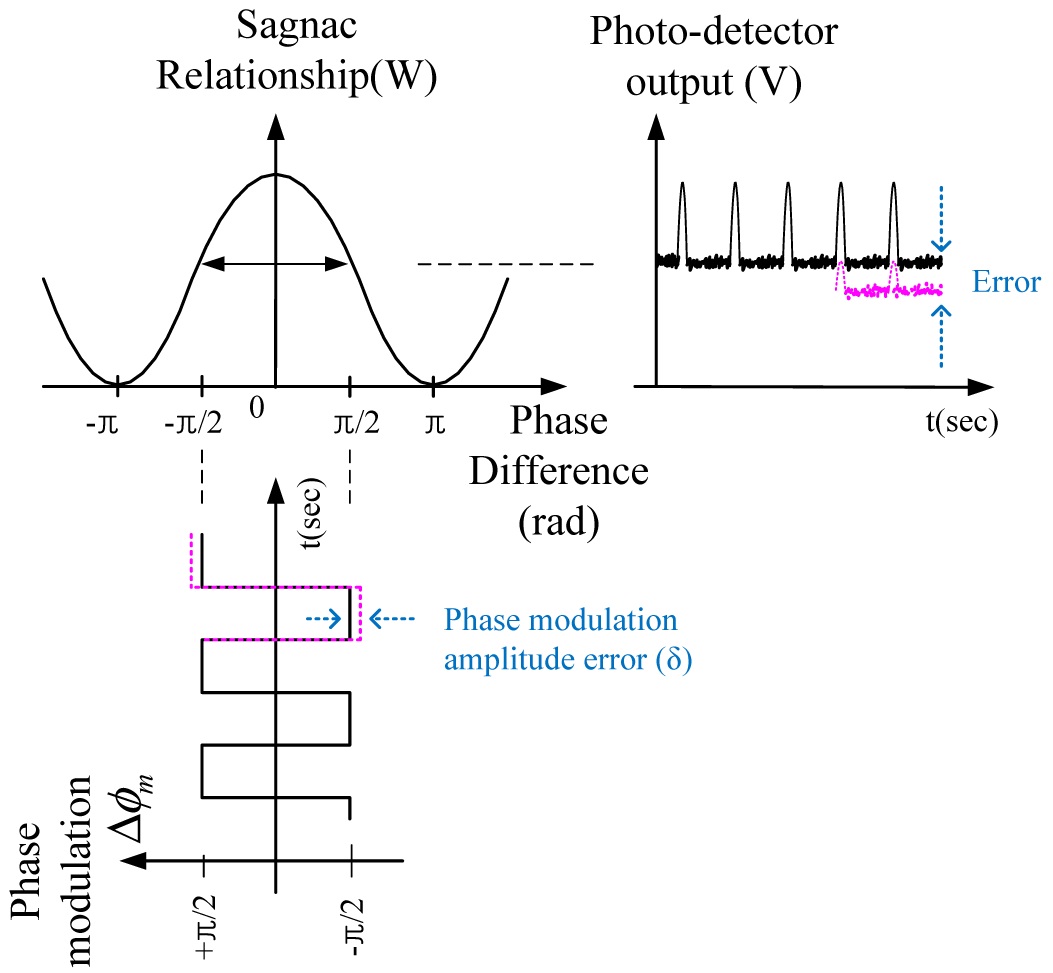
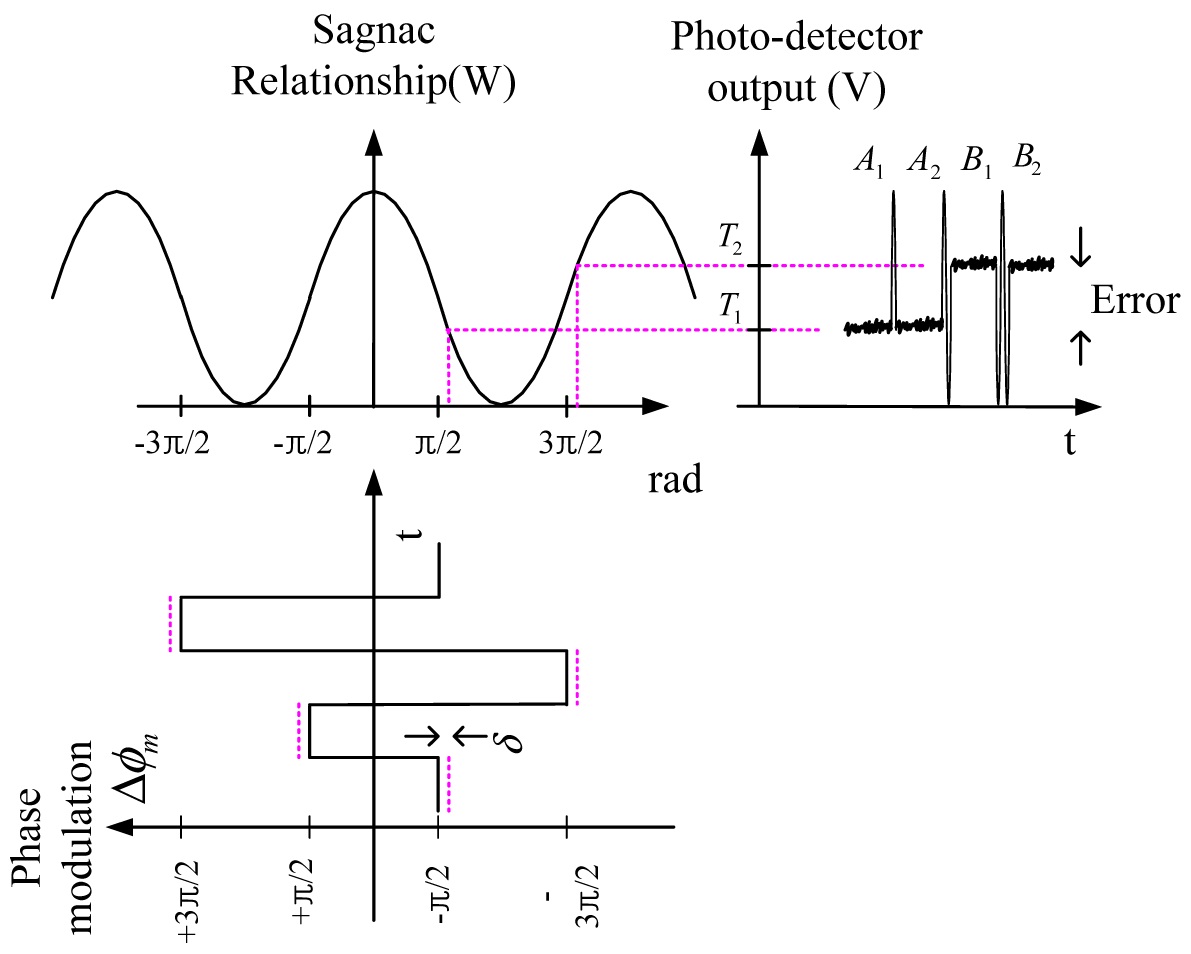
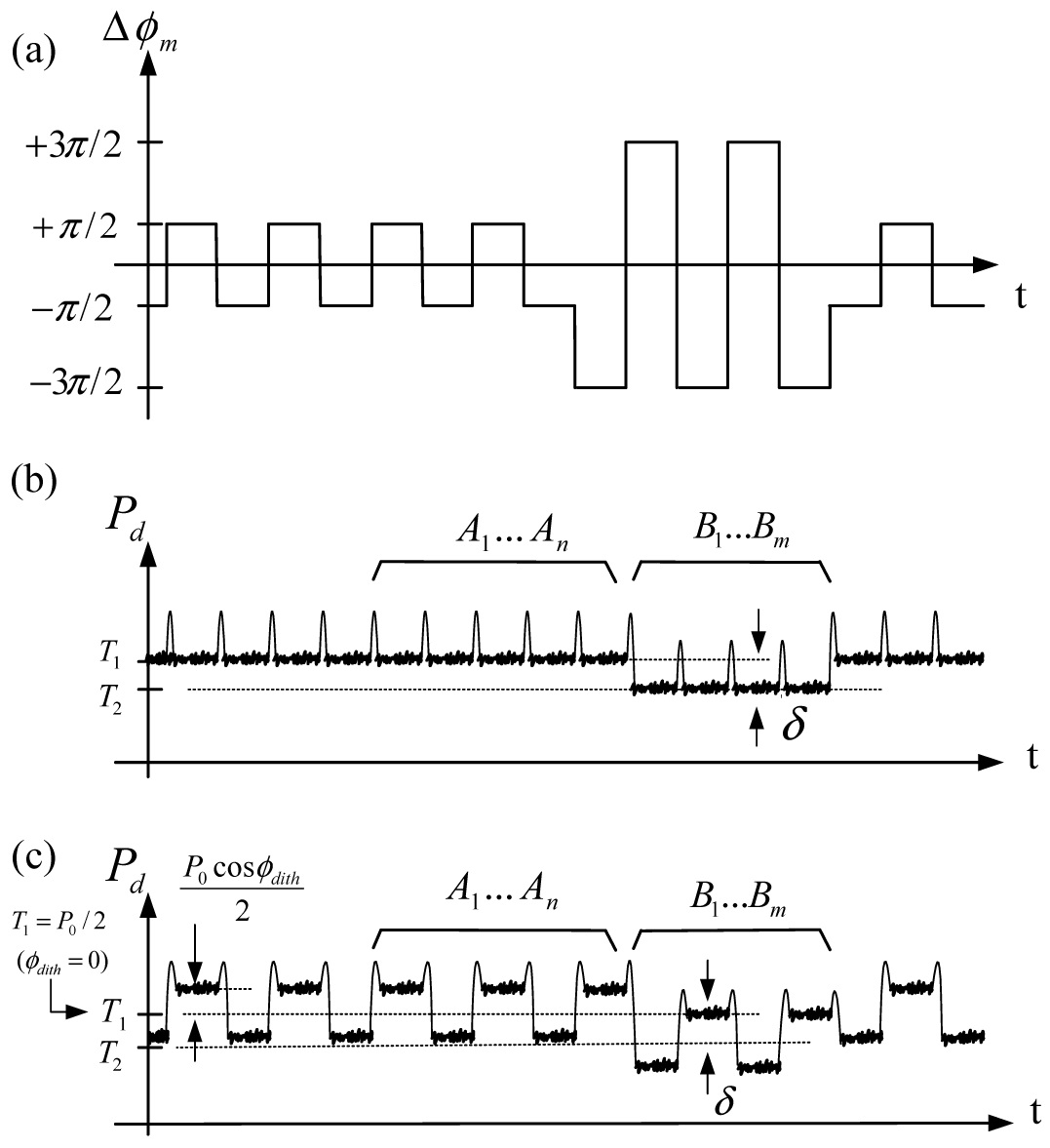
It is impossible to find the phase modulation error from the ±π/2 biasing modulation alone because we don’t know the reference power level of the photodetector output, as shown in Fig. 3. In order to find the phase modulation error, it is necessary to generate additional modulation, ±3 π/2. Fig. 4 shows the photodetector output with both ±π/2 and ±3π/2 modulation.

The modulation steps(pulses) come from the D/A converter through the digital steps determined by the digital register. The closed loop signal processing uses both ±π/2 biasing modulation and ramp modulation. The ramp modulation integrated by input rate digitally is used as feedback phase, which compensate the Sagnac phase proportional to the input rate. Typically, the maximum total steps, combined bias and ramp modulation, are limited to 2π because the maximum output voltage of the D/A converter is set to 2π.

When total steps reach the 2π-limit, the step register is reset, and ±π/2 biasing modulation is changed into ±3π/2 automatically. Considering the modulation amplitude error δ, the photodetector output before and after 2π-reset can be expressed as :

The modulation amplitude error can be expressed by subtracting P₁ from P₂.

In practice, the modulation amplitude error is calculated by the difference between average of ±π/2 steps and average of ±3π/2 steps in order to minimize the noise. The steps can increase or decrease with the input rate value. For a low rate, the steps increase due to a long modulation period that takes long for a small ramp bit to accumulate until 2π. Likewise, the steps decrease in a high rate and vary quickly from ±π/2 steps to ±3π/2 steps. Applying averaging method, the modulation amplitude error can be expressed as :

n : number of photodetector outputs for ±π/2 modulation step

m : number of photodetector outputs during ±3π/2 step

Ai : photodetector output(P1i) for ±π/2 modulation step

Bj : photodetector output(P2j) for ±3π/2 modulation step

This equation is commonly used because it can be simply calculated [13-14]. But in a case of adding a dither signal, equation (13) doesn’t match for exact calculation. Fig. 5 shows the photodetector output with dither signal.

Dithering is a widely used method in gyroscopes to overcome the deadzone where it can’t detect any rate [12-14]. The square-wave dither signal used in FOG changes the photodetector output power because it generates the additional phase shift in feedback modulation. In order to calculate the error considering dither amplitude Δ？_dith, we should apply Δ？_m + Δ？_dith to equation (12), instead of Δ？_m :

This equation has a nonlinear term cosΔ？_dith that should be cancelled or compensated. The modulation amplitude error without dithering (Fig. 5(b)) can be successfully calculated by equation (13) without additional error. But the modulation amplitude error with dithering can include a residual error induced by dither amplitude, Δ？_dith.

The average of photodetector output for even steps B_m results in the same as T₂ because the total average of Δ？_dith is cancelled. But if steps have odd number like A_n, the additional error occurs. Assume that the number of photodetector output A_n is 5 during ±π/2 step as shown in Fig. 5(c). The average is calculated as :

where K is

T₁ is the average of A_n ; T₂ is the average of B_m

In order to remove the above additional error term P₀cosΔ？_dith/10, let’s define S_Δ？m as the sum of photodetector outputs and D_Δ？m as the difference from the first output to sum of following outputs. By subtracting D_Δ？m from S_Δ？m, we can remove the additional error as below :

where n is the odd number ; Δ？_m = π/2.

The variables n, S_Δ？m, and D_Δ？m are known values which can be extracted from the digital logic. The average value T₁ is calculated by simply dividing (2n-2), as shown in Table 1. The same rule for ±3π/2 can be applied.

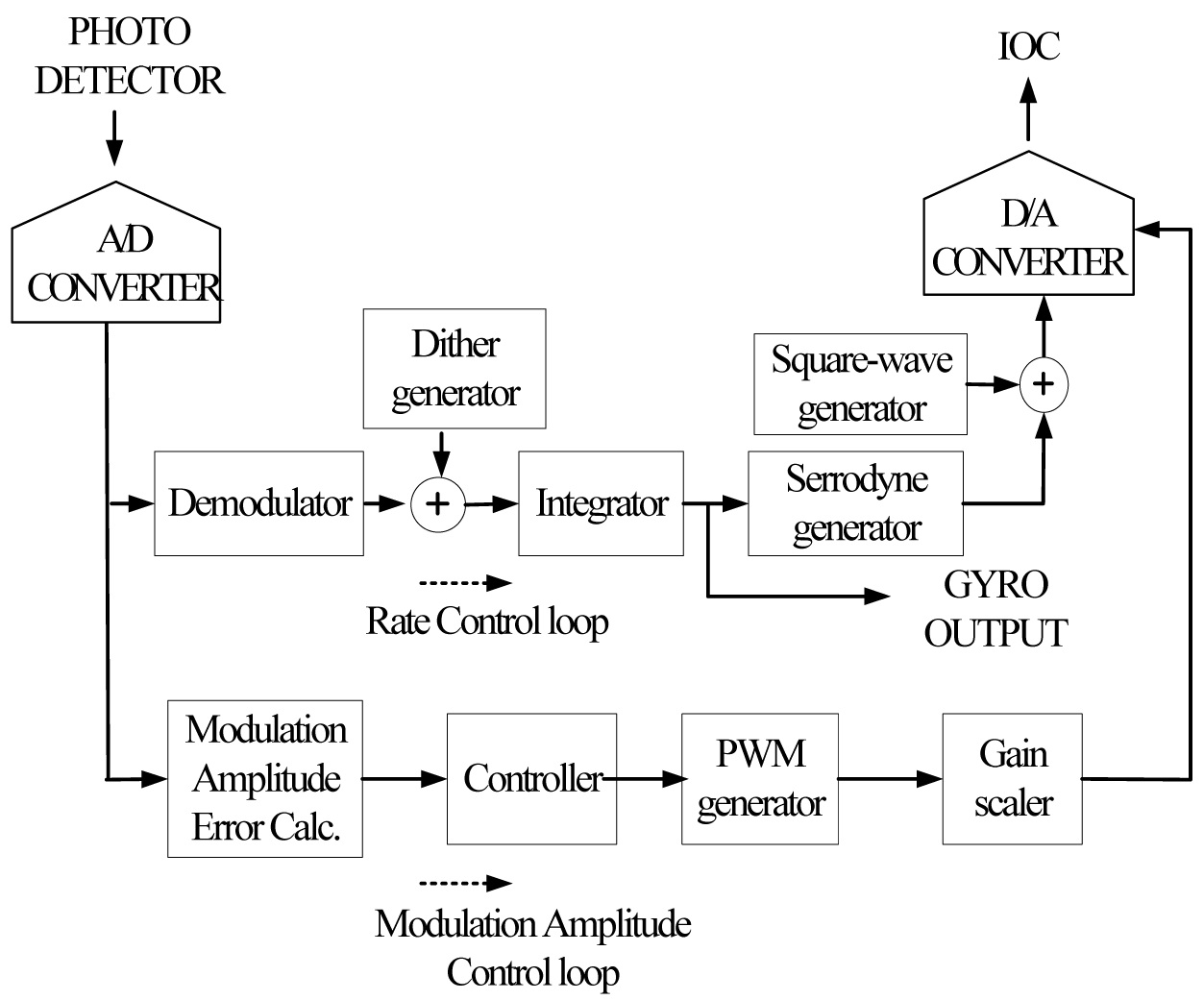
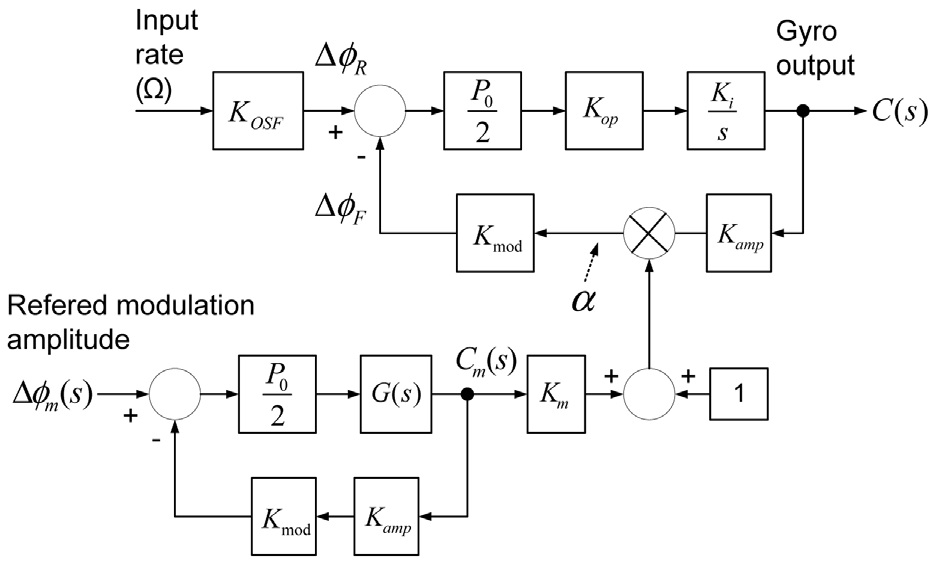
The modulation amplitude error calculated from Table 1 can be compensated by the signal control loop shown in Fig. 6. The modulation amplitude controlled by PWM generator which transforms the digital value to pulse can adjust the range of D/A converter. A control loop model expressed in Laplace transform is shown in Fig. 7.

where K_op is the open loop gain ; K_i is the integrator gain for stabilizing the loop ; K_amp is the gain of the D/A converter ; K_mod is the modulation coefficient ; G(s) is the controller for closing the loop ; K_m is the gain for amplitude compensation.

When the gyroscope operates closed-loop mode in rate, the scale factor is not related to the open loop gain any more if the open loop gain is sufficiently large. The relationship between the control loop transfer function and scale factor can be expressed as :

The scale factor of the gyroscope depends on three factors, K_OSF, K_amp, and K_mod. Among them, the temperature dependency of K_OSF and K_amp can be kept below a few ppm by wavelength stabilization and precision gain reference

i : phase modulation sequences

circuits. So, the temperature dependency of modulation amplitude coefficient dK_mod/dT is dominantly proportional to dn_eff/dT from equation (9), and directly influences the scale factor of the gyroscope.

Assume G(s) has a single-pole integrator. The input-output transfer function for the amplitude control loop is as below :

where τ is the time constant for the loop ; K is the DC gain.

When the loop is closed, the output C_m(s) has a desired value depending on temperature change and the feedback compensation α, shown in Fig. 7, is performed as follows :

The optical head and signal processing modules to verify the effect of amplitude control were implemented on prototype FOG. The optical head was made with Polarization Maintaining (PM) fiber, 1550 nm broadband source, IOC, 2×2 coupler, and photodetector. A 900 m PM fiber with a low birefringence and a small cladding diameter was chosen for good bias performance, wound in fiber spool with quadrupolar winding for reducing the temperature and vibration errors. A broadband source was made with 980 nm-pump laser diode, WDM, and coupler. This configuration promises good stability in power and wavelength. A push-pull modulator with long electrodes on the IOC was designed for high modulation efficiency. A photodetector with low dark noise and low capacitance was chosen for a low noise, high efficiency amplifier design. Special care should be taken in designing the photoamplifier as a small current below a few nano-ampere(nA) corresponding to small input rate can flow on circuits. The signal processing module includes constant current driving circuits for supplying constant power to the laser diode, digital modulation-demodulation logic, control logics for rate and modulation amplitude control, and DSP unit for compensation and digital communication. The optical head and signal processing module are shown in Fig. 8.

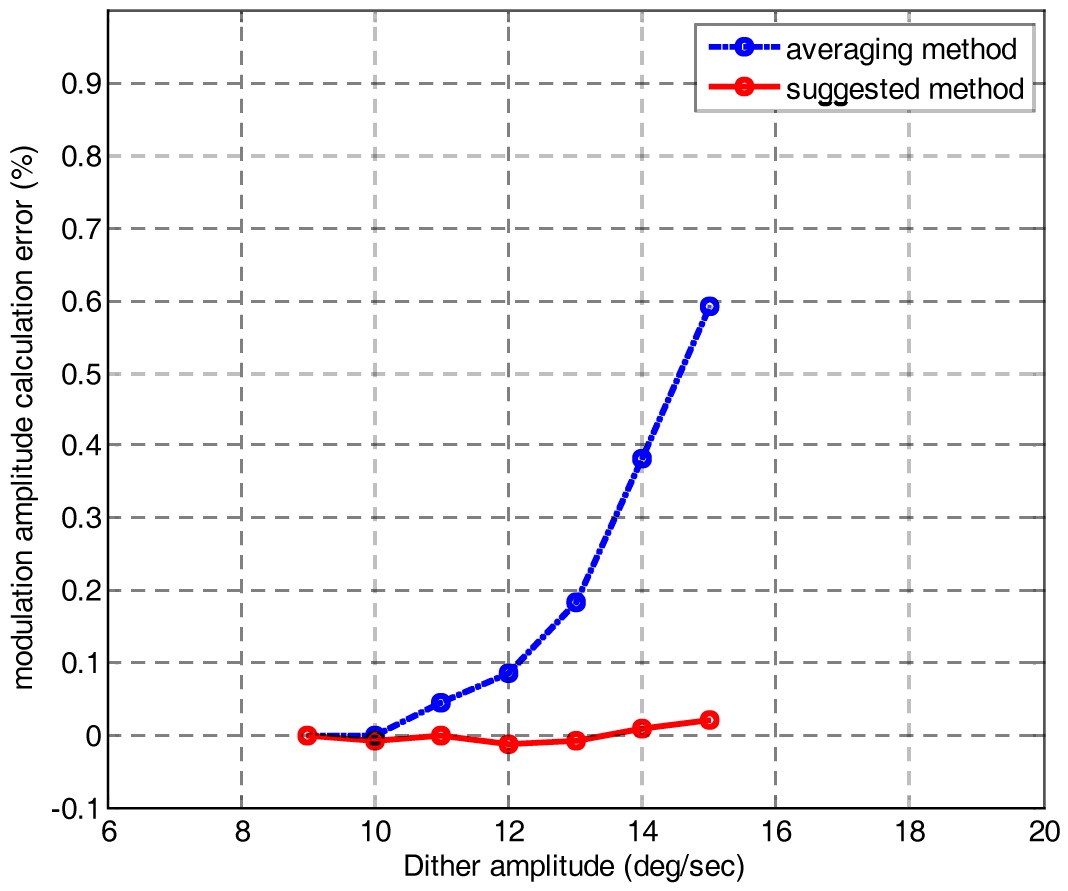
A Figure 9 shows a simulation result which compares a simple averaging method with the suggested method. In an amplitude open-loop mode, the amplitude error was increased up to 0.6% as dither amplitude was changed from 9 deg/sec to 15 deg/sec, while the suggested method was unchanged. This error can lead to a bias drift or scale factor error, even though the error goes to zero in an amplitude closed-loop mode.

On the basis of this simulation result, the suggested method was adopted on signal processing module. Experimental results from Fig. 10 to Fig. 13 show the effect of amplitude

control.

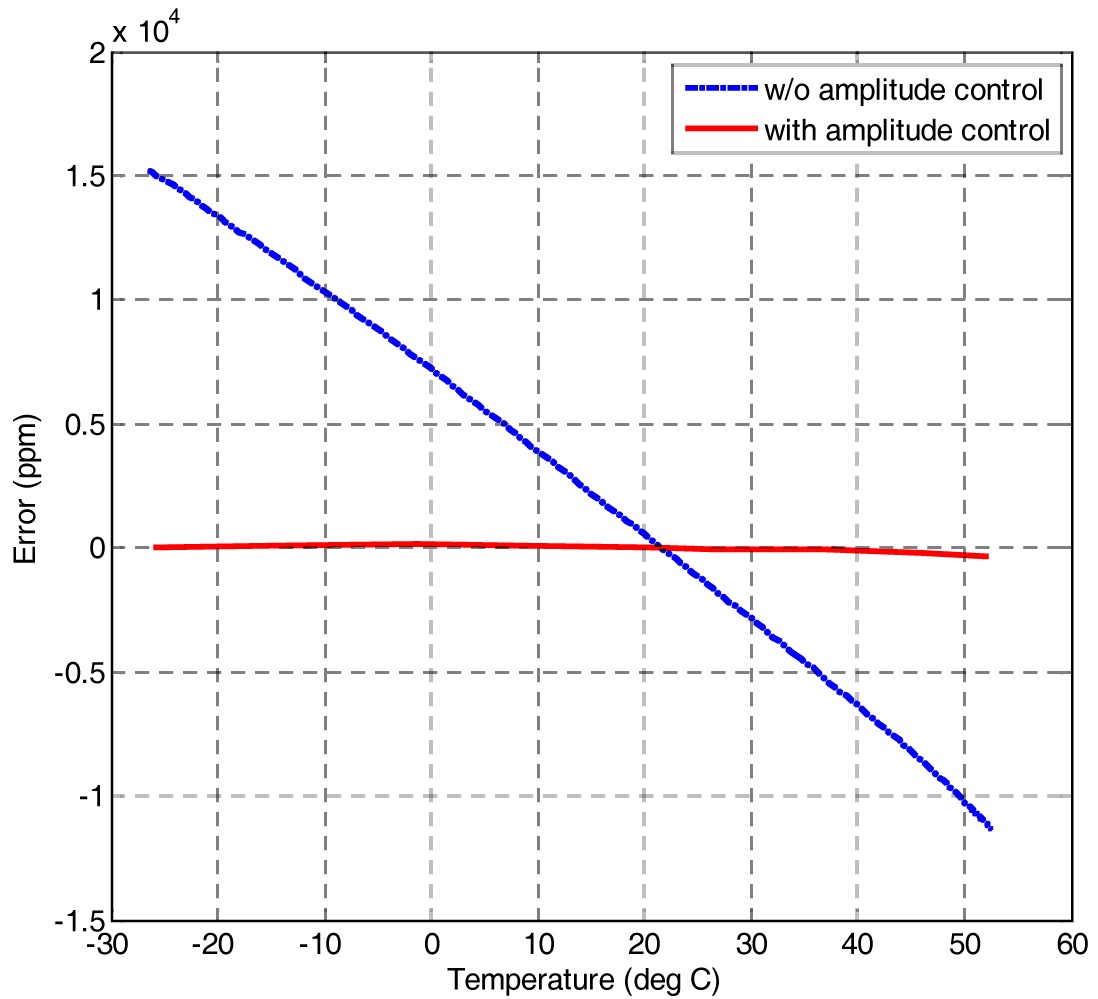
The error without amplitude control shown in Fig. 10 is approximately 26,000 ppm(peak-to-peak) over full temperature range, which corresponds to 325 ppm/℃, a reasonable value for the typical temperature dependency of r_eff as stated earlier in equation (9). Relatively the error with amplitude control is significantly reduced.

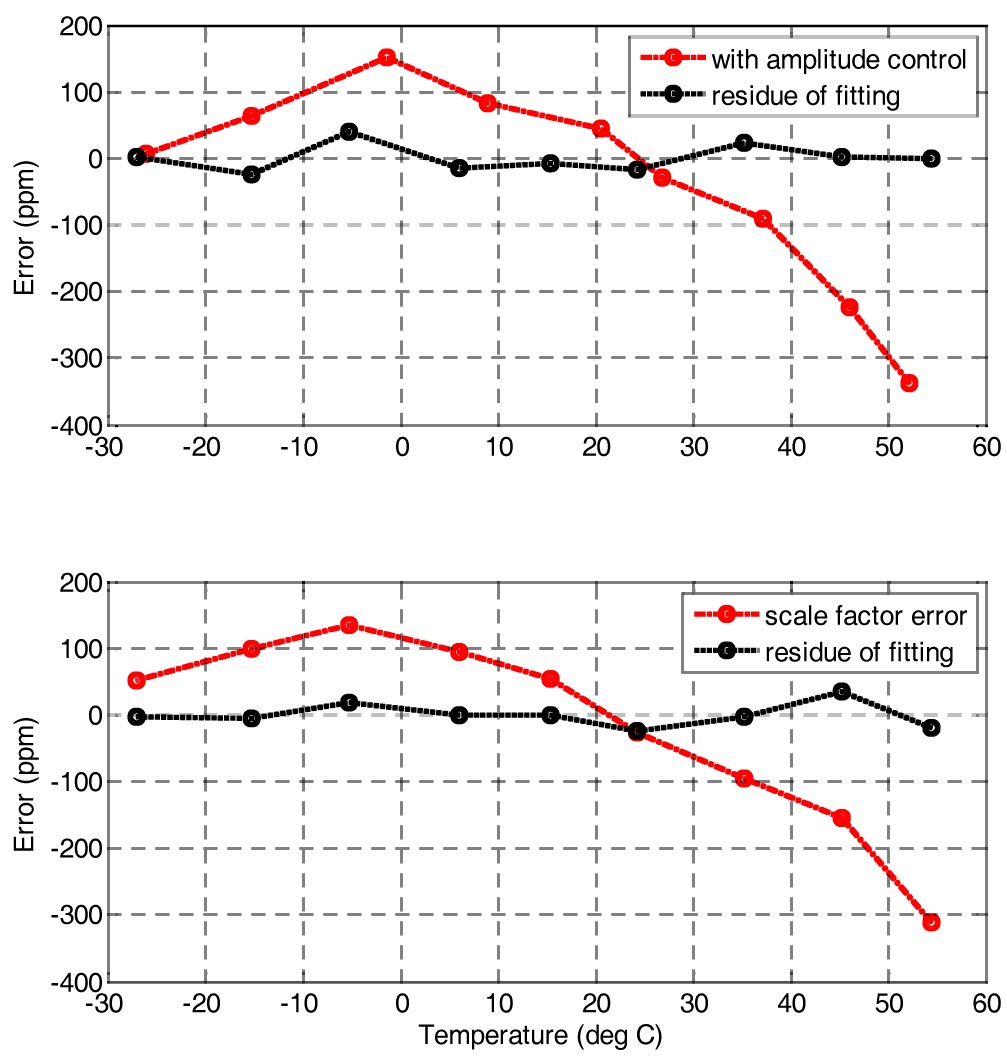
Figure 11 shows the relationship between amplitude control and scale factor. The scale factor is not only related to modulation amplitude K_mod but can be affected by optical scale factor K_OSF, according to equation (17). The variation of K_amp and K_mod can be compensated by amplitude control loop but the variation of K_OSF cannot be controlled. In order to find how much the modulation amplitude error can affect the scale factor, the amplitude control loop was tested without rotation (upper graph) and next, the scale factor was tested in rotation (lower graph). The upper graph residual error when the amplitude is controlled, existing unexpected temperature drift by modulator

or electronics. The lower graph has a similar curve to upper’s and the peak-to-peak values of both errors are almost same, 489 ppm and 444 ppm, respectively, and likewise, the residual errors by third order fitting are 64 ppm and 60 ppm, respectively. This result shows the scale factor is closely related to modulation amplitude. The scale factor residual error also corresponds to a sufficiently low value, acceptable for a navigation system.

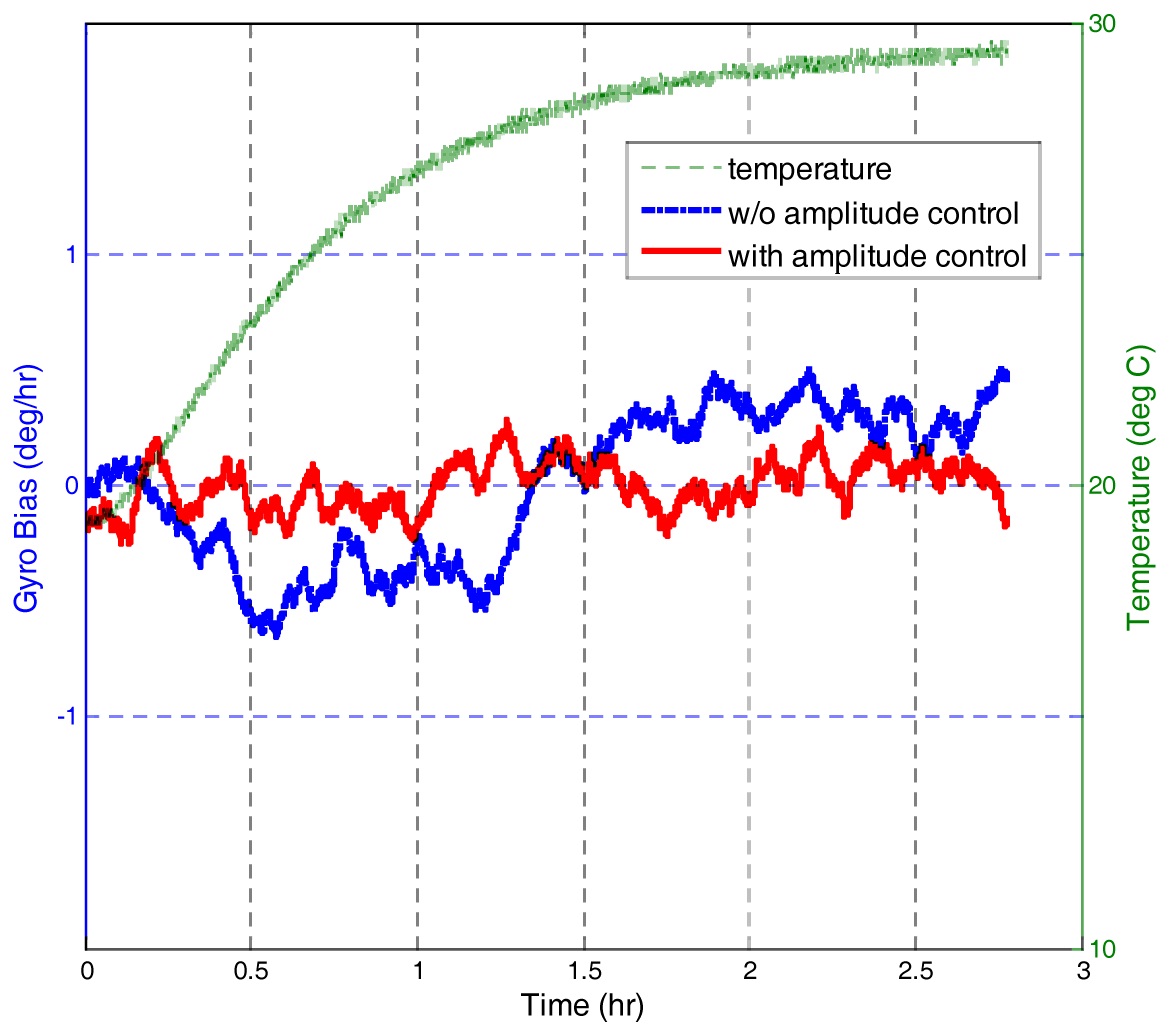
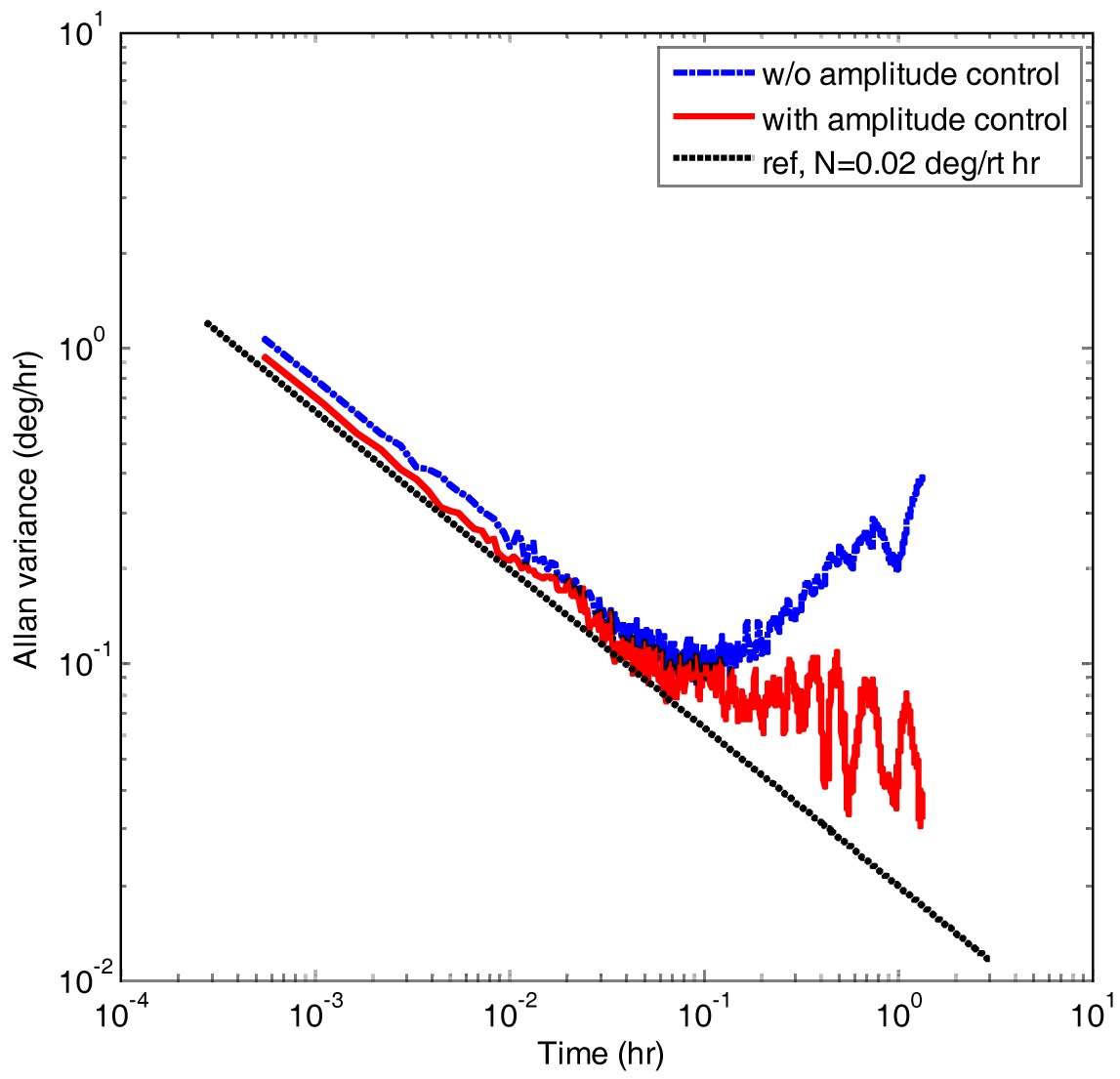
The bias stability, one of the important parameters in determining gyroscope performance, was tested at room temperature. Even in room environment, the temperature is varied approximately 10℃ because the electronics mounted on the inner side of the gyro assembly heats up optical components. In Fig. 12, the bias instability without amplitude control is 0.32 deg/hr (1 sigma), changed along the temperature variation, while it is reduced to 0.1 deg/hr in an amplitude control. The Allan variance in Fig. 13 shows the difference of long-term bias instability more clearly. The Allan variance in an amplitude control is about 0.03 deg/hr, improved three times than without control (The bottom line of datum indicates the Allan variance value)

In this paper, we have discussed the control method of phase modulation amplitude in dithered closed-loop FOG. The origins induced by the modulation amplitude error have been investigated in terms of the effective electro-optic coefficient, pointing out the predominant factor of the scale factor error in gyroscope. The solution to suppressing the modulation amplitude error was proposed, enabling to the exact calculation in a square-wave dithering. We have shown that the control loop effectively eliminated the modulation amplitude error and was successfully implemented on prototype FOG, resulting in improved performances.