This work investigates the orbital perturbations of the cubesats that lie on LEO due to Earth albedo. The motivation for this paper originated in the investigation of the orbital perturbations for closed- Earth pico-satellites due to the sunlight reflected by the Earth (the albedo). Having assumed that the Sun lies on the equator, the albedo irradiance is calculated using a numerical model in which irradiance depends on the geographical latitude, longitude and altitude of the satellite. However, in the present work the longitude dependency is disregarded. Albedo force and acceleration components are formulated using a detailed model in a geocentric equatorial system in which the Earth is an oblate spheroid. Lagrange planetary equations in its Gaussian form are used to analyze the orbital changes when e≠0 and i≠0 . Based on the Earth’s reflectivity data measured by NASA Total Ozone Mapping Spectrometer (TOMS project), the orbital perturbations are calculated for some cubesats. The outcome of the numerical test shows that the albedo force has a significant contribution on the orbital perturbations of the pico-satellite which can affect the satellite life time.
Recently, there is significant interest in developing a new class of standardized pico-satellites called cubesats. Cubesats have been the best choice for universities and research institutes toward starting space technology developments. The mass of the cubesat is restricted to be 1 kg and its size is confined to be .1 m on all sides. This small size is considered as the main advantage of cubesats which enable them to be launched as an auxiliary payload and result in less cost and test requirements. The surface of the cubesat is covered by six aluminum plates, each of which has a solar chip attached to it. The majority of these satellites are placed in a low Earth sun synchronous orbit (the inclination is close to 98°) [1] and [11].
Many factors affect the satellite orbital motion. The Earth gravitational field has the master role in perturbing the satellite dynamical motion. However, the non-gravitational factors (e.g. solar radiation pressure, air drag, luni-solar attraction… etc) play a significant role in perturbing the orbital motion. Several authors have performed a suite of studies and models to illustrate those effects on various types of satellites and orbits. Over the last few years, a vast knowledge of natural radiation pressure effects on satellite dynamics and rotation has been achieved. The main contribution of the natural radiation pressure is due to the direct solar radiation so a variety of models were constructed to estimate their force [2], [3], [9], [11], and [19]. The second main contribution of radiation forces is due to the Earth reflected radiation known as the albedo. It is an extremely complex phenomenon which shows relevant spatial and temporal variations. Albedo depends upon the reflectivity of the illuminated surface of the Earth that is visible to the spacecraft, the solar angle, and the position of the spacecraft in space. Moreover, it depends on seasonal variations and geographical longitude and latitude of the Earth surface that is illuminated by the Sun and seen by the satellite [4], [6] and [17].
Based on a new numerical modeling of the albedo in which the irradiance is calculated depending on the geographical latitude, longitude and altitude of the satellite, the main issue of this work is to investigate the orbital perturbations of the cubesats lying on LEO due to Earth albedo.
The albedo irradiance, which reaches the satellite surface, is determined using a numerical model. This model is based on partitioning the Earth surface into a number of cells forming a grid. Then the incident solar irradiance on each cell is used to calculate the total radiant flux. The total albedo irradiance,
where
is the unit vector normal to the grid cell and ρ
where Δθ
It was obvious that the albedo irradiance had a large dependency on the geographical latitude of the grid points. The maximum albedo is observed over the poles and decreased by moving away from them and towards the shadow side of the Earth. Moreover, there is a significant dependency on the longitude and the solar angle, where albedo has maximum values for low solar angles [6], [16] and [17]. However, as previously mentioned, the longitude dependency is disregarded in this work.
These equations represent the albedo contribution of a single Earth cell. However, the sunlit area visible to the satellite is decomposed into a definite number of cells. So, the total albedo irradiance reaching to the satellite can be obtained by summing up the contribution of each cell [6] and [17]:
where
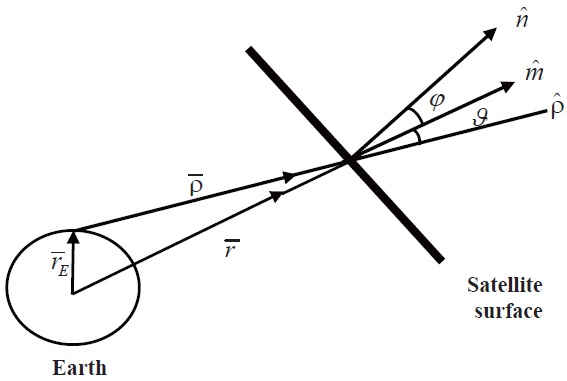
The total radiant force exerted on a flat non-perfectly reflecting surface is given by [13]:
where,
where
is a unit vector directed the force direction,
For non-perfectly reflecting surfaces, the force vector,
, is not directed normal to the surface. But, it inclines by an angle
The geocentric equatorial system with
, is given by:
where
is the satellite position vector and
is the Earth radius vector. For oblate Earth, the Earth radius vector is given by [7]:
with
where
The satellite position vector,
, in the geocentric coordinate system, is given by [7]:
with
where Ω is the longitude of the ascending node,
with
The acceleration experienced by a satellite of mass
The radial components of the disturbing accelerations,
is given by:
The tangential component of disturbing acceleration is given by:
where
is a unit vector in the direction of the angular momentum vector. It can be expressed as [7]:
The perpendicular component of disturbing acceleration is given by:
It is worth noting that the spacecraft is decomposed into a finite number of small elementary surfaces. Consequently, the total force acting on the cubesat is considered to be the sum of all forces acting on each elementary surface [3], [10] and [14]. At a given time, the total radiant acceleration affecting the spacecraft is
where k is the number of satellite surfaces and
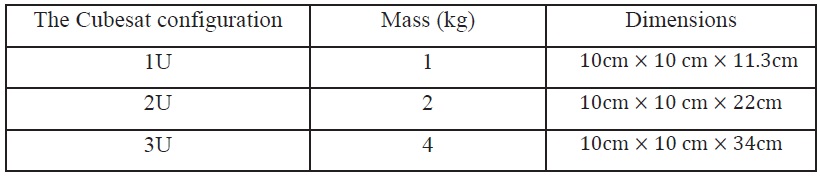
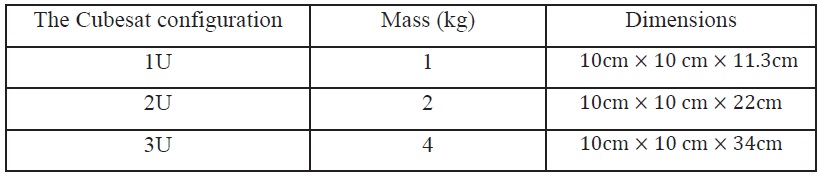
The Cubesat is a cube shaped picosatellite constrained to CalPoly’s specifications. The structure of these cubesats may be consisted of one cube “1U”, two cubes “2U” or three cubes “3U” as specified in table 1 [5] and [12].
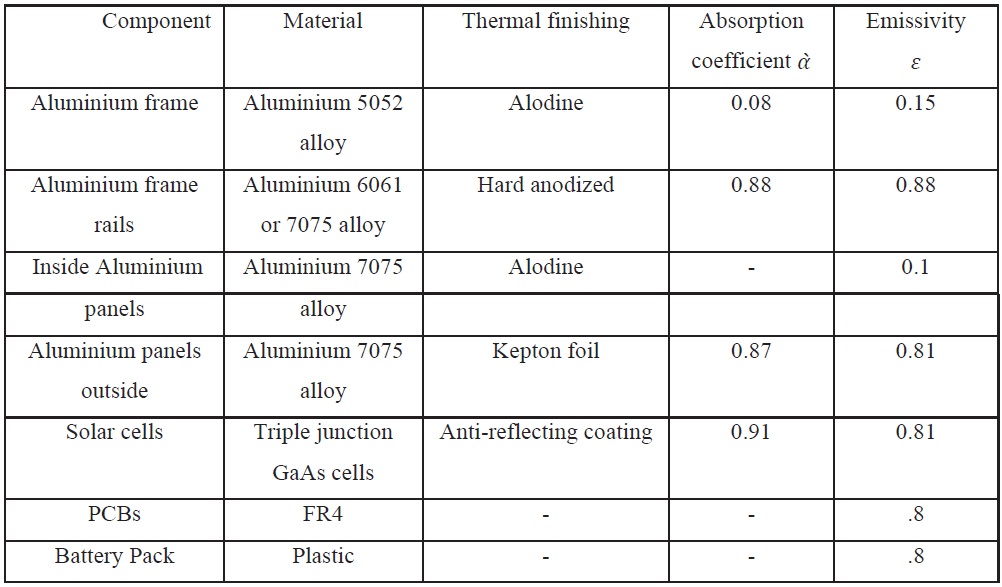
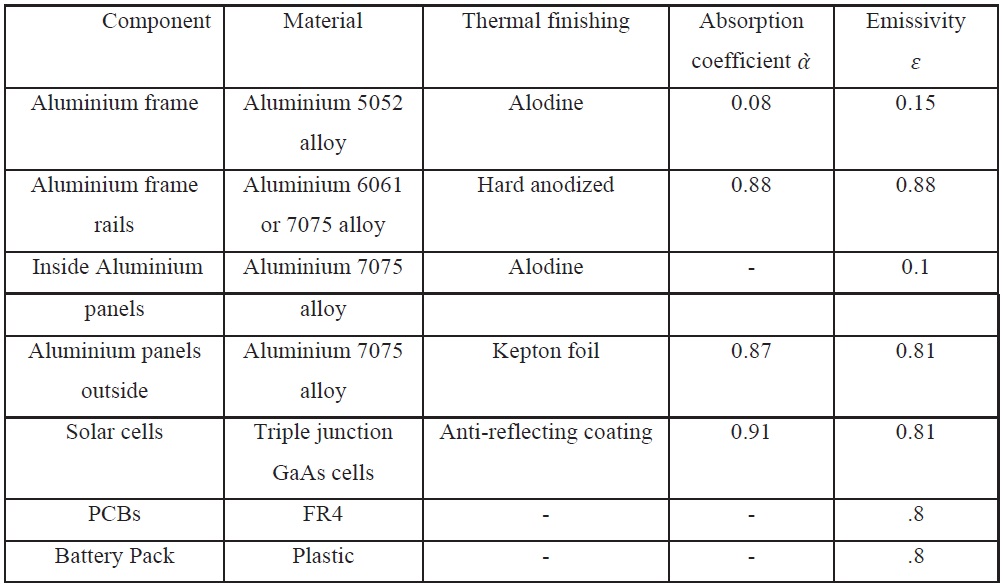
The cubesat’s thermo-optical properties are also constrained to CalPoly's specifications as tabulated in table2 [5] and [12]:
Based on Eqs. 15, 17 and 18 and make use of the thermooptical properties and area to mass ratio of cubesats, the acceleration components experienced by a cubesat are given by the following equations:
[Table 1.] Area and mass of 1U and 3U cubesats
Area and mass of 1U and 3U cubesats
[Table 2.] Main characteristics of the cubesat external structure
Main characteristics of the cubesat external structure
On account of the different area to mass ration of each cubesat, the constant
>
Perturbations of the orbital elements
For orbits of
The variation of
where
is the mean motion. The perturbation equations are obtained as functions of the acceleration components
as the following [18]:
where E is the eccentric anomaly.
Albedo force affecting on LEO cubesats of different perigee heights and area to mass ratio for one satellite revolution
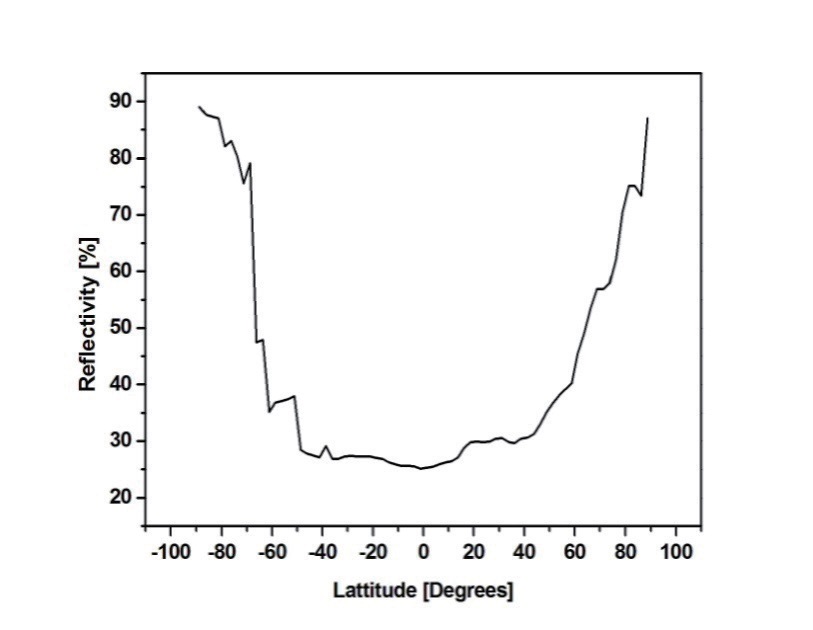
Having implemented the Earth’s reflectivity data measured by NASA’s Earth Probe satellite, which is part of the TOMS project (Total Ozone Mapping Spectrometer) [15], the Earth’s reflectivity as a function of latitudes is illustrated in fig. 2.
As illustrated in Fig. 2, the albedo has a maximum value of ~ 88 % over the latitude of 88.75 South (close to the South Pole). However, it has a minimum value of ~ 13.8 % over the latitude of 1.25 South (close to the equator).
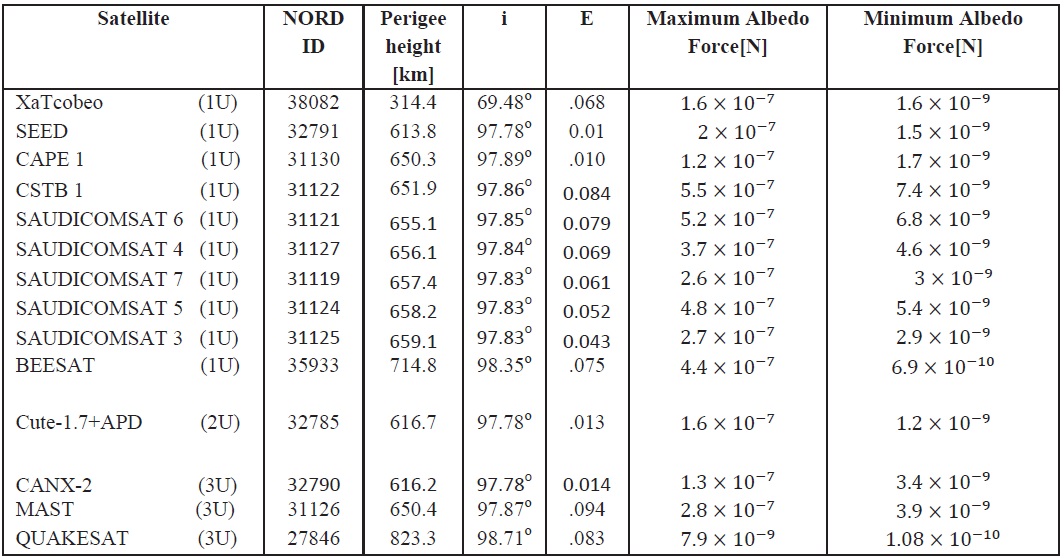
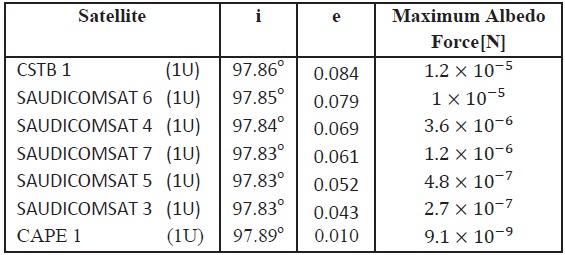
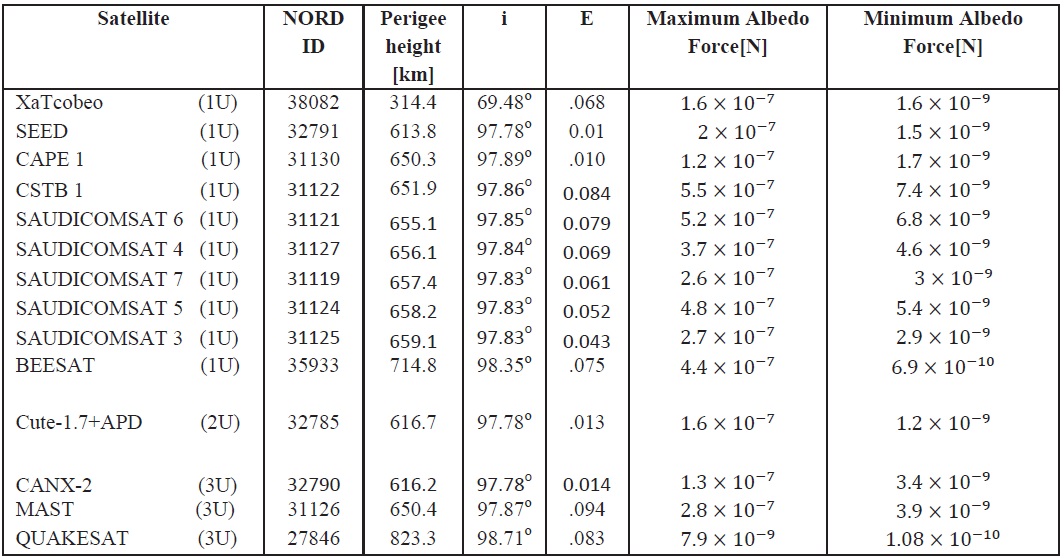
In the present work, the albedo force is calculated for some LEO cubesats of different configuration and perigee heights. The results are tabulated in the following table:
As illustrated in table 1, the maximum albedo force is in the order of ~ 10-7 N and the minimum value is in the order of ~ 10-10 N which is experienced by a cubesat of ~ 823 perigee
height.
The dependency of the albedo force on the orbital eccentricity is studied. Some cubesats are chosen approximately for the same inclination and different eccentricities and arranged in ascending order according
[Table 4.] Dependency of albedo force on the orbit eccentricity
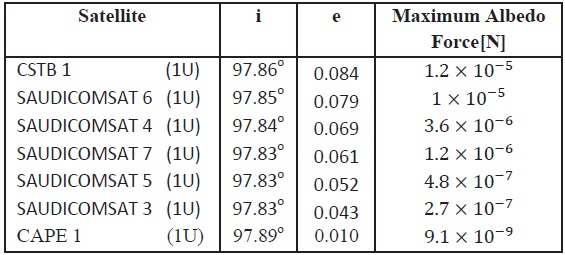
Dependency of albedo force on the orbit eccentricity

Mean orbital perturbations of some LEO cubesats due to albedo effects over one satellite revolution
to their eccentricities. The results showed that albedo force depends directly on the orbital eccentricity as seen in table 2.
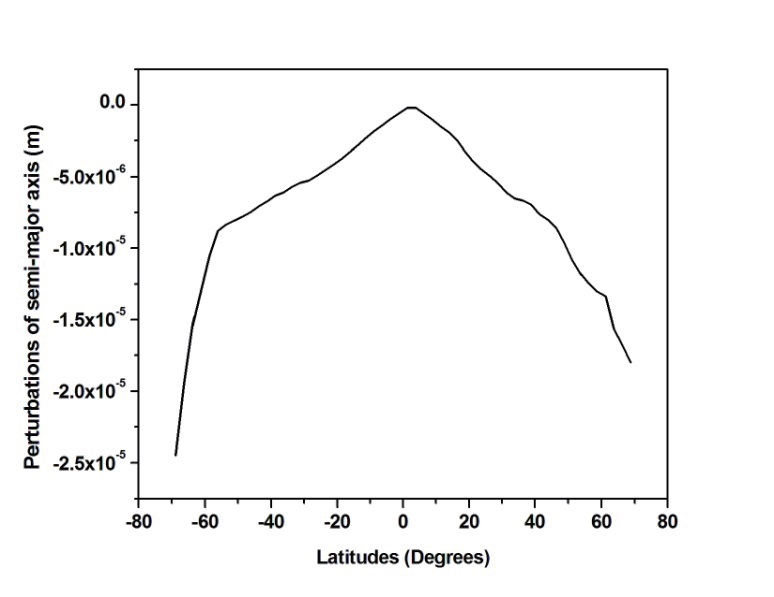
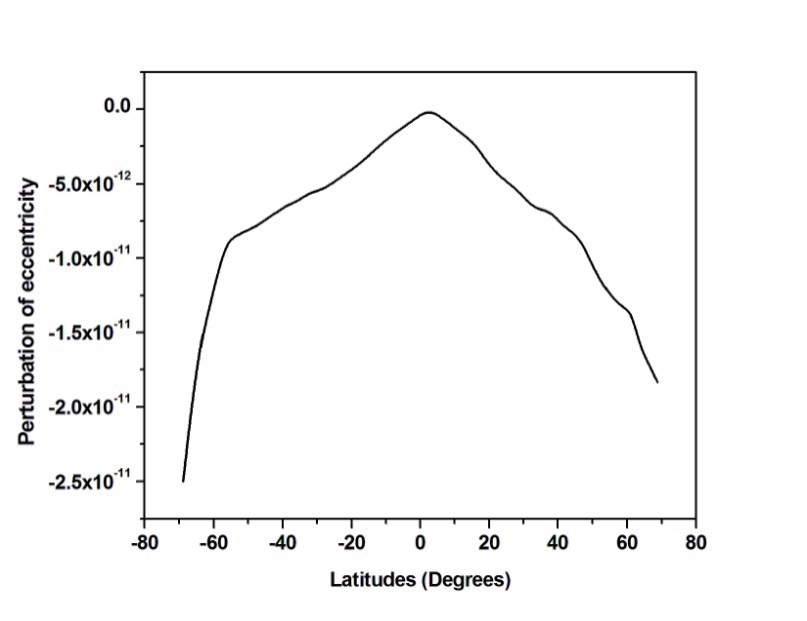
The mean orbital perturbations of the orbital elements are studied and illustrated in table 3.
Based on the tabulated results in table 3, the maximum perturbations of the semi-major axis, eccentricity and argument of perigee are in the order of ~10-4, 10-10 and 10-9, respectively. However, the minimum values are in the order of ~10-6, 10-12 and 10-11, respectively.
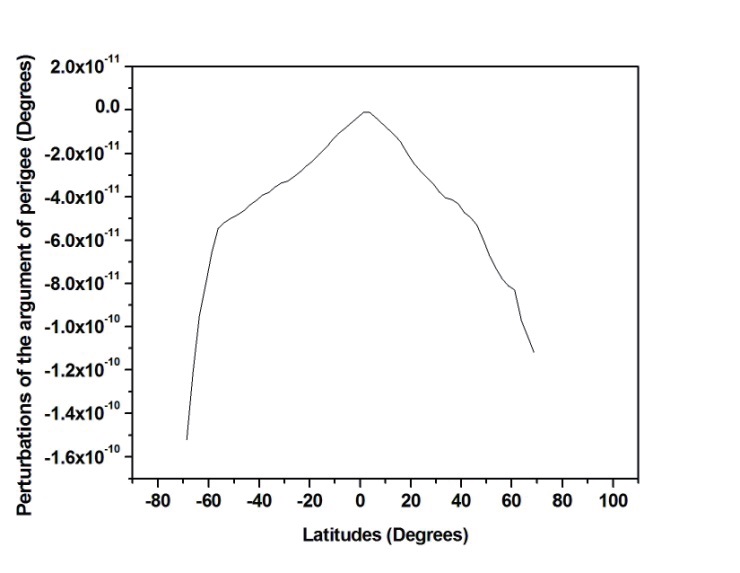
The perturbations of the semi-major axis, eccentricity and argument of perigee of the satellite XaTcobeo are illustrated in details over one revolution in the following figs 3-5:
As illustrated previous figures, the maximum albedo perturbations for the semi-major axis, eccentricity and argument of perigee were experienced by the satellite when
it passes close to the Earths poles where the Earth’s reflected radiation has its maximum percentage. However, the minimum perturbations occurred when the satellite passes close to the Earths equator.
A simple analytical model of the terrestrial albedo force was constructed w.r.t. the geocentric equatorial coordinate system in which the Earth was considered as an oblate spheroid.
The current numerical test has validated that the albedo force has significant contribution on the satellite dynamics and also a great dependency on the geodetic latitudes which depends on the satellite field of view. The maximum albedo force is in the order of ~ 10-7 N. Nevertheless, the minimum value is in the order of ~ 10-10 N.
The results show that the maximum perturbations of the semi-major axis, eccentricity and argument of perigee are in the order of 10-4, 10-10 and 10-9, respectively. However, the minimum values are in the order of 10-6, 10-12 and 10-11, respectively. Therefore, we can conclude that the effects of the albedo have a considerable disturbance on the orbit and it can affect the cubesats life time.
In our future work, the Sun’s apparent path (the ecliptic) in the theoretical modelling and application will be considered. Moreover, the dependency of the albedo intensity on the Earth’s longitude is to be investigated.