For optimal formation reconfigurations of satellites in space, various analytical and numerical methods have been developed so far. Carter and Pardis analyzed for the optimal thrust which had the upper and lower limit (Carter & Pardis 1996). Palmer presented an analytic solution for the optimal reconfiguration problem based on the Fourier series expansion of thrust (Palmer 2006). Cho & Park derived a simple analytic solution for linear dynamics in the local vertical, local horizontal frame (Cho & Park 2009). Lee and Park derived approximated analytical solutions considering nonlinearities of the terrestrial gravity, eccentricities of a chief satellite, and J2 effects by perturbing the solution to the linear Hill equation (Lee & Park 2011). These analytical methods generally provide solutions based on the linear dynamics, which are limited to describe the actual dynamic environments precisely. While numerical methods can be employed to yield a precise solution based on nonlinear dynamics, it usually requires initial guess and iterative process for obtaining the initial costate vector accurately.

Recently, Guibout & Scheeres formulated a formation reconfiguration problem near the L₂ Lagrangian point of the Hill three-body dynamics as a Two Point Boundary Value Problem (TPBVP) of the Hamiltonian dynamics, and presented a new solution procedure without initial guess and iterative process of determining the initial momenta by using generating functions appearing in the Hamilton-Jabobi Theory (Guibout & Scheeres 2004). Since then, the generating function approach has been considered as an appropriate tool for reconfiguring formation flying satellites which usually needs to consider varying boundary conditions and time spans for a number of satellites (Guibout & Scheeres 2006). Moreover, Park et al. extended the generating function approach to an optimal control problem, and presented a solution by obtaining the initial costate vector for truncated nonlinear dynamics (Park et al. 2006).

In this paper, Park et al.’s nonlinear optimal control method with generating functions is applied to the optimal reconfiguration problem on the Projected Circular Orbit (PCO) to analyze the performance of the generating function approach comprehensively. The analysis is conducted on the convergence of trajectories and performance index to those of a nonlinear reference solution obtained from a numerical shooting method. The performance index analyses also exhibit some insightful characteristics by varying PCO configuration parameters under nonlinear dynamics.

An optimal reconfiguration problem for satellites flying in formation can be formulated as an optimal rendezvous problem, and can be mathematically framed as follows: minimize the performance index

subject to nonlinear dynamic equations in affine form with initial and final boundary conditions

where x ∈ R^n×1 and u ∈ R^m×1 are the state and control vectors, respectively. The above optimal reconfiguration problem has the following first order necessary conditions by applying the Pontryagin Principle (Kirk 1970):

λ is the costate vector, and the subscripts on the bottom of Eqs. (4) and (5) indicate partial derivatives. When Eq. (6) is substituted into Eqs. (3)-(5), the optimal reconfiguration problem is expressed as a TPBVP for a standard Hamiltonian System.

Once the initial costate vector λ₀ is obtained, this TPBVP is transformed into an Initial Value Problem (IVP), and the solution for optimal reconfiguration is obtained through a simple forward integration. When the dynamic system is nonlinear, many numerical methods can be used for obtaining the initial costate vector. However, it requires initial guess and iterative procedure for determining the initial costate vector, which may cause computational burdens to design optimal reconfiguration trajectories for various boundary conditions and time spans of formation flying.

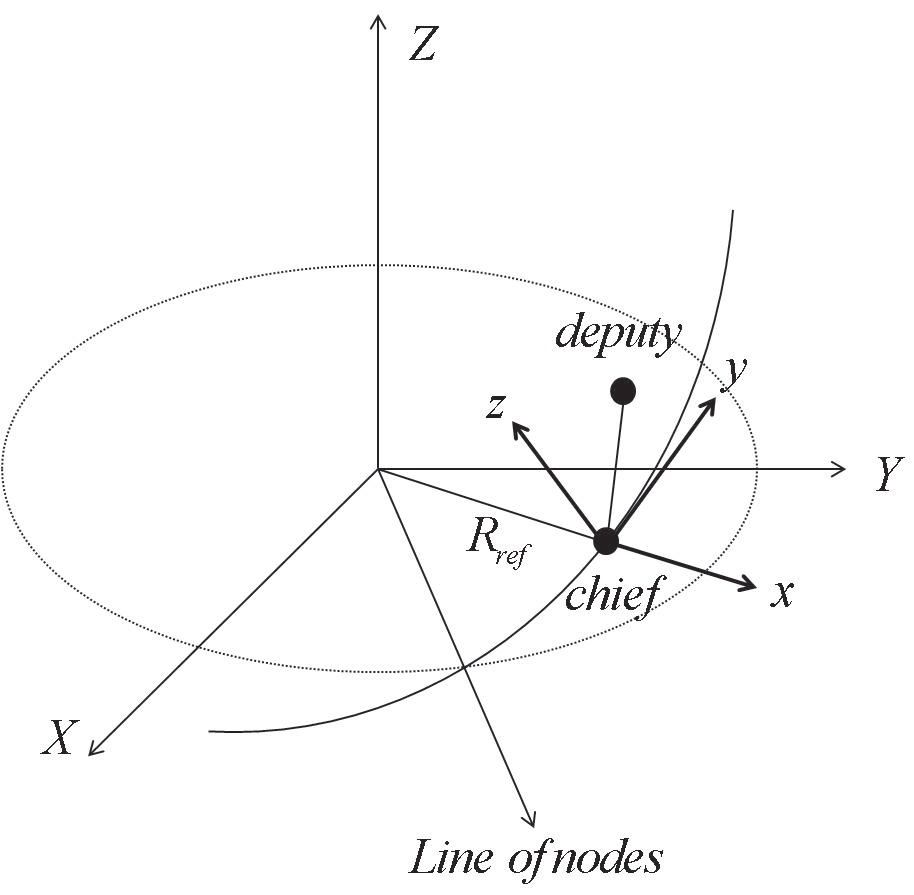
The nonlinear relative motion for optimal reconfiguration problems is expressed in the RSW coordinate system as shown in Fig. 1. The frame XYZ represents the Earth-Centered Inertial (ECI) frame with the center of the earth as the origin, where X directs to the vernal equinox, Y is in the 90° direction to the east from the vernal equinox on the equatorial plane, and Z completes the right hand coordinate system. In the relative RSW coordinate system with its origin located at the reference chief satellite, x is in the opposite direction to the center of the earth, z is perpendicular to the reference orbital plane, and y completes the right hand coordinate system. The distance from the center of the earth to the deputy satellite is expressed as R with the unit vectors

in the RSW coordinate system as follows.

R_ref is the radius of the reference orbit, which is assumed to be circular in this paper. Eq. (8) is differentiated twice with respect to time to obtain the acceleration of the deputy:

ω is the angular rate of the reference orbit. Assuming that the deputy is only influenced by the central gravity of the

earth, the relative dynamic motion of the deputy with respect to the chief in the RSW coordinate system is stated as

where R is the magnitude of R . Eq. (10) is normalized by R_ref and the reciprocal of ω, and is expressed in the state space form as follows.

Here, [x₁ x₂ x₃]^T is the position vector in the RSW coordinate system, and [x₄ x₅ x₆]^T is the associated velocity vector.

Now the optimal control method using the generating function is briefly summarized and applied to the optimal reconfiguration examples. The details regarding the generating function and the Hamiltonian system are given in Park et al. (2006) and Greenwood (1977). First, define another trivial Hamiltonian system for constant flows of initial state and costate vector as

where K represents the constant Hamiltonian of this system, and is set to be zero without loss of generality. Generating functions define canonical transformations between two different Hamiltonian systems, and thus provide the relationship between the Hamiltonian systems, Eqs. (7) and (14), as follows.

Theoretically, 2ⁿ kinds of generating functions can exist by the assignment of independent variables. Here two out of 4 principal kinds of generating functions are mainly used:

Each generating function satisfies the following relationships:

When the associated Hamilton-Jacobi equation, Eq. (17), is solved for the F₁ generating function, the initial costate vector is obtained by the relation λ₀=－∂F₁/∂x₀ in Eq. (18). However, it must be noted that the F₁ possesses a fundamental singularity, since the pair (X, X₀), which is set to be independent variables, loses their independence when t=t₀. In order to avoid this singularity, the Hamilton-Jacobi Equation is solved for the F₂ generating function, which is then transformed into the F₁ by the Legendre transformation which algebraically connects generating functions of different types.

In order to solve the Hamilton-Jacobi equation, the Hamiltonian is first expanded as a Taylor series with respect to a nominal solution as follows:

Here, △ is the increment from the nominal solution. If the nominal solution is simply 0, Eq. (19) can be expressed without △ for simplicity:

Next, the F₂ is expanded as a Taylor series with respect to the independent variables x and λ₀ :

The maximum order of the F₂-expansion is set to be the same as that of the Hamiltonian expansion. Since the control vector is obtained from partial derivatives of the generating function by Eqs. (6) and (18), the order of the optimal solution is k－1 when the order of the generating function is k. Obviously, higher k reflects higher degrees of nonlinearity. By substituting the relation of λ₀=－∂F₂/∂x into Eq. (20), the Hamilton-Jacobi equation can be arranged in the power series for x and λ₀ as follows:

Balancing Eq. (22) for like kinds of variables results in the ordinary differential equation for the coefficients of Taylor expansion. It turns out that the initial condition F₂(x, λ₀ t = t₀) = x(t₀)^Tλ₀(t₀) satisfies Eq. (18). The F₂ can now be developed by propagating the initial value problem of the ordinary differential equations for the coefficients of Taylor expansion of generating functions until the desired final time. Then, the Legendre transformation converts the F₂ into the F₁ algebraically:

After introducing the boundary conditions for the reconfiguration problem, the initial costate vector and the performance index are expressed as follows (Park et al. 2006):

The steps up to Eq. (24) show that the optimal control problem can be converted into the IVP, not the TPBVP, without any iterative procedure for determining the initial costate. Eqs. (24) and (25) state that it is necessary to obtain the associated generating function only once. That is, the initial costate vector and performance index can be obtained by simply introducing the given boundary conditions into Eqs. (24) and (25). These characteristics can be advantageous in solving for a number of boundary conditions and time spans for multiple satellites in formation.

In order to demonstrate the convergence of trajectories and performance index based on generating functions to a nonlinear reference solution, the linear, second and third order solutions are developed by using our approach. The expanded generating function and their coefficients are obtained by the Mathematica-based HJ package developed by Guibout, which implemented all the steps from Eq. (14) to Eq. (23) (Guibout & Scheeres 2004). The nominal solution for obtaining the generating function is defined as 0 which is a trivial equilibrium solution of the RSW coordinate system. The initial costate vector satisfying the boundary conditions is determined from the F₁ generating function by Eq. (24), which allows one to integrate the Hamiltonian system with the given state vector to develop an optimal trajectory. The performance index is obtained by substituting the boundary conditions into Eq. (25).

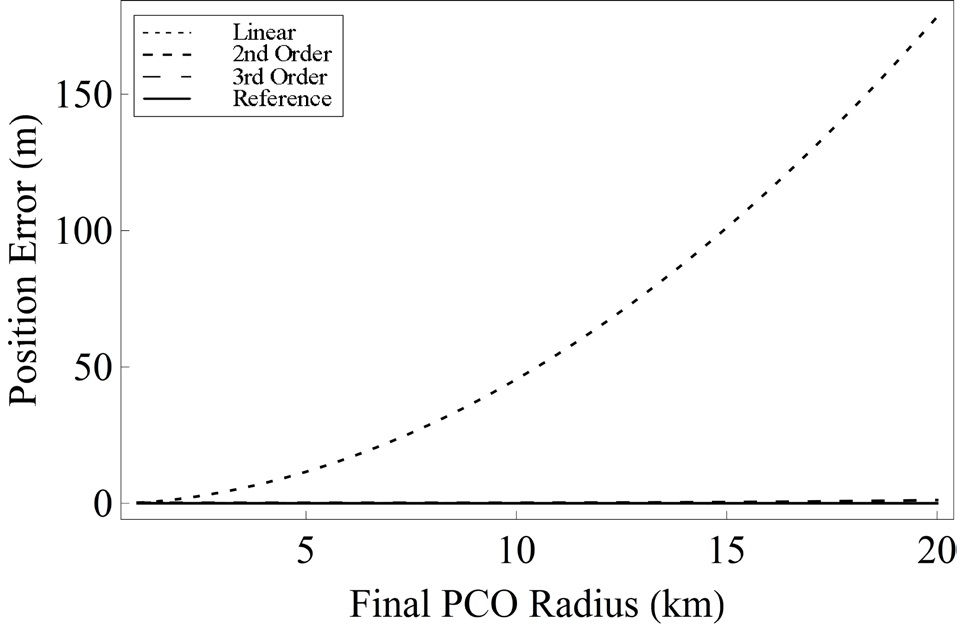
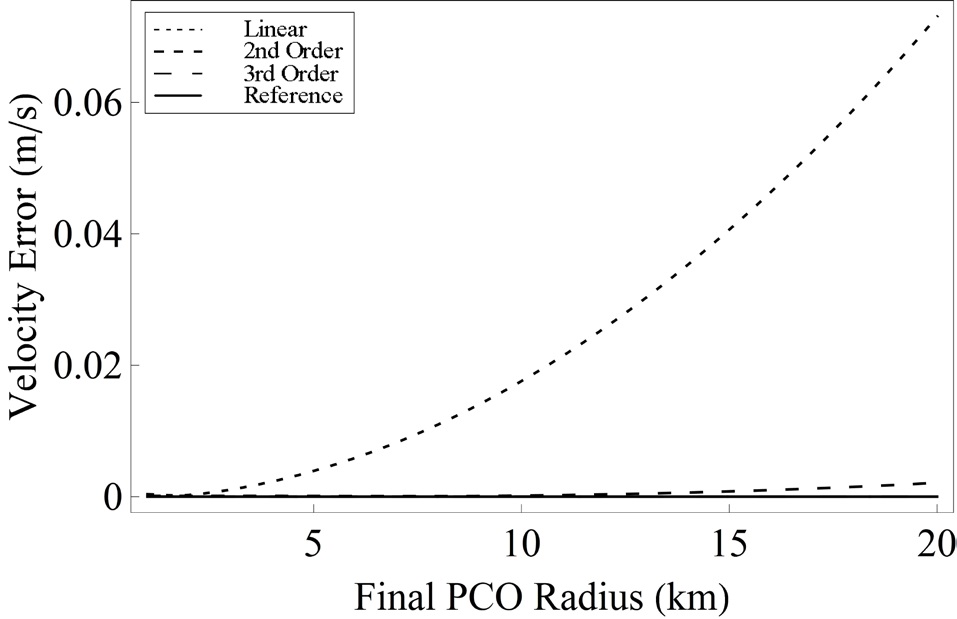
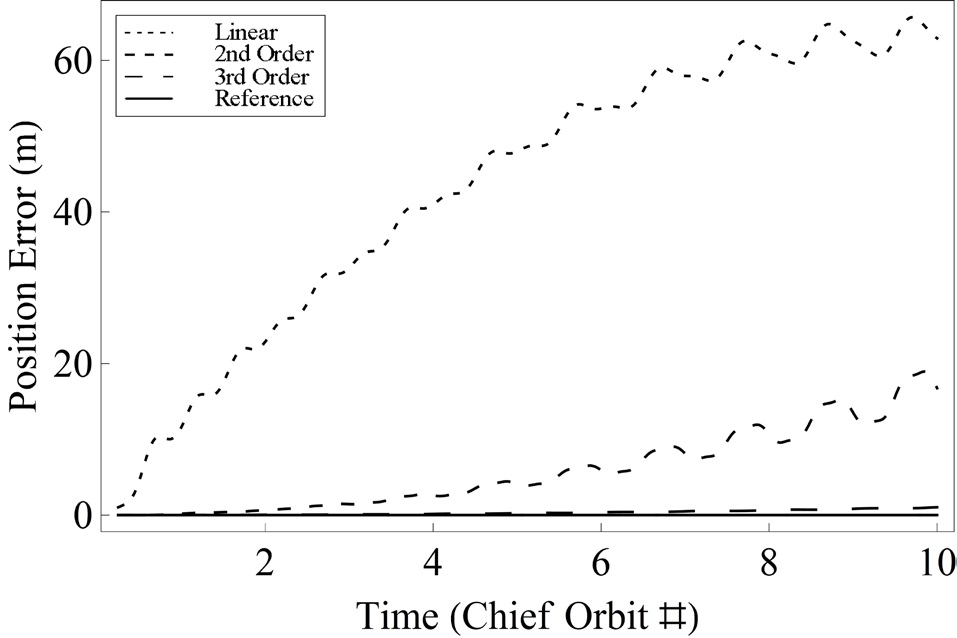
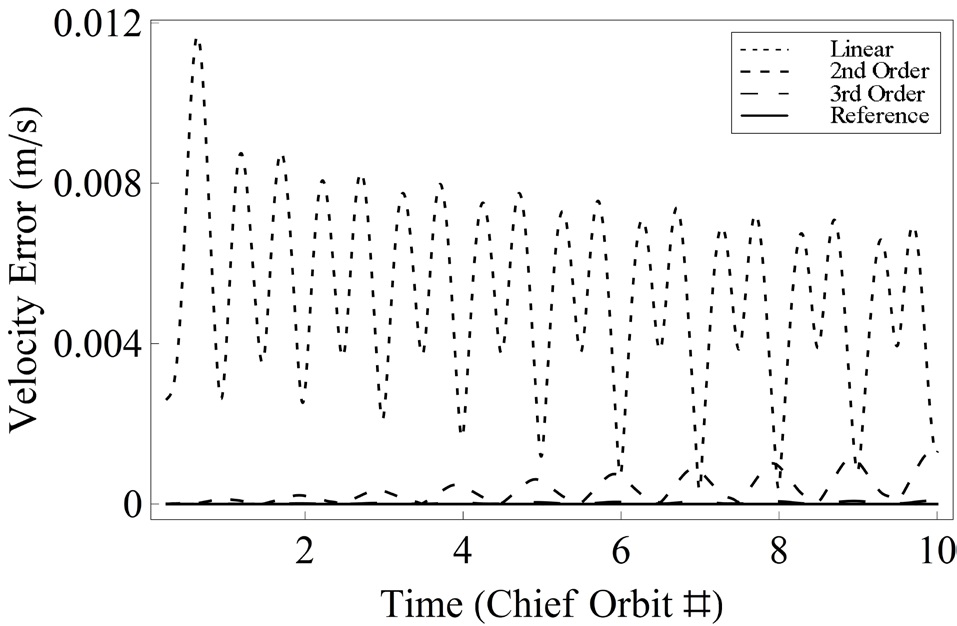
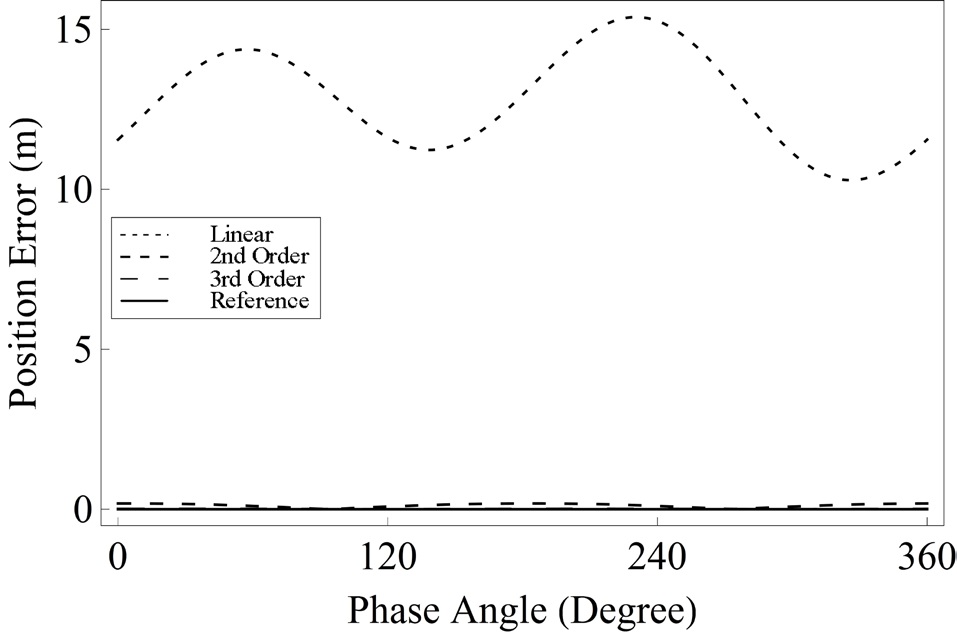
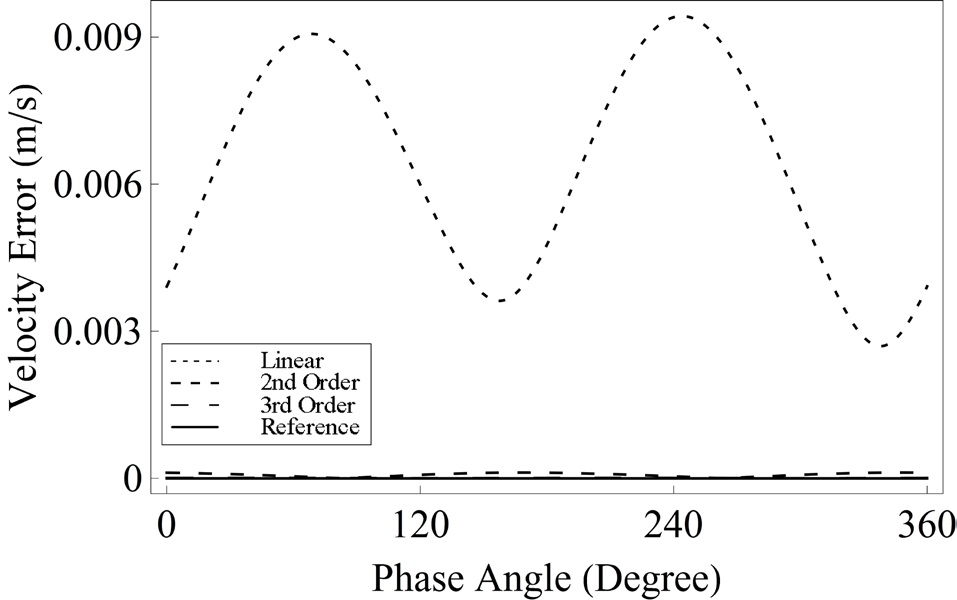
As a verification of the convergence of solution based on generating functions to a nonlinear reference solution, the satisfaction of the prescribed boundary conditions is tested through the error analysis. The linear, second and third order solutions based on generating functions are compared with the reference solution obtained from a numerical shooting method. For error analyses, the position and velocity vectors are considered separately, and are compared with prescribed terminal boundary conditions. In order to describe various formation reconfiguration examples, three cases are addressed as follows:

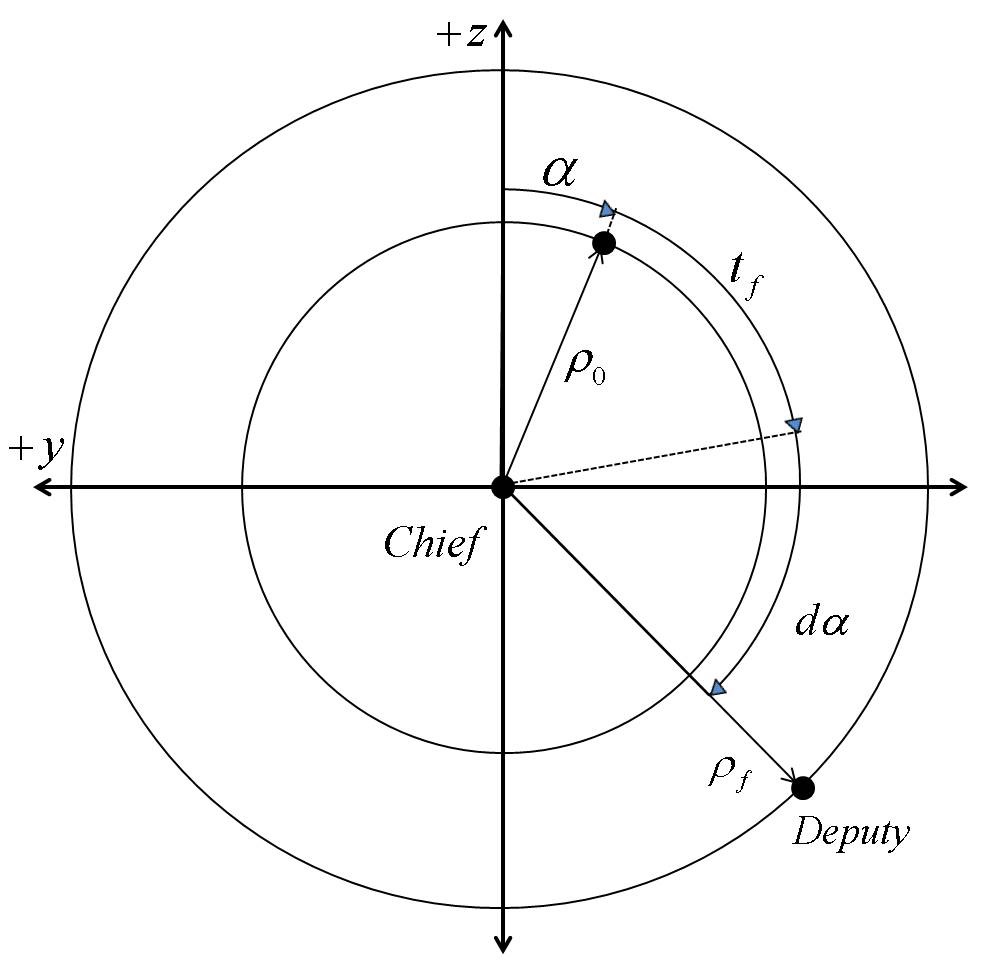
Case 1. Errors according to the change of ρf

Case 2. Errors according to the change of tf

Case 3. Errors according to the change of α

Fig. 2 represents the configuration parameters defining the boundary conditions on the PCO. ρ₀ and ρ_f are the radius

of the PCOs before and after reconfiguration, respectively. α is the phase angle of the initial PCO and △α is the increment in phase, and t_f is the transfer time. Note that both △α and (normalized) t_f are combined to represent total increment in phase. In all examples, the orbital period P and the radius of circular reference orbit R_ref are given as

where μ is the gravitational constant of the earth.

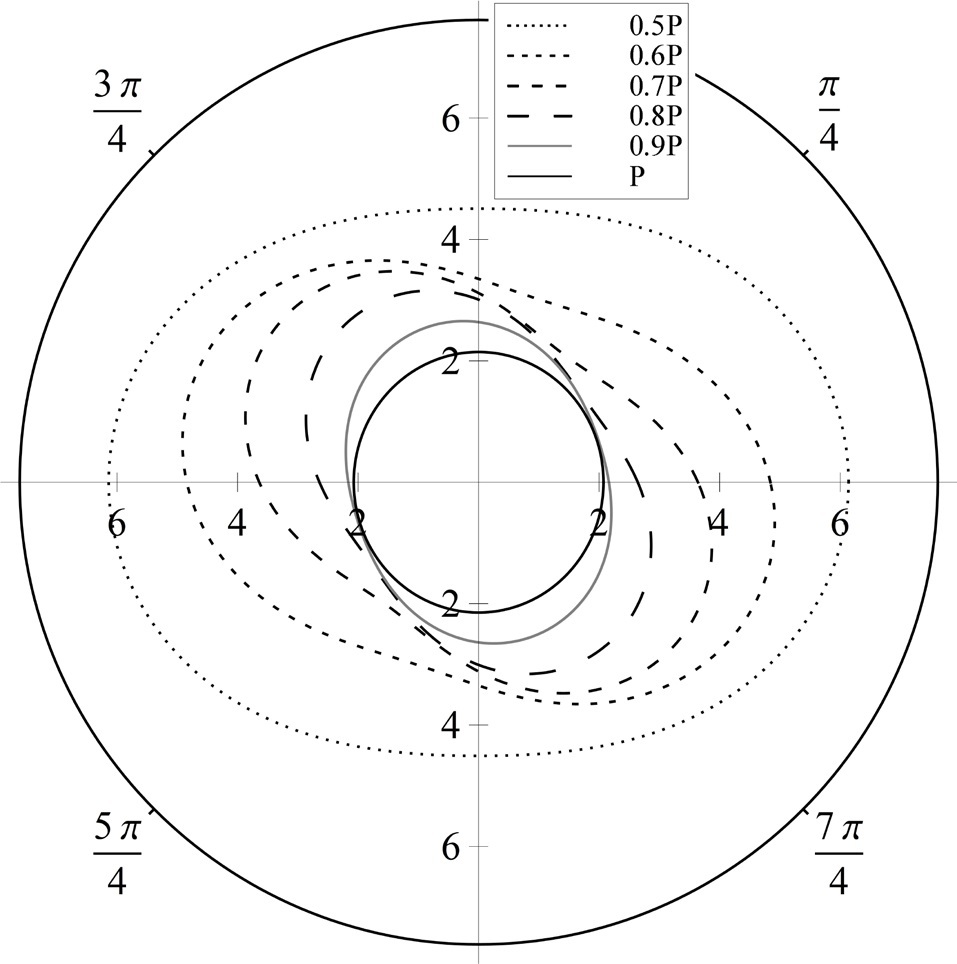
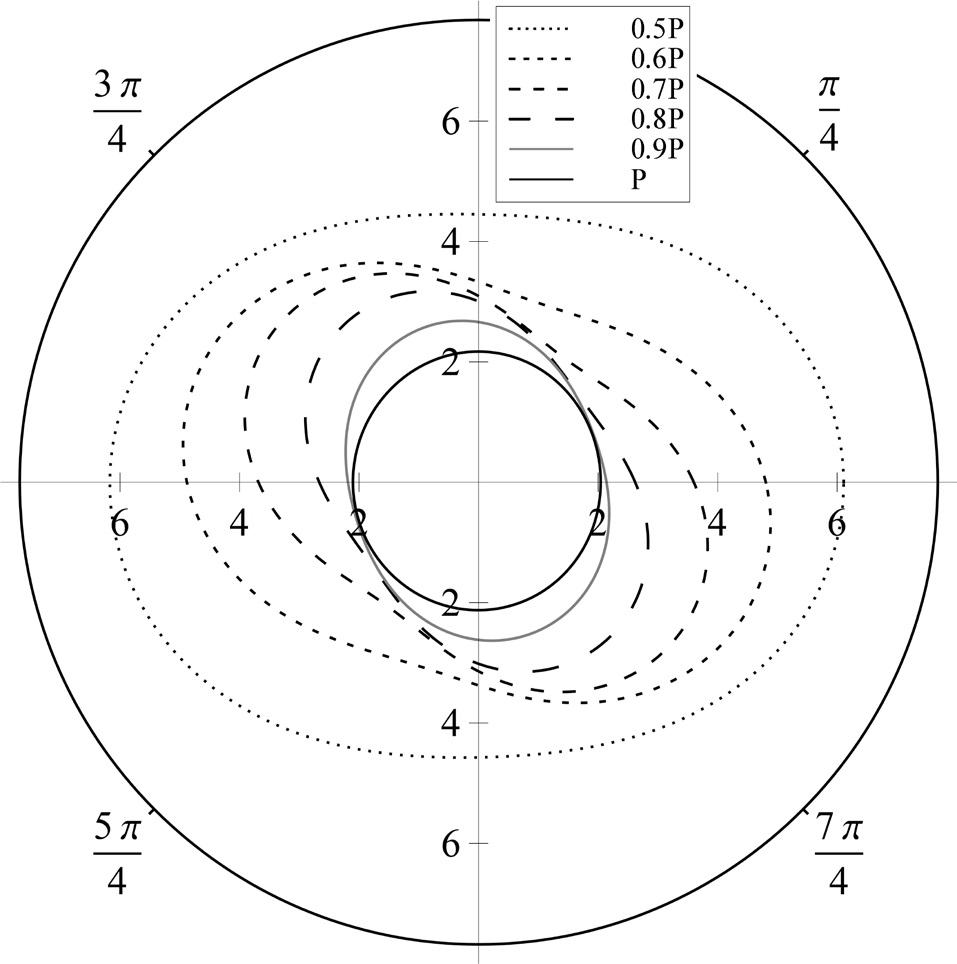
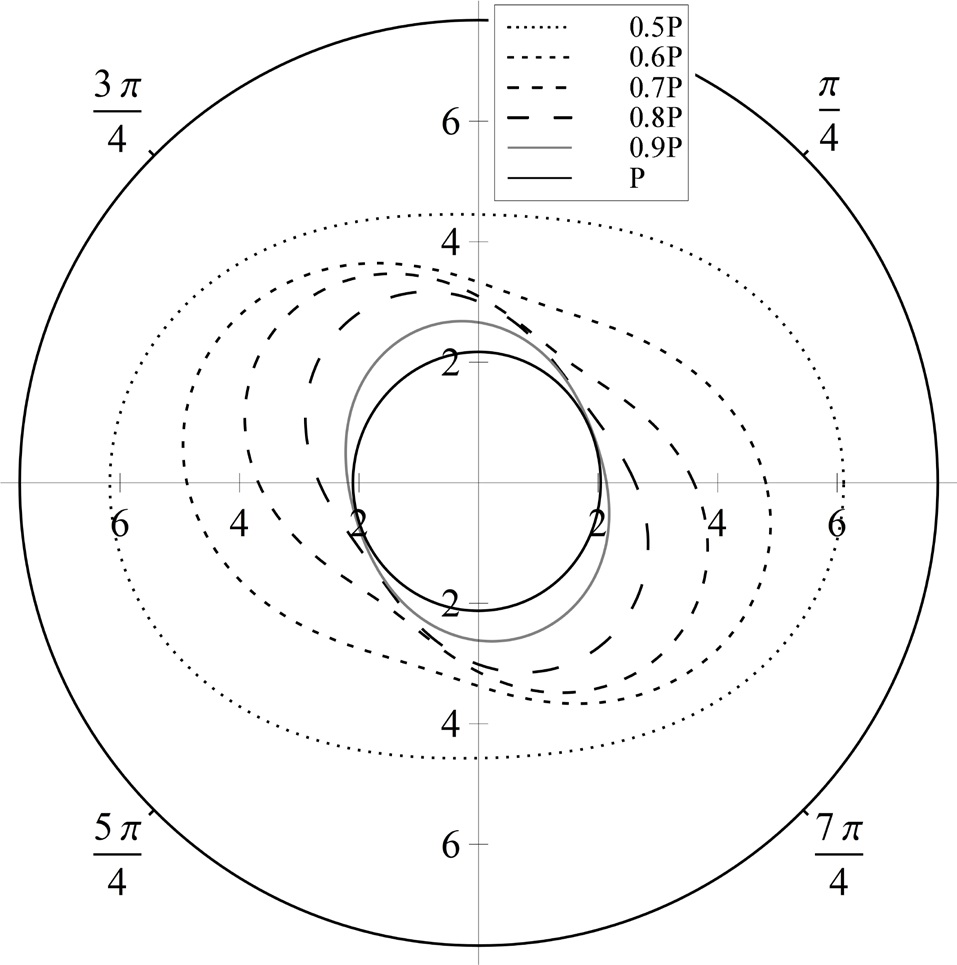
The position and velocity errors for Cases 1, 2 and 3 are presented in Figs. 3-8, respectively. The fixed configuration parameters for each case are given as follows:

In Figs. 3 and 4, while the position and velocity errors of the linear solution steadily increase as ρ_f increases, those of the second and third order solution are kept consistently low. The results of Case 2 and Case 3 show similar tendencies. Unlike the errors of the linear solution, those of the second and third order solution closely track the error of the nonlinear reference solution. Especially, the errors of the third order solution are quite close to those of the reference solution. As the errors of Cases 1-3 are displayed by changing different PCO configuration parameters, it is confirmed that the higher-order solution based on the generating function provides more accurate solutions than the linear solution for varying boundary conditions considered in the nonlinear optimal reconfiguration problem.

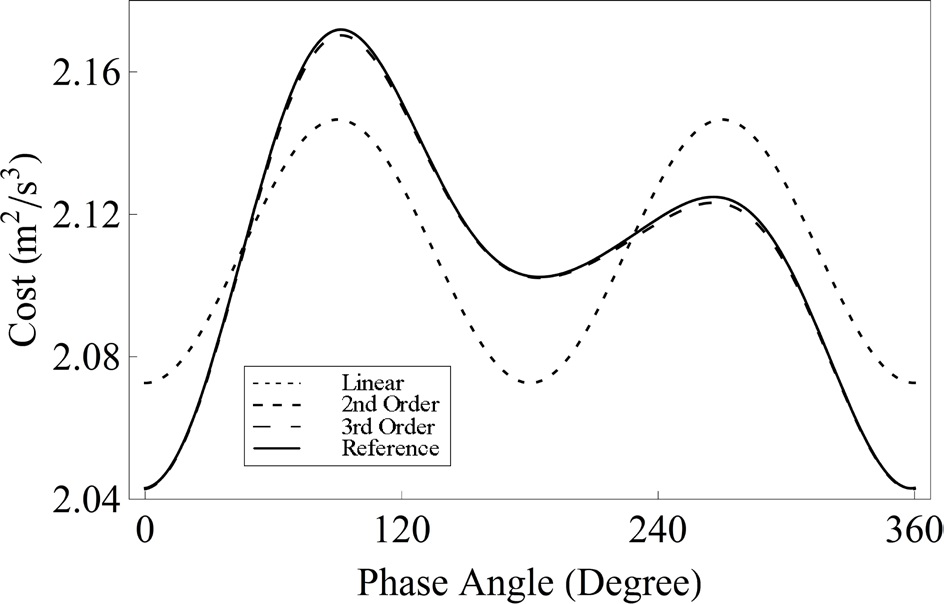
In this section, the performance index based on generating functions is compared with that from a numerical shooting method. The performance index is displayed by varying the initial phase α and the operation time span t_f , with other parameters fixed. While the performance indices of the linear to third order solutions are obtained from Eq. (25), that of the nonlinear reference solution is obtained from numerical integration. In addition, the performance index for the nonlinear dynamics shows some distinct characteristics from that for the linear Hill dynamic system. In the PCO reconfiguration problem based on the normalized linear Hill dynamic system, the phase angle α^* which gives the minimum performance index can be obtained as follows (Yoo et al. 2007).

The period and radius of the reference orbit for all examples are defined in Eq. (26).

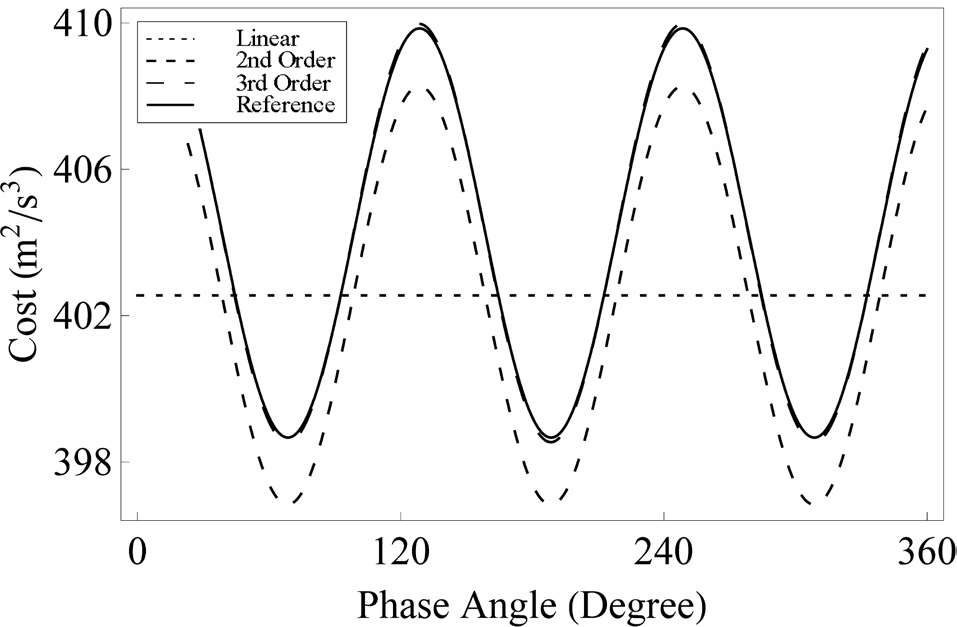
Fig. 9 shows the performance index variation according to the initial phase α with t_f = P. Other fixed parameters are given as follows:

As shown in Fig. 9, the performance index variation by the initial phase α from the second and third order solutions are close to that from the numerical shooting method. Especially,rmance index of the third order solution approximates the numerical performance index quite closely. Fig. 9 allows us to analyze α^* in the nonlinear dynamic system. Whereas two α^*’s exist symmetrically in case of the linear solution, which can be confirmed by Eq. (30), only one α^* has the minimum performance index in case of the second and third order solutions as well as the nonlinear reference solution.

Figs. 10-12 show the performance index variation by varying the initial phase α for a different transfer time t_f, where the phase angle α is expressed in radians and the distance from the origin is the magnitude of the performance index of the associated phase. Fixed parameters in Figs. 10-12 are as shown in Eq. (31). The polar graph of the performance index shows that the optimal initial phase α^* changes gradually as the transfer time t_f changes. This change appears similarly in both the linear and nonlinear solutions. However, whereas two α^*’s exist for the linear solution in the symmetric form, only one α^* appears in the third order solution as well as the nonlinear reference solution. This result confirms the analysis in Fig. 9 that only one α^* exists if nonlinearity prevails.

When a number of satellites maneuver on the PCO, it is often considered that satellites should be distributed uniformly

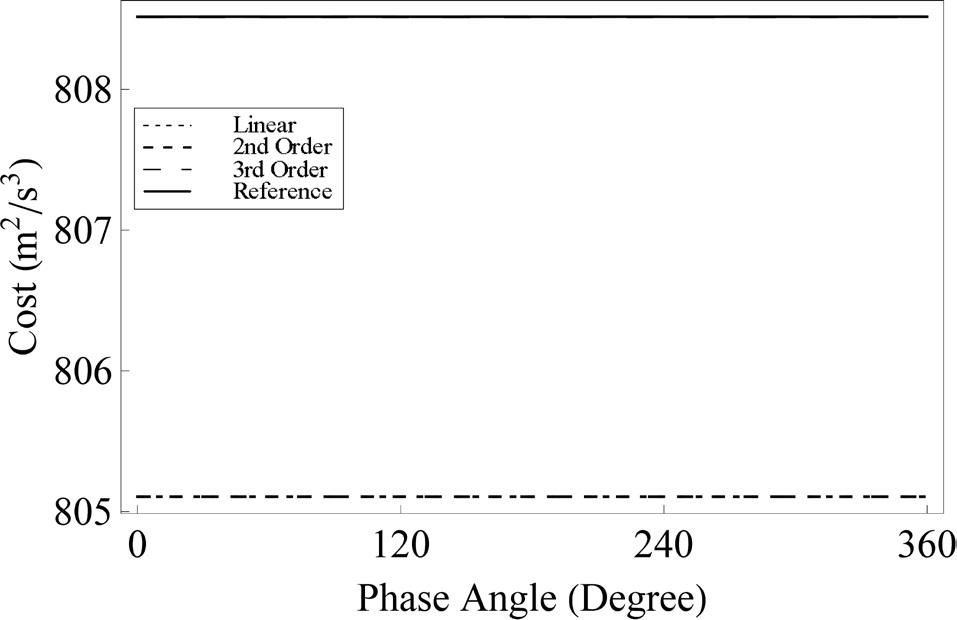
before and after reconfiguration for space interferometry. Figs. 13 and 14 show the sum of performance indices for three and six satellites that perform reconfigurations in equidistant intervals in terms of the initial phase α of the reference deputy satellite.

Other constant parameters are set as follows.

Figs. 13 and 14 show that the sum of performance indices of the third order solution properly approximates that of the nonlinear reference solution obtained from the numerical shooting method. Fig. 13 shows the case of three satellites performing the reconfiguration, in which only the sum of performance indices of the linear solution has a fixed value regardless of α of the reference deputy satellite; those of the nonlinear solution show periodic variations. Even though the boundary conditions in Eq. (32) represent big differences in the initial and terminal PCO radius, and thus possibly incur high nonlinearities of the central gravity field of the earth, Fig. 14 shows that for six satellites, the sum of performance indices in both the linear and nonlinear solutions always shows a fixed value regardless of α of the reference satellite. This phenomena turns out to be consistent, as long as the number of satellite is more than 6.

The optimal control problem for the formation reconfiguration on the PCO has been solved using the generating function. The higher-order solution obtained by using the generating

function converges to the nonlinear reference solution without any iterative procedure of obtaining the initial costate for the various boundary conditions in the nonlinear dynamic system. The semi-analytical performance index derived from the generating function closely approximates the performance index obtained from the direct numerical integration. It allows us to analyze performance index characteristics of the nonlinear formation reconfiguration, which shows distinct patterns from the linear reconfiguration. The analysis for the errors and performance indices demonstrate that the generating function approach is an appropriate method for nonlinear optimal reconfiguration of formation flying satellites. In the future, the generating function approach will be applied to more general case of perturbed elliptical reference orbit.