Composite materials have various applications in many engineering structural fields. Especially, aerospace structures require high stiffness and strength to weight ratio. These applications have required accurate prediction of the thermo-mechanical behavior of composite laminates for the design and analysis of structural composite. Therefore, advanced composites have been used continuously and have been expanded in their application for the last three decades. Numerous theories (Pagano, 1969; Pagano, 1970; Reddy, 2004) have been developed for the accurate analysis of laminated composite structures. Several equivalent single layer (ESL) plate theories (Reddy, 2004) are developed by assuming the form of the in-plane displacement field as a linear combination of unknown functions and the thickness coordinate. The first ESL theory is a classical laminated plate theory (CLPT), based on the Kirchoff-Love plate assumption that the in-plane displacement remains normal to the centerline of the plate after deformation. Improved theory over CLPT is a first-order shear deformation theory, which considers the transverse shear deformation of the plate which requires the shear correction factor. Even though the FSDT is more reliable than the CLPT, it still cannot accurately predict the mechanical behaviors for the laminated composite plates. Thus, more advanced theories have been required, and a series of the smeared higher order theories (Lo et al, 1977; Reddy, 1984) have been developed for the laminated composite plates. For instance, the third-order shear deformation theory uses a cubic polynomial for the in-plane displacement field. In TSDT, there is no need to use the shear correction factor. Among the advanced theories, efficient higher order plate theory (EHOPT), developed by Cho and Parmerter (1993), demonstrates the best performance among displacement-based zig-zag theories. It has been recognized that the zig-zag pattern of in-plane displacement provides the accuracy analysis of deformation and stress.

Meanwhile, in all of the above ESL theories, the material properties of composite laminates have been considered as linear elastic materials. In reality, composite laminates are inhomogeneous materials which are composed of a viscoelastic matrix and elastic fibers as reinforcement (Yi, Pollock, Ahmad and Hilton, 1994). Hence, like other viscoelastic materials, the mechanical behavior of fiber reinforced composites leads to creep strain, stress relaxation and time-dependent failure. These viscoelastic behaviors are critical when the composite laminates are in high temperature or vibrating conditions. Several researches (Hilton and Yi, 1993; Aboudi and Cederbaum, 1989) have analyzed the dynamic response of composite laminates considering the viscoelastic effects. For example, Srinatha and Lewis (Srinatha and Lewis, 1981) suggested a numerical procedure which solved an integral problem using the trapezoidal integration method for the Boltzmann superposition integral. As a result, the accuracy of the results depends on a time step Δt. However, it requires extensive computational time to obtain the reliable results by reducing the size of each time step, especially for long-term problems. Other researchers (Chen, 1995; Hilton and Yi, 1993) solved the problem of computational cost by using the Laplace transformation for a viscoelastic beam. The results in the real time domain were obtained by the inverse Laplace transformations based on numerical calculation.

In the present study, the mechanical behavior of viscoelastic composite laminates is investigated using the Laplace transformation based on the FSDT and TSDT. By applying Laplace transformation instead of the direct time integrations of the Boltzmann superposition integral and directly inversing the equations in the Laplace domain to the real time domain, the accuracy increases significantly as much as that of elastic counterparts. In addition, since the viscoelastic constitutive equation has the form of integration, the top and bottom stress free conditions cannot be directly applied in the TSDT model. Thus, based on the Laplace transformation, top and bottom stress free conditions are successfully applied in the Laplace domain, which makes the theoretical formulation very simple. The present theory considers viscoelasticity in two basic models: Maxwell and Kelvin for viscoelastic phenomena such as creep, cyclic creep and recovery. More complex models with extended Prony series can be developed from these basic models.

The presented and discussed numerical results focus on: (1) the comparison of deflections by using the FSDT and TSDT for elastic composite laminates; (2) the deflection of both elastic and viscoelastic composite laminate; (3) the influence of viscoelastic coefficients to dynamic responses of composite laminates; (4) the in-plane displacement of viscoelastic composite laminates.

Instead of Hook’s law, the stress-strain relation for linear viscoelastic materials can be expressed by Boltzmann superposition integral equations:

where t is time, τ is time variable of integration, and σ_ij(t) and ε_kl(t) are the time-dependent stress and strain, respectively. J_ijkl(t) is the compliance and Q_ijkl(t) is the relaxation modulus which can be approximately determined by Prony series:

where the relaxation modulus E_ijkl,0, E_ijkl,p and the coefficient a_p can be determined from experimental relaxation curves.

In the present study, the viscoelastic material is modeled by following both Maxwell and Kelvin models. The relaxation modulus for the Maxwell model (Eq. 3) and the compliance modulus for the Kelvin model (Eq. 4) are expressed as time-

dependent simpler forms:

By taking the Laplace transform with respect to time, the Boltzmann superposition integral equation in the Laplace domain can be derived as:

where ( )* are the parameters in the Laplace domain.

It is well recognized that the form of the Boltzmann superposition integral equation in the Laplace domain for viscoelastic material is similar to that of Hook’s law in linear elastic constitutive equations. Hence, it is possible to solve the problem of viscoelastic laminate in the Laplace domain with the same elastic counterpart.

In this paper, we consider a linear plate model with the thickness h, and the length L. The geometry and coordinates of the laminated composite plate are shown in Fig. 1. Based on the Reissner-Mindlin plate theory which analyzes for firstorder transverse shear deformation, the time dependent displacement field across the laminate thickness can be expressed in the following form:

where u_α⁰ and w are displacements defined at the mid-plane of the laminated plates.

Due to the linearity of the Laplace transform, the displacement field in the Laplace domain can be written as,

In the present theory, the virtual work principle for quasistatic viscoelastic problems is described as:

where v is viscoelastic solid volume, and a is the surface on which the distributed loads p is applied.

Substituting the displacement fields into the virtual work principle and applying Laplace transform, the equilibrium equations can be obtained:

where stress resultants are defined as follows:

The resultants in the Laplace domain can be expressed as follows:

where stress resultants A^r_αβγδ are defined as follows:

For both static and harmonic loadings, the cylindrical bending behavior of the composite plate is analyzed. Thus, all of the equilibrium equations are reduced to the one dimensional form. The displacement variables are assumed as a trigonometric form by considering the simply supported boundary. In the time domain, the displacement and transverse load can be chosen to be of the forms:

where α=n/L;p_n(t) is the external load; p_n(t)= P_nsin(ωt) for harmonic loading, and p_n(t)= P_n for a static loading case. By substituting Eq. (17) into equilibrium equations, the algebraic relations in the Laplace domain can be obtained as follows:

where [K]_5×5 is the numerical global stiffness matrix with the detail expression which will be shown in the Appendix.

By applying the inverse Laplace transform to Eq. (18), the algebraic relations in the real time domain can be obtained as follows:

where f₅(t) is the time dependent function of force which can be determined for two basic viscoelastic models and both static and harmonic loads.

From Eq. (19), the solutions of (U_n,1⁰, U_n,2⁰, ？_n,1, ？_n,2, W_n) are determined, then the displacements are calculated by substituting the obtained solution into the displacement fields. Therefore, all of the displacement, stress and strain of laminated composite plates can be determined.

Following the third-order transverse deformation, the time dependent displacement can be expressed in the following forms:

where u_α⁰ and w are displacement variables defined at the mid-plane of the laminated plates.

Being identical to Eq. (6)-(7), the displacement fields in the Laplace domain can be written as:

The number of the unknown variables is reduced by applying top and bottom surface traction free boundary conditions as follows:

Similar to FSDT analysis, substituting the displacement fields into the virtual work principle and applying Laplace transformation, the equilibrium equations can be obtained as follows:

where the added stress resultants are defined as:

The resultants in the Laplace domain can be expressed as follows:

where stress resultants A^r_αβγδ are defined similarly in the FSDT and G^r_αβγδ are defined as follows:

Executing the same procedure as the FSDT case, the algebraic relations can be obtained as follows:

where [K]_5×5 is the numerical global stiffness matrix with the detail expression which will be shown in the Appendix.

By applying the inverse Laplace transform to Eq. (32), the algebraic relations can be obtained as follows:

From Eq. (33), the solutions of (U_n,1⁰, U_n,2⁰, ？_n,1, ？_n,2, W_n) are determined, then the displacements are calculated by substituting the variables into the displacement fields. Therefore, all of the displacement, strain and stress of laminated composite plates can be determined.

To compare the present analysis with the results of the previous study and other theories, the [0/90/0] laminated composite plate is chosen as an illustrative numerical example. The material properties of the ply are:

where L denotes the direction of the fiber and T denotes the direction perpendicular to the fiber. The shear correction factor for FSDT is chosen as k=5/6. The viscoelastic coefficient a_M for the Maxwell model and a_K for the Kelvin model are assumed as:

To show the influence of the viscoelastic coefficient to mechanical behavior especially transient time, the coefficients a_M and a_K are assumed in the following range:

for both static and harmonic loadings.

The displacements are normalized by the following nondimensional values:

where S represents the length to thickness ratio, which is defined by S=L/h.

The numerical examples consider both static and harmonic loads which are shown in Fig. 2. The static loading, which is constant with respect to time, is presented as follows:

where u(t) is the Heaviside unit step function which presents the recovery process of viscoelastic creep, and the recovery time t₀=12s. The harmonic loading is presented as follows:

where ω is the frequency which is chosen to be small enough for the static problem (ω=1s^-1).

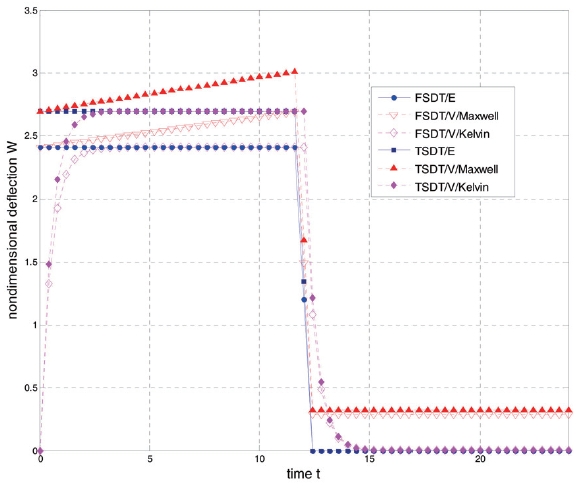
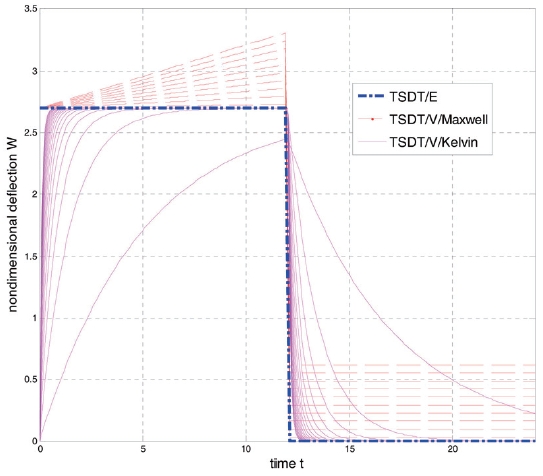
Fig. 3 shows the nondimensional deflection W for the creep and creep-recovery process based on FSDT and TSDT. The letter E means the analysis for the elastic solution; V indicates the analysis for the viscoelastic case. The responses of both FSDT and TSDT methods have good agreements for the deflection behavior of the Maxwell and Kelvin models. For the Maxwell model, the value of nondimensional deflection increases linearly with respect to time from We (W_e=2.409 with FSDT and W_e=2.699 with TSDT), which is the nondimensional deflection in the elastic case. For the

Kelvin model, at transient time, the value of deflection W of the mid-plane increases from 0 to W_e exponentially. For the creep-recovery process, the deflection W of the Maxwell model drops suddenly at t₀ = 12s, and maintains that value constantly; the one for the Kelvin model decreases from W_e to 0. The difference between the FSDT and TSDT is the value of W_e derived from the linear elastic response. All of the above mechanical behaviors have good agreements with the linear viscoelastic creep and recovery responses which were presented by Flugge (1975).

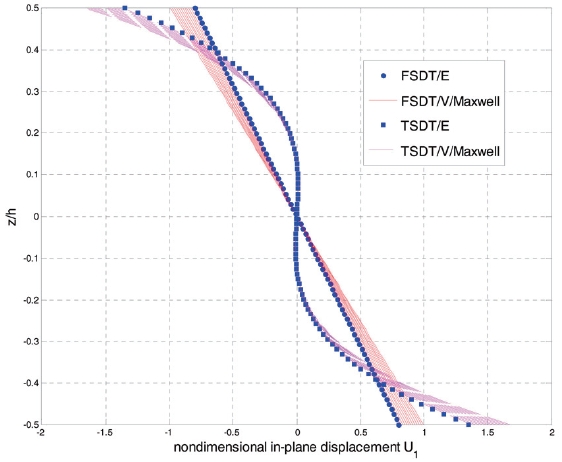
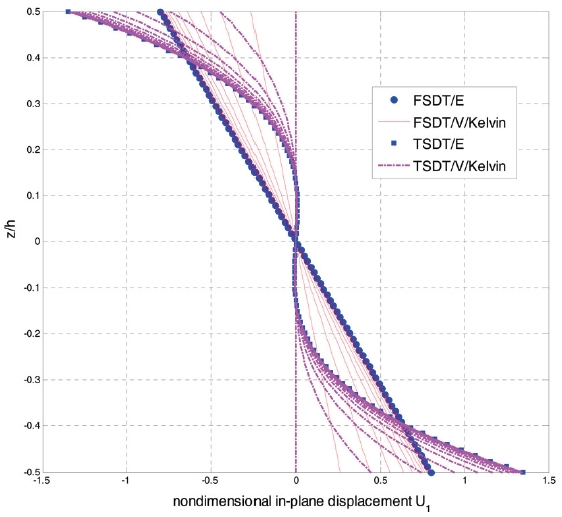
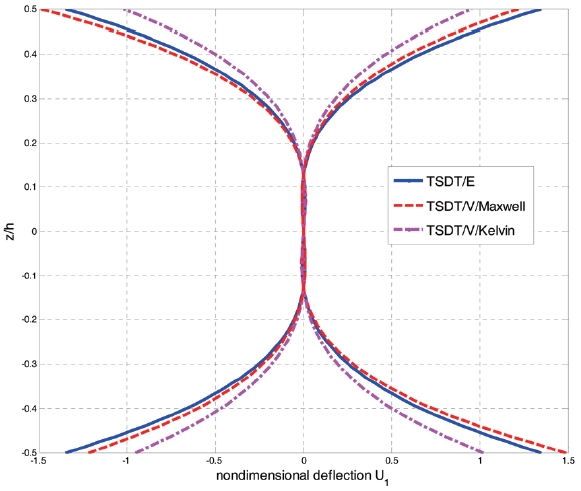
Fig. 4 shows the time-dependent nondimensional inplane displacement U₁ for the Maxwell model based on the FSDT and TSDT. The elastic solution of FSDT is the straight line, but that of TSDT is the cubic line. The in-plane

displacement U₁ for the Maxwell model is greater than that of the elastic solution in time. Fig. 5 presents the timedependent nondimensional in-plane displacement U₁ for the Kelvin model based on the FSDT and TSDT, with the time from 0 to 12s and the time step Δt=0.1s. The displacement for the viscoelastic solution of the Kelvin model increases from 0 to the bound of the linear elastic solution at transient time. After that, the elastic and viscoelastic cases have nearly the same responses.

Fig. 6 shows the influence of viscoelastic coefficients for the Maxwell and Kelvin model to the deflection of the midplane for the TSDT. For the Maxwell model, the angle ？_M between the viscoelastic line and horizontal elastic line can be determined as follows:

where K is the stiffness matrix. When the value a_M decreases, the angle ？ also decreases. Thus, the solution is close to the elastic one. In contrast, for the Kelvin model, when a_K increases, the deflection of the viscoelastic solution is closer to the elastic one for both creep and creep-recovery. In some cases, with a small value of a_K, the deflection W does not have enough time to obtain W_e. Thereby, there is an amount of difference ΔW known as viscoelastic damping.

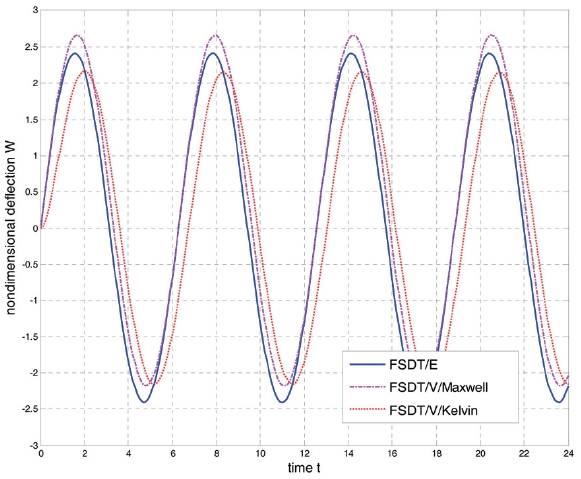
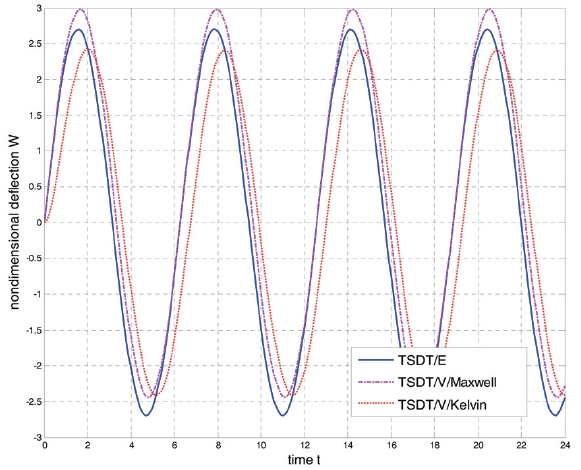
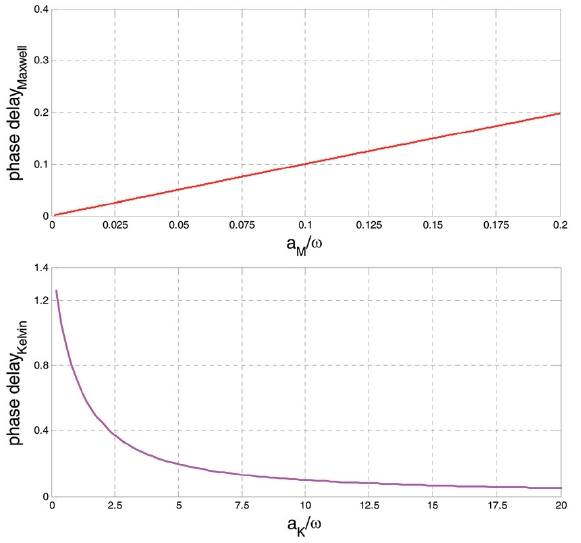
Fig. 7 and 8 show the time-dependent nondimensional deflection W based on the FSDT and TSDT, respectively. Both methods present similar viscoelastic behavior for Maxwell and Kelvin models. For the elastic model, which

is represented as a continuous line, the displacement has the same phase with the harmonic loading Δφ=0. For both viscoelastic models, there are phase delay Δφ_M and Δφ_K. For the Maxwell model, the center of deflection changes from 0 to W_M depending on the Maxwell viscoelastic coefficient a_M and the frequency ω of harmonic loading. The amplitude of deflection fluctuation of the viscoelastic solution is greater than the elastic one. The difference depends on the a_M/ω ratio. For the Kelvin model, the amplitude of fluctuation is smaller than that of the elastic model.

Fig. 9 presents the time-dependent nondimensional in-plane displacement U₁ for the Maxwell and Kelvin models based on the TSDT at the time when the inplane displacements have the maximum or minimum values. From these lines, the region of fluctuation of the

viscoelastic response for both Maxwell and Kelvin models are distinguished clearly. The fluctuation region of the elastic case is limited by two continuous lines; the one of viscoelastic case with the Maxwell model is limited by the discontinuous line, and the one with the Kelvin model is limited by the two dot-dashed lines. The amplitude of U₁ for the Kelvin model is smaller than the one of the elastic model. For the Maxwell model, there is a center difference which depends on both the viscoelastic coefficient and frequency of external loading.

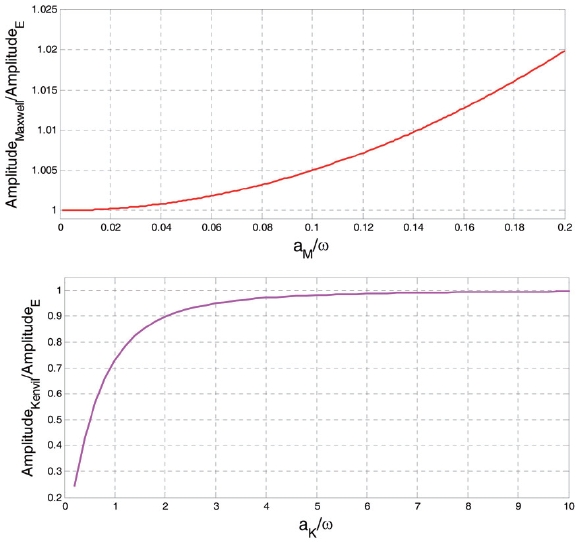
Fig. 10 shows the effect of the viscoelastic coefficient to the amplitude of deflection in the case of harmonic loading. The upper figure is for the Maxwell model and the lower one is for the Kelvin model. With the small value of a_M/ω, the influence of the viscoelastic coefficient is insignificant, and the amplitude ratio of the Maxwell and elastic model is approximately 1. This ratio of amplitude increases when a_M/ω increases. Fig. 11 presents the influence of the viscoelastic coefficient to the phase delay of the deflection in the case of harmonic loading. The upper figure of Fig. 11 for the Maxwell model shows that when increasing the value of ratio a_M/ω, the phase delay increases linearly. In contrast, as presented in the lower figure of Fig. 11 for the Kelvin model, the phase delay decreases when increasing the ratio a_K/ω.

The mechanical behaviors of linear viscoelastic composite laminates have been analyzed by applying the Laplace transform without any integral transformation or any time step scheme. The numerical examples for static and harmonic loading under the quasi-static assumption show the creep responses of viscoelasticity for both the FSDT and TSDT cases. For the harmonic loading, the results of both basic models demonstrate the phase delay and the change of amplitude of deflection compared to the elastic one. For static loading, the Kelvin model has a better analysis for creep responses than that of the Maxwell model, especially in transient time.

For more efficient analysis, a higher-order cubic zig-zag theory such as efficient higher order plate theory (Cho, 1993), needs to be developed in the environment of viscoelastic behavior. In addition, a time-dependent relaxation modulus needs to be expresses through general Prony series which was developed in the present study for basic Maxwell and Kelvin models. These are currently under process.

♣ The first row of stiffness matrix K:

♣ The second row of stiffness matrix K:

♣ The third row of stiffness matrix K:

♣ The fourth row of stiffness matrix K:

♣ The fifth row of stiffness matrix K:

♣ The first row of stiffness matrix K:

♣ The second row of stiffness matrix K:

♣ The third row of stiffness matrix K:

♣ The fourth row of stiffness matrix K:

♣ The fifth row of stiffness matrix K:

♣ For static loading

♣ For harmonic loading