In this paper, we focus on efficient construction of tightest matched subtree (TMSubtree) results, for keyword queries on extensible markup language (XML) data, based on smallest lowest common ancestor (SLCA) semantics. Here, “matched” means that all nodes in a returned subtree satisfy the constraint that the set of distinct keywords of the subtree rooted at each node is not subsumed by that of any of its sibling nodes, while “tightest” means that no two subtrees rooted at two sibling nodes can contain the same set of keywords. Assume that d is the depth of a given TMSubtree, m is the number of keywords of a given query Q. We proved that if d ≤ m, a matched subtree result has at most 2m! nodes; otherwise, the size of a matched subtree result is bounded by (d ? m + 2)m!. Based on this theoretical result, we propose a pipelined algorithm to construct TMSubtree results without rescanning all node labels. Experiments verify the benefits of our algorithm in aiding keyword search over XML data.
Over the past few years, keyword search on extensible markup language (XML) data has been a hot research issue, along with the steady increase of XML-based applications [1-12]. As with the importance of effectiveness in keyword search, efficiency is also a key factor in the success of keyword search.
Typically, an XML document is modeled as a nodelabeled tree
rooted at a node
that consists of paths from
rooted at
can be got by removing from
all nodes that do not contain any keyword of the given query in their subtrees, and, according to [8],
can be got by removing from
all of the nodes that do not satisfy the constraint of keywords subsumption.
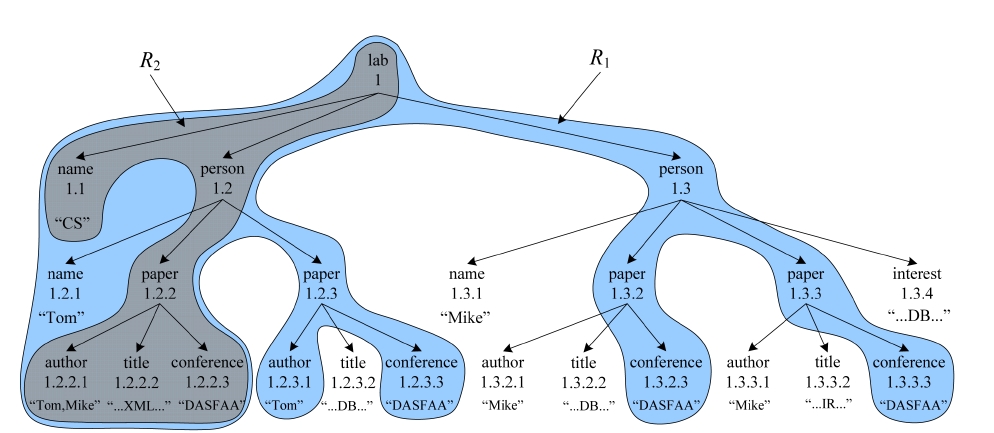
EXAMPLE 1. To find for “CS” laboratory all papers that are written by “Tom” and published in “DASFAA” about “XML” from the XML document
From Example 1 we know that a CSubtree, e.g.,
However, most existing methods [3, 4, 6, 9, 14] that address efficiency focus on computing qualified root nodes, such as SLCA or ELCA nodes, as efficient as possible. In fact, constructing subtree results is not a trivial task. Existing methods [7, 8] need to firstly
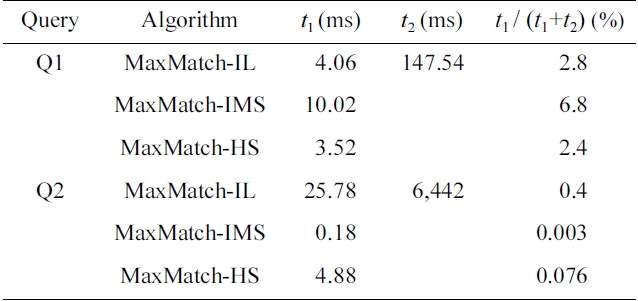
Comparison of the running time for smallest lowest common ancestor (SLCA) computation and subtree construction
labels to compute qualified SLCA/ELCA results, and then
EXAMPLE 2. Take the MaxMatch algorithm [8] for example. It firstly gets the set of SLCA nodes based on either indexed lookup (IL) [4], incremental multiway SLCA (IMS) [6] or hash search (HS) [12] algorithm, then computes all matched subtree results. We ran the Max- Match algorithm for query
From Example 2 we know that, given a set of SLCA nodes, the operation of computing matched subtree results will dominate the overall performance of the MaxMatch algorithm, thus should deserve being paid more attention. As illustrated by [7], an MSubtree could still contain redundant information; e.g., the four conference nodes, i.e., 1.2.2.3, 1.2.3.3, 1.3.2.3, and 1.3.3.3, of
In this paper, we focus on constructing tightest matched subtree (TMSubtree) results according to SLCA semantics. Intuitively, a TMSubtree is an MSubtree after removing redundant information, and it can be generated from the corresponding PSubtree by removing all nodes that do not satisfy the constraint of keywords subsumption, and just keeping one node for a set of sibling nodes that
have the same keyword set. Assume that
to
The rest of the paper is organized as follows. In Section II, we introduce background knowledge, and discuss the related work. In Section III, we give an in-depth analysis of the MaxMatch algorithm [8], then define the tightest matched subtree (TMSubtree) and discuss its properties, and finally, present our algorithm on computing all TMSubtree results. In Section IV, we present the experimental results, and in Section V, we conclude our paper.
† An earlier version of this paper has been published at DASFAA 2012.
II. BACKGROUND AND RELATED WORK
We model an XML document as a node labeled ordered tree, where nodes represent elements or attributes, while edges represent direct nesting relationships between nodes in the tree. Fig. 1 is a sample XML document. We say a node v directly contains a keyword
A Dewey label of node
For a given query
In the past few years, researchers have proposed many LCA-based semantics [1, 2, 4, 5, 11], among which SLCA [4, 6] is one of the most widely adopted semantics. Compared with LCA, SLCA defines a subset of
Based on the set of matched SLCA nodes, there are three kinds of subtree results: 1) CSubtree [2, 4]; 2) PSubtree [13]; and 3) MSubtree, which is a subtree rooted at
To construct MSubtrees, the existing method [8] needs to firstly
Considering that an MSubtree may still contain redundant information (discussed in Section I), in this paper, we focus on efficiently constructing TMSubtree results based on SLCA semantics. Intuitively, a TMSubtree is an MSubtree, after removing redundant information. Constructing TMSubtree results based on ELCA semantics [7] is similar, and therefore omitted for reasons of limited space.
>
A. Insight into the MaxMatch Algorithm
The MaxMatch algorithm [8] returns MSubtree results that are rooted at SLCA nodes, and satisfy the constraint of “keywords subsumption”. For a given query
Step 1 (line 1): MaxMatch finds from the
Step 2 (line 2): MaxMatch calls function
[Table 6.] Algorithm 1 MaxMatch

Algorithm 1 MaxMatch
then sequentially rescan all labels and insert each one to a certain group (if possible), with cost
in this step, all Dewey labels are processed twice to construct the set of groups.
Step 3 (lines 3-5): For each group
}·2
Therefore, the time complexity of Algorithm 1 is
}·2
>
B. The Tightest Matched Subtree
DEFINITION 1. (TMSubtree)
Intuitively, a TMSubtree is an MSubtree with redundant information being removed. It can be generated from the corresponding PSubtree by removing all nodes that do not satisfy the constraint of keywords subsumption, and just keeping one node for a set of sibling nodes that have the same keyword set.
DEFINITION 2. (Maximum TMSubtree)
1)
2)
3)
LEMMA 1. Given a maximum TMSubtree
1) |
2)
3) |
4) if |
In summary, if
THEOREM 1. Given a keyword query
For the 2
child nodes, of which each one contains |
Thus we have Formula 1 to compute the number of nodes at the
If
If
Therefore if
EXAMPLE 3. Given a keyword query
Compared with the MaxMatch algorithm that produces all subtree results in three steps, the basic idea of our method is directly constructing all subtree results in the procedure of processing all Dewey labels. The benefits of our method lie in two aspects: 1) the buffered data in memory is largely reduced; 2) each Dewey label is visited only once. The first benefit comes from Theorem 1, which guarantees that our method does not need to buffer huge volumes of data in memory as [8] does; the second benefit is based on our algorithm.
In our algorithm, for a given keyword query
As shown in Algorithm 2, our method sequentially scans all Dewey labels in document order. The main procedure is very simple: for all nodes that have not been visited yet, in each iteration, it firstly chooses the currently minimum Dewey label, by calling the selectMin- Label function (line 3), then processes it, by calling the pushStack procedure (line 4), and finally, it moves
During the processing, our algorithm uses a stack
The innovation of our method lies in that our method immediately outputs each TMSubtree result
[Table 7.] Algorithm 2 mergeMatching(Q)

Algorithm 2 mergeMatching(Q)
before
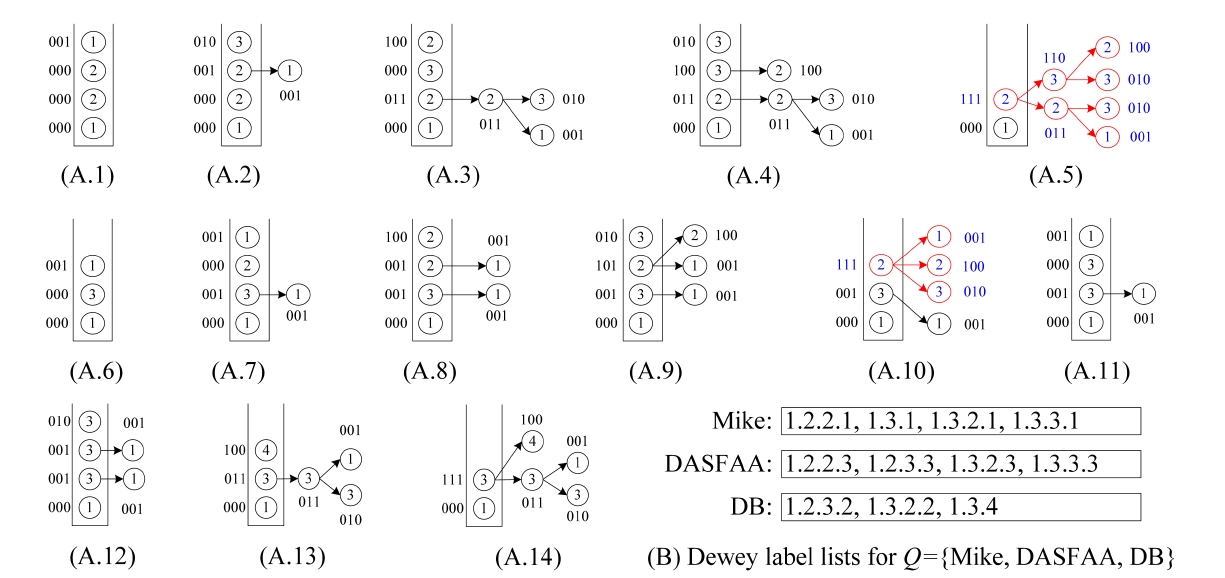
Example 4. Consider the XML document
at 1.3 in line 11 of popStack procedure. Finally, we output the TMSubtree rooted at 1.3.2 in line 10 of Algorithm 2. Therefore for
As shown in Algorithm 2, for a given keyword query
Now we analyze the time complexity of our algorithm. Since our algorithm needs to process all components of each involved Dewey label of the given keyword query
, and the cost of processing these components is
During processing, each one of the
components will be inserted into a subtree and deleted from the same subtree just once, and the cost of both inserting and deleting a component is
Since our method is executed in a pipelined way, at any time it just needs to maintain at most
Note that to output the name of nodes in a TMSubtree result, existing methods may either store all path infor-mation in advance, by suffering from huge storage space [1], or use the extended Dewey labels [17], by affording additional cost on computing the name of each node, according to predefined rules. In contrast, our method
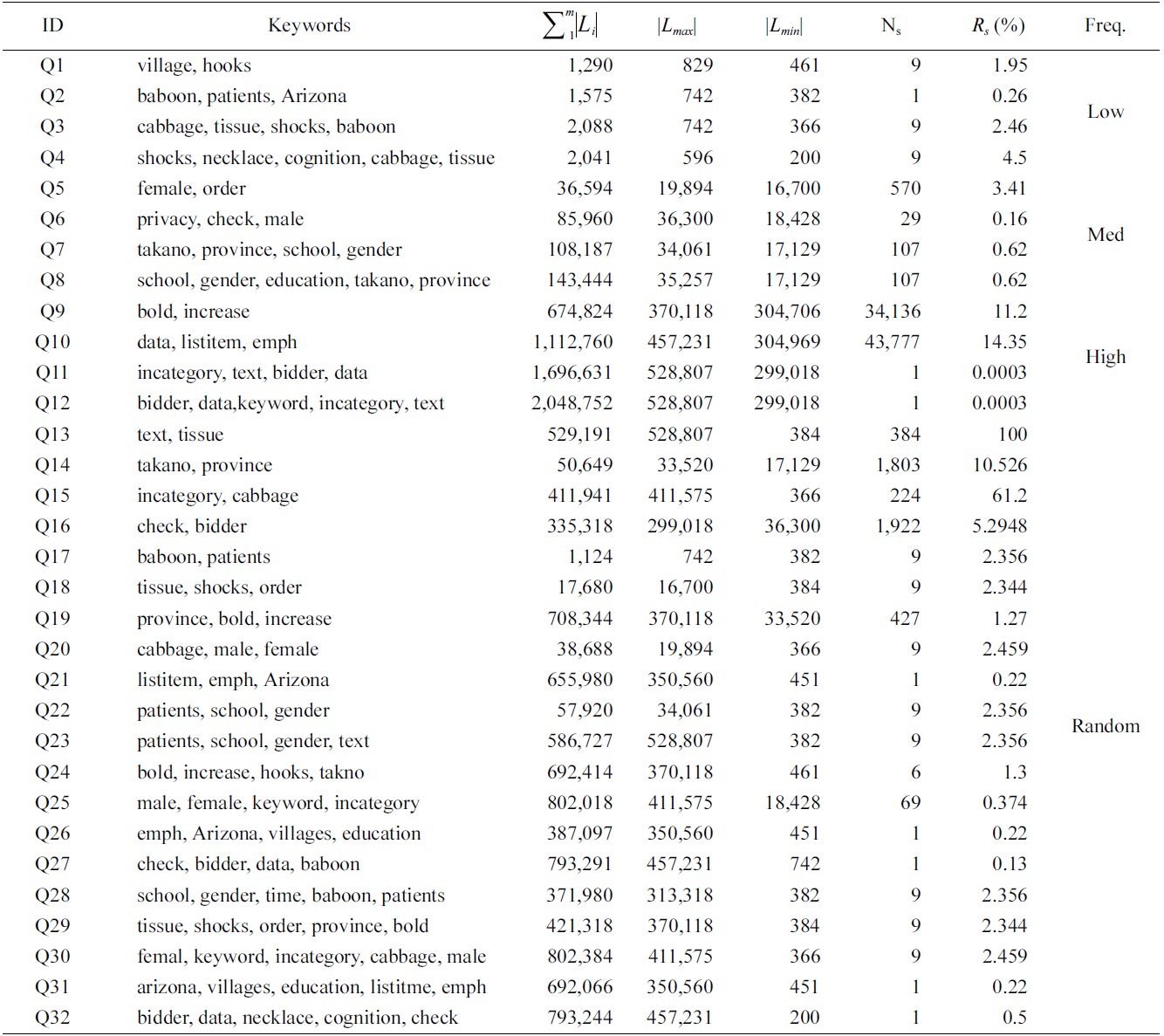
[Table 2.] Statistics of keywords used in our experiment

Statistics of keywords used in our experiment
[Table 3.] Queries on XMark dataset
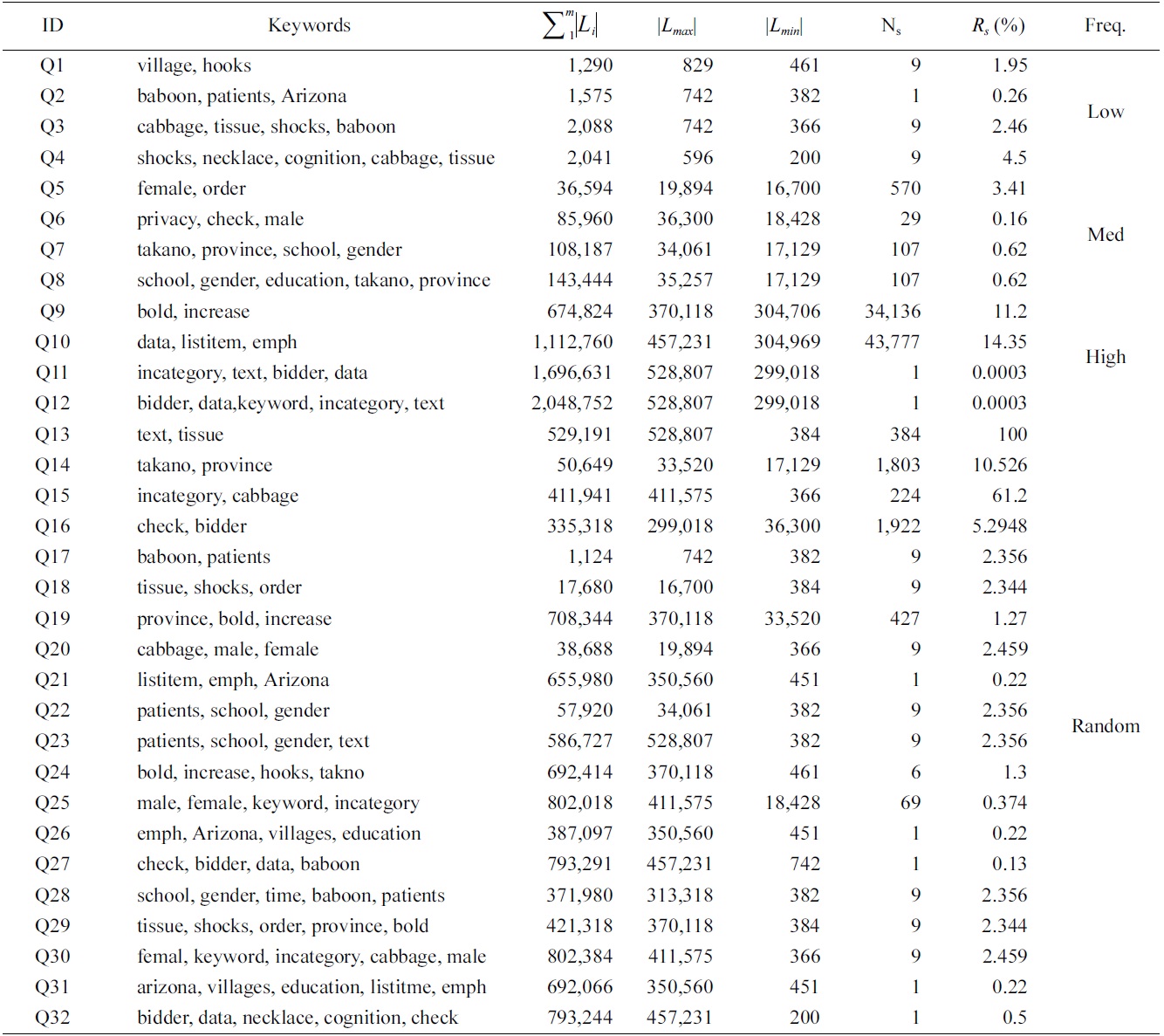
Queries on XMark dataset
maintains another hash mapping between each path ID and the path information; the total number of index entries is the number of nodes in the dataguide index [18] of the XML tree, which is very small in practice. To derive for each node its name on a path, we maintain in each Dewey label a path ID after the last component, thus we can get the name of each node on a path in constant time.
Our experiments were implemented on a PC with Pentium(R) Dual-Core E7500 2.93 GHz CPU, 2 GB memory, 500 GB IDE hard disk, and Windows XP professional as the operating system.
The algorithms used for comparison include the Max- Match algorithm (the MaxMatch algorithm is used to output TMSubtrees in our experiment) [8] and our merge- Matching algorithm. MaxMatch was implemented based on IL [4], IMS [6] and HS [12] to test the impacts of different SLCA computation algorithms on the overall performance, and is denoted as MaxMatch-IL, MaxMatch- IMS and MaxMatch-HS, respectively. All these algorithms and our mergeMatching algorithm were implemented using Microsoft VC+ . All results are the average time, by executing each algorithm 100 times on hot cache.
We use XMark dataset for our experiments, because it possesses a complex schema, which can test the features of different algorithms in a more comprehensive way. The size of the dataset is 582 MB; it contains 8.35 million nodes, and the maximum depth and average depth of the XML tree are 12 and 5.5, respectively.
We have selected 30 keywords, which are classified into three categories, according to the length of their inverted Dewey label lists (the |
Based on these keywords, we generated four groups of queries, as shown in Table 3: 1) four queries (Q1 to Q4) with 2, 3, 4, 5 keywords of low frequency; 2) four queries (Q5 to Q8) of median frequency; 3) four queries (Q9 to Q12) of high frequency; and 4) 20 queries (Q13 to Q32) with keywords of random frequency.
The metrics used for evaluating these algorithms include: 1) the number of buffered nodes, which is used to compare the space cost of these algorithms, 2) running time on SLCA and subtree result computation, and 3) scalability.
For a given query, we define the
>
D. Performance Comparison and Analysis
1) Comparison of the Number of Buffered Nodes
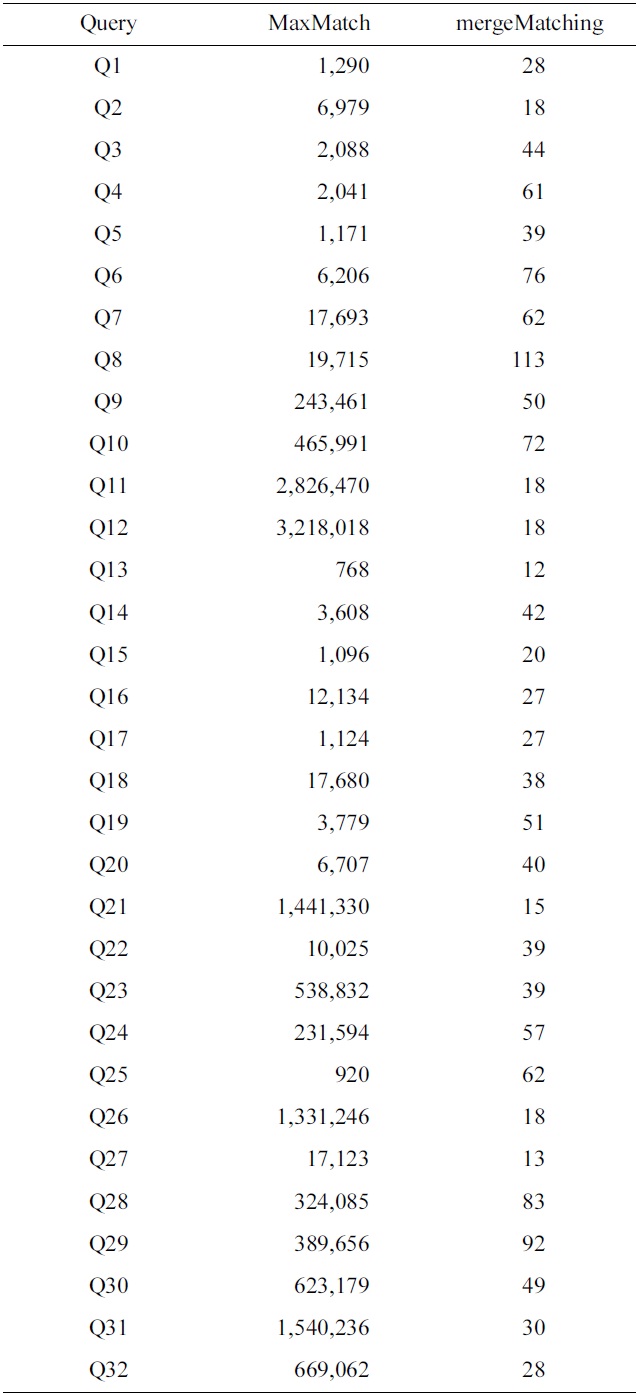
To make comparison of space cost for different algorithms, we have collected the statistics of the number of buffered nodes for the MaxMatch and mergeMatching algorithms. Table 4 shows a comparison of the number of buffered nodes for each query, from which we know that the number of buffered nodes for mergeMatching is
[Table 4.] Comparison of the number of buffered nodes for each query
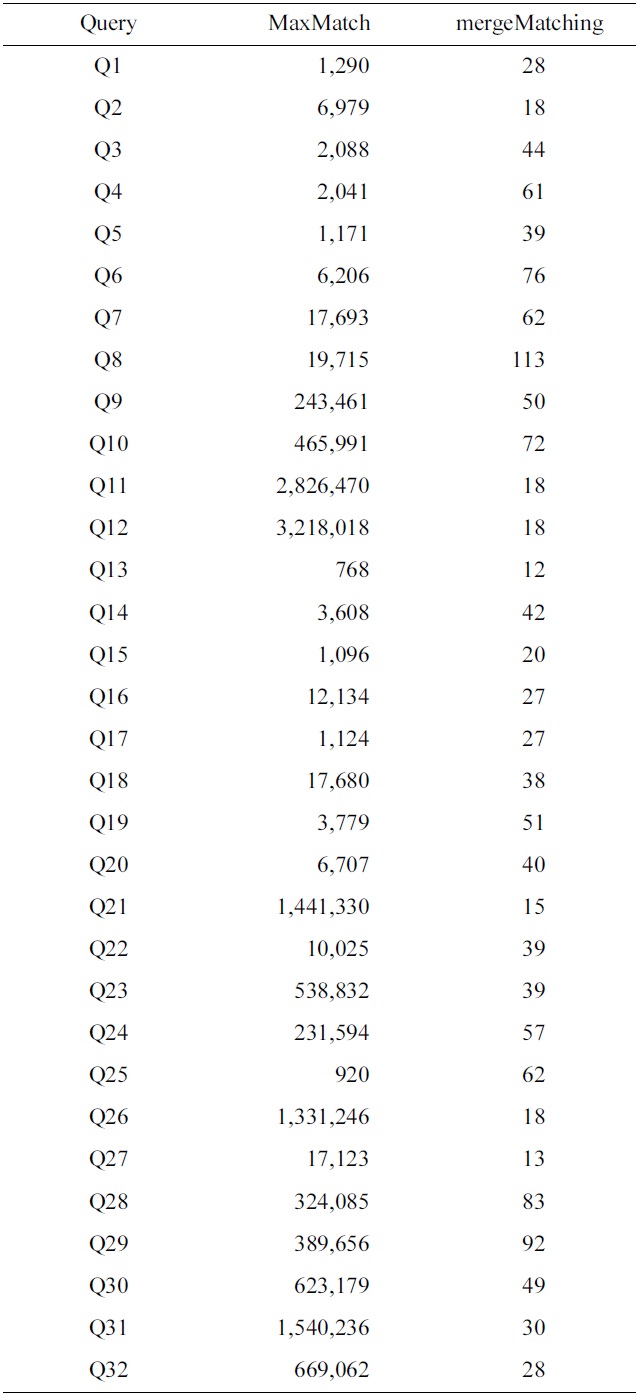
Comparison of the number of buffered nodes for each query
much less than that of MaxMatch. The reason lies in that MaxMatch needs to firstly construct
2) Comparison of SLCA Computation:
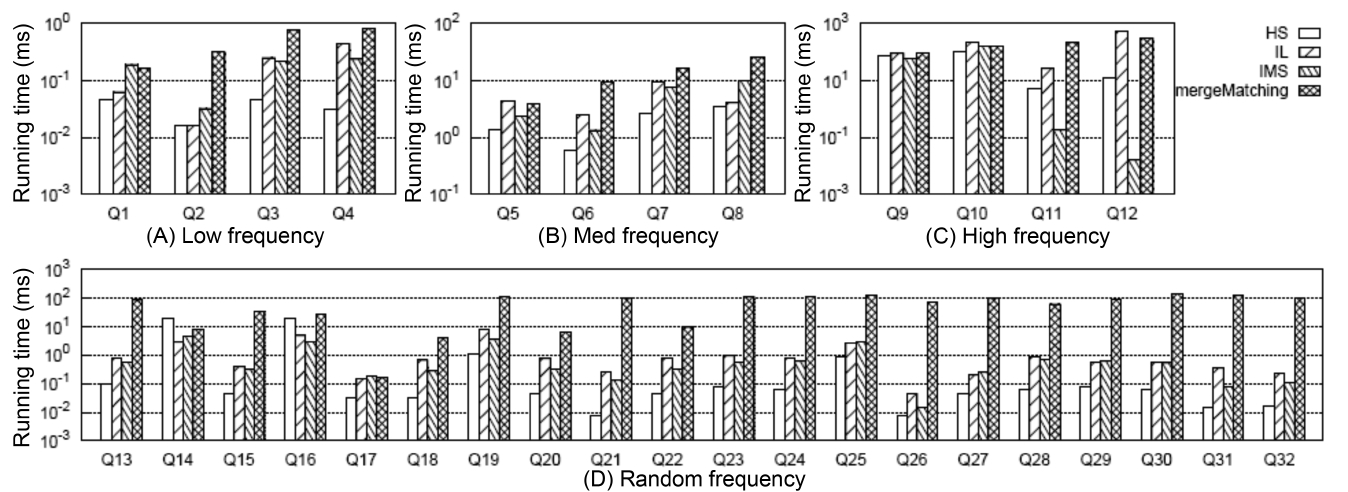
To get all matched subtree results, the first critical step is computing all qualified SLCA nodes. Fig. 4 shows the comparison of different algorithms on SLCA computation.
From Fig. 4 we have the following observations: 1) mergeMatching is beaten by HS, IL and IMS for almost all queries. This is because mergeMatching sequentially processes all involved Dewey labels. Its performance is dominated by the number of involved Dewey labels, while IL and IMS are more flexible in utilizing the positional relationship to prune useless keyword nodes; HS only sequentially processes each Dewey label of the shortest inverted Dewey label list
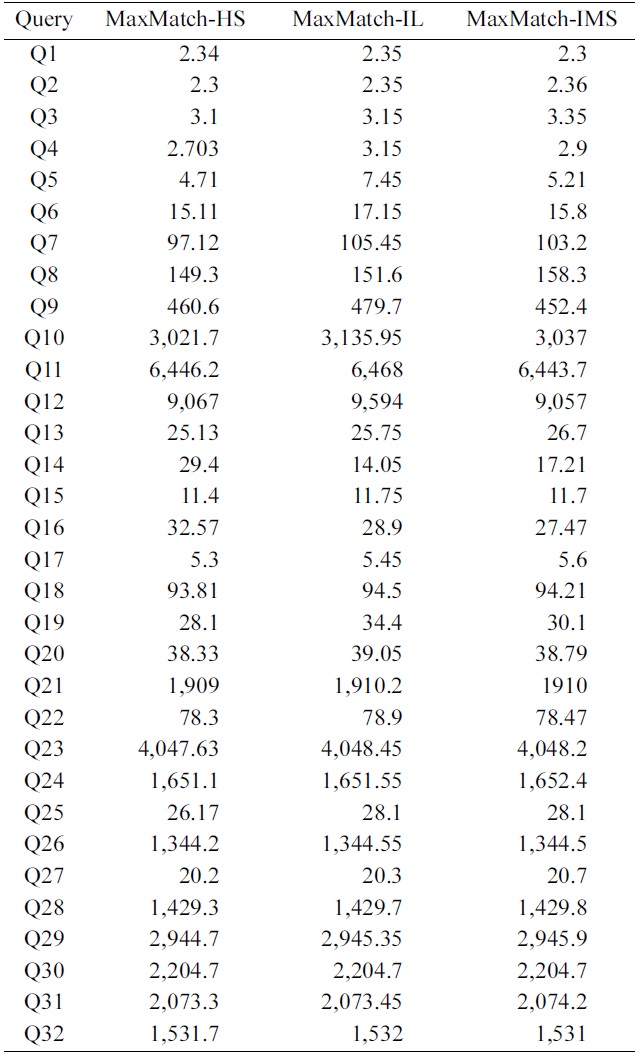
Comparison of the running time for the MaxMatch algorithm based of different methods on smallest lowest common ancesto computation (ms)
3) Impacts of the SLCA Computation on the Overall Performance
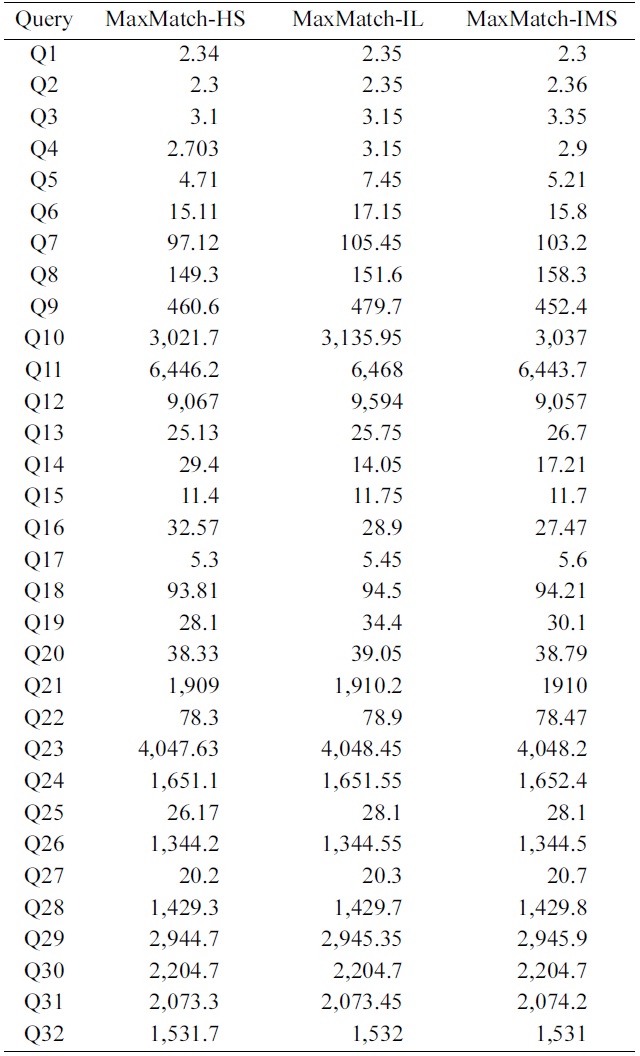
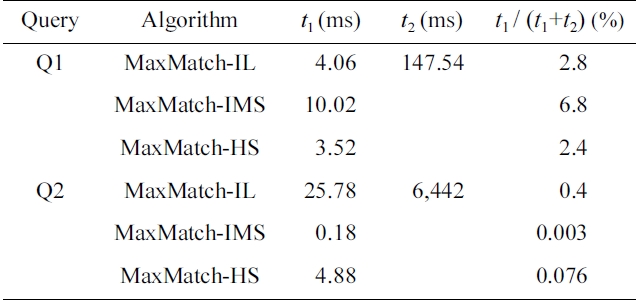
To further investigate the impacts of SLCA computation on the overall performance, we implemented the MaxMatch algorithm based on IL, IMS, and HS, which are denoted as MaxMatch-IL, MaxMatch-IMS, and Max- Match-HS, respectively. As shown in Table 5, the three algorithms always consume similar running time, and in most cases, MaxMatch-HS is a little better than the other two algorithms. The reason lies in that they all share the same procedure in constructing matched subtree results, which usually needs much more time than computing SLCA nodes. Therefore, even though HS performs better than IL and IMS in most cases, their overall performance is similar to each other.
Further, from Fig. 4 and Table 5 we know that no matter how efficient HS, IL, and IMS are, and no matter how much HS performs better than IL and IMS, or vice versa, their performance benefits on SLCA computation do not
exist anymore, if compared with the time on constructing matched subtree results based on the MaxMatch algorithm.
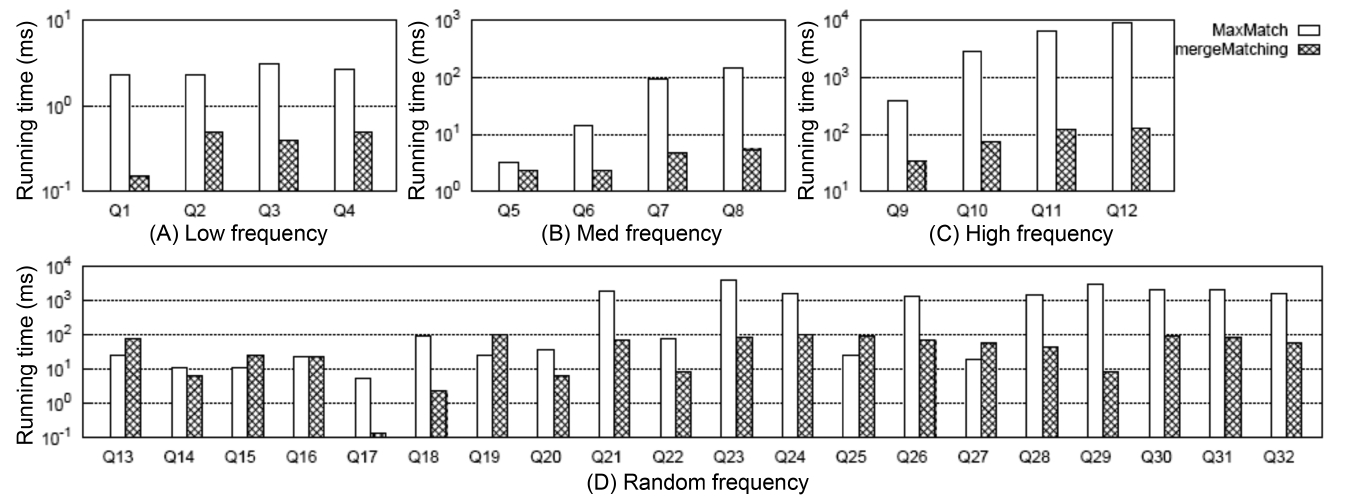
4) Comparison of Constructing Subtree Results
Fig. 5 shows the comparison between MaxMatch and mergeMatching on constructing all matched subtree results, from which we know that although mergeMatching is not as efficient as HS, IL, and IMS on SLCA computation, it is much more efficient than MaxMatch on constructing matched subtree results, such as Q1 to Q12, Q17, Q18, Q20 to Q24, Q26, and Q28 to Q32, and the time saved in the second phase is much more than that wasted in the first phase. The reason lies in that merge- Matching processes each Dewey label only once, while MaxMatch needs to firstly scan all Dewey labels once to compute SLCA results, then scan all Dewey labels once more to construct a set of initial groups according to different SLCA nodes. After that, it constructs all path subtree results by processing these Dewey labels again.
At last, it needs to traverse all nodes to prune useless nodes.
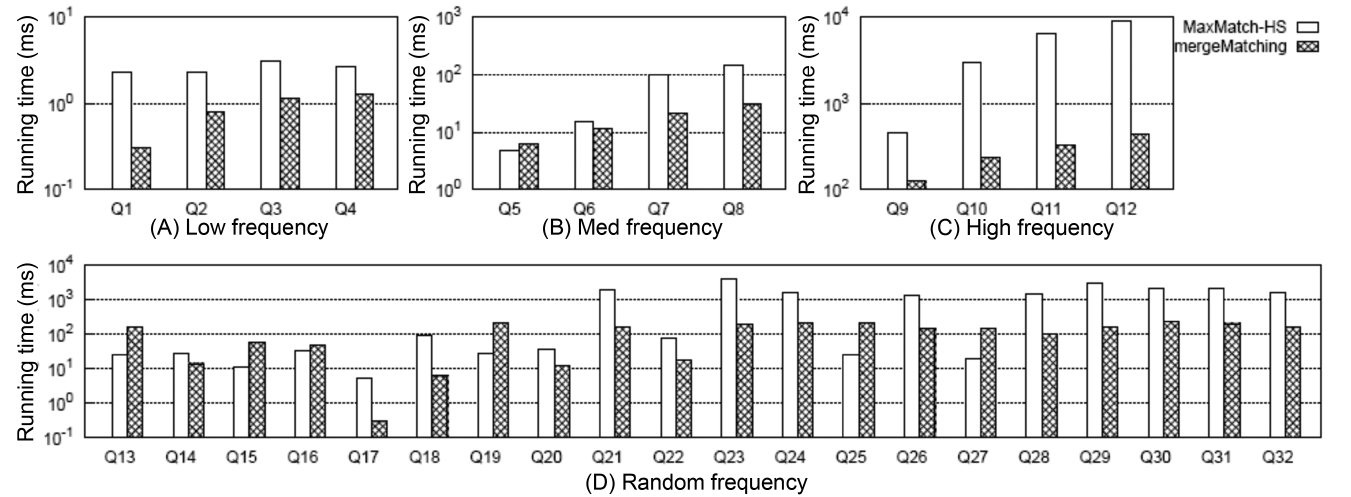
5) Comparison of the Overall Performance
Fig. 6 shows the comparison of the overall running time between MaxMatch-HS and mergeMatching, from which we know that in most cases, mergeMatching performs much better than MaxMatch-HS. The reason lies in that compared with MaxMatch, mergeMatching does not need to rescan all involved Dewey labels, and does not need to delay prune useless nodes after constructing all path subtree results.
On the contrary, it prunes useless nodes when constructing each matched subtree result, and thus can quickly reduce the number of testing operations of the keywords consumption relationship between sibling nodes.
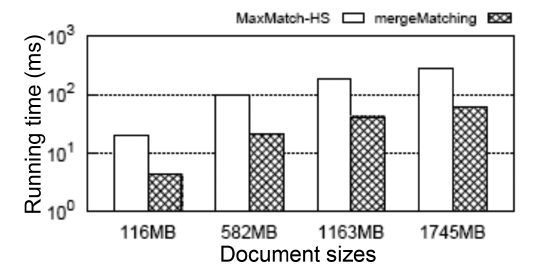
Besides, we show in Fig. 7 the scalability when executing Q7 on XMark datasets with different sizes (from 116 MB to 1745 MB [15x]). The query time of the MaxMatch- HS and our mergeMatching algorithms grow sublinearly with the increase of the data size. Also, mergeMatching consistently saves about 78% time when compared with MaxMatch-HS. For other queries, we have similar results, which are omitted due to limitations of space.
Considering that TMSubtree is more self-explanatory and compact than CSubtree and PSubtree, but existing methods on subtree result computation need to rescan all Dewey labels, we focus in this paper on efficient construction of TMSubtree results for keyword queries on XML data based on SLCA semantics. We firstly proved the upper bound for the size of a given TMSubtree, that is, it has at most 2