Continuous efforts to put the Semantic Web vision into practice have led to two important insights: implementing a full-fledged machine understandable Web has largely failed, but focusing only on the ‘reasonable’ part already reveals a vast variety of valuable data [1]. This area of socalled linked open data (LOD) [2] has immediately spawned interesting efforts, like the DBpedia knowledge base (http://www.dbpedia.org/About) that currently describes more than 3.64 million things, out of which 1.83 million are classified in a consistent ontology. Moreover, the potential applications also promoted the development of innovative methods to make such data available to users in a structured way. Information retrieval (IR)-style or rule-based extraction frameworks, like ALICE [3], Xlog [4], or SOFIE [5], can already crawl the Web, and extract structured relationships from unstructured data with largely sufficient accuracy.

However, when it comes to retrieval of the now struc-tured information, the typical query paradigms also have to be adapted. This is not only because extracted knowledge is usually represented in some form of knowledge representation language (with resource description framework [RDF] triples as the most prominent example), but also due to the semantic loss of focus that results from ambiguities in the extraction process. For instance when querying for a person’s place of birth, the information where somebody grew up is generally heavily related, but definitely less focused regarding the original query intention. Still, whenever the exact place of birth is unknown, the information where a person grew up is still much more helpful, than an empty result set. Thus, it should be retrieved as relevant, but of course should always get a penalty in the ranking. This desirable facet of retrieval is known as schema malleability [6,7].

While current retrieval paradigms, for example those in SOFIE’s retrieval engine NAGA [8] or Xlog’s DBLife [9], only focus on structured query language (SQL)-style retrieval (usually SPARQL over RDF) and keyword search with top-k ranking, the problem of preference-based retrieval paradigms, like skyline queries over linked open data, has not yet been solved. In this paper we tackle the problem of malleability-aware skyline queries over linked open data. The problem is twofold: first a viable semantics has to be defined, trading a user’s value preferences against the extracted relationships’ loss of focus with respect to the original query; then efficient algorithm(s) have to be designed, to solve the retrieval task in practical runtimes.

In a nutshell, the problem is the intuitive interleaving of each individual user’s attribute value preferences, with the generally applicable preferences on attribute semantics, as specified in the query. Whereas skyline queries up to now only dealt with relaxing value preferences, the new additional relaxation in attribute semantics is owed to the linked open data. Let’s extend our example from above:

Example: A user might be interested in famous Nobel laureates in physics who were born in Munich, Germany. Querying the DBpedia knowledgebase retrieves only two entries: Rudolf Mossbauer and Arno Allan Penzias. However, a similar query for Nobel laureates in physics growing up in Munich also retrieves Werner Heisenberg (who went to school in Munich); and a further relaxation to Nobel laureates in physics living in Munich finally retrieves Wilhelm Conrad Rontgen. With a different degree of relevance (with respect to famousness, and having a relationship with Munich) all these are possible answers that are, however, getting less focused with respect to the original query, and should thus be displayed accordingly. That means the final result, including schema malleability, may be a trade-off between the famousness of the physicists, and their relationship to Munich, which is best represented by a skyline query result.

To model this paradigm in databases (and schema malleability as such), each query attribute can be considered as a database column, holding not only tuples based on the strict relationships given by the query, but also tuples from semantic similar relationships. However, to prepare for later retrieval each such malleable attribute has to be associated with a second attribute measuring the semantic loss of focus for each tuple. This can be done by either automatically measuring semantic loss of focus by instance-based precision/recall tests, like shown in [10], testing the relationships’ semantic relatedness with externally available ontologies, like in [11], or simply denoting possible relationships, and allowing users to define a (partial) order over these relationships with respect to their queries.

In any case, the new associated attribute columns have to be considered by retrieval algorithms, but in contrast to the attribute value columns, have a slightly different quality. This is because relaxations on preferred values for cooperative query processing might change a tuple’s desirability, but larger relaxations in attribute senses might render tuples utterly useless. Consider the example above, where a Nobel laureate’s place of birth is relaxed in terms of the preferred value, e.g., from ‘Munich’ to ‘Bavaria’ or ‘Germany’, or in terms of the relationship with Munich, e.g., from ‘born in’ to ‘lived in’. Whether a broader relaxation of the sense like ‘visited’ is still of any use is doubtful. Thus, classical skyline query processing following Pareto-optimality cannot readily be applied. Moreover, by basically doubling the problem dimensionality also, the well-known efficiency problems of skyline processing in terms of runtimes and result set manageability, see for example [12], are bound to be encountered.

The contribution of this paper is threefold: we design an intuitive notion of skyline dominance with respect to malleability, in the form of semantically typed links in linked open data, and discuss its characteristics. We develop innovative algorithms to efficiently process skyline queries, even over large data repositories. And we extensively evaluate these algorithms with respect to runtime behavior and skyline manageability. In fact, our experiments show that in the general case, our algorithm can achieve significant performance improvements over the baseline. However, when slightly restricting general malleability, we can even show that performance can indeed be increased by several orders of magnitude, even rivaling the runtime behavior of classical skyline algorithms over strictly transitive preferences.

Please note that this paper is an extension of our work in [13]. Compared to [13], we heavily invest in generalized semantics for cases where non-malleable attributes show equivalent values. These semantics are discussed in Section IV-C and this new definition is also evaluated in Section V. This paper is structured as follows: after briefly surveying related work in Section II, we discuss the necessary foundations and theoretical characteristics of skylines over linked open data in Section III. Section IV then presents and evaluates skyline algorithms over several malleability attributes, whereas Section V deals with the special case of a single aggregated malleability attribute. We close with a short summary and outlook.

Due to its potential usefulness, linked open data has received a lot of attention, and even inspired a taskforce (http:// www.w3.org/wiki/SweoIG/TaskForces/CommunityProjects/ LinkingOpenData) of the World Wide Web Consortium (W3C). Current research is often focused on the area of business intelligence, but also for the collection of common knowledge. The basic idea is of using the Web to create typed links between data items from different sources. Once extracted, these links represent semantic relationships, which can in turn be exploited for querying. However, when querying (or reasoning over) such relationships, the exact nature of the relationship and its semantic correspondence to the query is often difficult. Therefore, apart from typical exact match queries (usually performed in SPARQL [http://www.w3.org/TR/rdfsparql- query/] over RDF triples), many approaches for ranking the best matching information have been designed.

The first notable approach to rank queries on extracted entity properties was Entity Search [14], proposing an elaborate ranking model that combines keywords and structured attributes. When it comes to also exploiting semantic relationships, NAGA [8] used a scoring model based on the principles of generative language models, from which measures such as confidence, informativeness, and compactness are derived, which are subsequently used to rank query results. Finally, [15] develops a general model for supporting approximate queries on graph-modeled data, with respect to both attribute values and semantic relationships, and derives a first top-k algorithm to implement the ranking efficiently. However, like in all top-k frameworks, even far-fetched semantic relationships can be compensated for, by good matching attribute values. Moreover, all these approaches directly work on graph-structured data relying on path-based semantic relatedness, e.g., as defined by [16], whereas our approach works on relationship malleability quantifying the respective loss of focus.

To our knowledge the only algorithm similar to skyline queries on linked open data is given by [17]. However, the developed algorithm has been designed for optimizing skyline queries over RDF data stored using a vertically partitioned schema model, and thus presents an efficient scheme to interleave the skyline operator with joins over multiple relational tables. Unfortunately, it does not offer any techniques with respect to personalization and the problem of semantic linkage, and thus is not really related to our work here. In brief, to our knowledge, our approach features the first skyline algorithm that respects semantic malleability.

In the following, we will briefly revisit the notion of Pareto skylines, as given by [18]. Assume a database relation R ⊆ D₁ × … × D_n on n attributes. 1) A preference P_i on some attribute A_i with domain D_i is a strict partial order over D_i. If some attribute value a ∈ D_i is preferred over another value b ∈ D_i, then (a,b) ∈ P_i, written as a >_i b (read “a dominates b with respect to P_i”). The set of all preferences is denoted as P. 2) Analogously, an equivalence relation on D_i compatible with P_i can also be defined. Then, two attribute values attribute a,b ∈ D_i can be defined as being equivalent with respect to the domain: a ？ _i b. Moreover, if some attribute value a ∈ D_i is either preferred over or equivalent to some value b ∈ D_i, we write

Assuming preferences P₁, …, P_n for each attribute in R, the concept of Pareto dominance between two tuples

can be defined as:

Definition 1: Pareto dominance

The classical skyline set [19] can now be defined as all those tuples in each database instance, which are not dominated by any other tuple:

Definition 2: Pareto skyline for some relation R and preferences P

Now we are ready to extend the semantics, by introducing the concept of malleability-aware dominance, which specifically respects the semantic challenges introduced by linked open data entities. As motivated above, the intuition is that regarding each queried attribute, personalized skyline queries consist of a user-specific value preference, and a certain meaning of the attribute that may more or less correspond to some number of extracted attribute types in the database instance. Thus, for getting acceptable results, not only the entities’ attribute values, but also the loss of focus with respect to each attribute’s semantics has to be taken into account. The baseline approach for this would be to simply compute skylines with a double dimensionality (one attribute value, and a malleability score for each attribute).

However, apart from the obvious scalability problems, the semantics are also unclear. Whereas attribute values, like dates, prices, or ratings, are usually crisp, and follow a certain preference order (users want the cheapest price for some product or the highest quality rating), labels for semantic relationships are usually fuzzy, and to some degree ambiguous, depending on their labels. Often grew_up_in maybe used synonymously with born_in, but lived_in definitely is not. Thus, the relative loss of focus (or d-distance) between semantic labels needs to be considered: if two labels differ at most by d, they should be considered semantically equivalent, but once two labels are too far apart, a different class of semantic relationship has to be assumed.

Definition 3: δ-preferences for modeling malleability over linked open data.

A δ-preference δP_i on some attribute A_i with metric domain D_i and metric dist_i(.,.) is a reflexive and transitive binary relation ？_i over D_i, together with an intransitive form of equivalence with the notion of indifference: for all a,b ∈ D_i: a ？_i b ⇔ dist_i(a,b) ≤ δ, see e.g., [20]. If some attribute value a ∈ D_i is preferred over another value b ∈ D_i and dist_i(a,b) > δ, we write a ？ _i b (read “a strictly δ-dominates b with respect to δP_i”). The combination of several δP_i can easily be achieved using the normal Pareto product and will be denoted as ？_δP. Likewise, we write a？_i b, if either a ？ _i b or a ？ _i b.

It is easy to mix δ-preferences and normal strict partial order preferences to create a product preference over some relation (which for ease of use we will again simply denote by ‘>’), and we will define the respective domination relationships for malleability-aware skylines in Sections IV and V. But up to now, such δ-preferences with relative distances have not been considered in skyline queries, because their use directly contradicts the generally assumed transitivity of domination relationships between tuples. Actually, results in psychology have long shown that, in contrast to common belief, intransitivity often occurs in a person’s system of values or preferences, potentially leading to unresolvable conflicts, see e.g., [21] or [22]. Analogously, in economics, intransitivity may occur in a consumer’s preferences. While this may lead to consumer behavior that does not conform to perfect economic rationality, in recent years economists have questioned whether violations of transitivity must necessarily lead to ‘irrational’ behavior, see for instance [23].

Indeed, from an order-theoretical point of view it is easy to show that whenever δ-distances are used in at least one preference, and

and

are given,

does not necessarily follow:

Lemma 1: Dominance relationships are not transitive using δ-distances.

Proof: Transitivity for dominance regarding any product preference P is violated, if three tuples

and

can be constructed, for which holds:

but

Assume a product preference P over some relation R, and assume there is one attribute m for which a δ-preference δP_m is declared, stating the equivalence of values within the relative distance of some fixed δ. Now define preference P^ by removing δP_m from P, and construct three tuples

and

such that

Now, assign values of

and

for attribute m as follows: y_m := (x_m + δ) and z_m := (y_m + δ).

Then, with respect to P,

holds because of

and x_m and y_m are equivalent with respect to the chosen δ. Analogously,

holds. However,

because of

but (z_m = (x_m + 2δ) ？ _δPm x_m). Hence

and

are incomparable with respect to P, and the domination relationship is not transitive.

□

While the resulting preference orders are not transitive, at the same time domination relationships within the intransitive product order are sensible, since there can never exist any cyclic base preferences. However, this is only the case when strict partial-order preferences and δ- preferences are used conjointly to build the product order; product orders built only from δ-preferences will inevitably lead to cycles. In order to guarantee a cyclic product orders, some observations can be made: 1) no cycles can ever emerge between tuples showing dominance with respect to any attributes, over which a strict partial-order preference is defined (due to their guaranteed transitivity), and 2) cycles can only occur, if tuples are equivalent with respect to all partial-order preferences. In this case, strict δ-dominance ( ？ ) must be enforced, and none of the tuples are allowed to dominate by simple δ-dominance alone ( ？ ). This leads to our formal definition of malleability-aware dominance (Definition 4) in Section IV-A.

The danger of intransitivity of dominance relationships is that it may lead to non-deterministic behavior when computing skylines using standard skyline algorithms. According to Definition 2, the skyline contains all tuples of a given relation that are not dominated by any other tuple, assuming that preferences are partial orders. Naively, this would need an algorithm pairwise comparing all tuples, with respect to the chosen dominance criterion. In practice, however, most skyline algorithms increase efficiency by pruning large numbers of tuple comparisons (e.g., basic block-nested-loop [BNL] algorithms [19], branch-and-bound algorithms [24], distributed algorithms [25], or online algorithms [26]). These optimizations usually all rely on the transitivity of dominance.

Example: When using non-transitive dominance with for instance a BNL algorithm, the result will vary nondeterministically depending on the order of the tuples in the database instance (and therefore, also the order of the tests for dominance). For example, when assuming

but

then a skyline computed by some BNL algorithm just contains

if the test for

is performed first, and thus

is immediately pruned from the database. Otherwise, if

is tested first, the resulting skyline contains

because

is removed prematurely, before

could also be removed by testing

and due to

incorrectly remains in the skyline set.

However, the idea of skylines is still sensible, since as we will prove in Lemma 2, cyclic preferences cannot occur, and thus a skyline based on the notion of containing all non-dominated objects can be computed. Since pruning may cause difficulties, the obvious way is by simply comparing all tuples in the database instance pairwise (with quadratic runtime). But, as we will see in the next section, far more efficient algorithms can be designed, and thus skylines over linked open data are indeed practical.

Before delving into designing skyline algorithms capable of dealing with intransitivity, as described above, we have to formalize our concept of product orders also built from d-preferences in the form of a dominance criterion usable in skyline algorithms.

Assuming preferences P that can be decomposed into strict partial-order preferences P^, and δ-preferences δP, the concept of malleability-aware dominance between two tuples

can be defined as:

Definition 4: Malleability-aware dominance over individual attributes

In this definition, there is a malleability-aware dominance: 1) if all non-malleable attribute values of

show Pareto dominance over

and all malleable attributes of

are at least equivalent to those of

with respect to the δ-preferences (i.e., all malleable attributes encoding the tuple’s loss-of-focus are tested for “soft” dominance here, allowing a certain δ of flexibility), or 2) if all data attributes are equivalent with respect to the Pareto preferences, but show strict dominance with respect to the malleable attributes for the δ-preferences (this means all malleable attributes encoding loss-of-focus have to show real Pareto dominance, i.e., no δ-distances are considered). This important property is required to prevent cycles to form in P:

Lemma 2: Product orders of strict partial order preferences and δ-preferences following Definition 4 cannot contain cyclic preferences.

Proof: We have to show that the dominance relation of the product order does not induce cycles, more precisely, if

with k > 1, then neither

nor

is possible. Please note that

means

for all non-malleable attributes and

for all malleable attributes, i.e., no malleability is allowed for equivalence.

For 1 ≤ t ≤ k let

where the first n attributes are non-malleable, and the following m attributes are malleable. We distinguish two cases: 1) There is a strict preference in the non-malleable part between two objects in an assumed cycle, i.e., there are 1 ≤ t < k and 1 ≤ i ≤ n such that x_t,i > _Pi x_t+1,i. Then, within the cycle we have:

and therefore x_1,i >_Pi x_k,i, rendering both

and

impossible; 2) If there is no strict preference in the nonmalleable part, for all 1 ≤ t < k and 1 ≤ i ≤ n we have x_t,i ？ _Pi x_t+1,i. Thus, following Definition 4 for the malleable attributes for all 1 ≤ t < k holds: (x_{t,n+ 1}, … , x_t,m) ？ _δP (x_{t+ 1},_{n+ 1}, … , x_t+1,m), which means (x_{1,n+ 1}, … , x_1,m) ？ _{δ P}. (x_{k,n+ 1}, … , x_k,m), due to the strictness of ？ _δP. Hence

is impossible. In the same way it is easy to also see that

is impossible.

□

Now, the respective malleability-aware skyline can be computed analogously to Definition 2, by:

Unfortunately, actually implementing such malleability- aware skyline computations algorithmically poses several challenges. Therefore, in the following we demonstrate how such algorithms can be designed. For the sake of cleaner notions and without loss of generality, we will assume that all our preferences are encoded in the database tuples by normalized scores in [0,1], where 1 represents the most preferable attribute values, and 0 the least preferable ones. Any database tuple

is given by

and the individual attributes can be separated into non-malleable data attributes x_i with i ∈ D (corresponding to P^), and malleable attributes x_i with i ∈ M (corresponding to δP). Then, the dominance criterion of Definition 4 can be re-formulated as:

It is easy to see that this definition is equivalent to the Pareto dominance, as given by Definition 1, for the cases of M = Ø or δ = 0. If M = Ø and δ > 0, then malleabilityaware dominance allows for additional tuples being dominated compared to Pareto dominance, hence the resulting Skyline is a subset of the Pareto skyline.

As already indicated in Section III-A, modern Skyline algorithms have come to rely on the transitivity of dominance criteria. For the sake of improved performance, many tuple comparisons are avoided by pruning objects early, relying on transitivity for computational correctness, i.e., a tuple shown to be dominated can be fully excluded from further execution of the algorithm. However, without guaranteed transitivity, even basic algorithms like the well-known BNL algorithm [19] fail. Therefore, the need arises to develop new algorithms that are able to cope with these new requirements. In this section, we will therefore present a general purpose algorithm designed for use with any non-transitive dominance criteria, including dominance for malleability-aware skylines.

The naive solution to the given problem is relying on exhaustive pairwise comparison, i.e., each possible tuple pair has to be tested for dominance. However, this algorithm shows prohibitive practical performance, requiring 1/2(n(n ？ 1)) expensive tests for dominance, with n being the size of the database (and assuming that each test for dominance is bi-directional, i.e., by testing a > _P b, we can test b > _P a at the same time).

Hence, we propose a novel algorithm, which is capable of dealing with any transitive or non-transitive preferences P. Our algorithm is derived from this naive implementation by carefully avoiding any tuples comparisons that are guaranteed to show no effect. This can be formalized as follows:

Given is a database relation R with n tuples and preferences P. Furthermore, we need the set T of all tuples which need further testing for 1) if any t ∈ T is dominated by any other tuple, and 2) if any t ∈ T dominates any tuples itself; T is initialized with T = R. Furthermore, we use the set S of all tuples that are the final skyline, and the set L (i.e., losers) of those tuples that have already been shown to be dominated by any other tuple. In contrast to Skyline algorithms with transitive dominance, we cannot exclude tuples in L from further computation without additional guarantees. This results in the following algorithm:

The algorithm contains two loops, the outer one iterating t over all objects to be tested that have not already been shown to be dominated. For finding new dominance relationships, the second loop iterates c over the set C (C is initialized in each run with T {t}.) By testing t and each c for dominance, objects can be marked to be dominated, by adding them to the set L of all losers. As soon as t is dominated, any subsequent comparisons of t with any other tuple that has been shown to be dominated can be avoided, as those yield no new information. If t was not dominated within the inner loop, it can safely be added to the skyline. Compared to the na?ve approach, this algorithm saves a significant number of superfluous tuple comparisons (see evaluation in the next section).

Furthermore, this algorithm can be efficiently implemented by representing the membership of a tuple in the different sets by simple flags attached to the tuples in R, thus minimizing the overhead of additional bookkeeping.

In the following, we will introduce a more general definition of malleability-aware skyline semantics, addressing some restrictions of the semantics introduced in Definition 4. Especially, we focus on the case that all non-malleable attributes are equivalent, i.e.,

For the case of equivalent data values, in our initial definition, we demanded strict dominance with respect to malleable attributes, in order to establish a dominance relationship between the two tuples. This constraint does not capture the intended semantics of malleable skylines perfectly, as it allows for no vagueness in the case of equivalent data values. However, Definition 4 represents a pragmatic restriction for the sake of simplicity, and guarantees the absence of cycles without any additional effort. For many datasets, i.e., especially those that have large, or even continuous domains for the non-malleable data attributes, this restriction has a negligible impact, as tuples with equivalent data attributes rarely occur. However, for tuples with smaller attribute domains, tuples equivalent with respect to data attributes may happen frequently, and thus, often, our malleable skyline heuristic does not trigger.

Therefore, the definition presented in the following will expand on this case, also allowing soft-dominance when non-malleable attributes are equivalent, but resulting in a more complex and computation-heavy definition. The effectiveness of this modification is highly dependent on the current dataset, and especially shines in scenarios where data equivalences can frequently occur― e.g., e-commerce datasets where product facts are automatically extracted from the Web, resulting in varying extraction quality (malleable attributes), and often colliding data values (as there is a common consensus among most manufacturers with respect to which product properties make sense and which don’t).

Let

where the first n attributes are non-malleable attributes respecting the partial- order preference P^, and the following m attributes are malleable with respect to a δ-preference δ P. Furthermore,

is defined analogously.

Then, similar to Definition 4, we can define general malleability-aware dominance between two tuples

as

Definition 5: Malleability-aware dominance over individual attributes

We will discuss the detailed semantics of this definition in the following:

Part (2) of Definition 5 is similar to Definition 4, and encodes the semantic that if all non-malleable attribute values of

show Pareto dominance over

and all malleable attributes of

are at least equivalent to those of

with respect to the δ-preferences, using “soft” dominance allows a certain δ of flexibility.

Also, the next two parts (3) and (4) also directly correspond to Definition 4. Please note that we changed the notation, in order to be consistent with the later components (5) and (6) of the definition, i.e., the expression

as used in Definition 4 is equivalent to

as used by (4) in Definition 5. Therefore, this part still means that if no soft δ-dominance on the malleable attributes with strictly dominating non-malleable attributes as given by (2) could be established, then we can establish dominance if all non-malleable data attributes are equivalent with respect to the Pareto preferences (3), and the malleable attributes are strictly better with respect to the δ-preferences (4).

The extension of Definition 5 over Definition 4 is in (5) and (6): here, an additional alternative option for establishing dominance is provided for the case that the non-malleable attributes are equivalent. Therefore, this new definition is more general, and it will usually result in more dominance relationships than the previous Definition 4, i.e., the resulting skyline is either equal, or a strict subset of a respective skyline, in accordance with Definition 4.

The semantics of (5) and (6) are that for the case

it is also possible to use soft-dominance on malleable attributes, as long as certain restrictions hold: especially, (5) encodes that tiny value variations within malleable attributes smaller than

are considered as just being noise, and only larger variations of x_i > y_i + δ

can lead to a dominance relationship between

and

Unfortunately, this change breaks the guaranteed absence of cycles, one of the major features of the original Definition 4. Therefore, further restrictions are needed, in order make use of both soft-dominance for malleable attributes, and cycle-free dominance relations. These restriction are given by (6), i.e., by the additional constraint

This constraint describes that in order for

to dominate

needs to be better in its sum over of its malleable attributes. This enforces a compensation mechanism, i.e., in order to dominate; a tuple

has to show at least one malleable attribute for which it is significantly better than the respective attribute in

and all other malleable attribute values that are worse in

than in

(but still below the noise level) need to be compensated for by the entirety of the tuple. Therefore, for example, dominance between an overall inferior tuple (but with all inferior malleable attribute values being below the noise threshold) showing just few better values is disallowed, unless the better values are significantly better, also compensating for the shortcomings of the other attributes. This eliminates the source for cyclic dominance relationships, rendering this definition safe.

In this section, we evaluate the effects of malleabilityaware dominance, respecting any number of malleable attributes on the properties of skylines. Furthermore, we will also measure the performance of respective skyline algorithms.

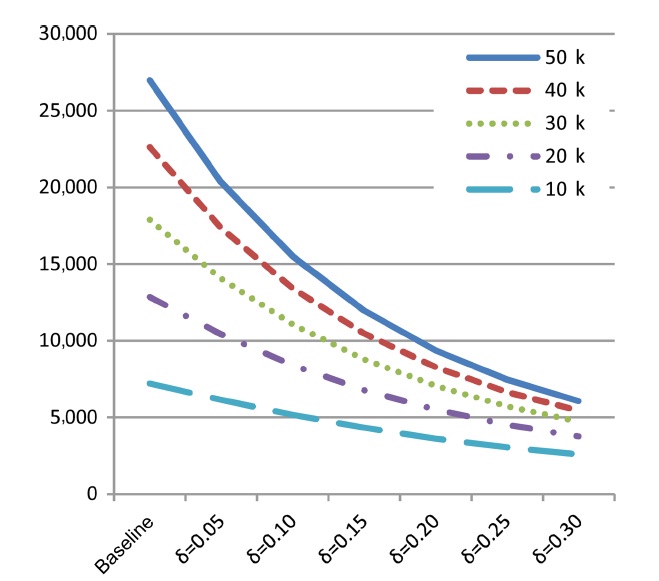
1) Skyline Size

For the first set of experiments, we examined the impact of malleability-aware dominance (represented by varying values δ) on the skyline size. For this purpose, we relied on synthetic data, and in each experimental run generated new database tuples with 12 independently distributed numeric attributes. Six of these attributes represent non-malleable (data) attributes, while the other six attributes are malleable ones, representing loss-of-focus. Using the operationalized dominance criterion of Section IV-A, skylines are computed for d-values ranging from δ = 0 (the baseline; equivalent to Pareto skylines as in Definition 2) to δ = 0.3. For each value of d, the experiment is repeated 50 times with newly generated tuples (to

ensure comparability, the same random seed is used for each δ, resulting in the same sequence of generated tuples). The averaged results are shown in . It is clearly obvious that the skyline resulting from the baseline (δ = 0, identical to the Pareto skyline of the same data) is not practically manageable: from the 50,000 database tuples, 26,981 are contained in the skyline (53%). This can be attributed to the high dimensionally of d = 12. But with growing δ, the skyline sizes dramatically decrease: already with δ = 0.15, the skyline is reduced to 11,959 tuples on average - a clearly more manageable result. Similar behavior can also be observed for smaller database sizes. Therefore, we can conclude that the malleability- aware skyline indeed efficiently addresses the issue of overly large skylines, when considering malleable lossof- focus attribute per data attribute.

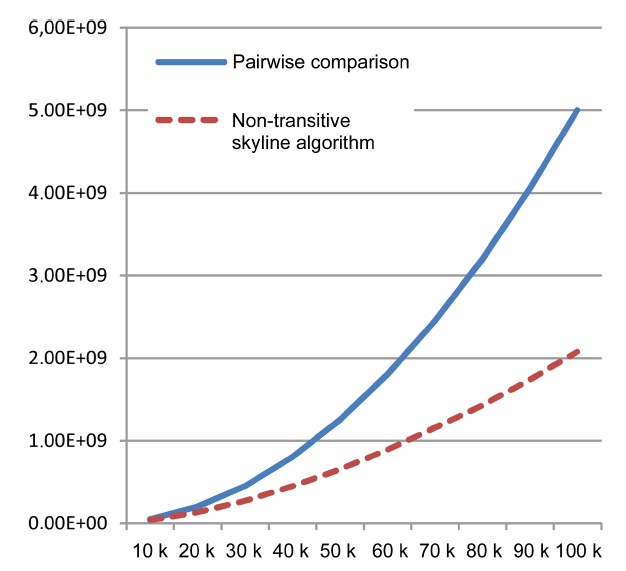
2) Performance of Algorithms

In the second set of experiments, we examined the performance of the naive baseline and our non-transitive skyline algorithm (measured in the required number of tests for dominance). Similar to the last experiment, we again relied on synthetic data with 12 independentattributes (6 malleable, 6 non-malleable), and incrementally increased the size n of the database from 10,000 tuples up to 100,000 tuples. The results are shown in Fig. 2: clearly, our non-transitive algorithm shows significantly better performance than the baseline, using pairwise comparisons. Furthermore, this performance advantage increases with growing database sizes. But still, the total time required by both algorithms is quite high (272 seconds with n = 100 k using our non-transitive skyline algorithm vs. 637 seconds for pairwise comparisons; tests performed on a 1.86 GHz Dual-Core CPU, using Java 6

and just a single core.) Therefore, additional optimizations must be found for application domains with tighter time constraints.

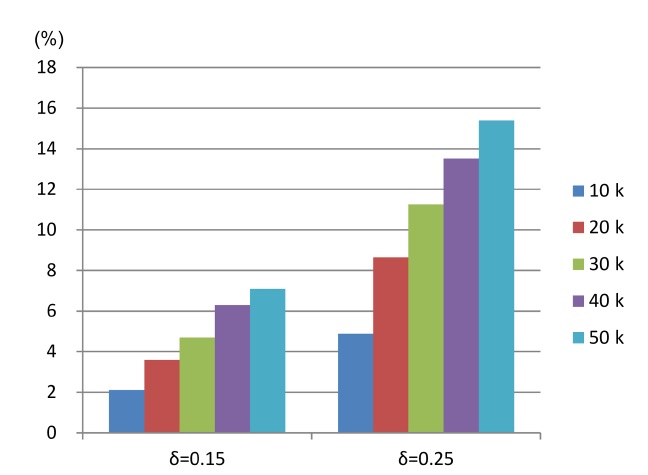
In this section, we briefly demonstrate the effect on the skyline size of the alternative Definition 5 for malleable skylines, given in Section IV-C, over the original Definition 4, given in Section IV-A. As this definition specifically extends Definition 4 with respect to equivalent (nonmalleable) data values, this experiment uses slightly different data sets, encouraging the occurrence of such tuples (i.e., showing equivalent non-malleable parts). This is achieved by generating discrete data values with 10 levels, e.g., possible values are 0.0, 0.1, …, 0.9. Furthermore, we only use 5 non-malleable attributes and 5 malleable ones, for a total of 10 attributes. Skylines computed using definition 5 are, as mentioned in Section IV-C, a subset of skylines computed with Definition 4, i.e., Definition 5 may result in additional domination relationships under certain conditions (simplified: when non-malleable attributes between two tuples are equivalent, and the malleable attributes are not strictly dominating, but most non-malleable attributes are roughly similar, with some attribute values being significantly better for one tuple).

In brief, in this experiment, we measure the relative skyline size reduction when comparing skylines computed with Definitions 4 and 5. For δ = 0.0, both definitions obviously behave similarly. Furthermore, as we use discrete values with distances of 0.1, Definition 5 behaves similarly for groups of δ -values δ ∈ {0.0, 0.05, 0.1}, δ ∈

{0.15, 0.2}, and δ ∈ {0.25, 0.3}. Therefore, the results shown in Fig. 3 are for relations with 10 k to 50 k tuples, and δ -values δ = 0.15 and δ = 0.25. It can be clearly seen that the effectiveness of the heuristic increases with increasing database size, as due to our experimental setting, the probability of tuples fulfilling the conditions required for the extensions provided in Definition 5 also increases. On an absolute scale, for the example of 50 k tuples generated as described above, the skyline is 4,567 tuples for δ = 0.0. For δ = 0.15, Definition 4 results in 1,594 tuples, while 5 results in 1,481 tuples, leading to the 7% relative reduction depicted in the figure. For δ = 0.25, the skyline sizes are 630 vs. 533 tuples. Overall, we can see from this evaluation that our alternative Definition 5 is beneficial, for the case of datasets with frequently occurring equivalence between tuples, with respect to the non-malleable attributes. However, it is very domain dependent if data does indeed show this property or not (for further illustration: if the same experiment is run using randomly generated non-discreet float values in [0,1], the effect of the definition is barely visible, and relative reductions are usually below 1%).

As demonstrated in the last section, the runtime of general non-transitive skyline algorithms with one malleable loss-of-focus attribute for each non-malleable data attribute can be quite high. Thus, for time-critical applications, we suggest reducing the number of malleable attributes to using just a single attribute. This single attribute then represents the overall loss-of-focus of a given database tuple with respect to the query, in an aggregated form. This reduction can be implemented by different methods: 1) by combining multiple malleable attributes by some combining function, or 2) by directly eliciting just a single attribute representing loss-of-focus, using one of the established frameworks for this task (e.g., [10] or [11]).

As an immediate effect, the number of dimensions to be respected during skyline computation is reduced drastically, leading to direct performance advantages, due to respectively reduced skyline sizes. However, there is a less obvious and significantly more crucial advantage resulting from this reduction, which allows us to build vastly more efficient skyline algorithms. The basic considerations leading to these algorithms are as follows:

When using established skyline algorithms, like BNL, the only problem which is encountered when dealing with malleability-aware dominance is that tuples are eliminated early that are required to dominate another non-skyline tuple, and due to non-transitivity, none of the remaining tuples can lead to the same dominance; thus an incorrect skyline is computed (e.g., see example in Section III-A). Therefore, we could use a more efficient standard algorithm, like BNL, if it could be made “safe”, i.e., if this situation can be prevented. In the general case with multiple malleable attributes, this is unfortunately not possible. But when using just one malleable attribute, the correctness of BNL depends only on the order in which the tuples are inserted into the window: for example, consider three tuples with preferences already encoded in scores

and

the bold score represents the single malleable attribute. When computing a malleability-aware skyline with δ = 0.20, then

and the resulting skyline is just

But due to

the BNL algorithm could first test

removing

and resulting in the skyline

(because

cannot be dominated anymore). Obviously, the skyline result would be correct, if the tested order was

It is easy to see that this observation can be generalized, i.e., problems in BNL can only occur if tuples with a lower malleability score are removed before they have been tested for dominance against all tuples with a higher malleability score. Therefore, for the case that there is only one malleable attribute, we can use established algorithms like BNL, if all tuples are processed in descending order with respect to the malleability attribute (preventing the situation leading to incorrect skylines described above), i.e., the skyline algorithm is therefore stratified with respect to the malleability attribute. This can be implemented by presorting the data before executing e.g., by a BNL algorithm. The effectiveness of this approach is tested later in this section.

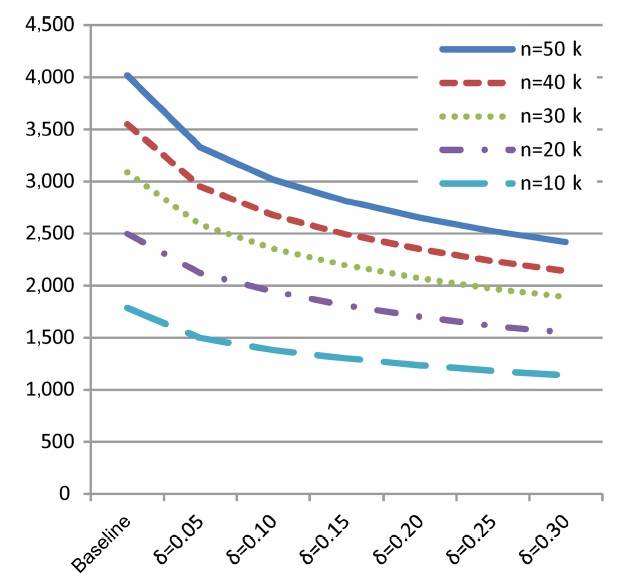
1) Skyline Size

Before dealing with performance issues, similar to the last section, we also measured the skyline sizes for varying δ and database sizes n. Again, we generate tuples using 6 non-malleable independently distributed attributes, but just one single malleable attribute. As now the number of overall dimensions is reduced from d = 12 down to

d = 7, the respective skyline sizes are also reduced dramatically to only 4,017 tuples (8% of database) for the baseline δ = 0 with n = 50,000 (see Fig. 5). But still, by slightly increasing δ , the skyline can be furthermore decreased to more manageable levels (e.g., 2,809 for δ = 0.15 and n = 50,000).

2) Performance of Algorithms

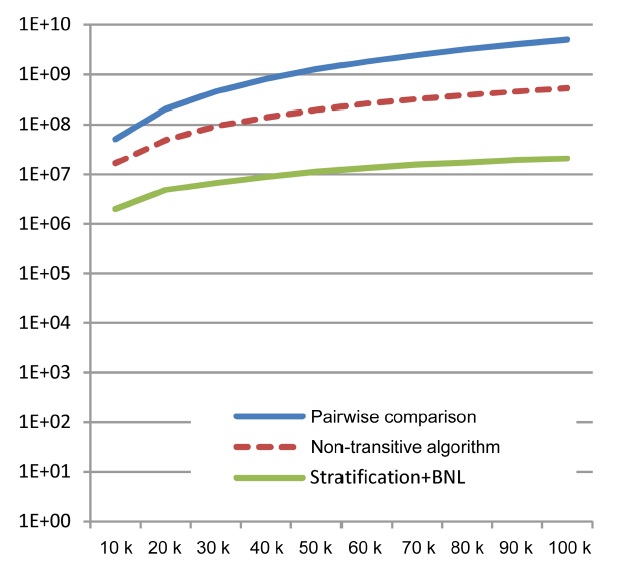
In this last set of experiments, we examined the performance of the naive baseline, our non-transitive skyline algorithm, and the stratified BNL algorithm as described above. Again, performance is measured by the required number of tests for dominance. We also relied on synthetic data with 7 independent-attributes (one malleable, 6 non-malleable), and incrementally increased the size n of the database from 10,000 tuples up to 100,000 tuples. The results are shown in Fig. 5 (using a logarithmic yaxis). Here, we can see that the stratified BNL-algorithm needs roughly two orders of magnitudes fewer dominance tests than the na?ve baseline, and is also one order of magnitude more efficient than our general non-transitive skyline algorithm. In terms of absolute runtime, the general non-transitive algorithm needed 218 seconds for n = 100 and δ = 0.15, which is still quite long. In contrast, the stratified BNL algorithm could be executed in less than 1.4 seconds using the same hardware (the time needed for sorting the 50,000 tuples before executing the algorithm is negligible). This significant result clearly shows that malleability-aware skylines can even be used in interactive environments having tight constraints with respect to response time, such as web applications.

In this paper we discussed the case of query processing over LOD. Whereas traditional query processing algorithms are usually graph-based, and use exact matches on typed links between data items in SQL-like languages like SPARQL, the fuzzy nature of semantic links calls for approximate query processing algorithms. In particular, the exact labels of links cannot always be taken at face value, because information extraction techniques, the use of different concept ontologies, and slight variations in the links’ semantics introduce quite a bit of fuzziness, which algorithms have to deal with. Relying on techniques to estimate different labels’ loss of focus regarding each other, in this paper we presented the first skyline query algorithm that can efficiently deal with semantically typed links in linked open data. Modeling the semantic malleability of attributes by d-preferences, we proved that the resulting product order is indeed well defined, and can be used effectively as the basis for a sensible definition of malleability-aware skylines over linked open data.

Moreover, in our experiments we show that our innovative algorithms can efficiently evaluate such skylines, and when restricting the type of malleability, will even result in runtime improvements of several orders of magnitude against the baseline. Therefore, even interactive applications with tight response time requirements are possible. While we performed the algorithmic considerations here on synthetic data to test our algorithms in an unbiased environment, our future work will focus on the integration of our algorithmic framework into practical LOD sets. Our aim is to use potential bias in the data for a tighter integration of the attribute malleability, respective to each individual query. It seems that different query intentions might need different degrees of admissible malleability, to stay semantically meaningful.