Ultraviolet (UV), visible, and near infrared (NIR) light have been extensively used in therapeutic and diagnostic modalities [1-3]. However, the depth of light penetration is still limited to a few centimeters because of the light scattering property of tissue, resulting in low photon densities.

Various methods such as increasing the power and diameter of the incident beam [3-5], application of optical clearing agents [6,7], and skin compression [8-10] have been suggested to increase the photon density in tissues. In a previous study, we developed a compression-controlled low-level laser probe (CCLLP) to increase the photon density in tissues by applying negative compression [11]. Figure 1 represents the CCLLP, which consists of a vacuum hole to supply negative compression, a hollow brace for guiding and supporting the optical fiber, and an acrylic probe body to maintain the negative compression applied to the tissue. We experimentally validated the efficacy of the CCLLP by measuring the photon density in ex vivo porcine skin samples [11].

In another previous study, we mathematically modeled and simulated the effects of tissue compression [10]. We simulated tissue compression in two ways: (1) non-uniform skin deformation with constant optical coefficients and (2) uniform skin deformation with variable optical coefficients depending on changes in skin thickness. However, neither of these approaches accurately simulated the mechanism of the CCLLP.

Although several numerical simulations for non-flat boundaries or layers have been reported [12,13], the geometry

of the outer boundaries and inner layers similar to the skin affected by the CCLLP has not been described. The skin region affected by the CCLLP swells outward except for the area under the optical fiber probe. In the previous uniform compression study [10], the photon density did not increase in the swollen areas but increased in the region of skin under the optical fiber probe. In this study, which is a fundamental generalization of the simulation reported in [10], we numerically simulated such competing effects between the swollen and compressed regions in the CCLLP.

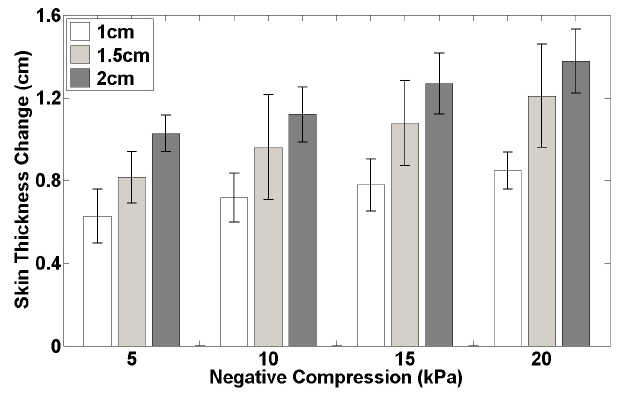
In three subjects, we experimentally measured the change in skin thickness due to negative compression and used the values for the numerical simulations. We represented the deformation of the skin surface associated with the CCLLP using three quadratic Bezier curves. We also numerically modeled the changes in optical coefficients with changes in skin thickness using a linearization method. We obtained simulation results as functions of the modeling parameters, radius of the CCLLP, and negative compression, and compared these with results from an ex vivo experiment using a scaling factor.

The photon density in tissues was modeled using the radiative transfer equation or its diffusion approximation [14]. The diffusion approximation in the frequency domain was represented by the following elliptic partial differential equation in the region of interest Ω :

where r₀ is some point on the boundary of Ω . For the notations used in the equations, see the Nomenclature section before the Reference section at the end of this paper.

To solve (1) using the finite element method (FEM), the geometrical domain Ω was assumed to be bounded, and appropriate boundary conditions were assigned to the boundary ∂ Ω . Let us assume that Ω = [-w, w] × [-d, 0]. That is to say, the region of interest is a rectangular region in the two-dimensional xz plane modeling a few skin layers with depth d, deposited in the direction of the z-axis. Then ∂ Ω is composed of four straight lines:

∂top Ω =[-w, w]×{0}: the top of the skin contacting the air

∂bottom Ω =[-w, w]×{-d}: the bottom of the skin region of interest

∂left Ω ={-w}×{-d,0}: the left of the skin region of interest

∂right Ω ={-w}×{d,0}: the right of the skin region of interest

Note that only ∂^top Ω contacts air, while the other boundaries contact skin. Thus, we imposed the Neumann boundary condition on ∂^left Ω , ∂^right Ω , and ∂^bottom Ω and the Robin boundary condition on ∂^top Ω to reflect differences in refractive index mismatching [14]. Therefore, we obtained the following boundary value problem for modeling light propagation in skin:

Let us divide Ω into small triangles or rectangles, which are called finite elements, and {u_i}_i=1,…Nb be the corresponding finite element bases spanning piecewise-linear or -bilinear function spaces. The finite element formulation for (1) with the boundary condition (2) using the finite element bases is then given as follows:

The finite element solution for (3) was found using COMSOL 3.4 (COMSOL AB, Stockholm, Sweden). In the simulation, the photon density, or light fluence rate, was measured at the bottom ∂^bottomΩ of the domain of interest and at a distance 7.5 cm away. However, we could neglect the 7.5 cm distance in the air for the photon density measurement since light is mostly absorbed and scattered in the tissue rather than in the air.

The optical properties of human tissues have been reported in several studies [3,15]. Based on these studies, a five-layer skin model was used for a 633 nm light [3].

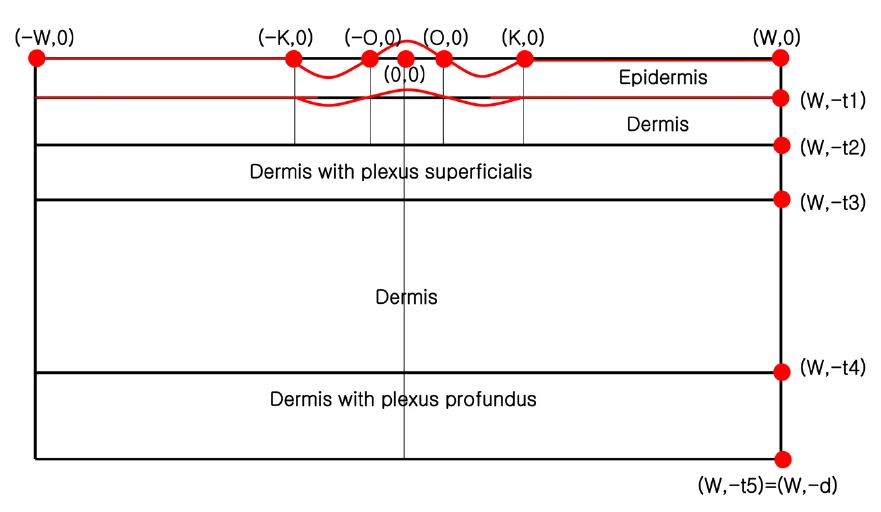
For simplicity, we modeled the domain of interest Ω in two dimensions by neglecting the y-axis. When there is no compression, Ω is given as follows:

where Ω_i and di are the domain of interest and the thickness of the i-th skin layer, respectively, dx is the dimension of the skin layer along the x-axis, and t₅ = d. The thicknesses of layers d_i(i = 1,2,3,4,5) are presented in Table 1 with their optical coefficients. The overall five-layer structure is depicted in Figure 2.

We then formulated the layers Ω_i(i = 1,2,3,4,5) with negative compression. Let 2K and 2O be the length of the region contacting the entire acrylic probe body of the CCLLP and

the length of the region contacting the guide for the optical fiber, respectively. Let C be the midpoint between K and O. If negative compression is applied throughout the regions [-K, -O] and [O, K ] on the skin surface, these regions become swollen by the maximum height difference shown in Figure 3 for the applied negative compression. On the other hand, in the region [-O, O], the skin surface should be retracted between the points (-O, 0) and (O, 0) because of the swollen surfaces surrounding it. For more detailed evaluations, elastic or visco-elastic analysis could be used [16,17]; however, in this study, we used three quadratic Bezier curves for the regions [-K, -O], [-O, O], and [O, K]. The data shown in Figure 4 were used as the maxima of the two Bezier curves for [-K, -O] and [O, K], and the Bezier curve for [-O, O] was constructed to join the three curves without any discontinuity of tangential lines. Let l_i be the upper surface of i-th layer (i = 1,2,3,4,5), which is a straight line before the application of negative compression. For this purpose, control points were chosen as follows:

where C was chosen as K + O/2 to cause the two Bezier curves for [-K, -O] and [O, K ] to be symmetric; S = 2O/(K - O) was chosen so that the three Bezier curves joined without any discontinuity of tangent lines, especially at -O and O; and si(i = 1,2,3,4,5) is the maximum skin surface change for i-th layer. We chose w = 3.5 cm, K = 2 cm, and O = 0.2 cm, based on the sizes of the skin sample and CCLLP.

Using the definition of a quadratic Bezier curve, we obtained the following detailed representations for l_i, i = 1,2,3,4,5:

Therefore, the thicknesess of the i layers are as follows:

Assuming the thickness changes for the third, fourth, and fifth layers are relatively small and the change for second layer is half of the change in the first layer, we let

s₃ = s₄ = s₅ = 0 and

In the CCLLP, negative compression is applied to the skin surrounding the central area [？O,？K]×{0}？[K,O]×{0} in contact with the probe, and positive compression is applied at the center [?K,K]×{0} due to skin tension. The change in optical coefficients with uniform and partial compression of the skin was previously studied and reported [10]. Let

and

μ_a, μ_s'

be the optical coefficients for the i-th layer (i = 1,2) when the thickness of the layer is d_i and

respectively. Using an analysis similar to that in [10], we assumed that the relationship between the thickness and the absorption coefficient is:

The coefficient α is the optical modeling coefficient between 0 and 1, which related the reduction of skin penetration depth to the increase of optical coefficients. The more fundamental meaning of the coefficient is discussed in the “Discussion” section.

Equation (8) is linearly approximated as follows:

Similarly, we obtained the following relationship between the thickness and the reduced scattering coefficient:

Given that the diffusion coefficient is defined as a constant multiplied by the reciprocal of the sum of the absorption and reduced scattering coefficients, using (9) and (10) we obtained:

In (9), (10), and (11), we used first-order Taylor series approximations.

Using (7) and (11), we obtained an explicit representation of the diffusion coefficient as follows:

We chose the value for s1 based on the data shown in Figure 4, and si(i = 1,2,3,4,5) were chosen such that

decreased with the ratio of the depth from the surface to the entire depth of the skin. Thus, (12) becomes:

and (9) becomes:

Figure 1 shows CCLLPs with radii of 1, 1.5, and 2 cm. In Figure 3, Skin deformation by negative compression was investigated in the left arms of three subjects. Figure 4 shows the change in skin thickness averaged across the three subjects during negative compression as a function of the radius of the CCLLP. As described in the section II.1, the change in skin thickness was modeled using three Bezier curves with continuous tangential lines.

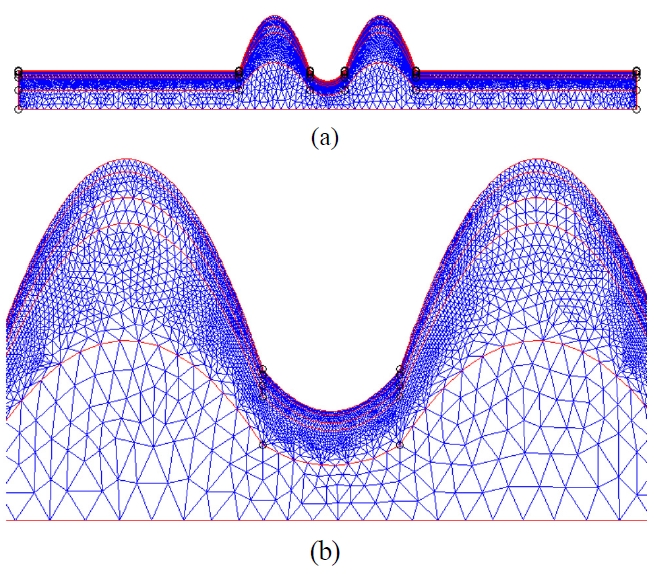
For the FEM analysis of the CCLLP, a finite element mesh was applied to the modeled geometry of the skin. We used meshes shown in Figure 5 for the skin deformation geometry to obtain the photon density distribution by FEM. The mesh is finer in the upper layers and coarser in the lower layers because skin deformation is expected to be less pronounced in the lower layers.

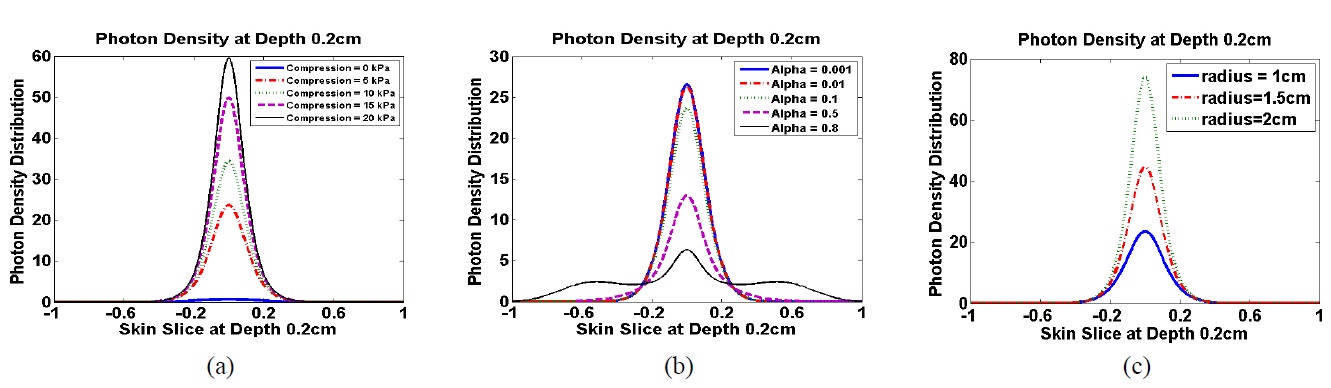
The optical coefficients for the five layers used in modeling the skin structure are shown in Table 1 [3]. The resulting photon density distributions at a depth of 0.2 cm below the skin surface are presented in Figure 6 as functions of negative compression, the thickness-coefficient

relation parameter α which is represented in (8), and the radius of the CCLLP.

In our previous study [11], we investigated the efficacy of CCLLP by measuring the photon density distribution in ex vivo porcine samples. In Figure 7, the photon density ratio, which is defined as the ratio of the photon density distribution between a given negative compression and no compression, was compared to the experimental data for a CCLLP with a radius of 1 cm. To compare the results of this study with the ex vivo data, the maximum change in skin thickness in vivo for human subjects was halved in the numerical simulation. The experimental and simulation results for various values of α (0.5,0.6,0.7, and 0.8) was shown in Figure 7.

The photon density in the tissue due to negative compression was influenced by two successive and competing physical phenomena: (1) the change in skin thickness due to compression and (2) the change in optical coefficients due to the change in skin thickness. In previous studies, the correlation between the change in skin thickness and negative compression was mathematically modeled using elastic equations [18,19]. In this study, the correlation was experimentally obtained from three subjects, and the data (Figure 4) was used to mathematically simulate the mechanism of the CCLLP. The changes in skin thickness for all three subjects were approximately proportional to the logarithm of the negative compression, which corresponds well with the results of previous studies [18,19].

Skin surface deformation by the CCLLP was experi

mentally measured as a function of negative compression (Figure 3). The region of skin contacting the optical fiber probe was compressed for two reasons: (1) this region of the skin was pressed down and thus could not swell up, and (2) the skin in the contacted region was pushed aside to the surrounding region, which swells outward. In other words, the skin inside the CCLLP, except for that in contact with the optical fiber probe, swells outward, whereas the contacted region is compressed inward. Thus, the skin surface can be modeled by: (1) two straight lines representing the two flat areas of skin outside the CCLLP, (2) two concave Bezier curves representing the raised skin region inside the CCLLP not contacting the optical fiber probe, and (3) one convex Bezier curve representing the compressed skin region contacting the optical fiber probe. The two concave Bezier curves and the convex Bezier curve were constructed to satisfy the C1 assumption at the two points where the curves meet, representing the boundary of the optical fiber probe. The C1 assumption states that the tangential lines representing the skin surface, as well as the skin surface itself, are continuously connected across the optical fiber probe inside the CCLLP. In other words, the skin surface deformation due to negative compression should be smooth and not have any discontinuities along the skin surface. The resulting skin surface deformation was shown in Figure 5.

The optical coefficients are known to be inversely proportional to skin penetration depth [8,9]. However, the relationship has been experimentally investigated with only a limited number of samples and is not well established for human or animal skin samples. Therefore, the relationship was mathematically modeled [10] when uniform compression was applied to the skin surface, corresponding to α = 0.5 in (8). Analysis of the changes in the optical coefficients with skin thickness was generalized from a uniform geometry [18] to a more complex geometry (Figure 5). Detailed changes in the optical coefficients with the generalized parameter α were computed using (13) and (14).

The skin thickness at the center decreased because of negative compression, resulting in increased photon density. At the same time, by the result of [8,9,10], we assumed that the optical coefficients (including the absorption coefficient (8),(9), the reduced scattering coefficient (10), and the diffusion coefficient (11)) per unit skin penetration depth increased through the optical modeling coefficient α as the skin thickness decreased, and thus interfered with the increase in photon density. Previous experimental [8,9] and simulation [10] results have shown that the increase in photon density due to the reduction in skin thickness is greater than the decrease due to changes in optical coefficients. However, this study modeled a more complicated phenomenon than the uniform compression case. In the skin deformation model, the skin regions inside the CCLLP and those contacting the optical fiber probe are raised and compressed, respectively. Therefore, the effects of skin deformation on photon density in these two regions are in opposite directions. A previous study using ex vivo porcine samples [11] presented the efficacy of the CCLLP in enhancing photon density. These results were verified by numerical simulation results (Figure 6) which used data on in vivo changes in human skin thickness. From these results, we conclude that the decrease in skin thickness directly under the optical fiber probe is more important than the increase in skin thickness in the surrounding areas. In addition, the negative compression, value for α , and radius of the CCLLP in the present results were all larger than in the previous study.

The peak intensities of photons in the ex vivo porcine samples [11] were compared with the simulated results. Changes in skin thickness were not obtained in the previous study because of the instability of the physical state of the ex vivo porcine skin samples. Therefore, skin deformation was measured in the arms of three human subjects, and changes in the skin thickness were halved to enable comparisons with the ex vivo porcine skin samples.

The CCLLP was developed to increase the photon density in tissues by applying negative compression. Skin deformation due to the CCLLP was numerically modeled using three Bezier curves. The finite element simulation used experimental data on changes in skin thickness from three human subjects, skin deformation modeling, and changes in optical coefficients as a function of the optical modeling coefficient α . The photon density increased when the negative compression and radius of the CCLLP increased. The simulated results at various values of α were similar to the ex vivo experimental results. Although we obtained favorable result using the optical modeling coefficient, we have not experimental verification about the optimal choice for the coefficient, which will be our next study subject.

Φ : The photon density profile [W/cm²]

q : The light source function [W/cm³]

R : The Robin function, which is the photon density profile with respect to the Dirac delta source [W/cm²]

μ _a : The absorption coefficient [cm^-1]

μ _s : The scattering coefficient [cm^-1]

g : The anisotropy factor

μ _s' : The reduced scattering coefficient [cm^-1] [μ _s' = (1-g) μ s]

κ : The diffusion coefficient [cm] [κ = (3(μ _a μ _s'))-1]

n : The refractive index

a : The reflection coefficient on the surface

c : The speed of light in a vacuum [cm/sec] (c = 2.99×10¹⁰ cm/sec)

ω : The angular modulation frequency of the source intensity [sec^-1]

Ω : The region of interest (skin structure)

∂ Ω : The boundary of Ω (∂ Ω = ∂ ^top Ω ∂ ^left Ω ∂ right Ω + ∂ ^bottom Ω )

∂^top Ω : The top boundary of Ω

∂ ^bottom Ω : The bottom boundary of Ω

∂ ^left Ω : The left boundary of Ω

∂ ^right Ω : The right boundary of Ω

N_b : The number of finite element basis functions