Airy beams, optical versions of the original Airy wavepackets in the context of quantum mechanics [1], are one of several non-diffracting beam solutions whose intensity profiles remain invariant as they propagate through an optical medium. Compared with other types of diffraction-free solutions such as Bessel [2] and Mathieu [3] beams, Airy beams have several unique properties: they are the only non-diffracting solution in the most simple (1+ 1)D configuration and are accelerated during the propagation [4,5]. This acceleration or, to put it more correctly, self-bending is a phenomenal one caused by initial field configurations lacking spatial symmetry. Not only the diffraction-free but also the self-bending features have their origin in the multiple interference between various field components comprising the Airy beam, which maintains its profile during propagation, only changing the peak positions. These attractive characteristics have already been exploited in various applications such as optical trapping/particle manipulation [6,7], plasma waveguiding [8], implementation of Airy plasmons [9], optical bullets [10], dual Airy beams [11], slow non-dispersing wavepackets [12], and the generation of Bessel-like beams [13].

In this paper, we propose waveguide Airy (WAiry) beams: Airy beams propagating through inhomogeneous media with the help of waveguide modes. They not only retain the diffraction-free and self-bending properties of the Airy beam but also inherit the unique features of the waveguide mode such as polarization dependency and slow-light characteristics. Here, we will focus on the WAiry beam associated with the so-called backward waveguide mode [14] and show that the backward feature can alter the trajectories of the WAiry beams significantly, which makes them applicable to the implementation of polarization or power beam splitters.

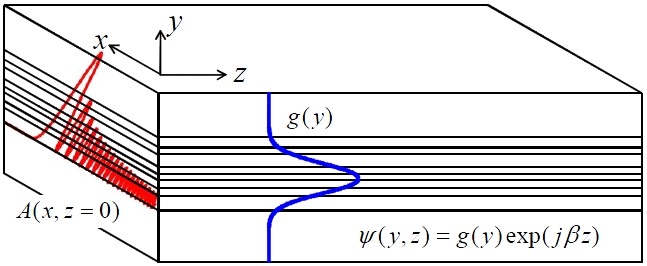
Let us consider a layered or stacked planar waveguide shown in Fig. 1. We have

where φ denotes either E_x (TE-polarized case) or H_x (TM case) field. k₀ is 2π /λ where λ is the wavelength of light

in vacuum, ε and μ are the relative permittivity and permeability of the material. We can easily show that

where ψ (y, z) and g(y) denote a waveguide mode and its transverse profile, respectively, satisfies Eq. (1). A(x, z) is the conventional (1 1)D Airy beam profile given by

where x₀ is an arbitrary scaling factor and α = α ' jα " , α' and α " being related to the initial field profile

where we can find that α' is the exponential apodization parameter for the finite energy carried by the beam and α" is the phase modulation factor along the scaled transverse direction [15].

The above results imply that an Airy beam can propagate in any layered planar waveguides by forming a hybrid beam with waveguide modes. These Airy-like diffraction-free beams, hereafter called waveguide Airy beams or WAiry beams, inherit the characteristics of both the waveguide mode and the Airy beam. We note that WAiry beams are non-diffracting along all spatial directions: diffraction along the y direction is prohibited by the waveguide structure. Along the two other directions diffraction is prevented by the Airy beam profile.

The trajectory of the WAiry beam can be derived by setting the real argument of the Airy function in Eq. (3) to be zero:

where α_x denotes the acceleration along the transverse (+x) direction and θ_z is the initial launch angle [see Fig. 2(a)]. As was clearly discussed in [15], Eq. (5) is equivalent to that describing the constant acceleration motion of particles. When we consider a WAiry beam associated with the backward waveguide mode (in the sense that the overall power flow direction is opposite to that of the phase velocity [14]), β becomes negative for forward power coupling. This negative β flips the initial launch angle θ _z with respect to z since it retains the sign of β . This flipping, although the acceleration direction does not change at all, enables us to separate WAiry beams associated with forward and backward modes.

We would like to propose two such cases in which the relevant two modes are forward and backward ones. In all cases, slab waveguides composed of ε -negative (with ε _E < 0 and μ _E > 0) and μ-negative (with ε _M > 0 and μ _M <0) metamaterials are adopted. For the first case ε -negative and μ-negative metamaterials are dual singly negative ones (i.e., ε _E / μ _E =ε _M / μ_M) As was shown in [16], TE and TM modes in slab waveguides made of dual singly negative metamaterials are degenerate, i.e., |βTE|= |βTM|, but one of them is a backward mode, resulting in βTE = -βTM. Therefore, when the polarization state of light changes, the forward waveguide mode also changes into a backward mode (or vice versa). This implies that the WAiry beams associated with TE and TM waveguide modes can be separated due to the difference in their initial launch angles. Figure 2 shows the splitting of TE and TM WAiry beams in slab waveguides made of dual singly negative metamaterials. We assumed ε_E = -1, μ_E = 1, ε_M = 2, μ_M = -2, a = 0.05 2j, and x0 =1.5λ, and a μ -negative / ε -negative / μ-negative slab structure was considered. The results were obtained using a commercial software (COMSOL) based on the finite element method with the effective index method to reduce the 3D structure into a 2D one. Most optical power flows through the core layer made of an ε -negative medium. The time-averaged Poynting vector <S>, which is inversely proportional to μ_E and ε E for TE- and TM-polarized light, respectively, becomes forward (TE: β // <S> ) or backward (TM: β // -<S>), depending on the polarization state of light. Therefore, we have θ_z^(TE) >0 and θ_z^(TM)<0, resulting in the separation of TE and TM WAiry beams (i.e., polarization beam splitting).

For the second case the waveguide supports dual modes. Dual modes have the same parity and the same number of zero-crossings, but their directions of overall power flow

[FIG. 3.] Power beam splitting of TM WAiry beams associated with backward and forward dual modes. We also assumed the operation wavelength of 1550 nm and a μ-negative / ε-negative/μ-negative slab waveguide with the core thickness of 89.5 nm. εE = -2, μE = 3.5, εM = 3, μM = -1, α= 0.03 2j, and x0 =1.5λwere used. Inset: actual profiles of dual modes.

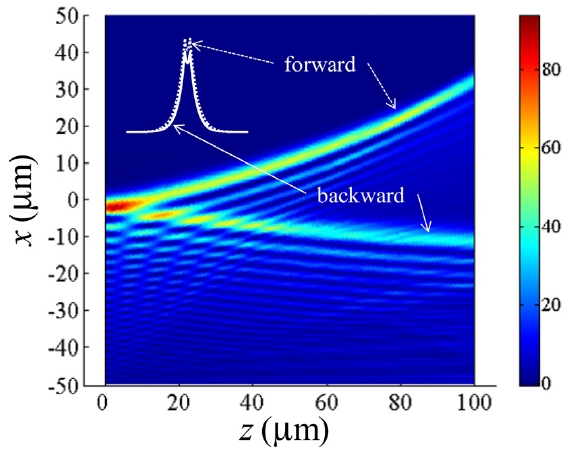
are opposite to each other [14], meaning that dual modes include forward and backward modes. Therefore, the corresponding WAiry beam associated with each of them can also be separated. This characteristic, i.e., power beam splitting, is shown in Fig. 3 where we assumed TM-polarized light waves incident to a μ -negative/ε-negative/μ -negative slab with ε _E = -2, μ_E = 3.5, ε _M = 3, and μ_M = -1. The fact that dual modes have the same parity as well as the same number of zero-crossings, as can be found in the mode profiles shown in the inset of Fig. 3, entails that the coupling efficiencies to two respective WAiry beams associated with dual modes can be made nearly the same, which is very advantageous in the actual implementation of power beam splitters.