The optical properties of composite nanostructures including metal are strongly affected by surface plasmon polaritons’ (SPPs) collective oscillations of conduction electrons with respect to the positive ion background [1-5]. SPPs are the propagating excitations of charge-density waves, and their associated intense electromagnetic fields are generated in the vicinity of the surface of a conductor. They are bound to and propagate along the metal/dielectric interface. Recently, great attention has been paid to the study of the strong coupling between individual emitters and SPPs in metallic nanowires [6-9]. The emission properties of nanoscale optical emitters can be significantly modified by the proximity of a nanowire that supports surface plasmons because an SPP is generally very intense and highly localized [5,7,10]. This subwavelength localization is accompanied by a dramatic condensation of optical fields. A substantial increase in the coupling strength g^∝1/√V_eff can be achieved near the surface of metal nanostructures, since the effective mode volume V_eff of the SPPs can be considerably reduced. For an optical emitter placed within the evanescent SPP mode tail, the spontaneous emission probability of the excited energy of an emitter into the surface plasmons is tremendously enhanced [11-14]. Thus, the controllable strong near-field coupling between emitters and SPPs in metal nanostructures has stimulated a number of studies on nano-plasmonics [15-18].

Near-field coupling of excited colloidal nanocrystals (NCs) to SPPs in a metallic nanowire (NW) is a challenging problem since nanocrystals are randomly dispersed relative to the metallic nanowire [17]. In this paper, we investigate the spontaneous emission (SE) of the excited energy of one NC in NC aggregation to the SPPs in a nearby metallic nanowire for some specified configurations and for specific transition dipolar orientation of NCs. The radius of the NW is to be so small that it is sufficient to consider only the fundamental TE SPP mode in our calculations. In this work, we analyze the cooperative effect in the spontaneous decay of an excited NC in an NC aggregate into a SPP mode with and without the dipole-dipole interaction between NCs [8]. The spontaneous emission rate into surface plasmons can be suppressed or enhanced for specially arranged NCs, depending on their relative positions and transition dipolar orientations due to their quantum interference between the interactions. This variable emission rate can be characterized by cooperativeness, which for thin wires and closely spaced NCs is predicted to be large. In the next section, a theoretical modeling is employed to calculate the transition amplitude of the spontaneous emission under the perturbative expansion scheme. Results of the numerical evaluation for the transition probability (TP) of the spontaneous emission are presented in Sec. III followed by a discussion on its characteristics. A brief conclusion is given in Sec. IV.

The system of interest in this paper is schematically shown in Fig. 1. NCs are supposed to be aggregated around the silver nanowire along the axis, where only one of the NCs is excited. First, we briefly review the properties of SPPs propagating along the surface of metallic NW [19,20], which have been observed experimentally [21-24]. We are especially interested in azimuthally independent SPPs, which are supported under the condition that the radius of the wire is small enough such that only the fundamental TM surface plasmon polariton mode exists while all other higher order modes are cut off [7]. In this case the electric and magnetic fields of the fundamental TM surface plasmon polariton mode are given by [19]

where q stands for inside or outside of the metallic NW with

Here J_n and H_n⁽¹⁾ are Bessel and Hankel function, respectively. The dielectric function ε _q(ω) is taken from the Drude- Lorentz model, i.e., ？_in(ω) = ？_∞[1-ω_p²/ ω (ω+i γ)], where γ is the relaxation rate due to ohmic loss. Since the system does not have azimuthal dependence, the wave number of the SPP has only z dependence. From now on we drop the subscript z for the wave number k_z. The dispersion relation (k, ω_k) of the SPP mode is obtained by applying the boundary condition of the TM mode fields on the surface of the metallic NW [8, 11, 19, 20]

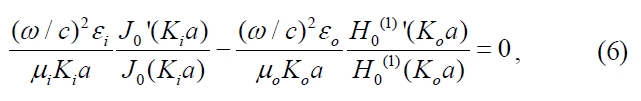
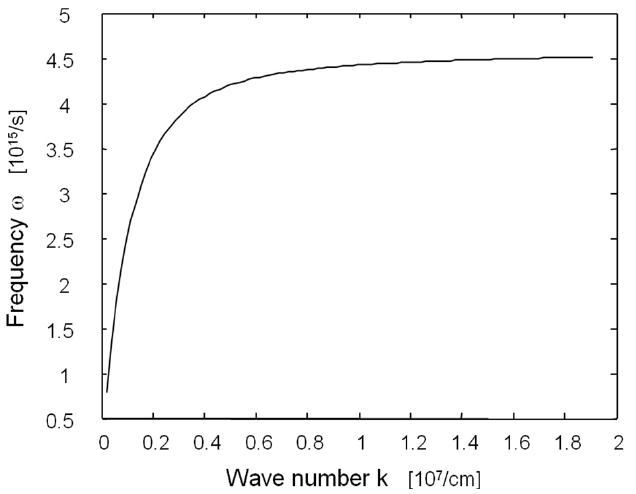
where a is the radius of the NW. The dispersion relation for the fundamental mode of SPP on metallic NW is shown in Fig. 2. The mode-expansion coefficients a_q(k) in Eqs. (1) and (2) are determined by matching the boundary condition of the fields on the metal nanowire/dielectric interface and also by normalizing the electromagnetic fields to their vacuum fluctuation energies [1,8,11]. After performing these operations, the resulting electric field outside the metal becomes

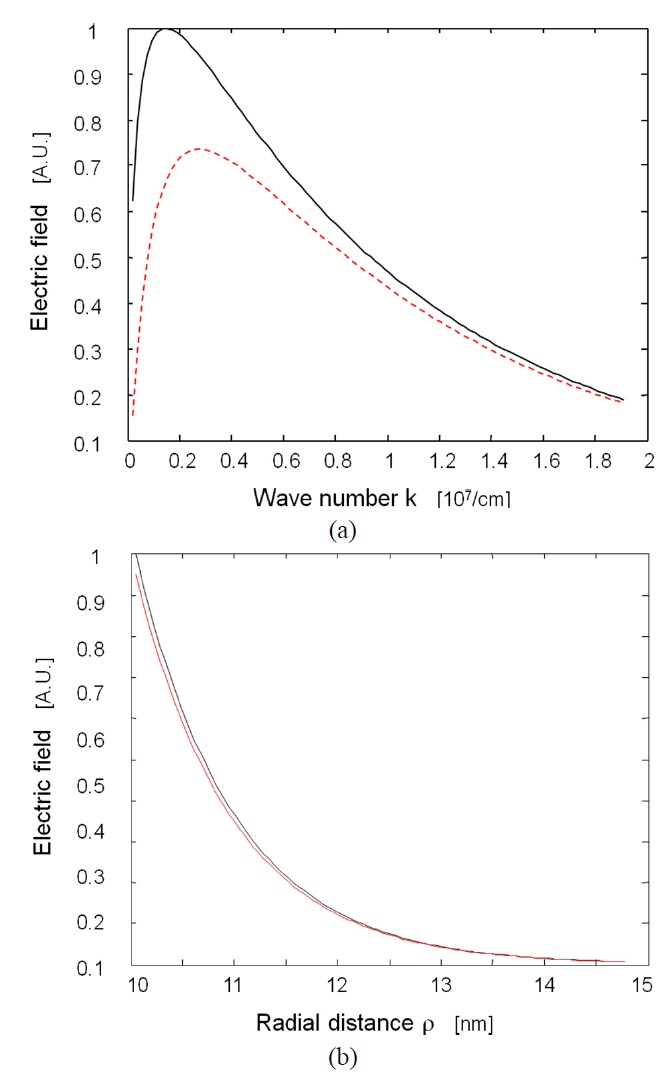
where b(k) is again the mode expansion coefficient but normalized by electric permittivity of the vacuum and nanowire length L, which is averaged over the azimuthal angle for the wire. The radial component of the field is (almost) real and the axial component of the field is imaginary, so that they are out of phase by π /2. The absolute value of the

electric field outside the nanowire as a function of wave number is shown in Fig. 3(a); solid and dashed lines are for the radial and axial components of the field, respectively. Fig. 3(b) is the electric field as a function of radial distance from the wire center. Dramatic concentration of optical fields is well manifested.

The Hamiltonian of this composite system is written by H = H₀ H_int, where H₀ is the unperturbed part and the interaction Hint is given by

where

is the transition dipole moment of the jth NC and

is the electric field at the location of the jth NC due to the surface plasmon polaritons in the nanowire. r_mj and

are the distance and the directional unit vector between mth and jth NCs, respectively. The first term represents the interaction between NCs and NW plasmons, while the second term describes the dipole-dipole interaction (DDI) between NCs. The transition energy of an NC is assumed to be detuned from the surface plasmon polarion mode energy of the metallic nanowire.

The transition amplitude of the SE is calculated from perturbation theory. Within the dipole approximation, the first order transition amplitude of the spontaneous emission from an excited j th NC at (ρ_j, z_j) with transition energy ω _j to a fundamental SPP of mode with wave number k in metallic NW is obtained as

where

and Δ _kj = ω _k？ω_j with

being the electric field of the surface plasmon mode of wave number k at the location of the jth NC. Δ_kj describes the detuning between jth NC’s transition energy and SPP mode energy with wave number k. If all NCs are identical with ωm = ωj and the direct DDI between NCs is ignorable, the third order perturbative transition amplitude of the SE is calculated as

The even-order perturbation terms are null, since the coupling is linear to the dipole moment. Since the NC’s transition energy is detuned from the SPPs in the metallic nanowire and sin(Δ _kk' t/2)/Δ _kk' is a very strongly peaked function of Δ_kk', the last term dominates. Thus Eq. (10) can be approximated by

When all NCs are not identical, the third order perturbative transition amplitude of the SE is similarly calculated, but in this case the detuning parameter Δ_mj between NCs is, of course, explicitly included in the expression

On the other hand, if the direct DDI between NCs cannot be ignored, the second order transition amplitude of the SE term survives. From the calculation carried out for the case when all NCs are identical with only the nearest neighbor interaction, the transition amplitude of the SE is

where J_mj is the dipole-dipole interaction energy between mth and jth NCs in Eq. (8). Similarly, when all NCs are not identical, the second order transition amplitude of the SE is calculated as

The first order TP,

for the SE of an excited NC to a SPP of mode k does not exhibit any collective effect, since it only involves single NC coupling to SPP mode regardless of the existence of other NCs. In order to see the collective effect, the higher order perturbative terms must be examined. We first consider the case without DDI. When we evaluate the total TP composed of

and

the TP would have the cross product contributions between the first and third order transition amplitudes of the SEs. However, neither do they show any substantial collective effect on the same footing as the first order contribution alone. Then, the most important contribution with respect to the cooperative effect comes from the square of

From Eq. (10), the third order TP for the SE of an NC to an SPP of mode

is obtained by

where

and

Here, f (k, k', k", t) is the absolute square of the temporal part in Eq. (10) and it is a function of Δk0, Δ _k'0, Δ _k"0, Δ _kk', and Δ _kk", so that it represents the consequence of detuning effect. As seen from Eq. (15), characteristic collective behavior of this composed system in the third order TP is actually described by the phase factor exp(iΦ _{n, m, k', k"}).

The cooperativeness in the third order TP is manifested by the phase Φ_{n, m, k', k"}, which describes the correlation among the whole NC aggregate. Since the mode of SPPs does not depend on the azimuthal angle, the phase Φ _{n, m, k', k"} of Eq. (16) depends only on the radial and axial locations of NCs. Thus, the cooperativeness is determined by the radial and axial arrangement of NCs, i.e., the locations of NCs ( ρ_j, z_j) and by the dipolar orientation. In order to analyze the collective effect, we consider the dependence of the phase factor on the radial and axial arrangement as well as on the dipolar orientation of NCs. First, the phase difference caused by the axial distribution of NCs in the form of k(z_n？  z_m) in Eq. (16) is always non-negligible since kΔz ~ π even for Δz ~ O(1nm). Thus the axial distribution of NCs along the wire can be an important factor to induce the collective effect in the SE. Next, for the analysis of the phase caused by the radial arrangement and the dipolar orientation, which is represented by the term of θ_j,k in Eq. (16), we consider, for simplicity, the case when the transition dipole vector is in the plane of (ρ, z),. In this case, the absolute magnitude of the NC-SPP coupling strength ?g_j,k? and its phase θj,k are expressed as

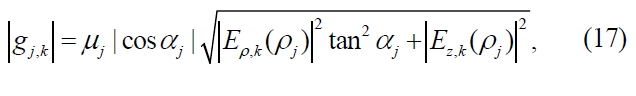
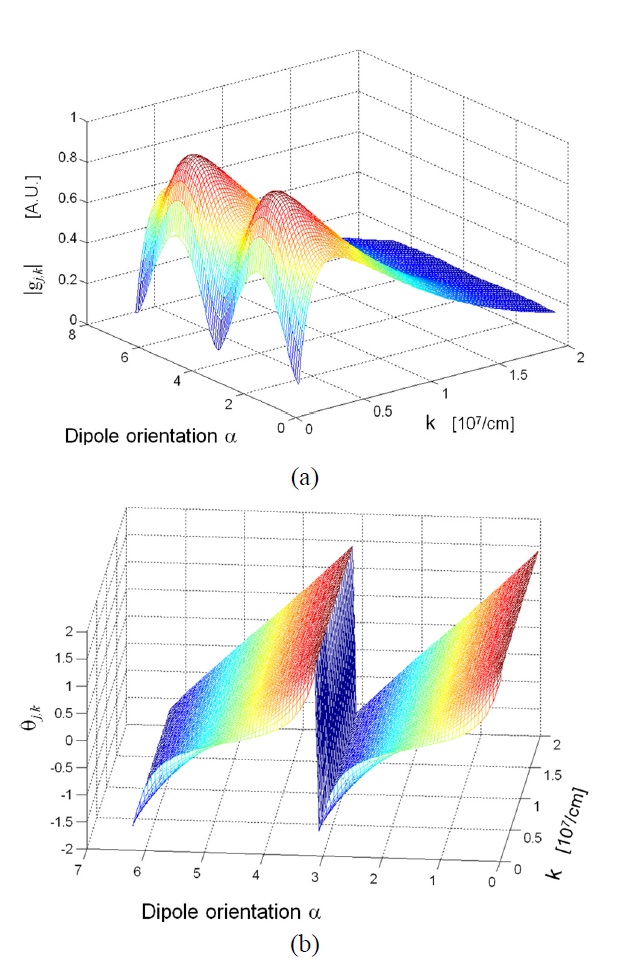
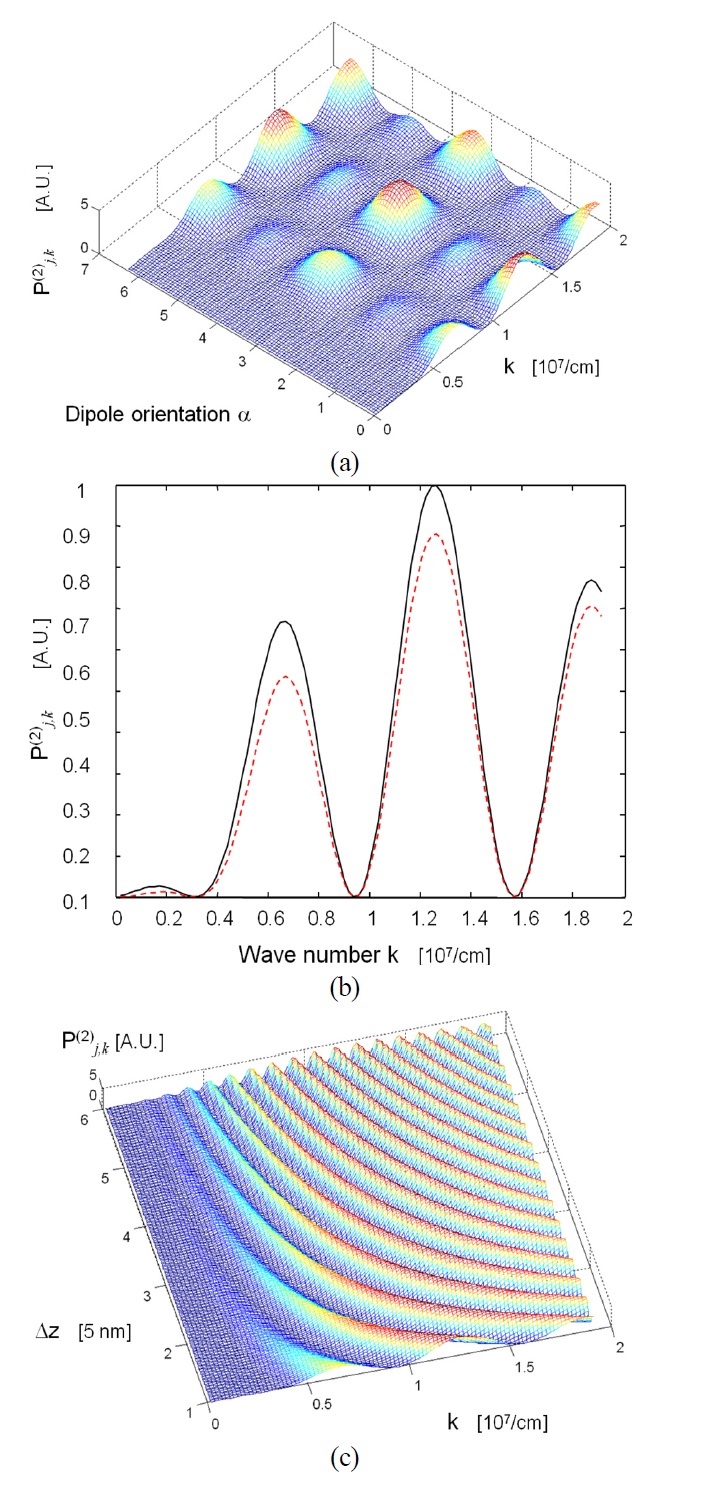
and

respectively, where α_j is the orientation of the transition dipole measured from the wire axis. |g_jk| and θ_jk as functions of k and α_j are shown in Fig. 4(a) and 4(b), respectively.

Now we consider the collective effect of the SE in the third order TP. As was pointed out in the previous section, the terms with (sin Δ _kk' t/2)/Δ _kk' and (sin Δ ;_kk" t/2)/Δ _kk" in f(k,k',k",t) of Eq. (15) dominate, since NC’s transition energy is detuned from the SPPs in the metallic NW. The amplitude of the function (sin Δ_kk' t/2)/Δ_kk', which is very highly peaked at Δ _kk' = 0, increases as t and decreases to zero when Δ_kk' = 2π/t. When time t ~ z_n (dk/dω) is small enough as ~ fs or less, non-resonant coupling between SPP modes is allowed in the third order process. In this situation, the phase Φof Eq. (16) is not negligible. That is, the phase difference with the form of z_n(k?k') in Eq. (16) is order of π for the time being ~ fs or less in which Δ z is assumed to be ±10nm. On the other hand, in the longtime limit, Δ_kk' ？ Δ_kk" ？0 and for the most part only the resonant coupling between SPP modes is allowed in the third order process. In this circumstance, there are many cancellations among the phases in Eq. (16), so that no appreciable collective effect is expected. In this resonant coupling approximation, the third order transition probability of the SE can be approximated as

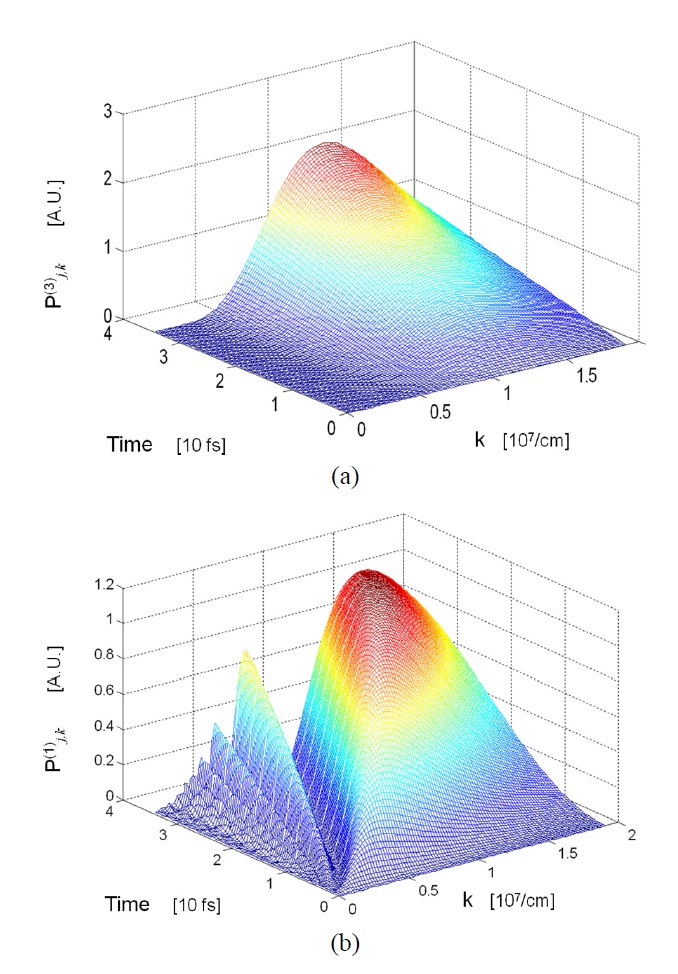
which is plotted as a function of k in Fig. 5(a). Since the transition energy of an NC is assumed to be detuned from the SPP mode energy of the NW and to be above the mode energy, the TP of the SE will increase as the size of NCs increases. That is, when the size of NCs increases, the transition energy of NCs decreases and then Δ_kj in Eq. (19) will decrease. In the case of non-identical NCs, it can be further approximated as P_k⁽³⁾(t)(1 Δ _jm / Δ _kj)^-2, which shows reduced transition probability of the SE for increased disparity in the size of NCs. As a reference, the first order TP of the SE to the k mode of SPP P_k⁽¹⁾(t) is given by

and is shown in Fig. 5(b), for comparison. No noticeable

change for TP is observed with regard to including multiple interactions between NC and SPP.

Now we analyze the cooperative effect due to direct DDI. When all NCs are identical, the second order TP of the SE to the k mode of SPP, P_k⁽²⁾(t) is obtained as

where

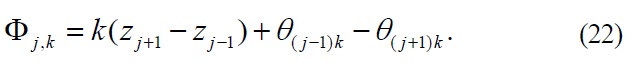
The cooperativeness of NCs is involved in the phase Φas the case without DDI. As described above, the phase difference caused by the axial distance between NCs, is order of π for Δz ~ 10 nm. On the other hand, the phase difference, Δθ = θ _m,k？θ_n,k is induced by the radial distribution and the dipolar orientation of NCs, as seen from Eq. (18). Since the radial component of the electric field is (almost) real and the axial component of the electric field is imaginary, there is no interference effect coming from the NC-SSP coupling difference as seen from Eq. (18), if the transition dipole is arranged only along the wire or only perpendicular to the wire axis. Thus the phase difference Δ θ in Eq. (22) depends strongly on the dipolar orientation. This character is plotted as a function of α and k in Fig. 6(a). The figure shows that, for a given transition dipolar orientation of NCs, the SE of an excited NC into several specified modes of the fundamental SPP in the metallic nanowire is totally inhibited.

When the radial distances of NCs from the wire center are almost the same among the NC aggregates (？g_m,k？？？g_k？) and the orientations of NC’s transition dipoles are parallel to each other with DDI coupling J, the transition probability of the SE is approximated as

In this case, the phase difference Δθ of Eq. (22) almost vanishes and the phase is determined by the difference of axial distance between NCs, which is plotted as a function of Δz and k in Fig. 6(c). The effect of interference on the SE due to the second order TP caused by the direct DDI is explicitly shown in the figure. For a given configuration of NCs, the SE to a certain specified SPP modes is totally

suppressed, as expected. And when all NCs are arranged along the NW, the TP of the SE will decrease as the distance between the NCs and the NW increases as seen from Fig. 3(b).

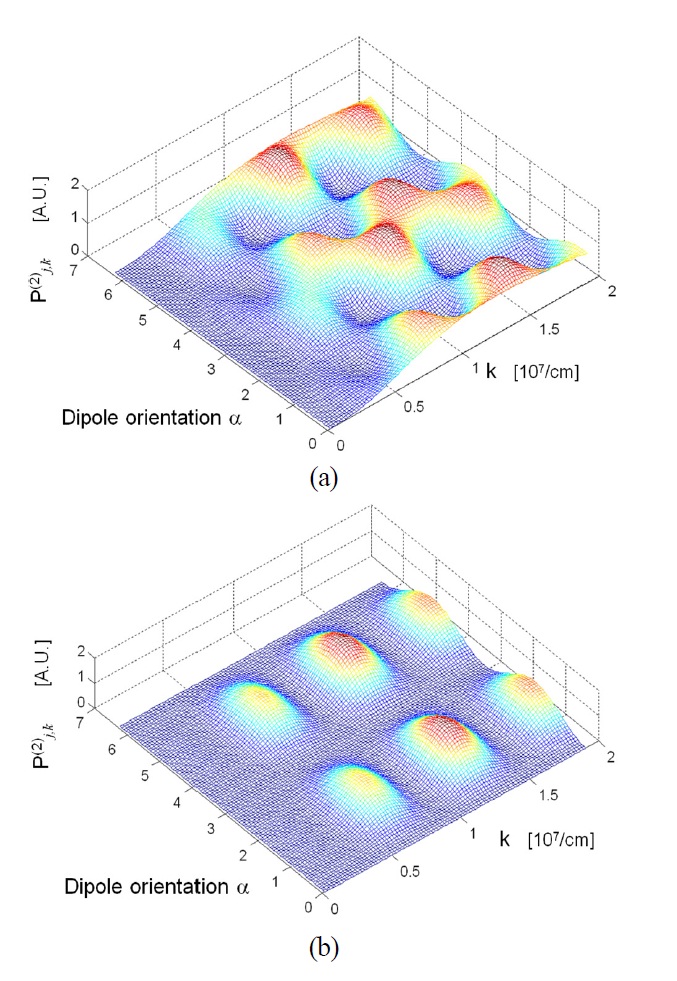
In practice, the phase difference Δθ caused by the radial distribution between NCs is appreciable, however the effect of the radial distribution of NC on the cooperativeness in the second order TP is negligible due to the huge difference of the field |E(ρ_n)|-|E(ρ_m)|, which causes low visibility for the interference pattern of Eq. (21). Since the phase difference Δθ depends strongly on the dipolar orientation, the effect of dipolar orientation on the cooperativeness in the second order TP is considered by dealing with two simple cases. For instance, when there are three NCs with similar radial distances ρ_j ？ρ and if

the second order TP as a function of α and k is obtained as shown in Fig. 7(a). On the other hand, if the first and the third dipoles point along the radial direction, i.e.,

the transition probability of the SE as a function of α and k behaves like Fig. 7(b). Here, we have analyzed the TP of the SE when only one NC is

excited. Meanwhile, if two or more NCs are excited, then the TP of the SE will strongly depend on the initially prepared state. For the case without the interaction between excitons, if the NCs are excited in the form of a superradiative (subradiative) state, the emission rate will be enhanced (suppressed) [25].

In summary, we have analyzed the characteristics of the cooperative feature of the spontaneous emission of one excited NC among NC aggregate into a mode of SPP in a metallic nanowire. In order to see the collective effect of the SE, higher order perturbation expansions of the transition probability of the SE have been derived. In particular, the influence of the dipolar orientation and the axial and radial arrangement of NCs has been considered. The first-order transition probability of the SE does not show collective behavior. Also the collective effect disappears in the thirdorder process of the spontaneous emission when direct DDI is not involved under the resonant coupling approximation between SPPs. However, the second-order transition probability of the SE yields a cooperative effect of the SE. In particular, the spontaneous emission of the excited NC energy is suppressed or enhanced depending on the relative orientation of the dipoles and the arrangement of NCs.