Organic solar cells (OSCs) have been intensively investi-gated as one of the promising green energy sources due to the feasibility of producing thin, light-weight, and flexible solar cells [1]. However, the power conversion efficiency should be further improved for practical use of the OSC. Optical interference effects play an important role in the efficiency of multilayer OSCs, where the thickness of each thin-film layer should be carefully designed to maximize the optical absorption in the active region.

The optical interference effect of the multilayer solar cells has been modeled based on the finite element method (FEM) [2, 3], the rigorous coupled-wave analysis (RCWA) [4, 5], and the transfer matrix method (TMM) [6-8]. Among them, the TMM has been widely used for thin-film OSCs due to its relatively ease of simulation code implementation but high accuracy in calculation results. The TMM-based optical model for the OSC provides the spatial distribution of the time-average optical power dissipation Q (z)usually for normal incidence of sunlight [6-8]. Here, Q(z) is related with the amount of photon energy absorbed by the material per unit time and per unit volume and z is a position within the multilayer OSC.

Recently, the angular response of thin-film OSCs with respect to the incidence angle of sunlight has been intensi-vely investigated due to the fact that most OSCs, having the advantage of low-cost production and flexible appli-cation,are expected to be used without a sunlight tracking system. The TMM-based optical model for normal incidence has been adopted for oblique incidence to analyze the angular response of thin-film OSCs [9-11]. However, the previous TMM-based optical models for oblique incidence of sunlight are still insufficient.

It was mathematically proved that Q(z) can be expressed as Q(z)= (1/2)cε₀nα|E(z)|² for normal incidence of sunlight[6]. Here, c is the speed of light in free space, ε₀ is the permittivity in free space, n is the real part of the complex refractive index, α is the absorption coefficient, and E(z) is the electric field amplitude at the position z. In the case of oblique incidence, Q(z) was also assumed to be pro-portional to |E(z)|² for both s- and p-polarized sunlight[10, 11]. However, we have not yet found any text to provide a clear derivation for the relation between Q(z) and |E(z)|² at oblique incidence, especially for p-polarized light. In addition, the effect of the incidence angle and light polarization on the distribution of Q(z) has not yet been investigated quantitatively.

In this paper, we present comprehensive optical modeling and calculation results of thin-film OSCs at oblique incidence of sunlight. By applying the TMM at oblique incidence, we derive a simple expression for Q(z) for both s- and p-polarized light. We calculate the spatial distribution of the electric field intensity, the time-average Poynting vector(optical power density), and the optical power dissipation with respect to the incidence angle. We investigate how the optical interference effect of thin-film OSCs is affected by the incidence angle and light polarization.

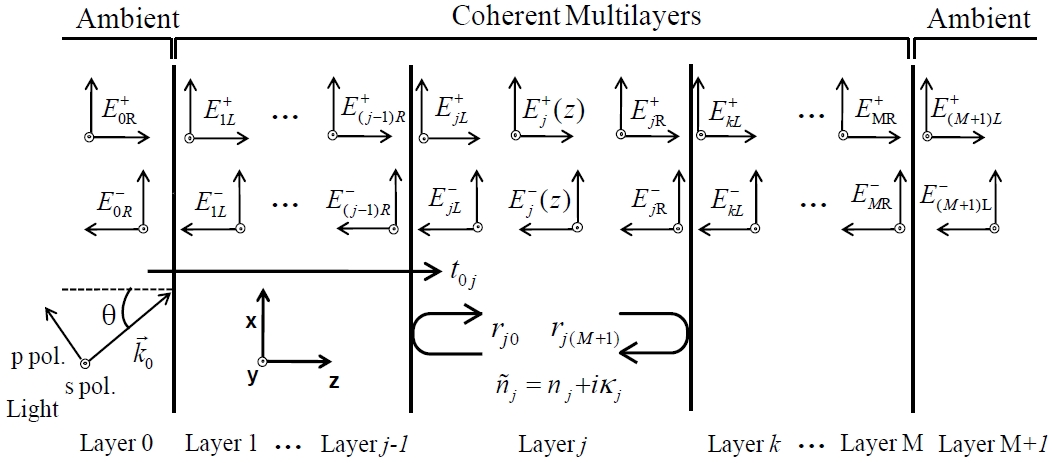
Fig. 1 shows a stack of M layers, where a plane wave with an incident angle θ and a wavelength λ is incident from the semi-infinite transparent ambient on the left (j=0). The multilayer stack is assumed to be isotropic and homo-geneous with plane and parallel interfaces. The orientation of the electromagnetic field oscillations is composed of s-polarization and p-polarization that are perpendicular to or parallel to the incident plane, respectively. Each thin-film layer j (j=1, 2, …, M) has a thickness of d_j and a complex refractive index of

where n_j and Kj are the refractive index and extinction coefficient, respectively.

In Fig. 1, the wave vector in the transparent ambient of the 0-th layer is given by

where n₀ is the refractive index of the 0-th layer and k₀=2π/λ . In the j-th layer, the wave vector is written as

where the relation k_x,j=k_x,0 is ascribed to the boundary condition that the transverse wave vector should be continuous at the interface. The terms

and

correspond to the effective refractive index and the extinction coefficient for the z direction. From the dispersion relation

we have

Consequently, we obtain

In Fig. 1, we assign a positive (negative) direction to the light propagating from left (right) to right (left), designating the + (-) superscripts. The electric field amplitudes on the interface between the adjacent layer j and k=j+1 are described by an interface matrix I^jk:

where

and

are the forward-propagating electric field amplitudes at the right boundary of the layer j and the left boundary of the layer k, respectively. The terms r_jk and t_jk are the complex Fresnel reflection and transmission coefficients on the interface of the adjacent layer. For s-polarized light, they are defined as [12]

and for p-polarized light as

The propagation of the electric field amplitude between the left and right boundaries of the j-th layer is described by a layer matrix L^j:

where we assume the time dependence of e^iwt.

In Fig. 1, the electric field amplitude passing through all the M multilayers from the ambient on the left (layer 0) to the right (layer M+1) can be written as

where the amplitude scattering matrix S^0/(M+1) is defined as

If there is no incidence of light from the ambient on the right (layer M+1) to the left (layer 0),

and the front-reflection and front-transmission coefficients from the layer 0 to M+1 can be obtained by

In the same manner, we can define the complex reflection and transmission coefficients for the j-th layer in terms of the matrix elements

As shown in Fig. 1, t0j is the internal transmission coefficient from the ambient on the left (layer 0) to layer j. The terms r_j0 and r_j(M+1) are the internal reflection coeffi-cients through the partial front multilayers from layer j to layer 0 and through the partial rear multilayers from layer j to layer M+1, respectively.

The y component of the electric field in the j-th layer is expressed as

where

is an internal transfer coefficient, relating the incident plane wave to the internal electric field propagating in the positive (negative) z direction at the interface between the layer j-1 and j [13]. The values of

and

are given by

where t_0j, r_j(M+1), and rj0 are defined in Eqs. (11). The corresponding magnetic fields are

The time-average Poynting vector in the z direction is expressed as

where we can define

Finally, the optical power dissipation in the z direction is given by

where

and α j,θ=2_qjk₀ in Eq. (18) are the real part of the complex refractive index and the absorption coefficient at the incident angle θ , respectively. We can obtain Eq. (19) by substituting Eq. (12) into Eq. (18). Similar to normal incidence, the optical power dissipation at the incident angle θ is also proportional to the electric field intensity for s-polarized light. It is noticeable that the values of p_j and α _j,θ are modified for oblique incidence compared with the case of normal incidence.

The x and z component of the magnetic field in the j-th layer can be written as

The corresponding magnetic field is given by

The time-average Poynting vector in the z direction is given by

Finally, the optical power dissipation in the z direction is written as

Rearrangement of Eq. (24) together with Eq. (3) leads to

By substituting the expressions for E_x,j and E_z,j in Eqs.(20) and (21) into Eq. (25), we obtain

It is remarkable that the optical power dissipation for p-polarized light at oblique incidence is also proportional to the electric field intensity, which is composed of the x and z components of the electric field amplitude for p-polarized light. Thus, information on the electric field intensity with respect to light polarization and incident angle is sufficient to calculate the optical power dissipation in the OSC.

Because light absorbed in the active region of the OSC can contribute to the electric power generation, we have to maximize the light absorption efficiency at the active region to enhance power conversion efficiency of the OSC. The light absorptance of the layer j (d_j-l≤z≤d_j) can be expressed as [8]

where

is the optical power of sunlight light with s(p) polarization, which is incident from the ambient on the left.

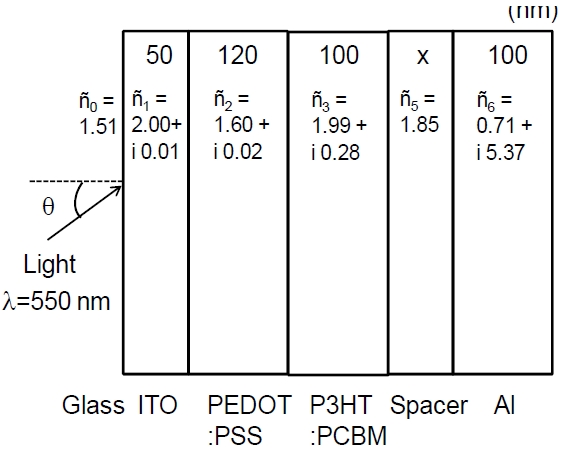
Fig. 2 shows the multilayer structure of the OSC along with its corresponding complex refractive index, which is

taken from Ref. 14. The wavelength of light is assumed to be 550 nm, where the P3HT:PCBM active layer has a peak absorption. We consider the incident angles of 0°, 30°, 45°, and 60° in this calculation. The thickness of the optical spacer layer is varied as x = 50, 100, and 150 nm to adjust the optical interference effect and maximize the electric field intensity distribution within the active region.

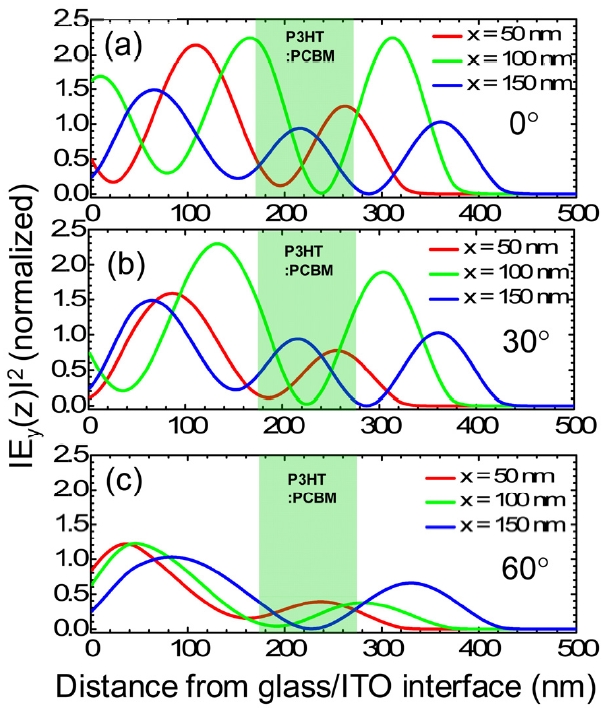
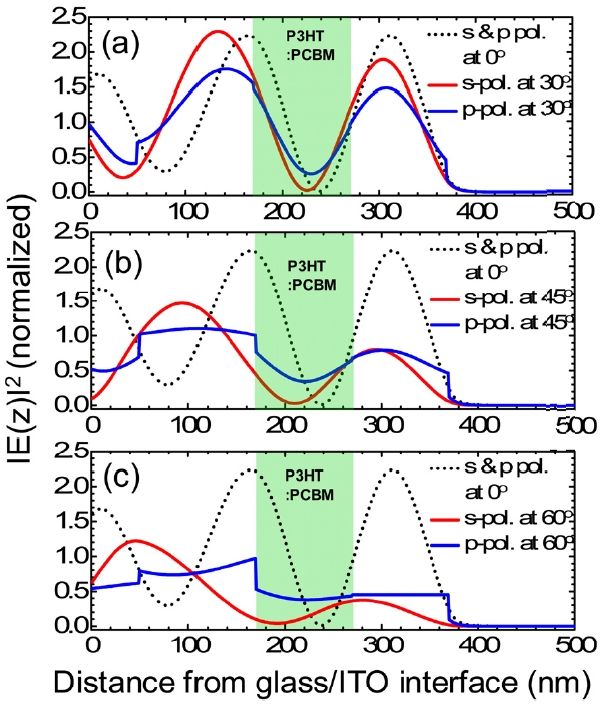
Fig. 3 shows the y component of the normalized electric field intensities at the spacer thickness of 50, 100, and 150 nm. The light green area in the middle of Fig. 3 indicates the P3HT:PCBM active region, where the electric field intensity distribution is important for determining the efficiency of the OSC. The value of the electric field intensity is normalized to s-polarized light incident from the transparent glass on the left ambient when the incident angle is (a) 0°, (b) 30° and (c) 60°. From the ITO toward the Al layers, the oscillating electric field intensities show the general inter-ference pattern [6-8]. For normal incidence (θ = 0°), the spatial distribution of |E_y|² in the P3HT:PCBM active region is the largest at the spacer thickness of 100 nm, where the OSC expects to have the best light absorption efficiency. As the incident angle increases to 30° and further up to 60°, the overall oscillating interference pattern of |E_y|² moves toward the ITO layer. This behavior is ascribed to the fact that the real part of the complex refractive index,

becomes smaller at the larger incident angle.

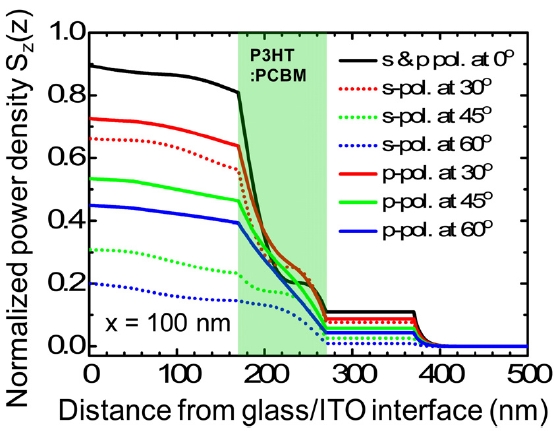
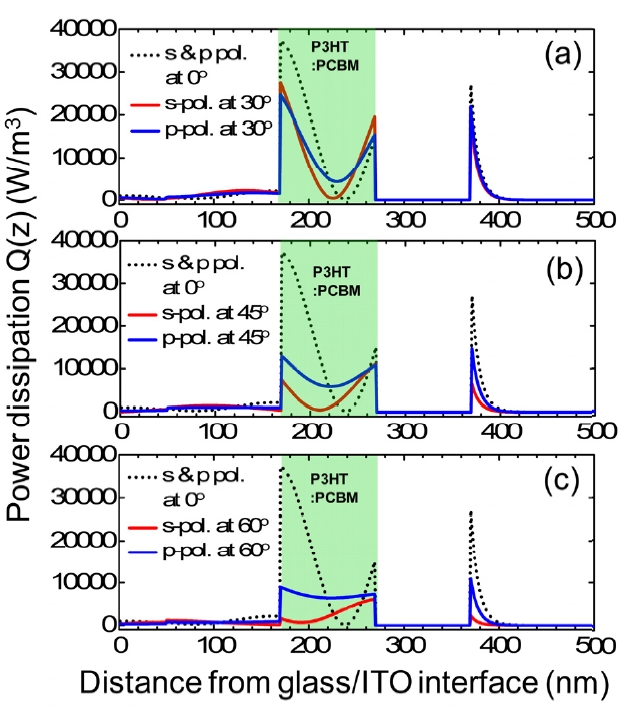
Fig. 4 shows the time-average Poynting vectors S_z(z) for s- and p-polarized light at the incident angles of 0°, 30°, 45°, and 60°. The thickness of the optical spacer layer is fixed as x = 100 nm. The calculated time-average Poynting

vectors are normalized in reference to the incident optical power from the transparent glass. As the incident angle increases, the value of Sz(z) at the glass-ITO interface (z = 0 nm) decreases because the front-reflection coefficient of the OSC multilayer, r_0(M+1) in Eq. (10a), becomes larger at the higher incident angle. The value of Sz(z) with normal incidence (θ = 0°) is identical and degenerate for s- and p-polarized light. However, the value of Sz(z)\with oblique incidence of p-polarized light is larger than that with oblique incidence of s-polarized light. This higher trans-mittance of p-polarized light over s-polarized light at oblique incidence is similar to the transmission behavior at the boundary between two dielectric media, where the Brewster’s angle(100% transmission) is existent for p-polarized light [12].

Fig. 5 shows the comparison of the calculated normalized electric field intensities between s- and p-polarized light at the incident angles of (a) 30°, (b) 45°, and (c) 60°. For reference, the normalized electric field intensity distribution at normal incidence is shown in the black dotted line. The optical spacer layer thickness is x = 100 nm. The electric field intensity for p-polarized light |E^p|² = |E_x|² + |E_z|² is discontinuous at the interfaces because it has the electric field intensity component of |E_x|² normal to the interface. On the other hand, the electric field intensity for s-polarized light |E^s|² = |E_y|² is continuous at the interfaces because it has only a transverse electric field intensity component. Fig. 6 shows the calculated optical power dissipations in the z direction for s- and p-polarized light as a function of

the incident angle. According to the definition of light absorptance in Eq. (27), p-polarized light shows the relati-vely higher light absorptance in the P3HT/PCBM active region than s-polarized light does This is more pronounced as the incidence angle increases from 30° to 60°.

We presented comprehensive optical modeling and calculation results of thin-film OSC at oblique incidence of light. Based on the TMM, the simple expression for the optical power dissipation was derived at oblique incidence for s- and p-polarized light. Depending on light polarization, we calculated the spatial distribution of the electric field intensity, the timeaverage Poynting vector, and the optical power dissipation at various incidence angles. As the incidence angle increases, the optical power dissipation in the active region becomes smaller for both s- and p-polarized light. In the P3HT/PCBM active region, p-polarized light shows relatively higher light absorptance than s-polarized light does. This is more significant as the incidence angle increases up to 60°. We expect that our optical modeling results help to design more efficient OSC with light absorption efficiency improved,considering the optical interference effect of the OSC at oblique incidence.