So far, Brillouin scattering based sensors have been studied as promising technology for a distributed temperature or strain measurement in structural health monitoring [1-10]. Intrinsically, Brillouin scattering is an effect caused by acoustic vibrations in the medium when laser light travels in a medium such as an optical fiber. Since the sound wave is traveling, light is also subjected to a Doppler shift, so its frequency changes. The Brillouin frequency shift ν_B can be calculated from the effective refractive index of the propagating media n, the acoustic velocity V_a, and the wavelength of the incident light λ :

On the other hand, in optical fibers, the acoustic velocity depends on the material density ρ [11]:

where K is the bulk modulus.

Since any temperature variation or deformation experienced by the fiber will also have an impact on its density, the Brillouin frequency will be shifted with the temperature or strain as expressed in Eq. (1) and (2). Also it is known that Brillouin frequency shift (BFS) is linearly proportional to these two quantities [9]:

where ε is strain, t is temperature, t_r is reference temperature, and C_s and C_t are the proportional coefficients of strain and temperature, respectively. (C_s = 4.6, C_t = 9.4 × 10^-5 K).

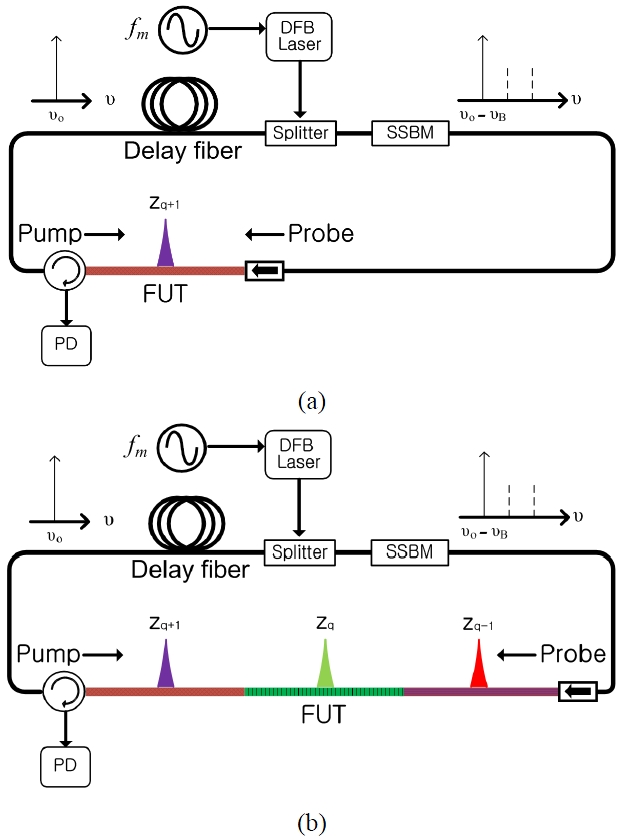
Among many Brillouin scattering based sensors, the most extensively studied techniques are Brillouin optical time domain reflectometry (BOTDR), Brillouin optical time domain analysis (BOTDA), and Brillouin optical correlation domain analysis (BOCDA). BOTDR and BOTDA have an advantage of long measurement range of several tens of km. However, their long measurement time (~ several minutes) and limited spatial resolution (> 50 cm) may prevent some specific applications for health monitoring of structures such as aircraft wings, rockets, and wind turbine blades. Meanwhile, BOCDA has a high spatial resolution (~ cm order) and a high sampling rate (~ kHz) with random access of sensing position. In this system, modulation parameters (amplitude and frequency) of a light source must be chosen such that only a single correlation peak lies within the sensing fiber. Thus, there is a trade-off problem between the spatial resolution and the measurement range [12-14]. Several techniques have been introduced to extend the measurement range while maintaining the spatial resolution such as optical time gating [14] (the measurement range: 250 m, the spatial resolution: 8 cm), double frequency modulation [15] (the measurement range: 34 m, the spatial resolution: 10 cm), and using different kinds of fibers [16]. Particularly, in [16], they demonstrated two times enlargement of strain distribution measurement range by using two different kinds of fibers and a typical electro-optic modulator (EOM) with the measurement range of 8 m and the spatial resolution of 4 cm. In this scheme, it is undesirable for the modulation amplitude Δf to be higher than the Brillouin frequency ν_B, since it suffers the reduction of signal due to counterbalancing of Brillouin gain and loss when Δf is larger than ν_B, where spectrum overlap occurs between the two sidebands from the EOM [17]. Since the spatial resolution is inversely proportional to Δf, there is some limit of spatial resolution in that scheme. Moreover, it requires a proper optical filter to distinguish the probe signal from the backward reflected pump waves at the overlapped frequency.

To solve these problems, we use a single sideband (SSB) modulator instead of an EOM. In this scheme, Δf can be higher than ν_B, capable of achieving high spatial resolution. Additionally, to circumvent a beat noise between the lock-in frequency and the modulation frequency, we used a variation-frequency lock-in detection method [18]. Also we adopted a polarization diversity scheme to avoid the signal fluctuation due to polarization change of probe and pump light.

In the typical BOCDA system, a sinusoidal frequency modulation is applied to the pump and probe waves, producing periodical correlation peaks along the test fiber [3]. The periodic correlation position z_q is given by [19]:

where f_m is the modulation frequency of the light source, c is the light speed in vacuum, n is the refractive index, q is

an integer, l_d and l are the length of delay fiber and test fiber, respectively. By adjusting the length of delay fiber, we can locate only one non-zero correlation peak z_q along the fiber under test (FUT) sandwiched between the circulator and the optical isolator as shown in Fig. 1(a). And the stimulated Brillouin scattering is generated only at this correlation peak. Therefore, we can selectively obtain the information of the stimulated Brillouin gain spectrum (BGS) at the correlation peak position. This correlation peak, i.e., measuring position, is scanned by sweeping the modulation frequency f_m. Therefore, spatial range of measurement is limited to the interval of the correlation peaks d_m:

where V_g is the group velocity of light. Here, the spatial resolution Δz is given by:

where Δν_B is the Brillouin gain bandwidth and Δf is the amplitude of frequency modulation of the light source. From above two equations, the number of sensing points N_R can be calculated as:

Accordingly, to increase the measurement range, modulation frequency f_m must be lowered or modulation amplitude Δf must be increased. When f_m is lowered, the spatial resolution is deteriorated from Eq. (7). Therefore large Δf is required to extend the measurement range while maintaining the spatial resolution. However, it is not easy to increase Δf. Another method for enhancing the measurement range is to utilize multiple correlation peaks. In this technique, different kinds of fibers with different Brillouin frequency are connected to compose of FUT [16]. Furthermore, the length of each fiber is set in order that only one correlation peak is located in each fiber. Thus, strain distribution in each fiber can be selectively obtained by adjusting the sweep region of the microwave frequency ν since each Brillouin gain signal is well separated due to different Brillouin frequency shift among the fibers. Thus, the measurement range can be multiplied. For example, as shown in Fig. 1(b), assume that FUT is composed of three sections of fibers with different Brillouin frequencies which are connected by the correlation peak interval such that only one correlation peak is located on each fiber. By sweeping the microwave frequency wide enough to cover three different Brillouin frequencies, we can obtain overall strain distribution of the FUT. Accordingly, the measurement range can be expanded three times while maintaining the same spatial resolution.

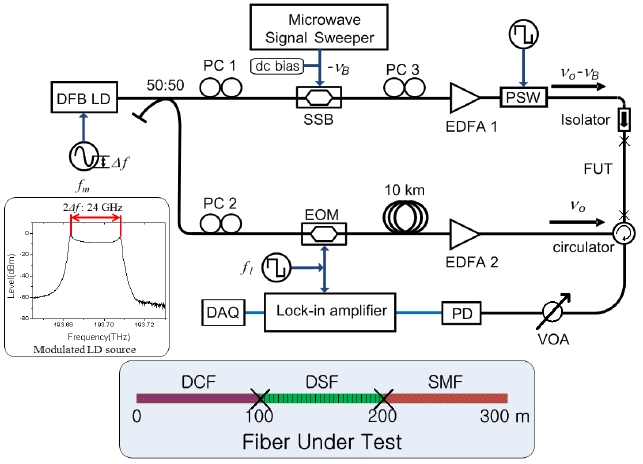
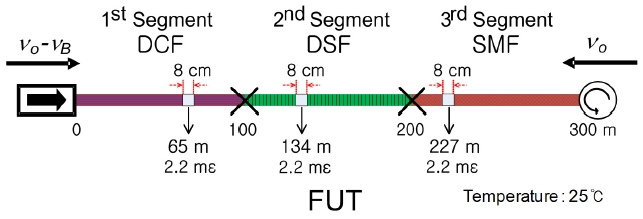
The experimental setup is shown in Fig. 2. A FUT was constructed by splicing 100 m-DCF, 100 m-DSF and 100 m-SMF, which have different Brillouin resonance frequencies.

As a light source, 1548 nm-distributed feedback laser diode (DFB-LD) was used, and a sinusoidal frequency modulation was applied to generate two correlation peaks within FUT. The modulation frequency f_m was set to 1.0112-1.0313 MHz depending on the measurement position (i.e., the correlation peak) in FUT and modulation amplitude Δf was about 12 GHz. From these parameters the spatial resolution and measurement range was estimated to be about 8 cm from Eq. (7) and 100 m from Eq. (6), respectively. The output from the DFB-LD was divided into two beams by a beam splitter. One of the beams was used as the Brillouin pump after passing through 10-km delay fiber to control the order of correlation peaks and a high power erbium doped fiber amplifier (EDFA). The other beam was injected into the SSBM which was driven by a microwave signal generator, so that the first lower sideband, serving as the probe light, was generated and propagating against the pump in the FUT. Before entering the FUT, the pump and probe powers were about 30 dBm and 23 dBm, respectively. Additionally, a polarization switch (PSW) was inserted after the SSBM for suppressing the polarization dependence of the Brillouin signal [3]. Moreover, the pump light was chopped by an intensity modulator for lock-in detection and the lock-in frequency was chosen to get a sharp Brillouin peak and noise suppression. During the position sweep measurement, f_l was varied according to the relation f_l = f_m/4 (f_l is lock-in frequency and f_m is modulation frequency) for minimizing the beat noise [18]. A 125-MHz photo receiver was used as a detector and the BGS was obtained through a lock-in amplifier.

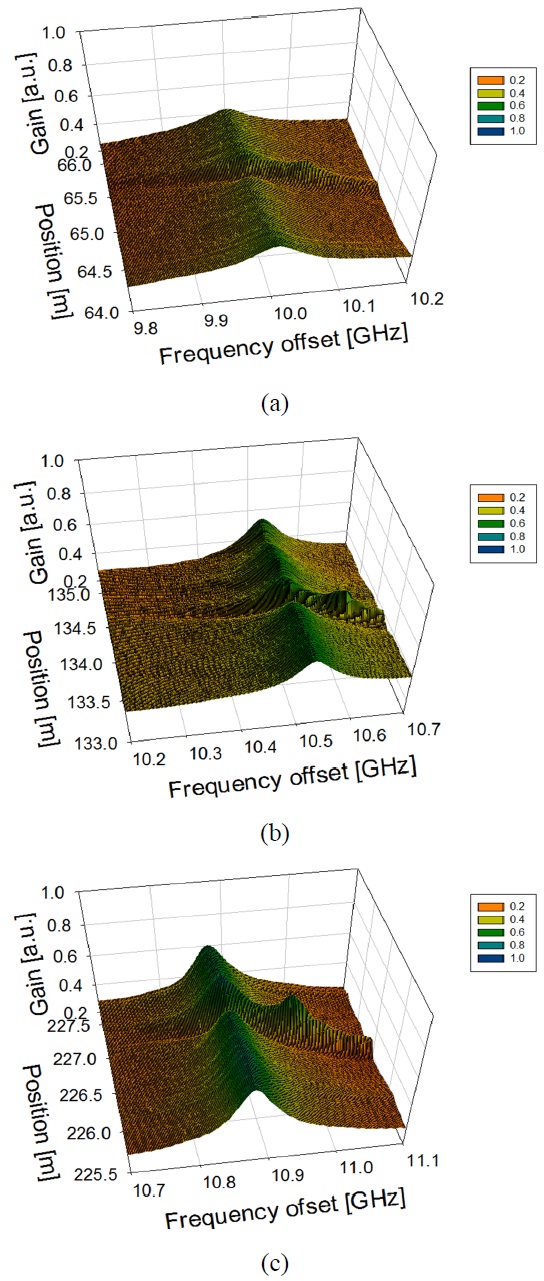
As a proof of concept experiment, we performed measurement of BGS along the FUT, in which the strain of 2.2 mε was applied to three 8-cm sections and a temperature was maintained by an environment control system at 25℃ as shown in Fig 3. There are three correlation positions within the FUT: One is located in the DCF (0-100 m), another one in the DSF (100-200 m) and the third in the SMF (200-300 m). Since the ν_B of each fiber is different, we can selectively measure BGS distribution in each fiber by adjusting the sweep frequency.

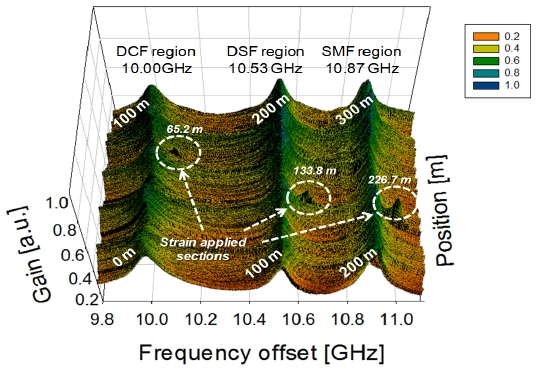
The BGS was measured every 4 cm along the FUT, sweeping Δν from 9.8 to 11.1 GHz. There are three Brillouin gain peaks in the spectrum and each peak comes from a different position (z_q+1, z_q and z_q-1 in Fig. 1(b)) along the FUT. The measured distributed BGS along the FUT is shown in Fig. 4. Clearly different Brillouin frequencies

are observed in each fiber. Note that the ν_B of each fiber was around 10.0 GHz, 10.53 GHz, and 10.87 GHz for DCF, DSF, and SMF, respectively.

Fig. 5 shows an expanded view of the distributed BGS of the circled segments shown in Fig. 4.

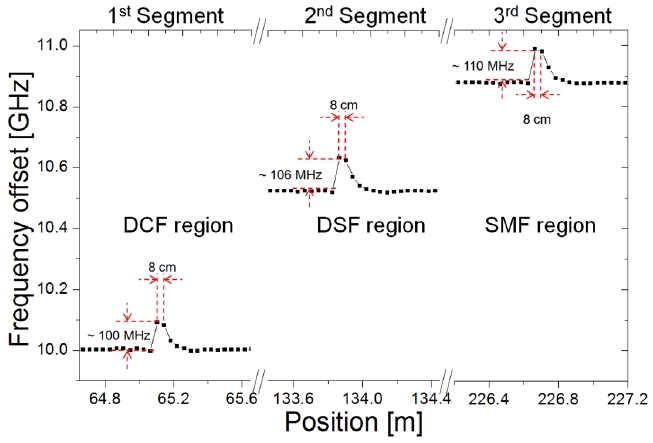
On the other hand, Fig. 6 shows the distribution of the BFS derived from the data of Fig. 5(a)-(c). The spatial resolution was calculated to be about 8.0 cm by Eq. (7). We can observe clear Brillouin frequency shifts (BFS) at the strain applied sections. The change of the BFS was about 100 MHz, 106 MHz, and 110 MHz for DCF, DSF, and SMF region, respectively, which agree well with the applied strain of 0.22%. Also the BFSs have different slopes of BFS which are 0.046 MHz / 1 με , 0.0484 MHz / 1 με and 0.05 MHz / 1 με for DCF, DSF, and SMF, respectively by Eq. (3). The measurement error was about +/- 3.5 MHz, corresponding to the strain accuracy of +/- 0.007% (+/-70 με ).

Thus, we successfully demonstrated strain distributed measurement over 300-m measurement range with 8.0-cm spatial resolution by using the proposed scheme, which has three times larger measurement range than that of the conventional BOCDA system.

In conclusion, we achieved a factor of 3 expansion of measurement range in BOCDA system by using different kinds of fibers while maintaining the spatial resolution. In this technique, multiple correlation peaks within the sensing section can be utilized since any correlation peak point can be arbitrarily selected due to different Brillouin frequency shifts. In the experiment, by adopting the SSBM and variation -frequency lock-in detection technique, we could get a better spatial resolution. We expect that the proposed BOCDA system could be useful in the strain monitoring of civil structures.