Nowadays, as the communication network such as the internet and mobile net develops, multimedia contents are expanding. Despite widespread use of digital multimedia data, there have been threats and attacks to information in communication systems. For this reason, information security becomes very important and necessary. In order to protect original information such as multimedia data, a number of electronic or optical cryptosystems have been proposed. One of the simple methods to ensure security is considering all data as binary strings and encrypting them using encryption algorithms such as DES(Data Encryption Standard) or AES (Advanced Encryption Standard). [1] Encryption is the process of transforming the plain data to the cipher data by a security key (such as a common key or a secret key) to ensure its security. In order for an authorized user to decrypt the cipher , the same correct security key has to be known to the authorized user. In conventional symmetric key cryptography, the security key is opened by all the users as a common key which is not transmitted to users. Therefore, this type of algorithm has a weak point against data interception by an unauthorized user. Since a security key is the core of most data cryptosystems, the protection of the security key is also very important. In general, when the multimedia data is static, it can be treated as binary data and the conventional electronic encryption methods can be used. However, these methods involve amounts of computations and are not fast enough for high-volume multimedia data. [2] Recently, various kinds of optical encryption techniques have been proposed for security systems because optical systems have merits of parallel processing and fast operation. [3-11] Among them the optical information is composed of complex function which is in phase and amplitude forms, and in order to get the complex encrypted data, a holographic recording technique may be required. This requirement makes it difficult to store and transmit the encrypted information over a digital network. However, optical encryption and decryption to record and reconstruct the complex values can be easily performed using a phase-shifting digital holographic technique. [13-16] Recently, we have presented some papers on the optical encryption using the phase-shifting digital holographic method. [17-22]

In this paper, we propose a dual optical encryption method for binary image data and secret key based on 2-step phase-shifting digital holography for a cryptographic system, and show the performance of the proposed system for dual cryptography. The encrypted Fourier transform hologram is obtained by phase-shifting a digital holographic technique from an optical setup based on a Mach-Zehnder type interferometer, which is a 256 gray level quantized digital hologram recorded by CCD. The encrypted digital hologram can be transmitted over a digital communication network. The decryption is carried out electronically by computer. In Section Ⅱ, the encryption and decryption technique with 2-step phase-shifting digital holography are described. In Section Ⅲ, computer experiments show results of the encryption and the decryption with the proposed method. Finally, conclusions are briefly summarized in Section Ⅳ.

The main idea in the proposed method to encrypt binary data is to make more highly secure encryption and decryption, which is accomplished by encrypting and transmitting the individual security key, called secret key or private key, and this encrypted security key is used to decrypt the original binary data. Input data to be encrypted is binary bit data or a binary image, and a gray-level optical image can be encrypted after processing the gray-level image into the digitized 8-bits binary data by an analog-to-digital ASCII encoding method. [20, 21]

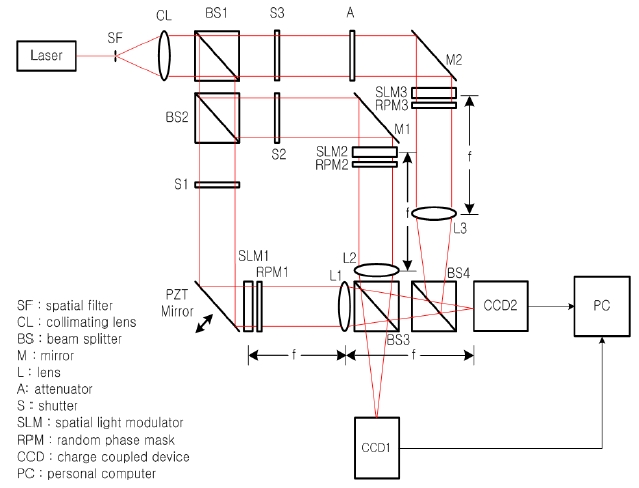
Figure 1 shows the optical setup for the dual optical encryption system for the binary data using the 2-step phase-

shifting digital holographic method, which is based on Mach-Zehnder interferometer architecture. Schematically, the optical setup contains two Mach-Zehnder interferometers. Beam splitters BS1 and BS2 divide collimated light into two plane waves as the reference and the object beams. With shutters S1, S2 open and S3 closed, the inner interferometer is operated for encrypting the secret (or private) key of the user with the common (or public) key. The collimating light after being reflected by the PZT mirror illuminates the spatial light modulator (SLM1) which displays the binary secret key to be encrypted. The output beam from SLM1 is multiplied by a random phase mask (RPM1), and is Fourier transformed on the charge coupled device (CCD1) by lens L1 as the object beam. The other collimating light by BS2 after reflecting on a mirror M1 illuminates the SLM2 which displays the binary common key code, resulting in Fourier transform on the CCD1 by lens L2 as the reference beam, where another random phase mask (RPM2) is multiplied with the SLM2. The random phase mask improves to widen the dynamic range of the Fourier transform in the spatial frequency domain on the CCD. With shutters S1, S3 open and S2 closed, the outer interferometer is operated for encrypting the information data such as binary data or image with the secret key. In this case, the light from SLM1 is operated as the reference beam, while the light from SLM3, RPM3 and L3 is operated as the object beam. In this path, an attenuator(A) is used for controlling the reference-to-object beam ratio properly for acquiring a vivid interference pattern. The interference pattern from these two Fourier transformed beams is recorded on the CCD2.

In the previous papers [19, 22], we described the encryption and decryption principle by using the 2-step phase-shifting digital holographic method.

Let |s(x,y)| be a binary secret key to be encrypted and exp[jθ_s(x, y)] be a random phase pattern, where x and y are transversal coordinates at the input spatial plane. The multiplication of the two is represented as

Fourier transform of s(x, y) is expressed as

where α and β are transversal coordinates at the spatial frequency plane.

Let |c(x,y)| be a binary common key and exp[jθ_c(x, y)] be anot her random phase pattern. The multiplication of the two is represented as

Fourier transform of c(x,y) is expressed as

Then, the digital holographic intensity pattern recorded by the CCD1 at the spatial frequency plane is given by

with the object beam and the reference beam given by Eqs. (2) and (4), where Δ？_SC = ？_S? ？_C is the phase difference between the object and the reference beams. The phase-shifting interferometry method gives the exact reconstruction of the phase difference between the object and the reference beams and amplitude of these two beams. Two intensity patterns in the form of digital holograms are achieved by 2-step phase-shifting digital holography with the reference beam phase shifted by 0 or π/2. The PZT mirror can allow phase shift with phase steps of π/2 by moving the mirror properly. This 2-step phase-shifting digital holography has a merit of the reduced number of holograms compared to multi-step phase-shifting holography. By rewriting Eq. (5), 2-step phase-shifting digital holograms are represented as

These two digital holograms are encrypted data, which are stored in a computer and transmitted through the digital communication network.

After DC-term removal technique is applied to Eq. (6), the phase difference of object beam and reference beam and the magnitude are calculated as follows. [22]

where I₁' and I₂' are modified holographic intensities after DC-term removal.

From Eqs. (7) and (8), the complex hologram1 with secret key encryption information is expressed as

Similarly, we can encrypt binary data or image with the secret key. Let b(x, y) be binary data or image to be encrypted and exp[jθ_b(x, y)] be a random phase pattern. The multiplication of the two is represented as

The Fourier transform of b(x, y) is expressed as

Then, the digital holographic intensity pattern recorded by the CCD2 at the spatial frequency plane is given by

with the object beam and the reference beam given by Eqs. (11) and (2), where Δ？_BS = ？_B? ？_S is the phase difference between the object and the reference beams.

After carrying out the 2-step phase-shifting digital holographic method, the phase difference of object beam and reference beam and the magnitude are acquired as follows.

where I₃' and I₄' are modified holographic intensities after DC-term removal.

From Eqs. (13) and (14), the complex hologram2 with data encryption information is expressed as

In order to get the complex distribution B(α , β) and decrypt the original binary data or image, we need the complex distribution S(α , β) of the secret key. Note that it is possible to get S(α , β) by Eq. (9) with knowledge of the complex hologram1 because the Fourier transform pattern of the secret key, Eq. (4), is acquired by the opened and known binary common key code of c(x, y). We need the intensity distribution |C(α, β)|² of the common key in order to reconstruct S(α , β). This intensity |C(α, β)|² is acquired when we get the DC-term information on the CCD1 by removing the object beam in the optical setup shown in fig. 1, which is done by closing the shutter S1, S3 and opening the shutter S2 only. And we also need the intensity distribution |S(α, β)|² of the secret key in order to reconstruct B(α , β). Similarly, the only object beam intensity recorded on the CCD2 gives |S(α, β)|² by closing the shutter S1, S2 and opening the shutter S3 in the optical setup shown in fig. 1. Using the complex hologram1, hologram2 and the common key, the reconstructed complex

distribution is obtained by

By using an inverse Fourier transformation, the original data information is reconstructed and the original binary data or image is decrypted after carrying out the proper threshold.

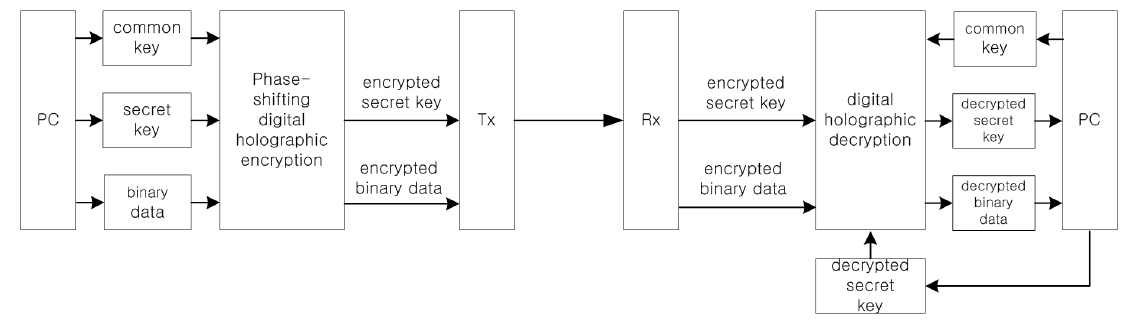
Figure 2 shows block diagram of dual encryption and decryption procedure.

We show the performance of the proposed dual optical encryption method by computer simulations. The binary bit code of size 256×256 pixels shown in Fig. 3(a) is used as the common key which is random generated for convenience, and the binary images(Girl1 and Girl2) of size 256×256 pixels shown in Fig. 3(b) and (c) are used as the user’s secret keys to be encrypted, respectively. These secret keys can be interpreted as the user’s own watermark images for authentication cryptography. The binary image data of size 256×256 pixels shown in Fig. 3(d) is used as input data to be encrypted by the user’s secret key.

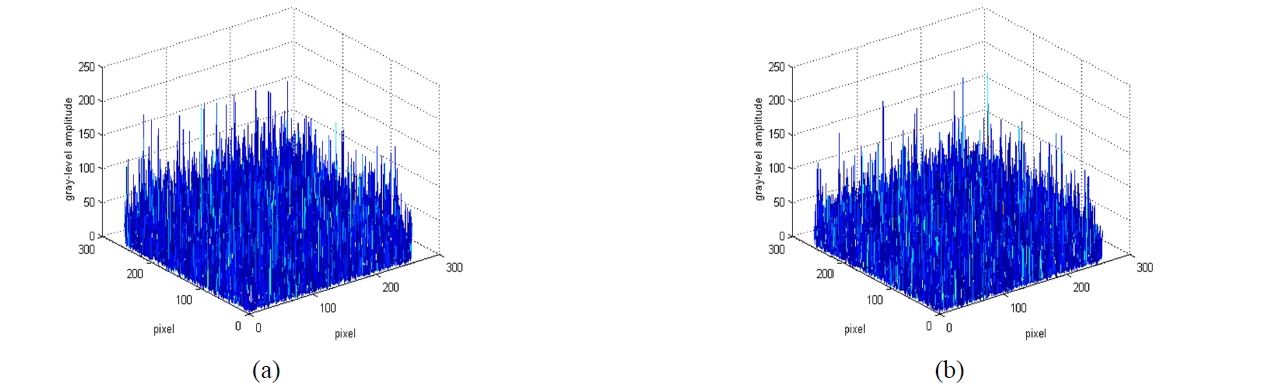
Figure 4 shows an example of the encrypted digital holograms which are recorded on CCDs. Each hologram is quantized with 256 gray levels. The histogram of the encrypted secret key1 shown in Fig. 4(a), which has a uniform and random gray-level distribution, is the one of the acquired 256 gray level histogram patterns using 2-step phase-shifting digital holography. Similarly, Fig. 4(b) shows the one of the acquired 256 gray level histogram patterns of the encrypted binary image using 2-step phase-shifting digital holography.

From the complex holograms calculated by the retrieved phase and amplitude from the encrypted data, reconstruction and decryption of the encrypted secret key and the encrypted image are carried out successfully. For example, Fig. 5(a) shows the reconstructed secret key1 image pattern when the correct common key is used for the secret key decryption. Fig. 5(b) is the decrypted binary image(Girl1) after binarization with the proper threshold. The decrypted binary image is the exact same original secret key1 image and

has no error when the same correct common key is used for decryption. This secret key can also be interpreted as watermark of the user1. Fig. 5(c) shows the phase map representation of the Fourier transform of the reconstructed secret key1 by the reconstructed complex hologram1 and the common key.

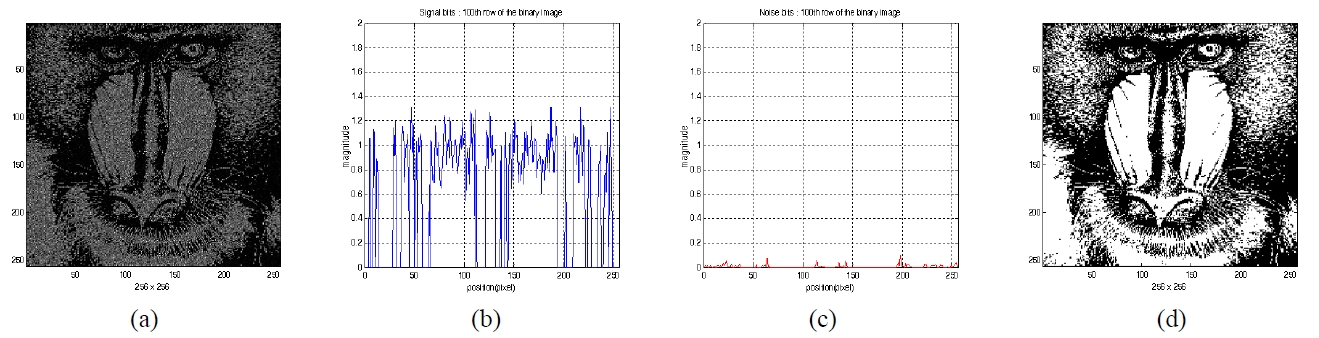
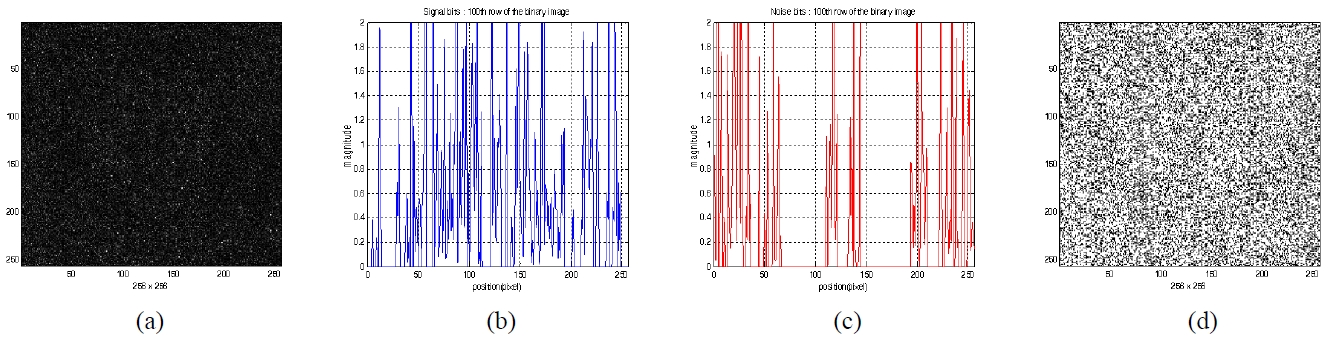
Figure 6(a) shows the reconstructed image pattern when the secret key1 of user1 is used for the encrypted hologram2 which is encrypted by the secret key1. We investigated the distribution of the pixel magnitude of the reconstructed image pattern and signal-to-noise ratio. One of the cross sections in the reconstructed image is shown in Fig. 6(b) and (c). The magnitude of the signal bits(one value in the original image) is about 1 in Fig. 6(b), but the magnitude of the noise bits(zero value in the original image) is below about 0.2 in Fig. 6(c). Since the magnitude of the signal

bits is much greater than the magnitude of the noise bits, the reconstructed image can be decrypted into the original image when the proper threshold value is well defined. Fig. 6(d) is the decrypted binary image after binarization with the proper threshold value of 0.3. The decrypted binary image is the exact same original image data and has no error when the same correct secret key1 is used for decryption.

Figure 7(a) shows the reconstructed image pattern when the secret key2 of user2 is used for the encrypted hologram2 which is encrypted by the secret key1. This reconstructed pattern has a different intensity pattern(i.e. random pattern) compared to the one shown in Fig. 6(a). We also investigated the magnitude distribution of the cross section in the reconstructed image and signal-to-noise ratio. Fig. 7(b) and (c) show the results. Since the magnitude of the noise bits of some pixels are greater than the magnitude of signal bits, the proper threshold value cannot be defined. Therefore, the reconstructed image cannot be decrypted into the original image. Fig. 7(d) is the decrypted binary image after binarization with the same threshold value of 0.3.

We propose a new dual optical encryption method for binary data and secret key based on 2-step phase-shifting digital holography for a cryptographic system. Dual optical encryption is implemented by constructing two Mach-Zehnder type interferometers simultaneously. The inner interferometer is used for encrypting the secret key with the common key, while the outer interferometer is used for encrypting the binary data with the same secret key. This proposed dual optical encryption method provides a more advanced cryptosystem to use double encryption in the binary data and has advantages of compactness and easy configuration of the optical system. For the case of applying the proposed method to encrypt a binary image data with a secret key image, a highly secure encryption is achieved. Computer experiments verified that the proposed method is perfect and suitable for cryptographic applications and secure communication systems.