Optimal transfer trajectories based on the planar circular restricted three body problem are designed by using mixed impulsive and continuous thrust. Continuous and dynamic trajectory optimization is reformulated in the form of discrete optimization problem. This is done by the method of direct transcription and collocation. It is then solved by using nonlinear programming software. Two very different transfer trajectories can be obtained by the different combinations of the design parameters. Furthermore, it was found out that all designed trajectories permit a ballistic capture by the Moon’s gravity. Finally, the required thrust profiles are presented and they are analyzed in detail.
In Moon exploration, the designs of the thrust system and considerations of the transfer orbit that is required for the Earth-Moon transfer, must take precedence. In general, a Moon exploration spacecraft must make a series of maneuvers and they are composed of trans-lunar trajectory injection, trajectory correction maneuvers and lunar orbit injection, in that sequence[1]. The nature of this series of maneuvers is determined by the type of the launch vehicle and the onboard spacecraft rockets. Consideration of the characteristics of the thrust system is essential for designing a transfer trajectory. In general, thrust systems are classified as impulsive thrust or continuous thrust. The solid rockets that use impulsive thrust are not able to control the thrust magnitude or the combustion time whereas liquid rockets that use continuous thrust can. The most general methods for transfer trajectory design using multiple impulsive maneuvers[2, 3] are the Hohmann transfer, Bi-elliptic Transfer, Weak Stability Boundary(WSB)[4, 5] that consider the possibility of the reignition of the rocket. Recently, research has progressed in the transfer trajectory design which actively uses electronic and ion thrusters. However, transfer trajectories with a spiral shape have a disadvantage that the flight time takes dozens to hundreds of days[6, 7] when using low thrusters that work successively for long periods. The most effective Earth-Moon orbit transfer in terms of fuel consumption is the use of a natural orbit that takes the advantage of the attractions of the Earth and the Moon. Until now, large effort has been taken to look for a natural orbit that is based on the circular restricted three body problem (CRTBP) called as the low energy orbit[5]. The research to look for this orbit numerically by using weak boundary stability (WBS) or invariant manifold theory is now mature[4, 8].
Pierson and Kleuver[1] found out minimum-fuel planar trajectories from a circular low Earth parking orbit (LEO) to a circular low lunar parking orbit (LLO). The optimal low-thrust transfer problem studied in the classical CRTBP is solved by formulating and successively solving a hierarchy of subproblems. This results in a three stage approach. Kleuver and Pierson[9] extended their work on optimal planar transfers to a minimum fuel problem for a three dimensional transfer by using a hybrid method. They also obtained minimumfuel, two-dimensional and three-dimensional, Earth-Moon trajectories for a nuclear electronic propulsion spacecraft with relatively low thrust-to weight ratio[10]. Herman and Conway[11] found out an optimal, low thrust, Earth-moon orbit transfers with nonlinear programming for the case where the initial spacecraft Earth orbit is arbitrary and the Moon is in its actual orbit. The transfer time is relatively long (in the order of 30 days) but it is minimized. Belbruno and Miele[12] proposed a method for a low energy Earth to Moon transfer trajectory design by using WSB. Its transfer trajectory enters the Moon mission orbit and it can carry out a natural capture or so called “ballistic capture”. Koon et al.[6] considered the coupled three body problem as a precursor to higher fidelity gravitational models. They constructed low energy Earth to Moon transfer trajectories that execute a ballistic capture by the Moon, using the invariant manifolds of the periodic orbits.
The optimization problems that are solved to find the transfer trajectories are classified as either direct or indirect methods. Indirect methods may exhibit rapid convergence and when compared to a direct method, it requires fairly fewer function computations. Due to these advantages, much early optimization research was focused on the indirect methods and these methods were successfully demonstrated in several low-thrust problems[13-15]. However, indirect methods also have disadvantages due to the initialization difficulties for the adjoint variable of the TPBVP, the sensitivity of Euler- Lagrange equation, and discontinuity. On the other hand, direct methods convert the calculus of the variation problem into a parameter optimization problem that minimizes the performance index by using nonlinear programming (NLP). It also transcribes the states and controls through direct transcription and collocation[16, 17] or differential inclusion[18, 19]. The entire trajectory to be optimized by this direct method is represented in terms of nodes[17], and a large number of design variables.
This study proposes an optimal Earth-Moon transfer trajectory design method that uses a mixed impulsive and continuous thrust, by employing direct transcription and collocation method. The transfer time can be reduced significantly by using the mixed impulsive and continuous thrust. Impulsive thrust contributes to the escape of spacecraft from the Earth’s gravity field. Continuous thrust contributes to the translunar trajectory and the Moon mission orbit insertion or capture. The Earth-Moon transfer trajectory is governed by the planar circular restricted threebody problem (PCRTBP) by considering the attractions of the Earth and the Moon simultaneously. Unlike Pierson and Kleuver’s three stage approach, this study does not consider a hierarchy of sub-problems that are categorized into three stages. Instead, continuous, dynamic trajectory optimization for every stage is reformulated in the form of a discrete optimization problem by using the method of direct transcription and collocation.
Various types of Earth-Moon transfer trajectories are then designed by adjusting the design parameters such as the relative weighting factor for impulsive and continuous thrust and flight time. We show the various types of transfer trajectory that escape the Earth’s gravitation and enter a translunar trajectory. This study shows that a transfer trajectory design is possible which meets the condition of a non-thrust orbit insertion or a so called ballistic capture, that is, the spacecraft is placed in the Moon mission orbit by the Moon’s gravity alone. Furthermore, we show in detail the required thrust magnitude and transfer trajectory types corresponding to various Earth-Moon transfer trajectory designs.
2. PLANAR CIRCULAR RESTRICTED Three body PROBLEM
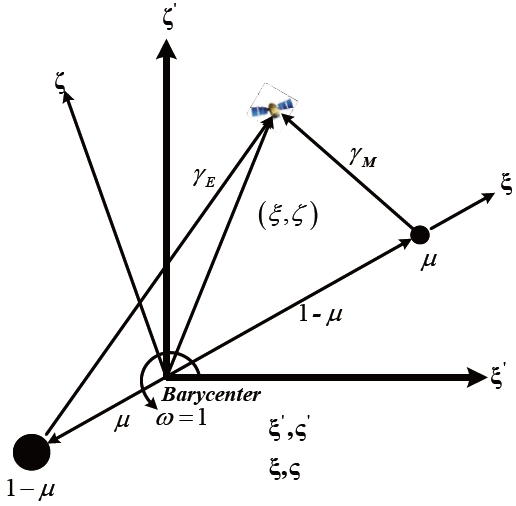
The design of the Earth-Moon transfer trajectory can be understood through the three-body orbit dynamic modeling that considers the attractions of both the Earth and the Moon. This study employs the PCRTBP which is described in the Earth-Moon plane. The binary system that is composed of the Earth and the Moon, as seen in Fig. 1, is assumed to rotate with an angular rate ω about the barycenter. As a more detailed derivation of the circular restricted three-body problem equations can be seen in References 20 and 21, the necessary equations that consider only the planar motion are briefly described below:
Where,
μ : Mass ratio of the restricted three-body problem
γE = √(ξ+μ)2+ζ2 : Earth-satellite distance
γM = √(ξ?1+μ)2+ζ2 : Moon-satellite distance
and (uξ, u?) represents the control acceleration. It should be noted that Eqs. (1) and (2) are written in a non-dimensional form. Distance unit (DU) is the distance between the Earth and the Moon, 3.844×105km, and the time unit (TU) is the Moon’s period divided by 2π. Thus, the velocity unit (VU) is DU/TU and the acceleration unit (ACU) is DU/TU2.
3. Problem formulation for Earth-Moon Optimal TRANSFER TRAJECTORY
3.1 Mixed Impulsive and Continuous Thrust
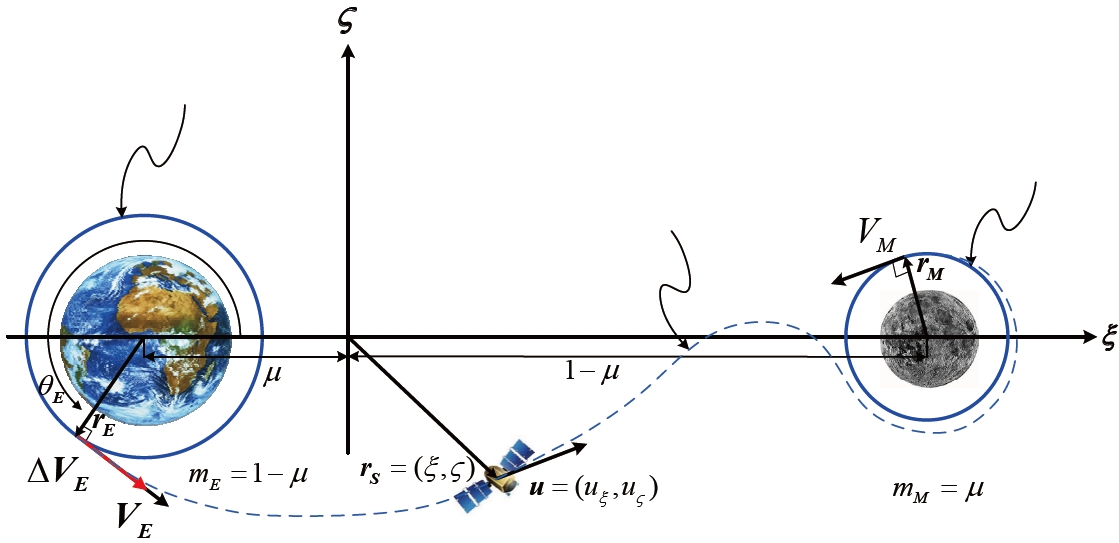
In a broader sense, the Earth-Moon transfer trajectory is an orbit transfer from an Earth orbit to a Moon orbit. Hohmann and bi-elliptic transfers are the representative orbit transfer methods that use impulsive thrust in the tangential directions. Hohmann and bi-elliptic describe an insertion into an Earthcentered Moon orbit. In order to insert the spacecraft into a Moon-centered mission orbit, an impulsive maneuver is required at the intersection point of the Earth-Moon transfer trajectory and the Moon-centered mission orbit. Moreover, there is a different type of orbit transfer method that uses continuous thrust. The ESA Smart-1 spacecraft launched in 2003 is a successful example for using continuous thrust from a solar electric propulsion system. The transfer trajectory was the one that departs from the Earth’s parking orbit and reaches the Moon mission orbit by gradually extending the transfer trajectory. This is appropriate for the transport of all sorts of exploration equipment and payloads because the fuel consumption is very less. Moreover, this type of transfer method using a low thrust system may take several months or years to reach the Moon mission orbit
This study employs mixed impulsive and continuous thrust in order to exploit the characteristics of them and to out find an Earth-Moon optimal transfer trajectory design. As a result, the transfer time that may take hundreds of days
by different methods can be reduced by using the mixed impulsive and continuous thrust. Furthermore, it is desired that the additional Δ
Where, Δ
is the required continuous thrust magnitude during the transfer period, α is the weighting factor that determines the relative contribution from the impulsive and continuous thrust, and
Referring to Fig. 2, this study assumes that the satellite departs from the circular parking orbit of radius
Where,
is the spacecraft speed in the Earth parking orbit and the phase angle, θE determines the departure position. Hence, the design variables in the Earth departure are the velocity increment, Δ
In this study, it is preferred that the spacecraft is inserted
into a circular Moon-centered orbit with radius,
Where,
denotes the orbital speed in the Moon mission orbit. It should be noted that no additional impulse was used apart from the one used during Earth departure.
3.4 Transfer Trajectory Condition
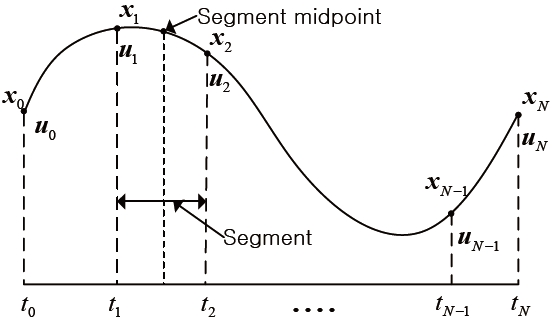
During the Earth-Moon transfer, the spacecraft should obey the dynamic equations that are given by Eqs. (1) and (2). Here, the purpose is to find out the control acceleration (uξ, u?) that not only minimizes the performance index defined in Eq. (3) but also makes the spacecraft satisfy the Moon arrival condition at the final time. In order to solve the optimization problem in this work, the direct method based on direct transcription and collocation that transcribes the optimization problem to NLP is applied. For this purpose, the continuous design variables along time, t as seen in Figure 3 are considered as discretized N nodes. The individual time points are called as node or grid points. Therefore, the design variables are defined as follows.
Where,
Moreover, the performance index by considering the discretized design variables is slightly modified as follows,
It should be noted that the state variables
Where,
Where, y is the state vector at the segment midpoint and
4. OPtimal transfer trajectory design results and analysis
4.1 Direct vs. Spiral Departure Trajectory Design Example
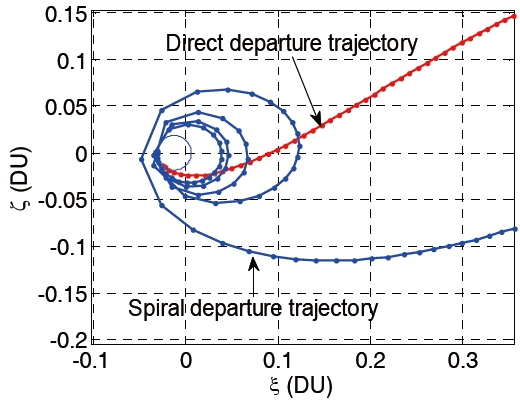
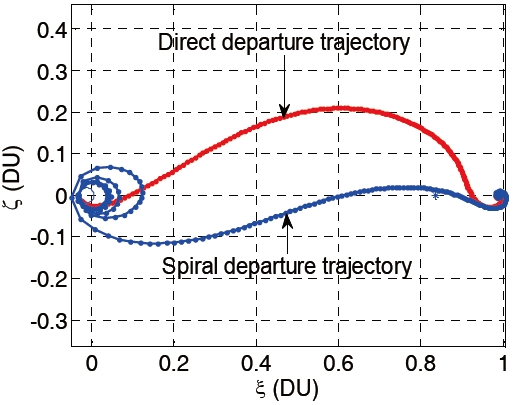
Figures 4 and 5 shows the representative examples of Earth- Moon transfer trajectories that are obtained in this work. One may easily note that the shape of the trajectories at the Earth departure phase is quite different in the sense that whether a spacecraft is directly injected into the translunar trajectory or it follows the spiral path by elevating the altitude gradually. We call the former one as a direct departure trajectory, and the latter one as a spiral departure trajectory. Various trajectories can be obtained by the different combinations of design parameters, that is, the relative weighting factor, α and the flight time,
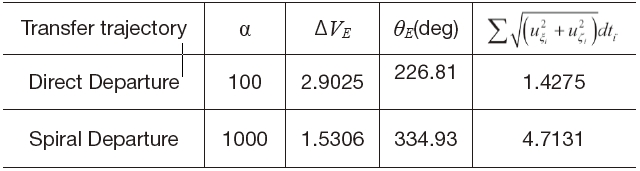
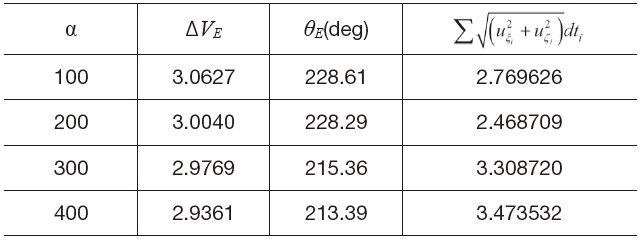
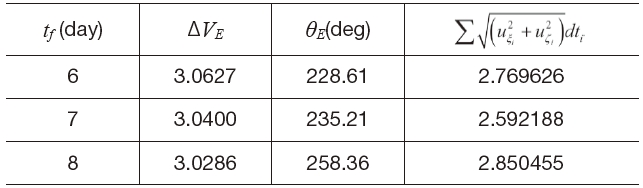
Table 1 shows the features of direct departure and spiral departure trajectories. In this example, the used flight time is 6 days. It is obvious that the relative weighting factor α determines the type of Earth departure trajectory. The impulsive velocityΔ
for the direct departure trajectory and it is smaller than that for the spiral departure trajectory.
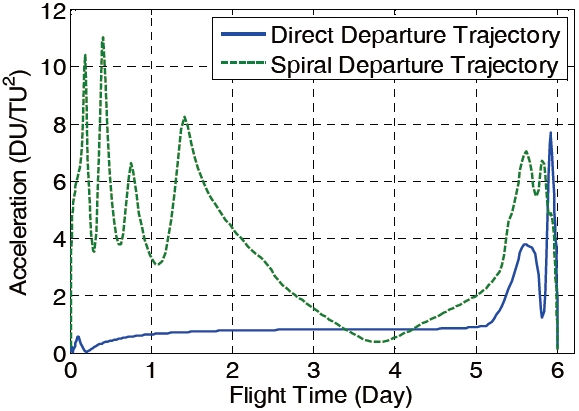
Figure 6 presents the time histories of the required
[Table 1.] Earth-Moon Optimal Transfer Trajectory Results.
Earth-Moon Optimal Transfer Trajectory Results.
continuous thrusts for both of the transfer trajectories during the flight time of 6 days. The direct departure trajectory requires relatively smaller continuous thrust compared to the spiral departure trajectory. It should be noted that the magnitude of continuous thrust approaches zero. This implies that the so-called ballistic capture is achieved at the Moon arrival phase.
As mentioned previously, very different transfer trajectories can be designed by using the different combinations of the relative weighting factor and the flight time. As one of the objectives of this study is to find out an Earth-Moon transfer trajectory with reasonable flight time and smaller impulsive thrust requirement, it is important to study the effects of design parameters on the final results. The other consideration in this kind of numerical search for the optimal solution is to get a decent initial guess for iteration. Moreover, the altitude of the departure and arrival orbits is an important factor that determines the numerical convergence. As such, this study applied the progressive homotopy-like[22] an optimization method. For example,
once an optimal trajectory has been obtained, this result is used as an initial guess for a new problem that has slightly different departure/arrival altitude, the relative weighting factor, and the flight time.
Relative Weighting Factor
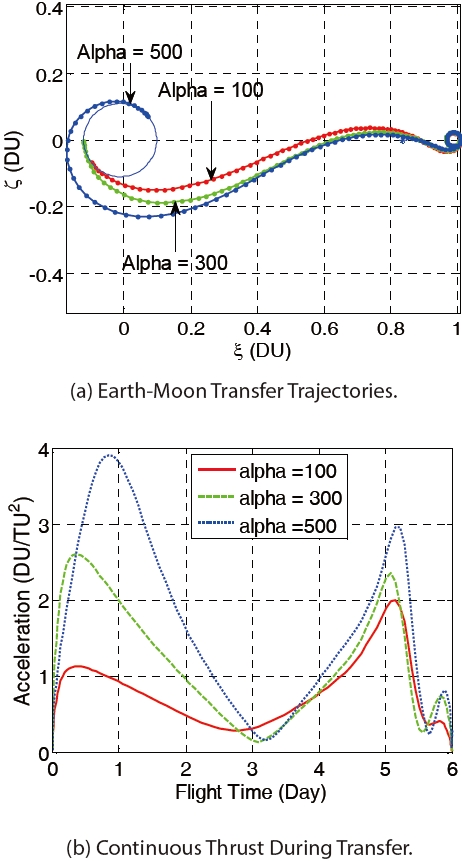
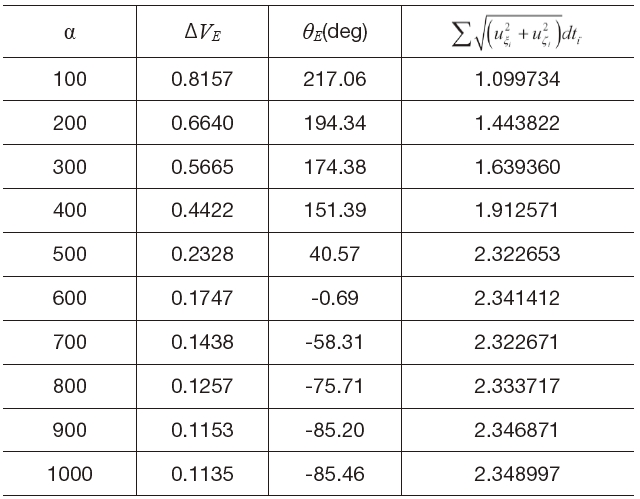
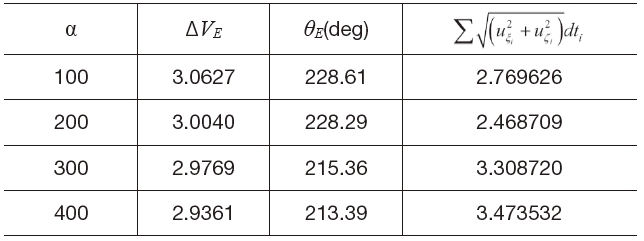
For a fixed flight time of 6 days, the weighting factor α determines the shape of the departure trajectory regardless of the altitude of departure and arrival orbits. Figures 7 shows the Earth-Moon transfer trajectories and the required continuous thrusts during the transfer from the high altitude Earth departure orbit to the high altitude Moon arrival orbit with a flight time of 6 days. The weighting factors used are 100, 300, and 500, respectively. As the relative weighting factor α gets larger, the spacecraft immediately enters the translunar trajectory but it requires a larger continuous thrust during transfer. Table 2 supports this tendency clearly. From Fig. 7(b), it can be seen that the continuous thrust magnitude becomes very small at the end of flight. This implies that the spacecraft is captured by the Moon gravity in a so-called ballistic manner.
For a low altitude departure and arrival case, the relative weighting factor α has a significant effect on the shape of the transfer trajectory at the vicinity of the Moon and this can be seen from Fig. 8. In this example, the altitude of both the departure and arrival orbits was set to 100 km. In contrast to the case of transfer between high altitude departure and arrival orbits, the relative weighting factor does not seem to cause much variations in the Earth departure trajectories. On the other hand, it alters the trajectory shape at the Moon arrival phase and this can be seen from Fig. 8(b). Figure 8(c) shows the required continuous thrust during a transfer.
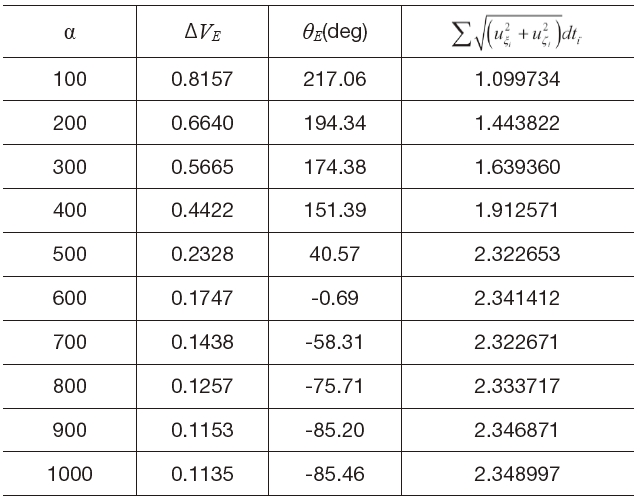
Summary of Parametric Study Results (High Altitude Earth-Moon Transfer, Direct Departure Trajectory, Parameter: Weighting factor).
Moreover in this case, the continuous thrust also approaches zero as it enters the arrival orbit. From the results that are summarized in Table 3, the relative weighting factor does
Summary of Parametric Study Results (Low Altitude Earth-Moon Transfer, Direct Departure Trajectory, Parameter: Weighting factor).
Summary of Parametric Study Results (Low Altitude Earth-Moon Transfer, Spiral Departure Trajectory, Parameter: Weighting factor)
not significantly affect the velocity increment requirement for departure.
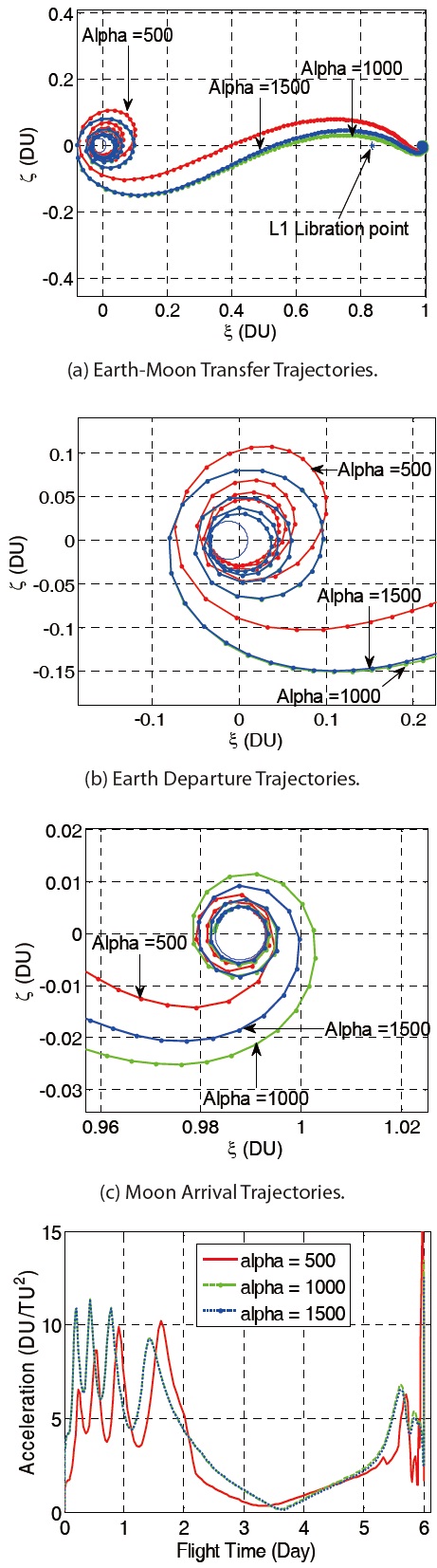
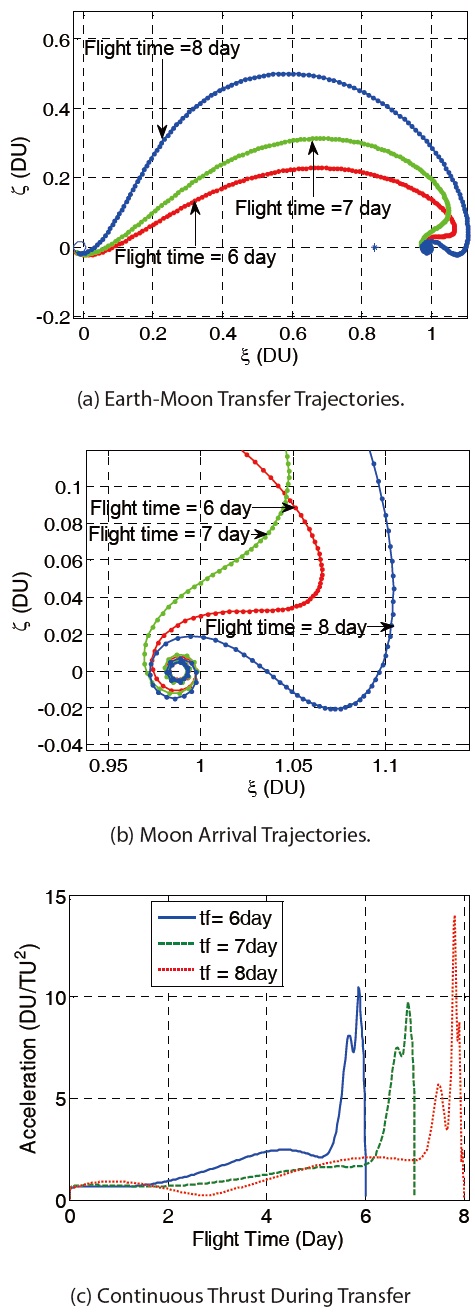
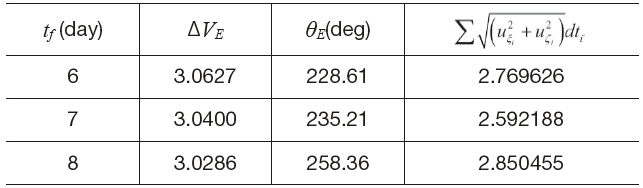
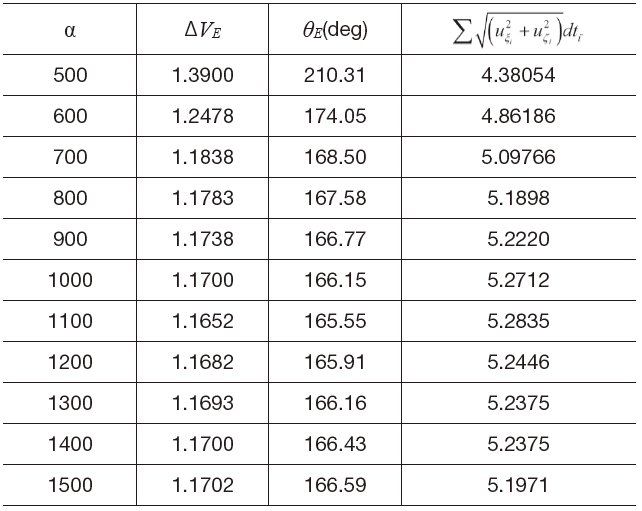
Figures 9 shows the Earth-Moon transfer trajectories and the required continuous thrusts during transfer from the low altitude Earth departure orbit to the low altitude Moon arrival orbit with a flight time of 6 days. The used weighting factors are 500, 1000, and 1500, respectively. As the relative weighting factor α gets larger, the Earth-Moon transfer trajectories get closer to that libration point, L1 and it is similar to each other in the shape of an Earth-Moon transfer trajectory. Moreover, the required continuous thrust during transfer gets larger whereas the impulsive thrust gets smaller. The relative weighting factor α does not have a significant effect on the shape of the Earth-Moon transfer trajectories when it is larger than 1000. Table 4 supports this tendency clearly. The values of the impulsive thrust for the low altitude spiral departure in Table 4 are comparatively smaller than the values of impulsive thrust for the low altitude direct departure which is shown in Table 3. As a result, the spiral departure trajectory contributes to the small size of the launch vehicle by reducing the impulsive thrust.
Flight Time
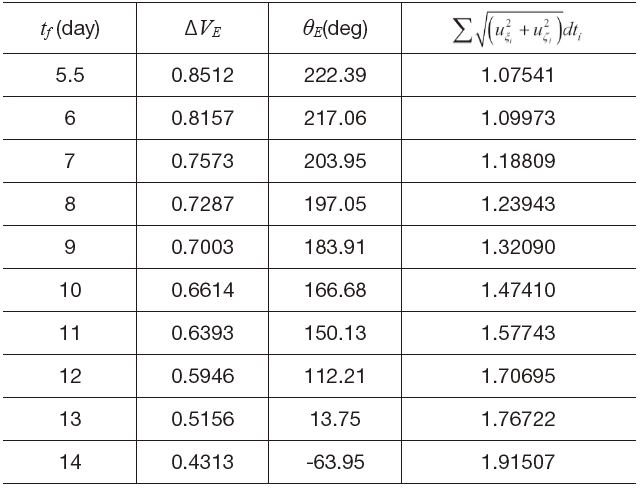
For the varying flight time, the Earth-Moon transfer trajectories are designed for the high and low altitude direct departures, and the low altitude spiral departure trajectory. For the high altitude departure and arrival case, the flight time
For the low altitude departure and arrival case, the flight
Summary of Parametric Study Results (High Altitude Earth-Moon Transfer, Direct Departure Trajectory, Parameter: Flight Time).
time
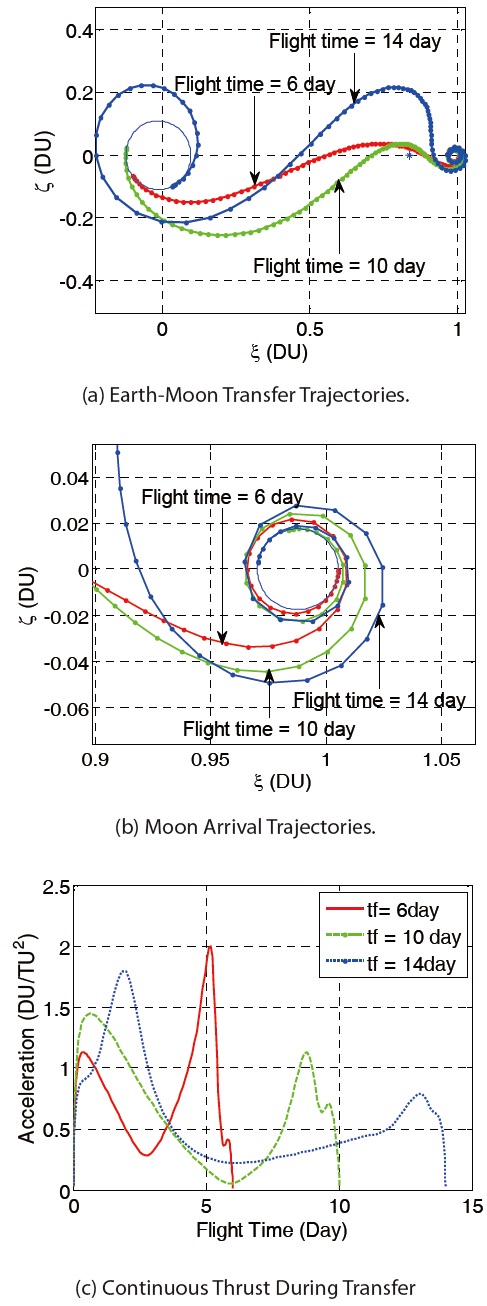
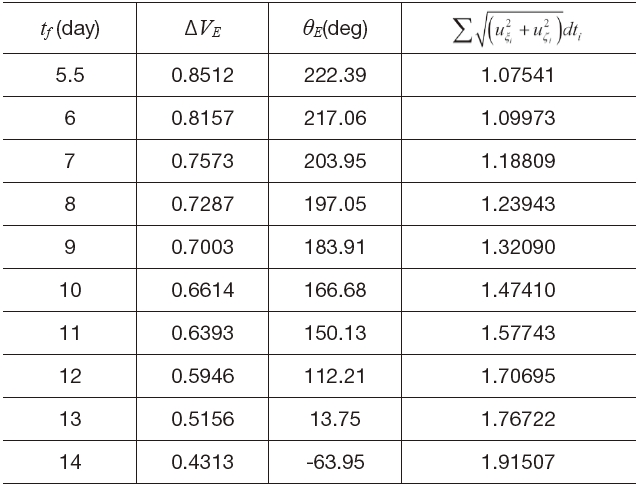
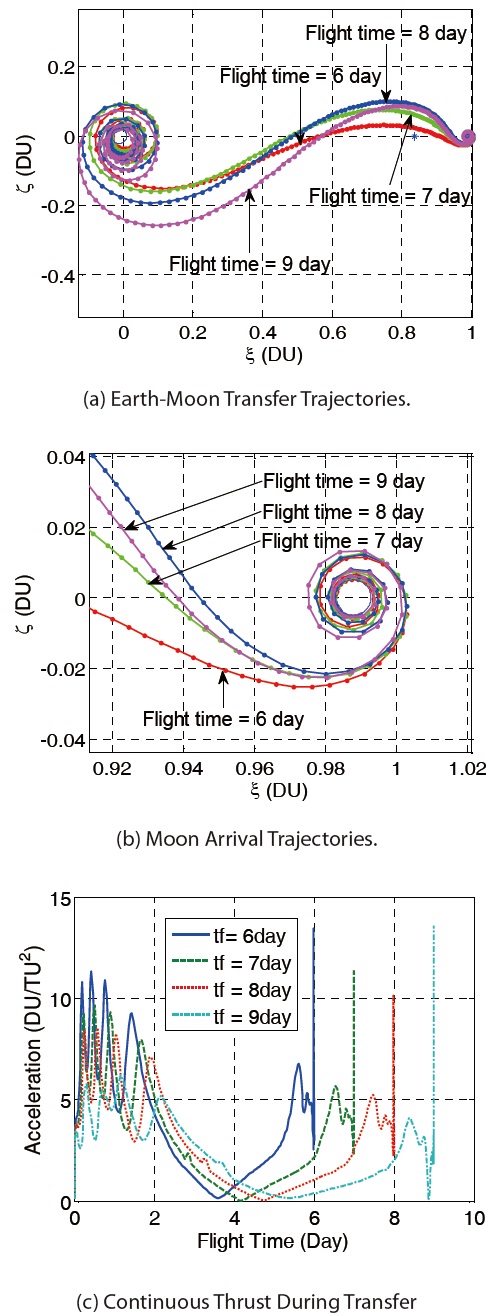
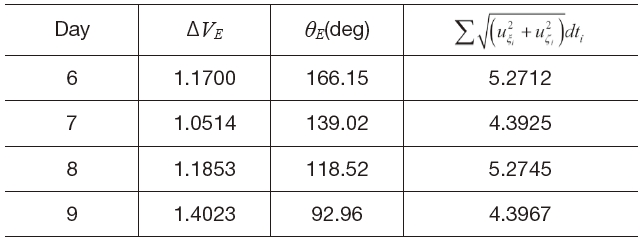
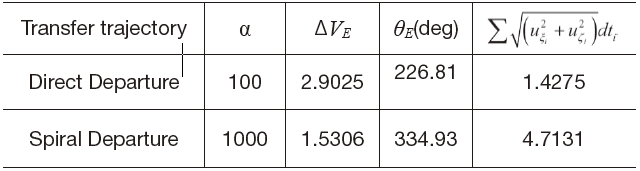
Figures 12 shows the Earth-Moon transfer trajectories from the low altitude Earth departure orbit to the low altitude Moon arrival. The used flight times are 6, 7, 8 and 9 days, respectively. As the flight time gets longer, it is obvious that the Earth departure trajectories tend to disperse further away from the Earth. Moreover, the flight time has a significant effect on the velocity increment requirement for departure. This is due to the spacecraft drifts in the Earth-Moon transfer trajectory by natural attraction after it escapes the Earth’s gravitational field with a big thrust, to meet the required flight time condition. Figure 12(c) shows the required continuous thrust during transfer. From the results that are summarized in Table 7, the flight time has a significant effect on the velocity increment requirement for departure. The flight time taken for the Earth-Moon transfer trajectory is an important factor to determine the performance requirements
Summary of Parametric Study Results (Low Altitude Earth-Moon Transfer, Direct Departure Trajectory, Parameter: Flight Time).
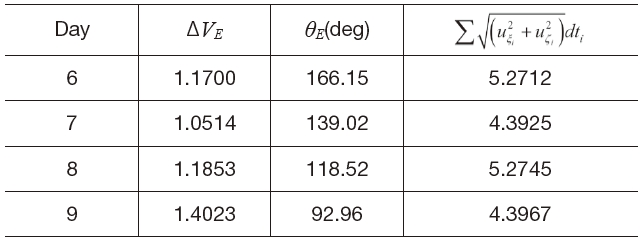
Summary of Parametric Study Results (Low Altitude Earth-Moon Transfer, Spiral Departure Trajectory, Parameter: Flight Time).
of the on board thruster in the spacecraft. If a very short flight time is required for the Earth-Moon transfer then, naturally a bigger impulsive or continuous thrust is required but such a launch vehicle is impractical. On the contrary, if a very long flight time is required then, there is a problem that requires a higher launch vehicle performance. The spacecraft should waste a certain time in order to fit the phase of the Moon with respect to the Earth. The practical problem in going to the Moon involves a rendezvous problem with the Moon a certain time after departing from the Earth. Consequently, the flight time
In this paper, results of the Earth-Moon transfer trajectory studies are presented. Planar, circular, restricted three body formulation is adopted to represent the system dynamics. Usage of mixed thrust, that is, impulsive thrust at Earth departure, continuous thrust during Earth-Moon transfer and Moon capture is assumed. This continuous and dynamic optimization problem is reformulated as a discrete optimization one by using the method of direct transcription and collocation. Then, it is solved by using the nonlinear programming software. As a performance index, we choose to use the sum of the initial Δ