Surface tension (γ) is a type of force caused by unbalanced molecular attraction on a liquid surface; it has effects in all dimensions. The direction of surface tension is tangent with the liquid surface, and is vertical to the division line of the two phases. If the liquid surface is planar, the surface tension is right on this plane. On the other hand, if the liquid surface is a curved one, the surface tension is on a tangent plane [1]. Cohesive energy density (
where V is the molar volume of the substance.
This equation is only suitable for non-associated small molecular systems; it is not suitable for large molecular systems with hydrogen bonds [3]. Therefore, a new equation, suitable for both systems, is necessary.
In this study, a new model and the resulting equation for monomer coagulation are suggested in order to obtain a promising relationship between γ and
Fig. 1 shows a new schematic model of the surface tension between monomers during coagulation in a bath.
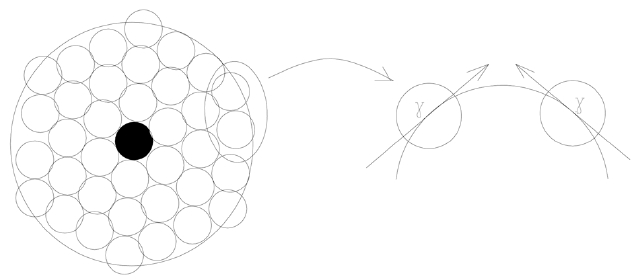
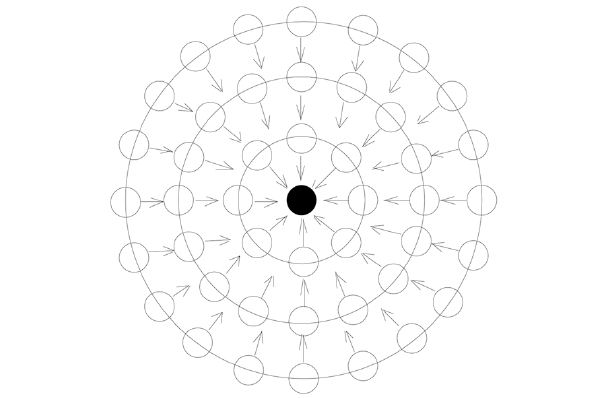
Because surface tension (γ) has a close relation with molecular weight (M), we introduce a new concept, shown in Fig. 1, to establish a comparable relation between monomers. The scale value of the surface tension (γ/M), defined by the surface tension per unit of molecular weight, can be applied to determine the relationship between the surface tension and the cohesive energy density. This scale value of surface tension is related to the lateral tension of the surface molecules, which in turn is related to the cohesive energy inside the liquid [1]. The scale value of the surface tension increases with the increase of the cohesive energy density, as shown in Eq. (1). Cohesion between molecules is the main source leading to surface tension. Suppose there is a liquid droplet and its volume and surface area tend to be minimized due to the cohesion and surface tension. Droplet monomers can be coagulated layer after layer from the center to the surface, as shown in Fig. 2.
The above model can be divided into the following processes and can be applied for the precipitation polymerization of acrylonitrile in coagulation bath solvent.
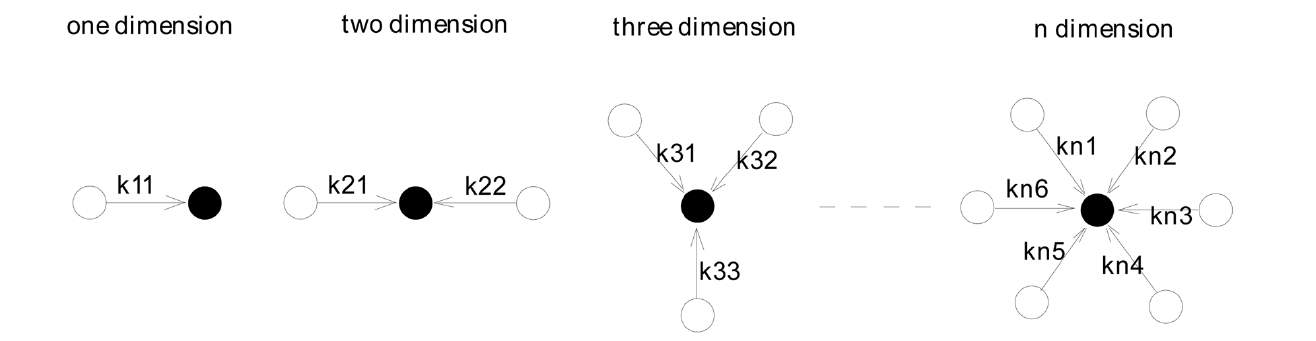
Suppose N is the concentration of nascent coagulates at time T; it then can be noted as [N], and the reaction constant of the core monomer and the other monomers can be noted as kij, in which i represents the dimension, and j refers to the serial number of monomers, as shown in Fig. 3.
Then, the following hypothesis can be suggested. F(N) is the number of coagulated monomers in the multi-dimensional direction in the precipitation polymerization. When the nascent monomer coagulates with another monomer, F(N) will be proportional to [N], as shown in the following equation.
When the nascent precipitation monomer coagulates with two other monomers, F(N) will be proportional to the square of [N], and the coagulation rate constant of the second monomer will be half that of the first monomer in its contribution to coagulation. Therefore, F(N)2 can be expressed as the following equation.
When the nascent precipitation monomer coagulates with three other monomers, F(N) will be proportional to the cube of [N], and the coagulation rate constant of the third monomer will be one-third that of the first monomer in its contribution to coagulation.
When the nascent precipitation monomer coagulates with n other monomers, F(N) will be proportional to [N]n, and the coagulation rate constant of the nth monomer will be one-nth that of the first monomer in its contribution to coagulation.
If there was no monomer to coagulate,
Therefore, all the coagulated nascent monomers will be the summation of F(N)1+ F(N)2 ----- + F(N)n, and the relationship between F(N) and [N] can be obtained as follows.
If each nascent precipitation monomer has the same ability for precipitation and
This equation is exactly part of the Taylor series
And, the total number of coagulated nascent precipitation monomers is
where Q is the quantity of precipitates (%), K1 is the constant, and K2 is reaction rate constant.
It is obvious that there is a natural progression relationship between the total number F(
And since F(N) is related to γ/M, the following equation can be obtained.
This is equivalent to the phenomenological concept: with the cohesive energy density changing, the scale value of the surface tension is proportional to its value:
In the abovementioned formula, A0 and K0 are constants concerning molecule structure [5].
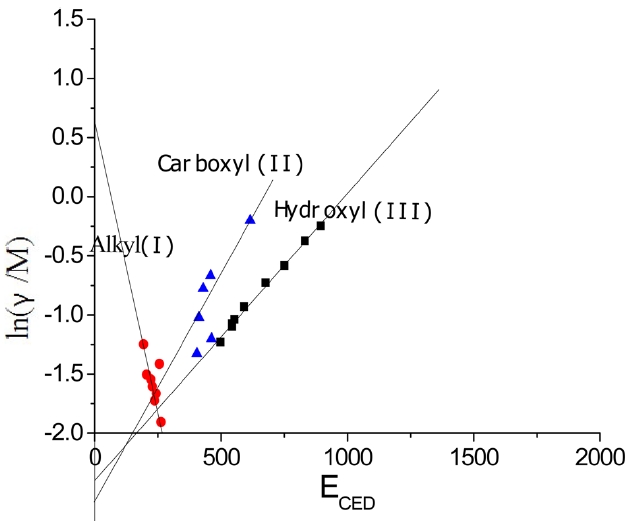
The surface tensions and cohesive energy densities of some organic materials that can be used as coagulation bath solvents were obtained from Mark [6]; these values are listed in Table 1. Data were applied to Eq. (13) and obtained relationships between ln(γ/M) and
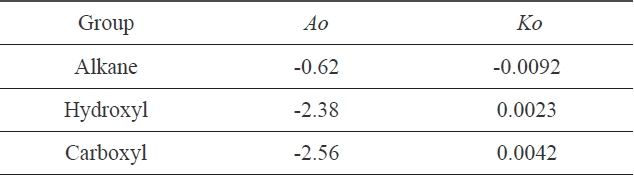
In Fig. 4, three different linear lines were obtained, showing theferent groups. Groups I, II, and III represented alkanes, carboxyl acids, and hydroxyl alcohols, respectively. The slope of group I is negative, while the slopes of group II and group III are positive. This indicates that the surface tension of alkanes decreased with the increase of the cohesive energy density due to the greater dispersion force, which means that the surface tension decreased with the increase of the non-polarity [1]. Similar results for the surface tension of alkanes were reported [7]. On the other hand, in carboxyl and hydroxyl groups, the surface tension increased with the increase of the cohesive energy density, which means that the surface tension can be increased with the decrease of the polarity. The constants in Eq. (13) were obtained from the slopes of the three groups; these values are arranged in Table 2.
According to Eq. (13), when ECED tends to zero,
, which means the greater A0, the greater the limit of γ/M ; in certain M conditions, the limit
is greater, that is, the smaller the polarity of the solvent, the greater the limit of the surface tension. In Eq. (13),
From these results, surface tension and cohesive energy density of coagulation bath solvents can be controlled by changing the mixing ratio of coagulation bath components. And, an effective
[Table 1.] Surface tensions and cohesive energy densities of some organic materials [6]
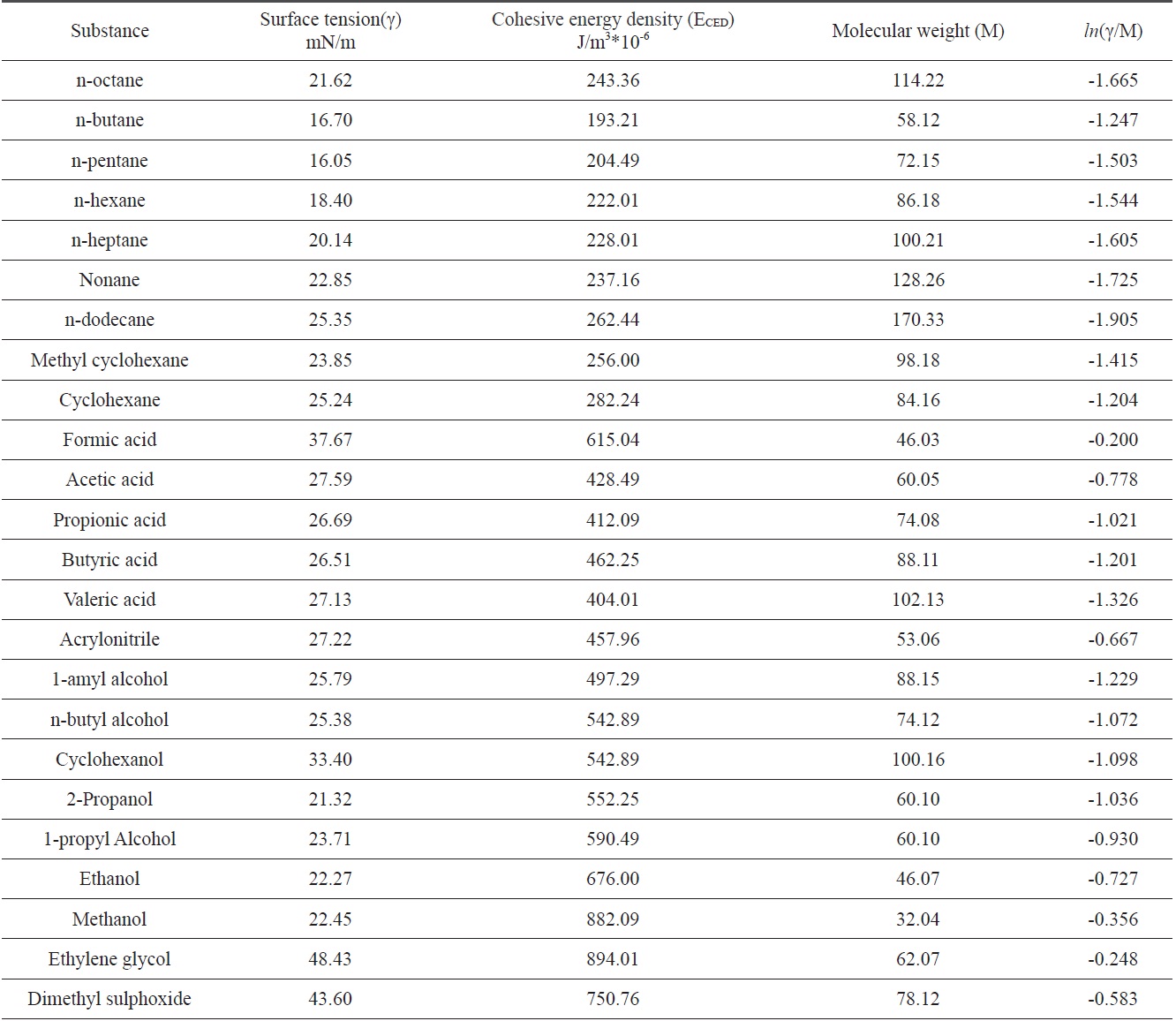
Surface tensions and cohesive energy densities of some organic materials [6]
[Table 2.] Constants of Eq. (13), obtained from Fig. 4
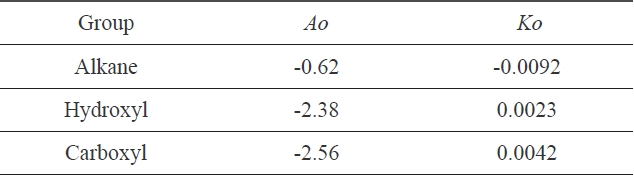
Constants of Eq. (13), obtained from Fig. 4
precipitation polymerization of the polyacrylonitrile (PAN) precursor can be obtained from a well controlled mixing ratio of coagulation bath solvents during the wet spinning of acrylonitrile.
A new coagulation model for monomers and the resultant equation are suggested; these relate to the surface tension and the cohesive energy density. We confirmed the correctness of the equation by applying some known organic solvents. With the model and the equation, the effective precipitation polymerization of a PAN precursor can be carried out by controlling the mixing ratio of coagulation for the bath solvent components in consideration of their surface tension, cohesive energy density, and polarity during the wet spinning of acrylonitrile.
![Surface tensions and cohesive energy densities of some organic materials [6]](http://oak.go.kr/repository/journal/11275/HGTSB6_2012_v13n3_182_T001.jpg)