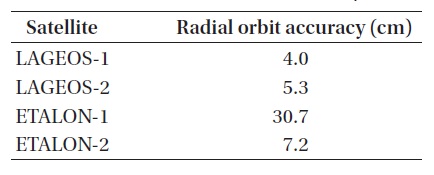
In this study, we present preliminary results of precise orbit determination (POD) using satellite laser ranging (SLR) observations for International Laser Ranging Service (ILRS) Associate Analysis Center (AAC). Using SLR normal point observations of LAGEOS-1, LAGEOS-2, ETALON-1, and ETALON-2, the NASA/GSFC GEODYN II software are utilized for POD. Weekly-based orbit determination strategy is applied to process SLR observations and the post-fit residuals check, and external orbit comparison are performed for orbit accuracy assessment. The root mean square (RMS) value of differences between observations and computations after final iteration of estimation process is used for post-fit residuals check. The result of ILRS consolidated prediction format (CPF) is used for external orbit comparison. Additionally, we performed the precision analysis of each ILRS station by post-fit residuals. The post-fit residuals results show that the precisions of the orbits of LAGEOS-1 and LAGEOS-2 are 0.9 and 1.3 cm, and those of ETALON-1 and ETALON-2 are 2.5 and 1.9 cm, respectively. The orbit assessment results by ILRS CPF show that the radial accuracies of LAGEOS-1 and LAGEOS-2 are 4.0 cm and 5.3 cm, and the radial accuracies of ETALON-1 and ETALON-2 are 30.7 cm and 7.2 cm. These results of station precision analysis confirm that the result of this study is reasonable to have implications as preliminary results for administrating ILRS AAC.
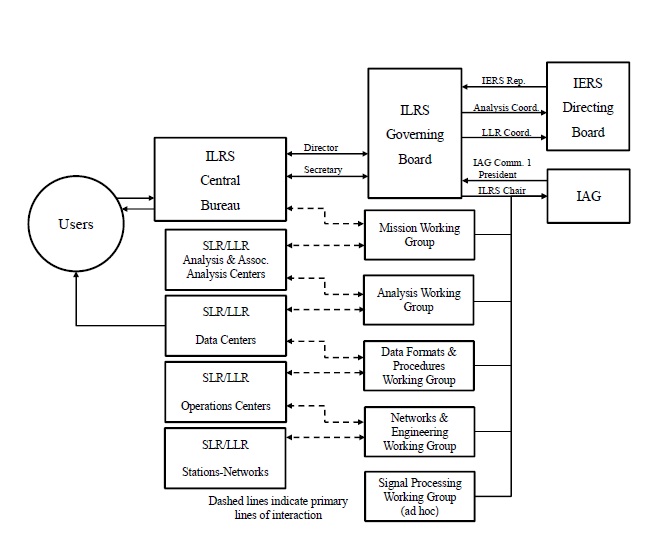
The International Laser Ranging Service (ILRS) is an international organization for overall management of operation and data processing of satellite laser ranging (SLR) and lunar laser ranging (LLR) systems (Pearlman et al. 2002). Established in 1998 by the International Association of Geodesy (IAG), the ILRS has been supporting research activities associated with provision and management of SLR/LLR observations, prediction and determination of satellite orbits, geodesy, geophysics, lunar research, etc. The ILRS also provides the International Earth Rotation Service (IERS) with essential data for the precise generation and maintenance of the international terrestrial reference frame (ITRF). Together with the International GNSS Service (IGS) and the International VLBI Service (IVS), the ILRS is one of the international organizations of the IAG that provide data of the Earth and its related measurements. Currently in March 2012, the ILRS is operating four operation centers (OCs), two global data centers (G-DCs), one regional data center (R-DC), 9 analysis centers (ACs), four lunar analysis centers (LACs), and 17 associate analysis centers (AACs). Also, the central bureau (CB) manages and controls the entire activity of the ILRS and the governing board (GB) sets general guidelines of the organization. Fig. 1 shows the whole organization chart of the ILRS.
The official, main products by the ILRS are largely classified into station coordinates and Earth orientation parameters (EOPs). Other products include analysis results of gravitational models of the Earth, precise orbit ephemerides (POEs) derived by precise orbit determination (POD) for satellites, models verifications related to satellite
dynamics, results from complementary POD for supporting other satellite missions, information of the lunar ephemeris and libration for studies on the inside of the Moon and the relativity theory (Pearlman et al. 2002). Among the organization components in the ILRS, the AC and AAC achieve scientific results by processing the SLR data and applying the consequences. By the SLR data processing, the AC creates the ILRS products of EOPs, the ILRS station coordinates, the precise orbits of LAGEOS, which is the representative, SLR-dedicated, geodetic satellite, and fundamental physical constants in geophysics. To achieve this, the SLR data processing and analysis of LAGEOS-1 and LAGEOS-2 must be included in the process and the EOPs including the station coordinate results and the ranges and time biases for individual stations should be generated weekly or sub-weekly. The AAC provides orbit predictions, time-related biases, and POEs, and station coordinates for satellites, and is encouraged to perform comparisons between the AC products and the combined solutions by other space geodetic techniques for the production of ITRF and the support for POD. Although the AC and the AAC produce similar outcomes with each other, the role of the AC is to derive them regularly at a stable level while the AAC creates parts of arbitrary products.
The most fundamental product for the operations of the AC and the AAC is the POD results of LAGEOS, but any precision standard for the POD results of LAGEOS is not specifically presented by the ILRS. Hence, an organization who is considering operating an AC or AAC can compare the POD results for LAGEOS between the current AC or AAC of the ILRS and other researches to determine whether the products are appropriate for the operation. The operation of an AC is practically significant in deriving such POD results stably and obtaining scientific attainments from them, while the operation of an AAC is important in deriving reliable POD results which serve as a basis for the AC products and scientific attainments. A country operating an AC of the ILRS is regarded as verified that their technology for system operation and data processing of SLR has reached a level of meeting the international requirements, and an operation of an AAC means that they hold the technology of SLR data processing for reliable products and are ready to apply that technology. The most important meaning of hosting and operating an AC or AAC of the ILRS is that they can internationally lead the researches on the data processing and application of SLR. Currently in Asia, China, Japan, and Australia have joined the ILRS as active members and are operating ACs and AACs. In Korea, the recent development of the accurate ranging system for geodetic observation-mobile (ARGO-M), a mobile SLR system, by the Korea Astronomy and Space Science Institute (KASI) is stimulating the demand of data processing and application of SLR, and it has become required to acquire the technology of SLR data processing at a level of the ILRS AAC for reliable system verifications and scientific results (Jo et al. 2011).
SLR is known to be the most precise method for measuring the distance between a satellite and a ground station (Seeber 2003). The precision of a single shot is about 5-50 mm and that of normal point (NP) data, for which the measured values are averaged within the data range of about two minutes to prevent a scattering of the observing data, is as high as 1-12 mm (Montenbruck & Gill 2000). The most representative products using SLR data are the satellite POD and the POE from it. Recently, as the precision of SLR observations is improving, SLR is increasingly more applied as a tool for verifications of POD results or independent calibrations of observations from other tracking systems such as the global positioning system (GPS), rather than for researches of performing POD only with SLR observations (Zhu et al. 1997, Barlier et al. 2001, Schumacher et al. 2001, Urschl et al. 2005, 2007, Kim et al. 2009, Hwang et al. 2011). However, the high precision of distance measurement of SLR data is a merit also for POD, and SLR data are still used frequently for orbit determinations for the SLR-dedicated geodetic satellites. Particularly, in the cases of LAGEOS-1 and LAGEOS-2, which are constantly observed by various countries, the post-fit residuals obtained at the final stage after a converging process of estimation after the POD using SLR observations are used as a measure to check the state of a ground station and to determine whether the capability of operating a ground station meets the ILRS standards. Therefore, it should be most urgent for securing the data processing technology at a level of the ILRS AAC to acquire reliable results through the POD of SLR-dedicated geodetic satellites such as LAGEOS-1 and LAGEOS-2.
In this study, as a preliminary research for an operation of an ILRS AAC, we performed POD followed by analysis and orbit quality assessment of the generated POE results for LAGEOS-1, LAGEOS-2, ETALON-1, and ETALON-2, the representative SLR-dedicated geodetic satellites, using GEODYN II by NASA/GSFC, the representative program for POD and parameter estimation. NP data, which currently is the primary releasing form of ILRS data, are used for the SLR observations. To verify the POD results, we first analyze the post-fit residuals which are most widely used in confirming performances of orbit determination of SLR-dedicated geodetic satellites. Additionally, an external orbit comparison is performed to verify the reliability by a comparison with orbit determination results by another independent organization, where we use the consolidated prediction format (CPF) provided by the Predictions Formats Study Group at the ILRS for the external orbit (http://ilrs.gsfc.nasa.gov/products_formats_procedures/predictions/cpf.html). Finally, we perform a station precision analysis to confirm the results of ILRS station precision.
2. PRECISE ORBIT DETERMINATION
2.1 Satellites for Geodetic Missions
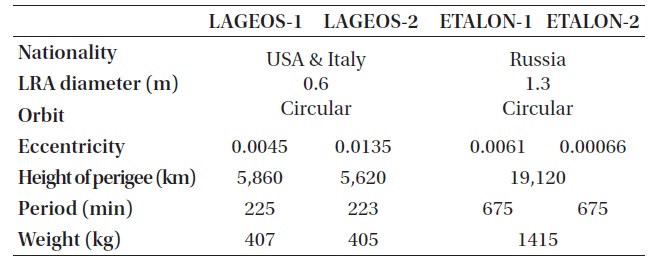
Currently in March 2012, 37 SLR satellites in total are carrying out their missions related to space geodesy except for the LLR-related satellites (http://ilrs.gsfc.nasa.gov/satellite_missions/list_of_satellites/). Such SLR satellites are playing important roles in obtaining results from the studies on Earth tide, oceans, the atmosphere system, and their interactions with each other. Particularly, as the precision of SLR observations and PODs using them improves, by data processing of LAGEOS-1 and LAGEOS-2, which are the representative, SLR-dedicated, geodetic satellites, the post-fit residuals are as small as 1 cm. LAGEOS-1, LAGEOS-2, ETALON-1, and ETALON-2 are the most representative SLR-dedicated geodetic satellites of which data are processed at the AC and AAC of the ILRS and information is presented in Table 1. The actual appearances of the satellites are shown in Fig. 2 (http://ilrs.gsfc.nasa.gov/satellite_missions/list_of_satellites/). As seen in Fig. 2, the shapes of LAGEOS-1, LAGEOS-2, ETALON-1, and ETALON-2 are spherical, of which the advantage is the minimal effect by a perturbation such as solar radiation pressure. Also, most SLR-dedicated geodetic
[Table 1.] Satellites of geodetic missions (http://ilrs.gsfc.nasa.gov/satellite_missions).
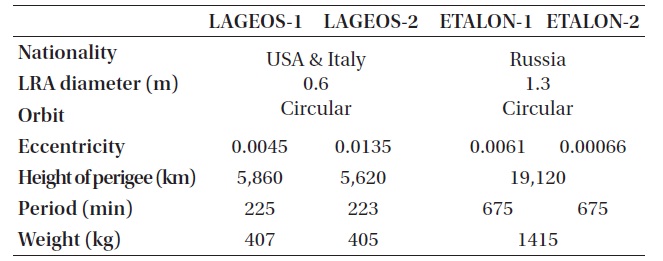
Satellites of geodetic missions (http://ilrs.gsfc.nasa.gov/satellite_missions).
satellites suffer not much from air drag since they are in the medium earth orbit or higher orbits. Thus, these spherical types of SLR-dedicated geodetic satellites can be used as the best tools for confirming the level of a dynamic model.
In general, POD of a satellite means to determine the state vector of the satellite at a given time precisely by using the measurements and an estimation theory and obtain a POE with a cm-level precision for positioning. The state vector are expressed by the position and velocity of the satellite, the solar radiation pressure constant (CR) and the air drag constant (CD) in the dynamic model, empirical acceleration-related constants, the position of the ground station in the measurement model, the zenith delay of the atmospheric model, and a range bias. A wide range of satellite-tracking data from GNSS, SLR, DORIS, radio, and optical observations are used for the measurements. The batch estimation of Least-Square Batch Filter and the sequential estimation of extended Kalman filter are popular estimation methods for orbit determination, where the least-square batch filter is most widely used for POD. More recently, also a batch filter using the unscented transformation (UT), which is robust against a nonlinearity, has been studied (Park et al. 2010, Kim et al. 2011).
For POD, a dynamic model is required to set the equation of motion considering various perturbations on the satellite, and predict the next state vector by integrating the state vector numerically with time. The dynamic model is largely divided into gravitational perturbations and non-gravitational perturbations, and is expressed by Eqs. (1) and (2).
Here,
and
denote the position and velocity vectors of the satellite, respectively,
the perturbation expressed in acceleration. Typical examples of this perturbation include an effect by the asymmetric field of the Earth's gravity, gravitational effects by the Sun, the Moon, and the planets in the solar system, the solar radiation pressure, the Earth albedo, air drag, the general relativity, the polar motion of the Earth, and the Earth and ocean tides.
In the next step, a measurement model is required to be built to acquire tracking data of the satellite and generate observations. The principle of distance measurement using a SLR system is simple. The distance between the ground station and the satellite is calculated by measuring the round trip time of laser from the ground station to the laser retro-reflector array (LRA) on the satellite. Errors from various sources are involved in this measurement, but most SLR systems have an advantage of relatively simple modeling of observation since a delay error by the ionosphere, which is inverse proportional to frequency squared, can be ignored by using a Nd:YAG laser at the optical wavelength of 532 nm for the observation. On the other hand, it is important to calculate the error from the tropospheric refraction precisely owing to the significant influence by the weather condition in the atmosphere. The distance measured by a SLR system between the reference point of laser transmission/reception at the ground station and the laser reflector on the satellite can be expressed by Eq. (3) (Tapley et al. 1985).
Here,
In this study, we use SLR NP data for the observational data for the POD of LAGEOS-1, LAGEOS-2, ETALON-1, and ETALON-2, of which the NP data are provided by the two G-DC of the ILRS through their homepage or anonymous FTP (http://ilrs.gsfc.nasa.gov/products_formats_procedures/ftp_archives/index.html). Here, we obtaine the NP data through the ftp server (ftp://cddis.gsfc.nasa.gov/pub/slr/data/npt/) provided by the Crustal Dynamics Data Information System (CDDIS) at the NASA.
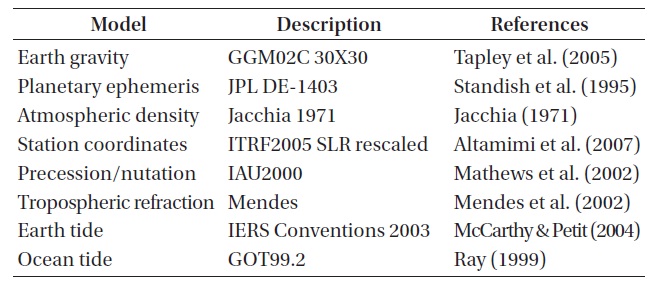
[Table 2.] Dynamic and measurement models for POD.
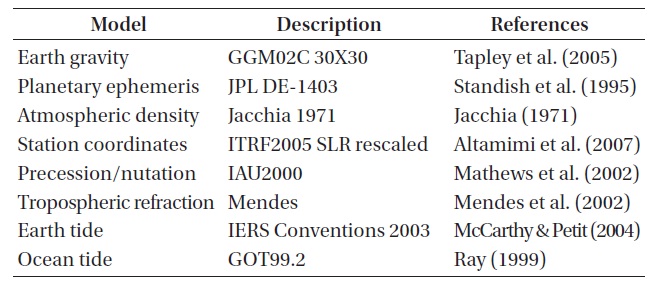
Dynamic and measurement models for POD.
Data for one week from June 2 to June 8, 2008 are used, and the state vector result from the previous orbit determination is used for the prior value for each satellite in the POD. The required information for the orbit determination of each satellite is presented in Table 1, which is available from the information provided by the ILRS. For the POD, we adopt a weekly-based processing of SLR observations using GEODYN II which is one of the software tools used at the AC or AAC.
Table 2 summarizes the modeling information of GEODYN II for the POD. We use the grace gravity model (GGM02C) by Tapley et al. (2005) for the Earth gravity model. Because of the relatively higher altitude of the measured satellites compared to general LEO satellites, dimensions of the gravity field are limited to 30 × 30 which are consistent with the current dimension limit at the ILRS AAC for efficient PODs considering altitudes. For the planetary ephemeris for the gravity of the Sun, the Moon, or the planets in the solar system, we use DE-1403 which uses the derivatives from the Jet Propulsion Laboratory (JPL) DE-403 (Standish et al. 1995). The Jacchia model (Jacchia 1971) is used for the atmospheric density model, the ITRF2005 SLR rescaled (Altamimi et al. 2007) for the station coordinates, and the IAU2000 model (Mathews et al. 2002) for the precession and nutation related values. We use the model by Mendes et al. (2002) for the tropospheric delay, and the models of IERS Conventions 2003 (McCarthy & Petit 2004) and GOT99.2 (Ray 1999) for the Earth and ocean tides, respectively. A least-square batch filter is applied as the estimation theory to estimate the parameters including the position and velocity of the satellite, the position and velocity of the ground station, the solar radiation pressure constant (CR), a constant related to an empirical general acceleration, and the range bias. The air drag constant (CD), which is often one of the parameters to be estimated in a general POD process, is not included in this study as in the cases at other ACs or AACs since the effect by the atmospheric density is ignorable for the SLR-dedicated geodetic satellites at such high altitudes as LAGEOS or ETALON. On the other hand, while at some ACs or AACs, the solar radiation pressure constant (CR) may be excluded from their estimations or set the range bias zero in their PODs, we estimate as many major parameters as possible for results in more general situations.
In general, verification methods for the results from orbit determination are largely classified into three categories. The first one is the analysis of post-fit residuals, in which the precision is verified by the residual values of orbit determination obtained finally after the iteration of the POD estimation, the second one is the overlap comparison, which checks how the results are self-consistent by overlapping the starting and ending points of a continuous range of orbit determination, and the final one is the external orbit comparison where the POD results are compared with those from other models or softwares. In the cases of SLR-dedicated geodetic satellites, the precision is mostly verified by the post-fit residuals which corresponds to the precision in the direction of the distance since the precision in the radial direction is high because of the precise measurement of distance while the precisions in the along and cross-track directions are low. Particularly, for the SLR-reference satellites with a geometric appearance of sphere such as LAGEOS and ETALON, the residual of orbit determination itself has the highest priority as a standard in the determination of the precision of orbit determination. If a POE is available for a comparison, it can be indirectly checked through the external orbit comparison in what error range the currently generated orbit is consistent with another orbit. A disadvantage in the case of a SLR-dedicated geodetic satellite is that the verification is confined in the precision range of the compared orbit itself because of the small number of POEs available for the comparison. Also, in the case of SLR-dedicated geodetic satellites, each station performs analysis of precision for NP data and their results can be used as another indirect verification for the precision of POD results. In this study, we verify the precision of the obtained orbits by the analysis of post-fit residuals, the external orbit comparison, and the station precision analysis.
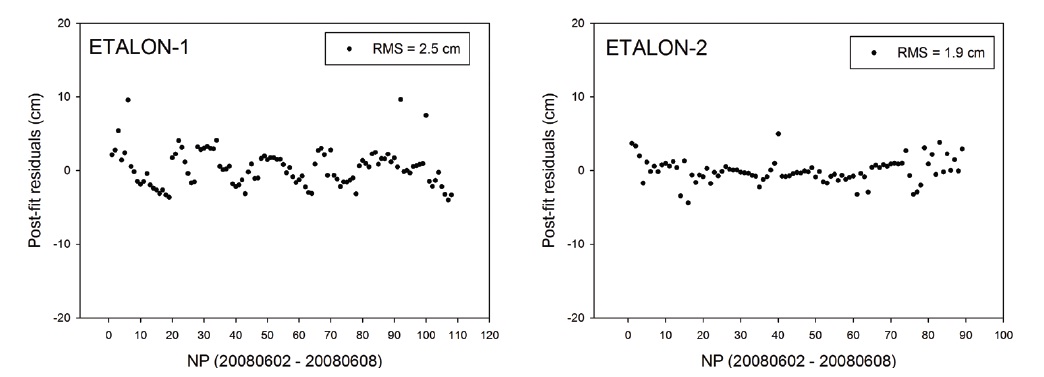
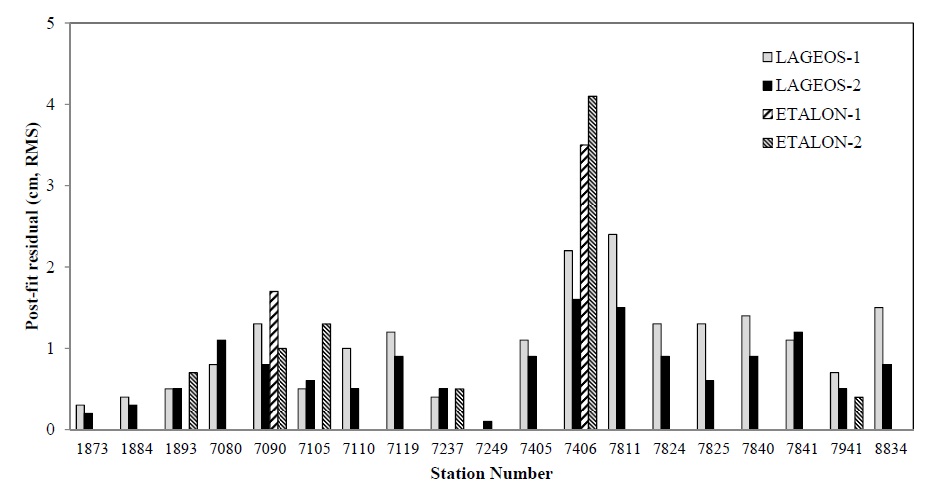
We check first the post-fit residuals for the verification of the POD results. In the estimation process of orbit determination, the O-C residual between the measured distance of the satellite (O) and the computed distance (C) is obtained at each iteration step. The post-fit residual is the
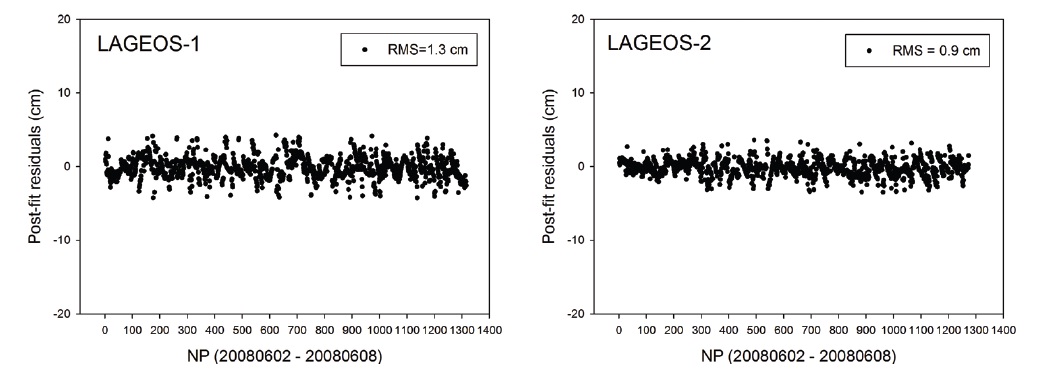
[Table 3.] The result of post-fit residuals.
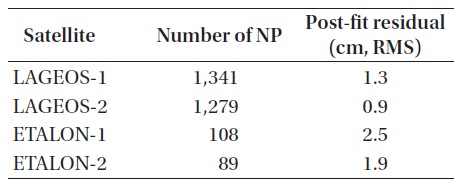
The result of post-fit residuals.
final O-C residual after the orbit determination is completed by meeting the converging condition for the estimation. Therefore, confirming this post-fit residual is one of the direct methods for verifying the precision of determined orbits. Particularly, this method is applied as the primary verification of the orbit determination results for the SLR-reference satellites since the precision of the NP data is very high in the cases of those satellites. Fig. 3 shows the post-fit residuals for LAGEOS-1 and LAGEOS-2, and Fig. 4 shows those for ETALON-1 and ETALON-2. In Table 3, the post-fit residuals of each satellite are presented in root mean square (RMS). We can see that the residuals are 1.0?2.0 cm RMS for LAGEOS-1 and LAGEOS-2 and 2.0?3.0 cm RMS for ETALON-1 and ETALON-2. In general, the post-fit residuals after an orbit determination for LAGEOS-1 and LAGEOS-2 are known to be 1.0?2.0 cm, while those values obtained by Zhao et al. (2008) from PODs at a 3-day interval for the SLR NP data of LAGEOS-1 and LAGEOS-2 from 2005 to 2008 were about 1.2 cm RMS in average for both LAGEOS-1 and LAGEOS-2. In the study by Otsubo (2000), the post-fit residuals were obtained to be 1.5?2.0 cm RMS for 7-day data of the LAGEOS satellites and 1.5?4.0 cm RMS for 14-day data of the ETALON satellites. Noomen (2001) showed that the post-fit residuals obtained by the previous studies were 1.0?3.0 cm for LAGEOS-1 and LAGEOS-2. The Natural Environment Research Council (NERC) Automatic Global SLR Normal Point Quality Analysis in U.K., one of the ILRS ACs, reported post-fit residuals of about 2.0 cm RMS based on their 6-7-day data of 10 stations (http://sgf.rgo.ac.uk/slrweb/auto_analysis.html). Comparing with those results, we can see that the post-fit residuals from our POD have a consistent precision with those from the previous studies and from the ILRS AC. This implies that this study of using GEODYN II for SLR data processing and POD can obtain the results at a level of an ILRS AAC.
3.2 External Orbit Comparison (CPF)
In the cases of LEO satellites or GPS satellites where a number of POEs are available from orbit determinations by various organizations, the method of external orbit comparison, in which the confidentiality is secured by comparing individual precise orbits, is mainly used for the verification of orbit precision. On the other hand, in the cases of SLR-dedicated geodetic satellites at high altitudes like LAGEOS and ETALON, the post-fit residuals are mainly used for the precision verification rather than the external orbit comparison since precise orbits for the comparison of precision are not released so often and the precision of the SLR distance measurement itself is too high. Only in the cases of SLR-dedicated geodetic satellites, the ILRS provides CPF of which the positional precision is known to be from a few to a few tens meters (http://ilrs.gsfc.nasa.gov/products_formats_procedures/predictions/cpf.html). A disadvantage of CPF is that the precision can be verified only within a range of general orbit precision of CPF since this is not a POE and the orbit precision is not clearly presented in many cases depending on the time periods. To generate CPF as a product of an ILRS AAC in the future,
however, we try to convert the results of orbit determination to the form of CPF and use them for the external orbit comparison to compare the orbit precisions. We assume that the orbit precision of CPF stays within the general precision range of CPF (from a few to a few tens meters) for the comparison in the radial direction since the CPF over the period of our study does not include any information on the orbit precision either. This means that the comparison results are not for an absolute orbit precision but for a relative precision compared to the CPF. This may rather be a method of confirming the relative precision of the used CPF, by putting together the results of the post-fit residuals and the external orbit comparisons with CPF.
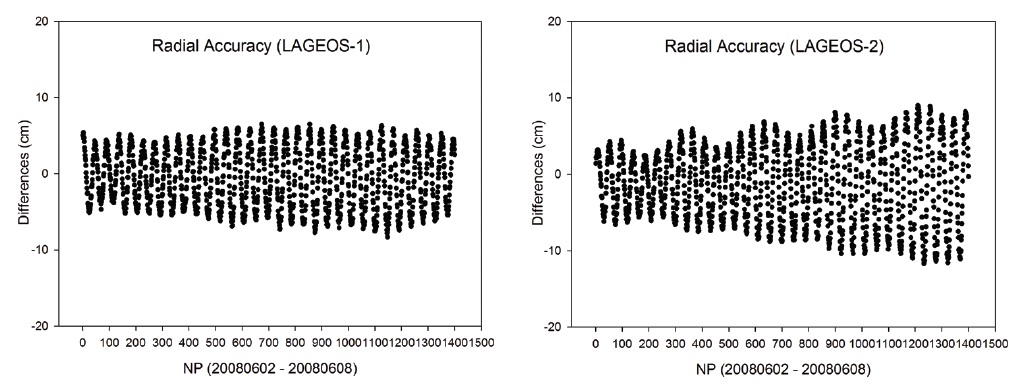
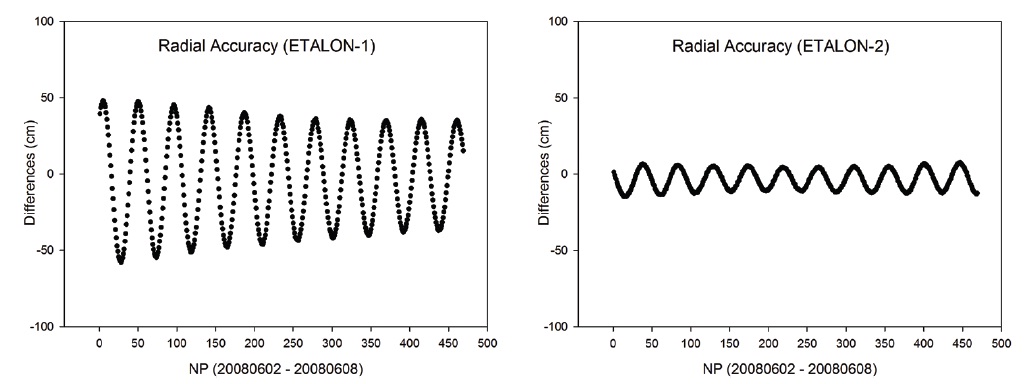
Figs. 5 and 6 show the comparison results for the component of radial direction between the CPF of each satellite and the results from this study, and Table 4 summarizes the precision in the radial direction in RMS. As a result, in the radial direction, we obtain the precision of 4?5 cm for LAGEOS-1 and LAGEOS-2, and 7?30 cm for ETALON-1 and ETALON-2. Considering that the resulting precision is at a level of a few to a few tens centimeters in the radial direction, we can see that our results are different
[Table 4.] The result of external orbit comparison.
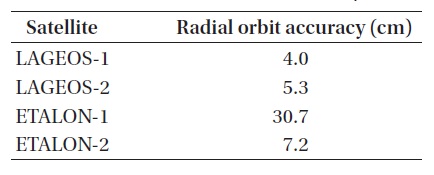
The result of external orbit comparison.
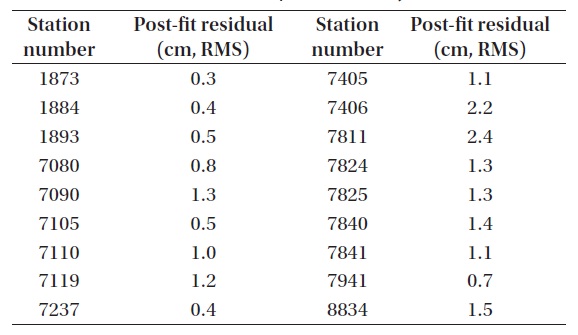
[Table 5.] The result of station precision analysis (LAGEOS-1).
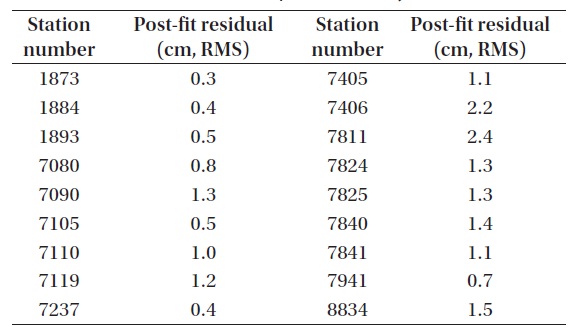
The result of station precision analysis (LAGEOS-1).
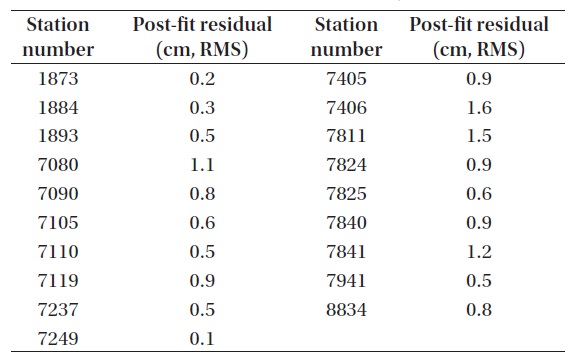
[Table 6.] The result of station precision analysis (LAGEOS-2).
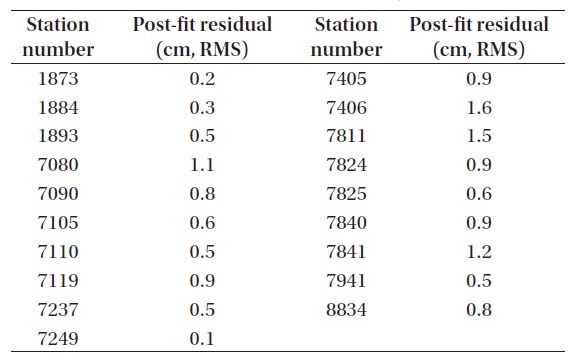
The result of station precision analysis (LAGEOS-2).
from CPF by a few to a few tens centimeters in the radial direction. This result is within the general error range of the CPF precision, and it is indirectly confirmed that CPF contains relative errors of a few to a few tens centimeters in the radial direction compared to our results.
3.3 ILRS Station Precision Analysis
We perform an assessment of the ILRS station precisions using the post-fit residuals for an analysis and indirect comparison of the POD results. For this purpose, we first derive RMS values of the post-fit residuals obtained from the PODs of LAGEOS-1, LAGEOS-2, ETALON-1, and ETALON-2 for each ILRS station, and then apply those values to derive and analyze the precision for each station.
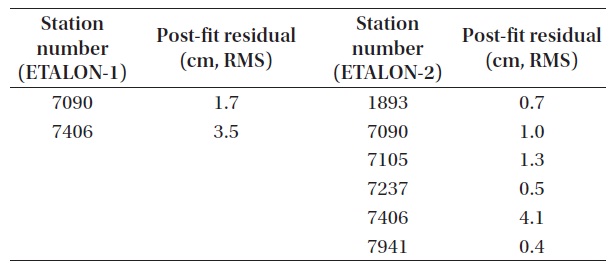
[Table 7.] The result of station precision analysis (ETALON-1, ETALON-2).
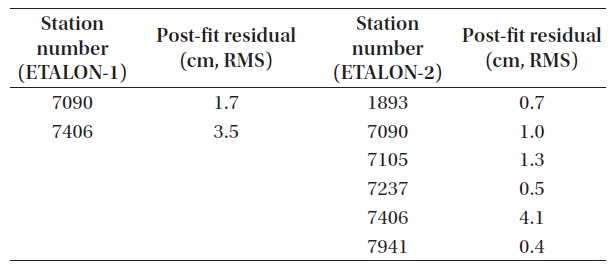
The result of station precision analysis (ETALON-1, ETALON-2).
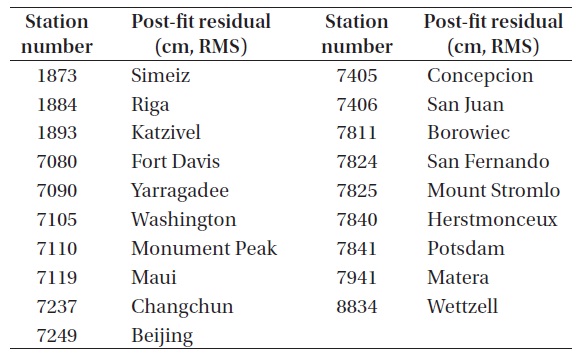
[Table 8.] The information of ILRS stations.
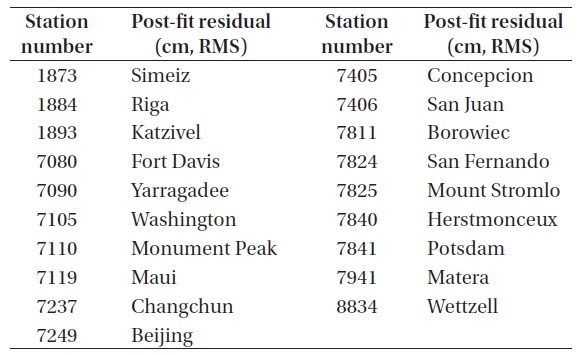
The information of ILRS stations.
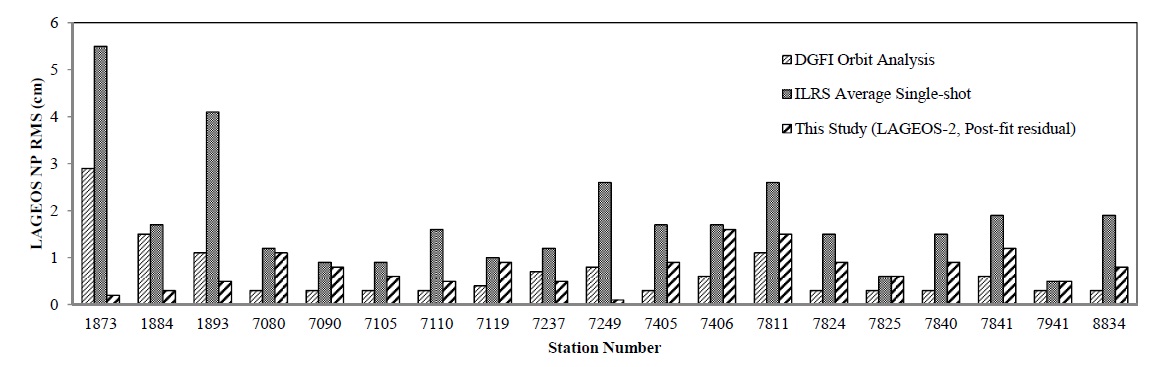
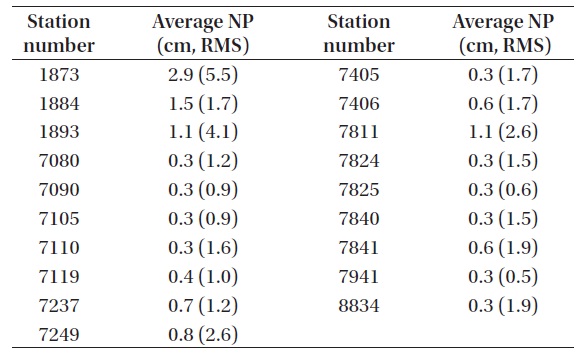
The ILRS provides the SLR global performance report quarterly based on the rapid orbital analysis or quick look analysis by ACs (http://ilrs.gsfc.nasa.gov/stations/site_info/global_report_cards/perf_2011q4_wLLR.html). The SLR global performance report cannot directly be compared to the post-fit residuals from a POD since this report contains mainly the precision of the NP data itself, the range bias for the distance measurements, and statistical information related to them, for the SLR-dedicated geodetic satellites. However, this report can be used to confirm indirectly the performance of the current POD results by comparing the precisions of the NP data itself and the POD results. The AC/AAC report section in the ILRS report introduces from time to time the post-fit residual results after PODs by ACs or AACs for SLR-dedicated geodetic satellites, but we exclude this report from the comparison since its data are neither plenty enough nor organized as a whole, and instead we adopt the AC results of orbit analysis and the mean NP precision in RMS of the LAGEOS satellite presented in the SLR global performance report. The AC results of orbit analysis and the mean NP precision in RMS of the LAGEOS are derived together at the same time for the entire data of a quarter and do not represent the weekly precision used in this study, which can still be predicted indirectly through the precision of the entire quarter. Here, we compare the precision indirectly with the assessment result of each ILRS station precision using the SLR global performance report in the corresponding quarter to the period of this study.
Tables 5-7 shows the results of station precision. Brief information for each station is presented in Table 8. The results for all the satellites are summarized in Fig. 7. The results of individual stations show that the station precision is similar with each other in post-fit residual in the cases of LAGEOS-1 and LAGEOS-2. It is confirmed that the precision of LAGEOS-2 is higher than that of LAGEOS-1 in general. The precisions of most stations are around 1 cm RMS while the RMS values of a few stations (7406, 7811) are rather large to decrease the precision of the POD results from all the LAGEOS satellites. Also in the cases of ETALON-1 and ETALON-2, the post-fit residuals show similar precisions between different stations, but this is not clearly confirmed due to the small number of stations used. However, it is confirmed that the POD precision of all the satellites can be degraded when there are stations with poor RMS values as in the cases of the LAGEOS satellites.
[Table 9.] The result of SLR global performance report (LAGEOS).
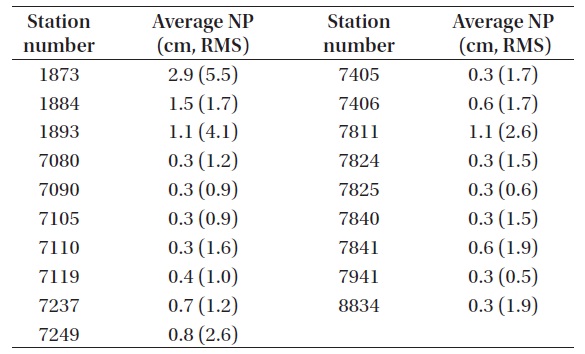
The result of SLR global performance report (LAGEOS).
The results of the ILRS SLR global performance report in the quarter including the same period are summarized in Table 9. The foremost values are the AC results of orbit analysis in RMS and the values in parentheses are the mean NP values of single observations by the LAGEOS satellites in RMS. The results from the Deutsches Geodaetisches Forschungsinstitut (DGFI) among the ACs are used for the results of orbit determination. The DGFI results are from the weekly processing of SLR observations using the DGFI Orbit and geodetic parameter estimation software. Fig. 8 compares the post-fit residuals from our POD for LAGEOS-2, the DGFI results of orbit analysis, and the mean LAGEOS NP precision from the ILRS in RMS. From this comparison, we can confirm in most cases that our post-fit residuals are better than the DGFI results of orbit analysis or the mean LAGEOS NP precision of the ILRS, and that we obtain precise orbits from our POD.
In this study, we performed a POD using SLR observations and a verification of the resulting precision for LAGEOS-1, LAGEOS-2, ETALON-1, and ETALON-2, the representative SLR-dedicated geodetic satellites, as a preliminary study to prepare for an ILRS AAC. As a result of the verification of post-fit residuals, we obtained the precisions at levels of an ILRS AC with 1?2 cm RMS for LAGEOS-1 and LAGEOS-2 and 2?3 cm RMS for ETALON-1 and ETALON-2. From the comparison with the ILRS CPF using the method of external orbit comparison, it was confirmed that the differences in the radial direction are 4?5 cm RMS for LAGEOS-1 and LAGEOS-2 and 7?30 cm RMS for ETALON-1 and ETALON-2. Through the analysis of station precision we found that the stations with high precisions and those with poor precisions can be distinguished to be reflected to a POD strategy, and that the precision of our results are similar to or better than those of the orbit analysis by an ILRS AC or the ILRS NP precision in RMS. One of the most important roles of the ILRS AACs is to perform PODs and derive reliable products for geodetic satellites, particularly for the LAGEOS satellites. In conclusion, our results from the SLR data processing and POD using GEODYN II are meaningful in a preliminary stage to reach the level of an ILRS AAC in the performance and results of SLR data processing.