In global and competitive market, the need for establishing a longer-term relationship that fosters cooperation among suppliers and their customers has been highlighted. However, many purchasers find it difficult to determine which suppliers should be targeted as each of them has varying strengths and weaknesses in performance. Moreover, the importance of each criterion tends to vary from one purchaser to others. This problem becomes more complicated as the simultaneous evaluation is required in terms of qualitative and quantitative criteria. So, every decision needs to be integrated by trading off performances of different suppliers at each supply chain stage.
One of the main characteristic of supplier selection is that this task is characterized by an imprecision and incomplete of data which results in vagueness of information related to decision criteria. Stochastic models are usually based on representation of existing uncertainty by probability concepts and are, consequently, limited to tackling the uncertainties captured (Aliev
Li
A number of studies have been devoted to examining supplier selection methods. Quantitative techniques have become increasingly applied recently. A comprehensive review of numerous quantitative techniques used for supplier selection has been done by Weber
Some researches used single objective, such as cost, to evaluate suppliers. Kaslingam and Lee (1996) developed an integer programming model to select suppliers and to determine order quantities with the objective of minimizing total supplying costs which include purchasing and transportation costs. Caudhry
As an extension of single objective techniques, multi- objective mathematical programming has been proposed to solve a more complex supplier selection problem. Weber
This paper focuses on fuzzy multi-objective linear programming (fuzzy MOLP) to deal with supplier selection problem. Kumar
Although there were a number of publications adopting fuzzy programming model in supplier selection problem in the literature, most of them rely on the application of the existing method and very few researches have concerned with the improvement in the methodological process of deriving optimal solution. Kagnicioglu (2006) proposed super-transitive approximation to determine the weights of objectives and constraint in formulating fuzzy MOLP model in supplier selection and solved the model using max-min operator and weighted additive model. Yucel and Guneri (2010) proposed a new method of weights calculation in fuzzy MOLP supplier selection. Both researches mentioned above only focus on the process for weights calculation for fuzzy objective and constraints.
It has been approved that solving fuzzy MOLP using max-min operator may not result in a optimal solution (Tseng and Chen, 1998; Dubois and Fortemps, 1999; Lin, 2004). Such a lack has been resolved by Li
Ghodsypour and O’Brien, 1998). Purchasing risk is included as one objective to measure the risk of potential loss incurred if purchaser allocates a certain amount of product to purchase to a certain supplier. To this end, Taguchi loss function (TLF) is used to quantify this risk. AHP is employed to determine relative important between fuzzy goals and constraints.
The rest of the paper is organized as follows. The comprehensive description of the proposed model is described in section 3. It includes the theoretic descriptions for Taguchi Loss Function, AHP, Fuzzy Multiobjective Linear Programming, the proposed “an enhanced two-phase approach” to solve fuzzy MOLP. This section is closed with the “solution prodedures” which describes step by step procedures to solve fuzzy MOLP supplier selection problem. Then a numerical experiment is presented in Section 4. Finally, the paper is concluded in section 5.
3. THE PROPOSED INTEGERATED METHOD
This section presents all methods involved in our fuzzy MOLP model. First, Taguchi loss function is described to quantify the risk associated with purchasing decision, followed by AHP to calculate a relative importance of sub-criteria used to measure risk as well as the relative importance between objectives and constraints in the final formulation. Next, fuzzy MOLP supplier selection model and an enhanced two-phase approach are presented.
In traditional system, the product is accepted if the quality measurement falls within the specification limit. Otherwise, the product is rejected. The quality losses occur only when the product deviates beyond the specification limits, therefore becoming unacceptable (Pi and Low, 2005). Taguchi suggests a narrower view of quality acceptability by indicating that any deviation from quality’s target value results in a loss. If the quality measurement is the same as the target value, the loss is zero. Otherwise, the loss can be measured using a quadratic function (Kathley and Waler, 2002).
There are three types of Taguchi loss functions: “target is best” (two-sided
3.2 Analytical Hierarchy Process
The analytic hierarchy process (AHP) was developed to provide a simple but theoretically multiplecriteria methodology for evaluating alternatives (Saaty, 1980). The major reasons for applying AHP are because it can handle both qualitative and quantitative criteria and because it can be easily understood and applied by the DMs. AHP involves the principles of decomposition, pair-wise comparisons, and priority vector generation and synthesis.
The procedures of AHP to solve a complex problem involve six essential steps (Lee, 1999): define the unstructured problem and state clearly the objectives and outcomes; decompose the problem into a hierarchical structure with decision elements (e.g., criteria and alternatives); employ pair-wise comparisons among decision elements and form comparison matrices; use the eigen value method to estimate the relative weights of the decision elements; check the consistency property of matrices to ensure that the judgments of decision makers are consistent; and aggregate the relative weights of decision elements to obtain an overall rating for the alternatives.
3.3 Fuzzy Multi-objective Linear Programming
A linear multi-objective problem can be stated as: find vector
subject to:
where
Zimmermann (1978) first adopted fuzzy programming model proposed by Bellman and Zadeh (1970) into conventional LP problems. The fuzzy formulation for eq. (5)-(7) can be stated as
subject to:
The above fuzzy MOLP is characterized by linear membership function whose value changes between 0 and 1. The membership function (
and linear membership function for fuzzy constraints is given as
Zimmermann (1978) proposed a max-min operator approach to solve the above fuzzy MOLP. The Eq. (5)~(7) can be transformed into the following crisp formulation by introducing additional variable
3.4 Enhanced two-Phase Fuzzy Programming
Li
Step 1: Solve the max-min operator problem and output the optimal value, say
Step 2: Set the lower bound
for objective function and
for fuzzy constraints and solve the following model to get a final solution
It should be noted that the value of minimum acceptable achievement level is a compromise preference value of decision maker. However, this method may not necessarily yield a feasible solution when the minimum acceptable achievement level is closer or equal to the most optimistic value. Moreover, due to the problem structure of supplier selection under consideration, formulating linear programming requires a careful parameter setting because selection criteria are quantified using wide range of numerical input. Inappropriate parameter setting may also result in infeasible solution. To release the above-mentioned shortcomings and to help obtain a more reasonable compromise solution, therefore, this research proposes an enhanced two-phase approach of fuzzy MOLP. Namely, we propose to solve the following model to get the final solution
where
3.5 Supplier Selection Problem
In this section, we formulate a mathematical model of fuzzy MOLP supplier selection. The following notations are defined in order to describe the model.
i = index for supplier (i = 1, 2, …, N)
D = demand of buyer (unit)
B = total budget of buyer to purchase product ($)
xi = order quantity to supplier i (unit)
pi = unit price of supplier i ($)
fi = service level of supplier i (% fulfillment)
ri = purchasing risks of supplier i (% risk)
Ci = capacity of supplier i (unit)
The MOLP model for supplier selection is as follow:
subject to:
Eq. (19) minimizes the net cost for ordering product to satisfy demand. Eq. (20) maximizes the service level of suppliers. Eq. (21) minimizes the purchasing risk when the firm allocates a certain amount of product to purchase to a certain supplier. Eq. (22) puts restriction that order quantity assigned to suppliers must satisfy the total demand. Eq. (23) ensures that the total cost of purchasing does not exceed the amount of budget allocated by the firm. Eq. (24) guarantees that the order quantity assigned to each supplier will not exceed supplier capacity limit. Eq. (25) is non-negativity constraint.
The proposed fuzzy MOLP supplier selection problem is constructed through the following steps:
Step 1: Define the criteria for supplier selection problem
Step 2: Construct the MOLP supplier selection problem according to defined criteria (minimize purchasing cost, maximize service level, and minimize purchasing risk) and constraint of the buyer and suppliers. The purchasing risk is quantified as followed:
a. Define sub-criteria
b. Measure the relative important of sub-criteria using AHP
c. For each sub-criteria, define a target value, calculate loss coefficient and Taguchi loss
d. Find weighted Taguchi loss by employing the output of AHP. This value is used in MOLP model as the coefficient of objective of minimizing purchasing risk
Step 3: Find membership function for each criteria and constraint.
a. Determine a lower bound of each objective by solving MOLP as a single objective supplier selection problem using each time only one objective.
b. As in a), determine an upper bound of each objective by solving MOLP as a single objective supplier selection problem using each time only one objective.
Step 4: Calculate relative importance of criteria and constraints using AHP.
Step 5: Reformulate the MOLP supplier selection into equivalent crisp model using the enhanced two-phase fuzzy MOLP and find the set of feasible solution.
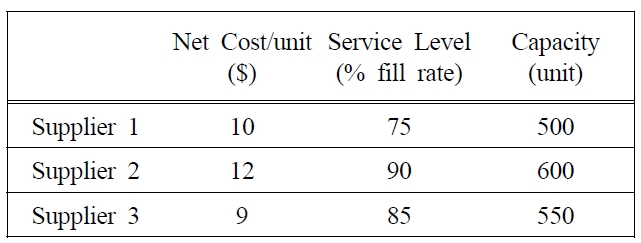
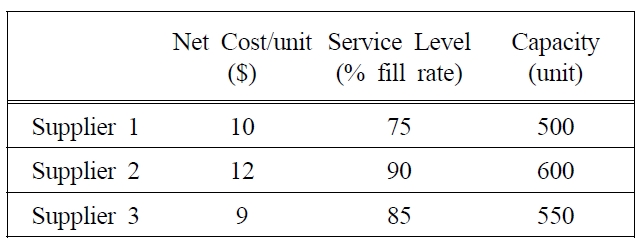
Suppose that one firm should manage three suppliers for one product. Management wants to improve the efficiency of the purchasing process by evaluating their suppliers. The management considers three objective functions i.e. minimizing net cost, maximizing service level and minimizing purchasing risk subject to constraint regarding demand of product, supplier capacity limitation, firm’s budget allocation, etc. The estimated value of suppliers’ net price, service level and suppliers’ capacity are given in Table 1. An allocated budget of the firm to purchase the product is $20,000. The demand is a fuzzy number and is predicted to be about 1400 unit with refraction of-100 and 150 unit.
[Table 1.] Suppliers’ Quantitative Information.
Suppliers’ Quantitative Information.
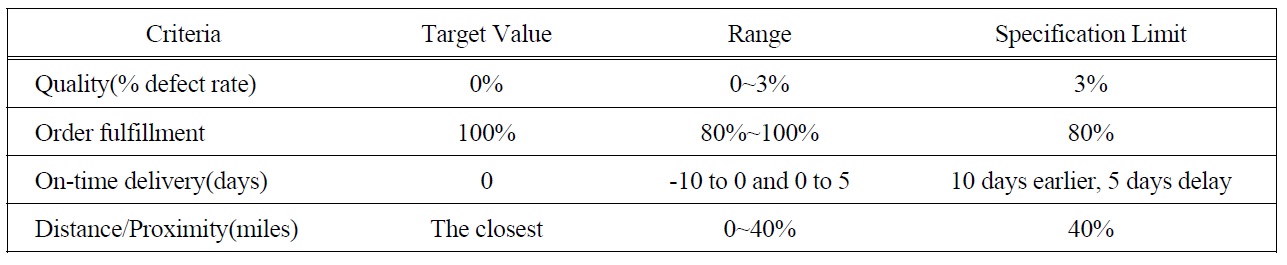
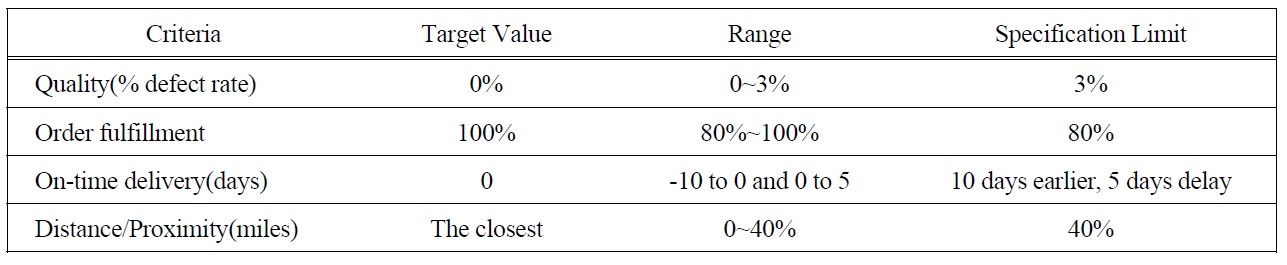
Purchasing risk is measured from four sub-criteria: quality, order fulfillment, on-time delivery, and distance/ proximity. Concerning product quality, DM sets the target value of defect products at zero and the upper specification limit at 3% to indicate the allowable deviation from the target value. Zero loss will occur for 0% defective parts and 100% loss will occur at the specification limit of 3% defective parts. For order fulfillment rate, the loss will be zero for the supplier who fulfills all order quantity (100%) and the total loss will occur if supplier can only satisfy 80% of total order. For on-time delivery, the specification limit of delivery is 10 days and 5 days for early and delay shipment, respectively. The DM will tolerate the shipment for maximum 5 days delay and 10 early. In this case, manufacturer will incur 100% loss if shipment is 5 days delayed or 10 days earlier from scheduled shipment, and on contrary, no loss incurred if
[Table 2.] The Specification Limit and Range Value of Four Sub-criteria.
The Specification Limit and Range Value of Four Sub-criteria.
[Table 3.] Actual Value of the Four Sub-criteria.

Actual Value of the Four Sub-criteria.
the shipment is on time. For distance/proximity, a zeroloss will occur at the closest supplier and the specification limit is up to 40% of the closest supplier. It means that the manufacturer will incur 100% loss if there is other suppliers in consideration whose distance reaches the specification limit. The specification limit and range value of each sub-criterion are presented in Table 2.
Calculating the value of
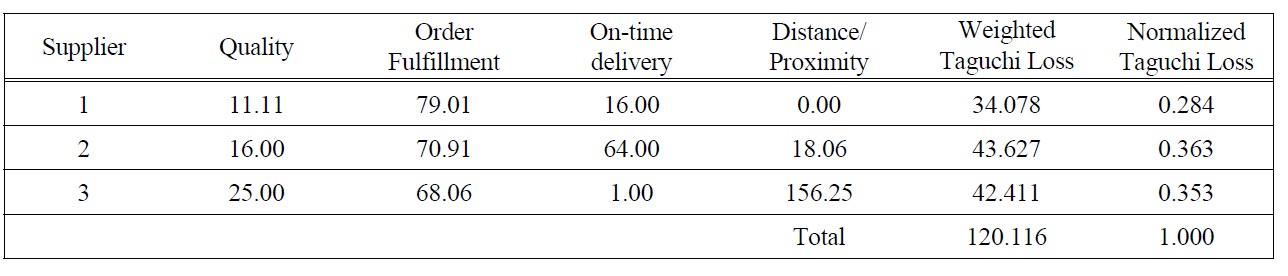
The actual values (Table 3), together with the value of loss sub-criterion
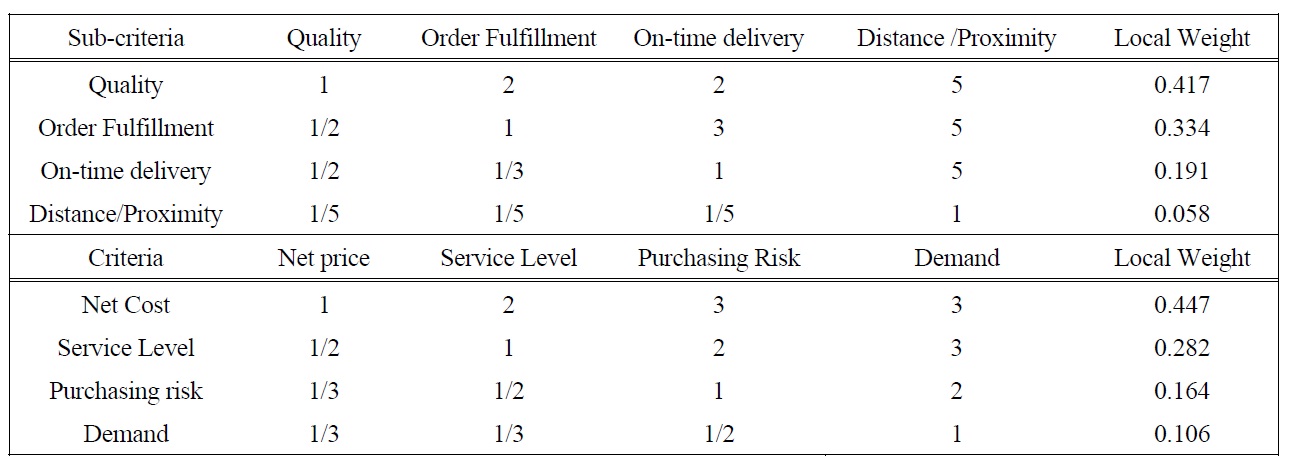
Suppose the pair-wise comparison matrix and local weight for each of these four sub-criteria using AHP is that shown in Table 5. The consistency Ratio (CR) of table 5 is 0.0971 (less than 0.1). The weighted Taguchi loss is then calculated using Taguchi losses and the local weight of sub-criterion. Table 4 shows the weighted Taguchi loss and the normalized Taguchi loss for each supplier. The normalized Taguchi loss is then used as a coefficient of purchasing risk in fuzzy MOLP. Based on suppliers’ data in Table 1 and the normalized Taguchi Loss in Table 4, the fuzzy MOLP supplier selection of the presented problem is constructed according to Eq. (8)-(12) as follow:
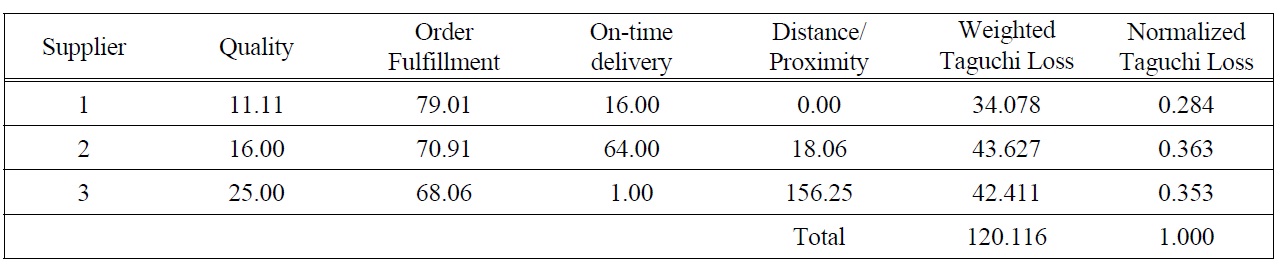
Taguchi Loss.
[Table 5.] Pair-wise Comparison Matrix
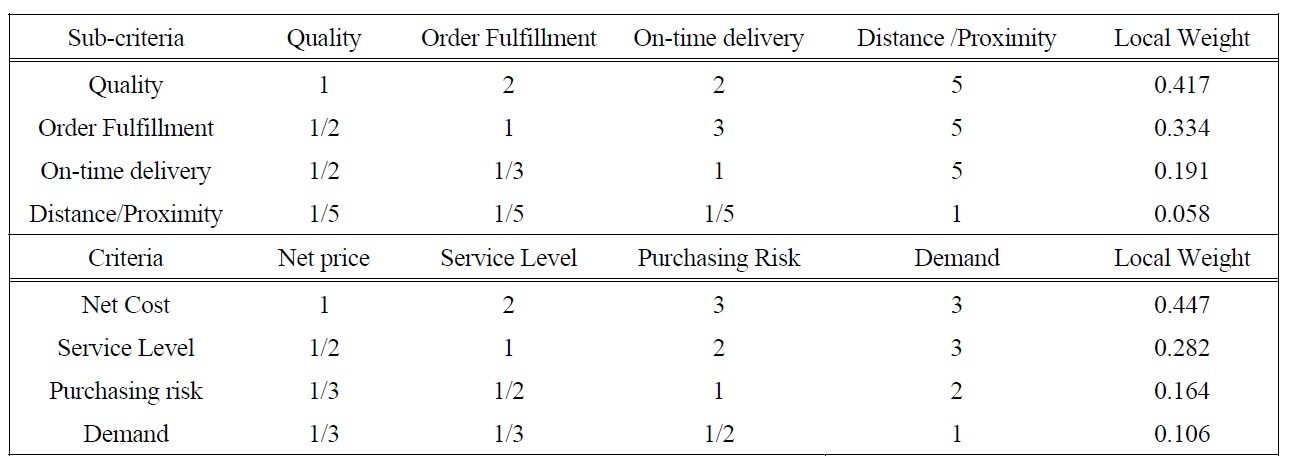
Pair-wise Comparison Matrix
MinZ1 = 10x1 + 12x2 + 9x3 ≤~Z10
MaxZ2 = 0.75x1 + 0.9x2 + 0.85x3 ≥~Z20
MinZ3 = 0.284x1 + 0.363x2 + 0.353x3 ≤~Z30
subject to:
x1 + x2 + x3 ? 1400
10x1 + 12x2 + 9x3 ≤ 20000
x1 ≤ 500, x2 ≤ 600, x3 ≤ 550
xi ≥ 0
The criteria and constraint can be considered equally important and added together for comparison. However, such a comparison is generally unfair due to certain criteria that that may be more important than others. In this model, the weight of cost, service level, purchasing risk and demand are derived from AHP. Table 5 shows the pair-wise comparison matrix and local weights for criteria and constraint. The consistency Ratio (CR) is 0.026 (less than 0.1).
Calculating the membership function using maxmin operator (Eq. (16)) gives 0.566, 0.566 and 0.566 for
Max (1 ? ρ) (0.447λ1 + 0.282λ2 + 0.164λ3 + 0.106γ1) ? p(ε1 + ε2 + ε3 + δ1)
subject to:
12x1 + 16x2 + 12x3 ≤ 20000
x1 ≤ 500, x2 ≤ 600, x3 ≤ 550
ω1 + ω2 + ω3 + β1 = 1
ε1 ≤ 0.566, ε2 ≤ 0.566, ε3 ≤ 0.566, δ1 ≤ 0.847
λ1, λ2, λ3, γ 1 ∈ [0, 1]
x1, x2, x3, ω1, ω2, ω3, β1 ≥ 0
In this problem, the original two-phase approach fails to yield the feasible solution. The constraint associated with
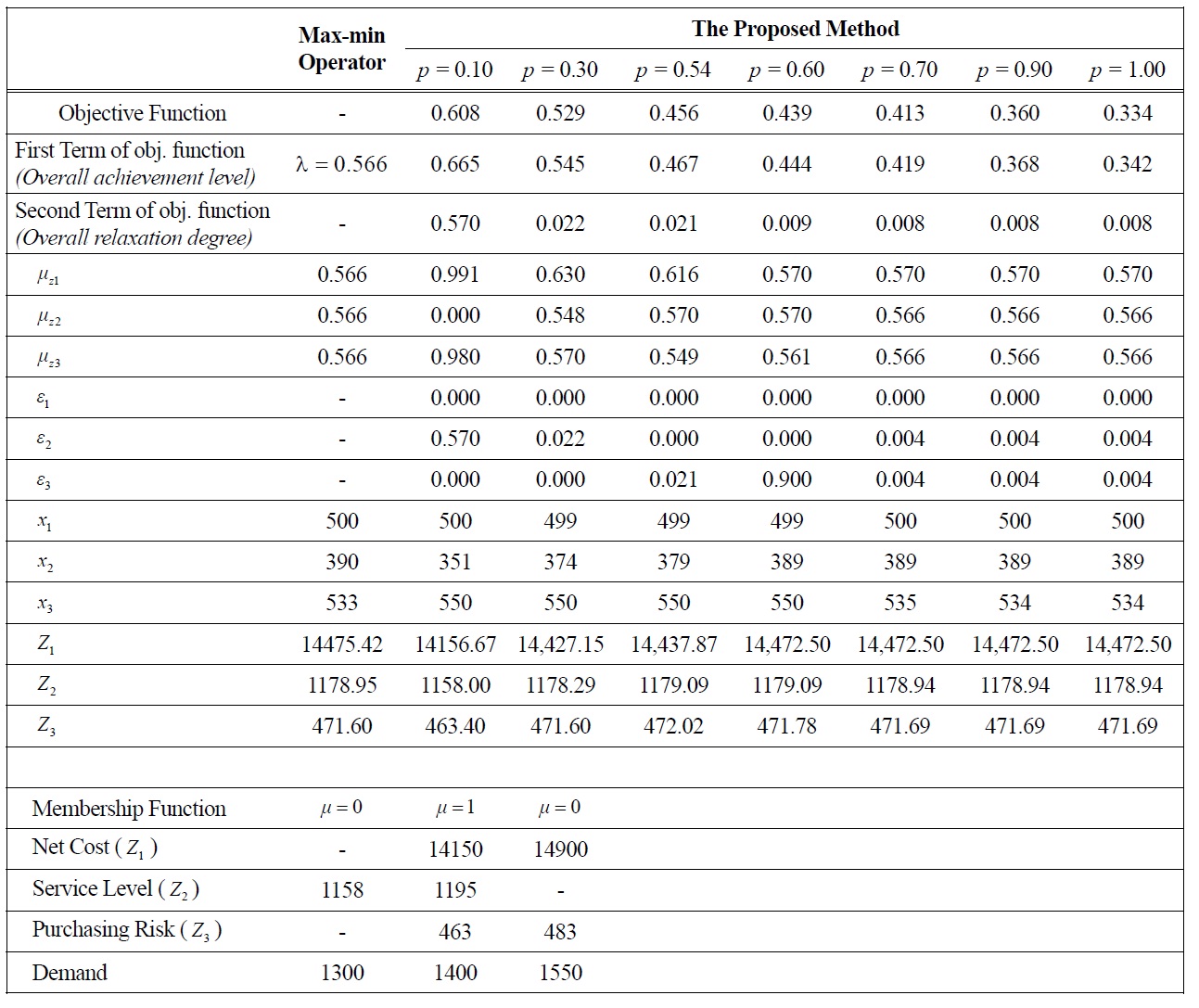
Table 6 provides a set of the feasible solutions resulted by utilizing the proposed method which includes the overall achievement level, individual achievement level, ordering plan and the objective value of the equivalent crisp model along with the upper and lower bounds of fuzzy objectives and constraint. As shown in the Table 6, the overall achievement level of the pro-posed approach is known to be better than that of Maxmin operator (
In this model, the service level (
[Table 6.] Comparison of Max-min Operator and the Proposed Approach.
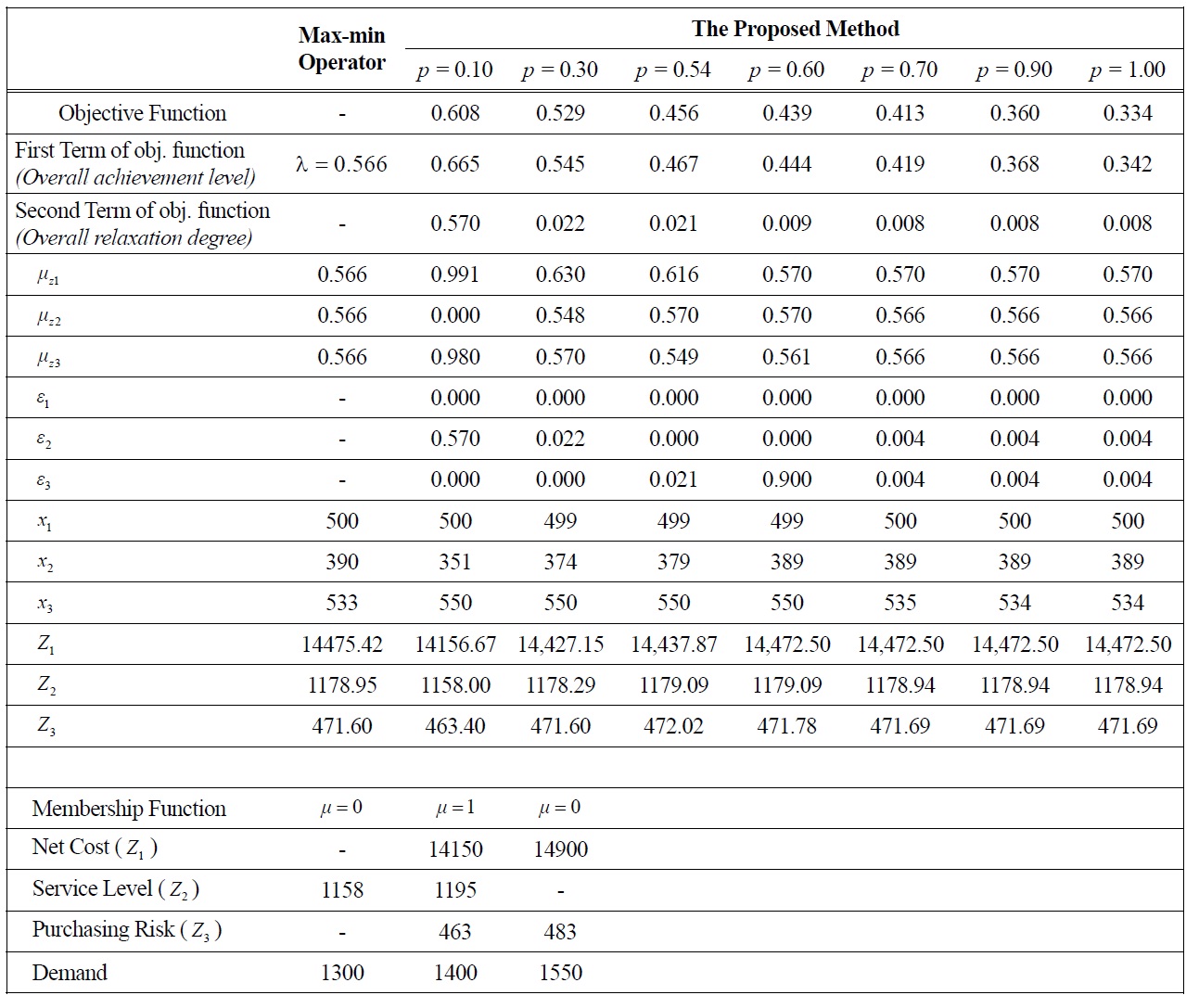
Comparison of Max-min Operator and the Proposed Approach.
0.54 and 0.6. Moreover,
In this fuzzy formulation, all suppliers are selected to supply product to the firm. Moreover, upon more careful observation, it is revealed that ordering to Supplier 1 and Supplier 3 is more preferable. It is indicated from the order quantity assigned to these suppliers as they receive the biggest amount of order quantity which is equal/closer to their full capacity. In this case, it is not profitable to order more quantity to supplier 2 because it offers the most expensive price and the highest purchasing risk among others. As mentioned above, the price (net cost) is put as the main concern of the DM (the highest weight). Thus, placing a smaller order quantity to Supplier 2 is the best decision.
Without loss of generality, suppose that the DM wants to select
Supplier selection is an essential task within the purchasing function that needs careful screening under some qualitative and quantitative criteria. Moreover, most information required to assess supplier is usually not known precisely and typically fuzzy in nature over the planning horizon. Concerning such characteristics, this research proposes integrated methodology for FMOLP model for supplier selection. In formulated problem, the most common fuzzy objectives and parameter in practical ordering decision have been presented. AHP is used to avoid the subjective judgment on qualitative/quantitative criteria and TLF is employed to quantify the purchasing risk. For the purpose of solving the FMOLP problem, the enhanced two-phase fuzzy programming model has been developed. Through numerical experiment, we demonstrate the promising advantage of our proposed approach over the max-min operator (Zimmermann’s approach). Finally, this integrated approach provides a set of potential feasible solutions which guide DMs to select the best solution according to their preference. This also refers to a multi-objective optimization problem that should be concerned in future studies.