In this paper, an interactive planning and scheduling framework are proposed for optimising operations from pits to crushers in ore mining industry. Series of theoretical and practical operations research techniques are investigated to improve the overall efficiency of mining systems due to the facts that mining managers need to tackle optimisation problems within different horizons and with different levels of detail. Under this framework, mine design planning, mine production sequencing and mine transportation scheduling models are integrated and interacted within a whole optimisation system. The proposed integrated framework could be used by mining industry for reducing equipment costs, improving the production efficiency and maximising the net present value.
Nowadays, mining activities take place all over the world and become a major source of a country’s natural wealth. Modern mining is very complicated procedure that may sustain over many years and necessitate huge expenditure. To maximise the profit and the utilisation of mine reserves while providing a better development program, a good mining plan/schedule must not only meet both the long-range and long-term mining requirements but also satisfy many practical details that are unique to day-to-day operations. The operation of a mine is an enormous and complex task, particularly for mines having a life of many years. According to the recent literature survey, Operations Research (OR) techniques (Newman
Mining is the process of excavating the natural minerals such as metallic ore (iron), non-metallic ore (phosphate) and fossil fuels (coal) from the earth’s crust. Mining methods is mainly divided into two groups: open-pit mining and underground mining. Most of the world’s ore mineral is extracted by open-pit mining, especially in Australia. In this paper, we focus on the integration of open-pit mine design, mine production and pits-to-crushers transportation under an interactive planning and scheduling optimisation framework.
1.1 Literature Review on Mine Design Planning
The fundamental and vital mining problem is to determine the contours of an open-pit mine (blocks of a mine), based on geological data and engineering feasibility requirements to yield maximum possible net income. The problem of determining the optimum ultimate pit limits (contours) of a mine is called
As pioneers, Lerchs and Grossmann (1965) present to the mining community an algorithm to find the optimum design for an open-pit mine. Two numerical methods are proposed to determine the pit contour with the maximum profit: a simple dynamic programming algorithm for the 2D pit and a more complicated iterative algorithm (known as Lerchs-Grossmann algorithm) for the 3D pit. However, the Lerchs-Grossmann algorithm is vague due to the lack of mathematical validations. Caccetta and Giannini (1994, 1998) present several mathematical theorems in their implementation and development of Lerchs-Grossmann algorithm. Their work is helpful in explaining the structure and characteristics of Lerchs-Grossmann algorithm. Underwood and Tolwinski (1998) transform the Lerchs-Grossmann approach by mathematical programming settings. Thus, the minedesign graph model is represented by matrices and solved by generic linear programming formulation. A dual simplex approach is developed and compared with Lerchs- Grossmann algorithm by validating some mathematical lemmas and remarks. Their academic contribution is to provide an interpretation of the network flow graph theoretic methodology from a mathematical programming viewpoint. By formulating the open-pit mine as the maximum closure of a directed network flow graph, the mine design problem is actually equivalent to the maximum flow or the minimum cut problem. For the maximum flow problem, there are a number of efficient algorithms that have been developed over the last decade. Relating to implementation and performance analysis for the mine design problems, Hochbaum and Chen (2000) present a detailed study of the push-relabel algorithm as compared to the Lerchs-Grossmann algorithm.
Nowadays, the open-pit mine design planning problem has been widely studied since the pioneering work of Lerchs and Grossmann (1965). Due to its simplicity and usefulness, the 2D (3D) block models and Lerchs- Grossmann-type approaches (including subsequent extensions and improvements) have been commonly used by most off-the-shelf commercial mining software packages for open-pit mine design and long-term planning.
1.2 Literature Review on Mine Production Sequencing
To distinguish the problem types, the problem for determining the sequence of the blocks (or benches) over time periods is called
Many researchers indicate that large size of realworld cases has made the mine production MIP model intractable for use, thus leading to the development of numerous heuristic methods. The following papers address heuristic approaches for mine production sequencing problems. Cullenbine, Wood and Newman (2011) recently develop a sliding-time-window heuristic for the open-pit mine block sequencing problem. This heuristic algorithm uses an “earliest start time” or “earliest extraction period” for each block under maximum production and maximum processing capacities. However, the proposed heuristic approach cannot guarantee to find a feasible solution of sub-models because of assumptions and relaxed variables. Myburgh and Deb (2010) report an application of evolutionary algorithm for mine production sequencing. In their proposed evolutionary optimisation procedure, a starting feasible sequence of blocks represented as a chromosome is iteratively improved by genetic operators such as crossover and mutation. However, it is unclear how the feasibility of neighbouring solutions can be guaranteed subject to constraints of precedence relationships, resource capacities and time periods. Ramazan (2007) develops a so-called “Fundamental Tree Algorithm” with LP to aggregate a subset of blocks as branched trees. This algorithm is useful to reduce number of integer variables and number of constraints required within the MIP formulation for mine production sequencing. However, the author cannot further propose a heuristic algorithm to solve the relaxed MIP model. Kumral and Dowd (2005) develop a simulated annealing (SA) metaheuristic to deal with mine production sequencing. In their method, optimisation procedure is carried out in two stages. In the first stage, Lagrangian relaxation is applied to obtain an initial suboptimal solution. Then, SA algorithm is implemented to improve the initial sub-optimal solution further. However, it is hard to justify the correctness of this method because the detail of constructing a feasible solution is not provided in the paper. Tolwinski and Underwood (1996) propose a guided-search heuristic algorithm to find a path with maximum value in an acyclic direct graph. Then, this so-called path-generation procedure is developed to determine the sequence of blocks based on the value-based decision rule. However, solutions of large-size realistic instances may be quite far away from optimality.
1.3 Literature Review on Mine Transportation Scheduling
Compared to mine design and mine production models, a limited amount of research interests focus on optimising mine transportation. Choi and Nieto (2011) propose a modified least-cost path algorithm for the optimal haulage routing of off-road dump trucks in construction and mining sites. Topal and Ramazan (2010) apply MIP to minimise maintenance cost of mining equipment such as trucks over a multi-year time horizon. Souza
According to the above literature review, most research results in the literature concentrate on mine design (selection of blocks) models and mine production (sequencing of blocks) models, with the objective function of maximising the net present values. However, the decision variable in these models is binary that equals one if one block is mined in given periods or zero otherwise. In other words, these models cannot efficiently determine the timing elements (e.g., starting time, completion time and tardiness) of operations in an algorithmic way. Most mine transportation problems aim at minimising the equipment cost (e.g., trucks) of fleet management using planning algorithms such as leastcost- path analysis. In real-world applications, mine transportation models should be tightly integrated with mine design and mine production problems to achieve the overall efficiency improvement. Therefore, the main purpose of this paper is to optimise the pits-to-crushers mining operations and investigate an interactive framework of mine design planning, mine production sequencing and mine transportation scheduling for optimising these mining operations within a whole system.
2. MINING OPERATIONS FROM PITS TO CRUSHERS
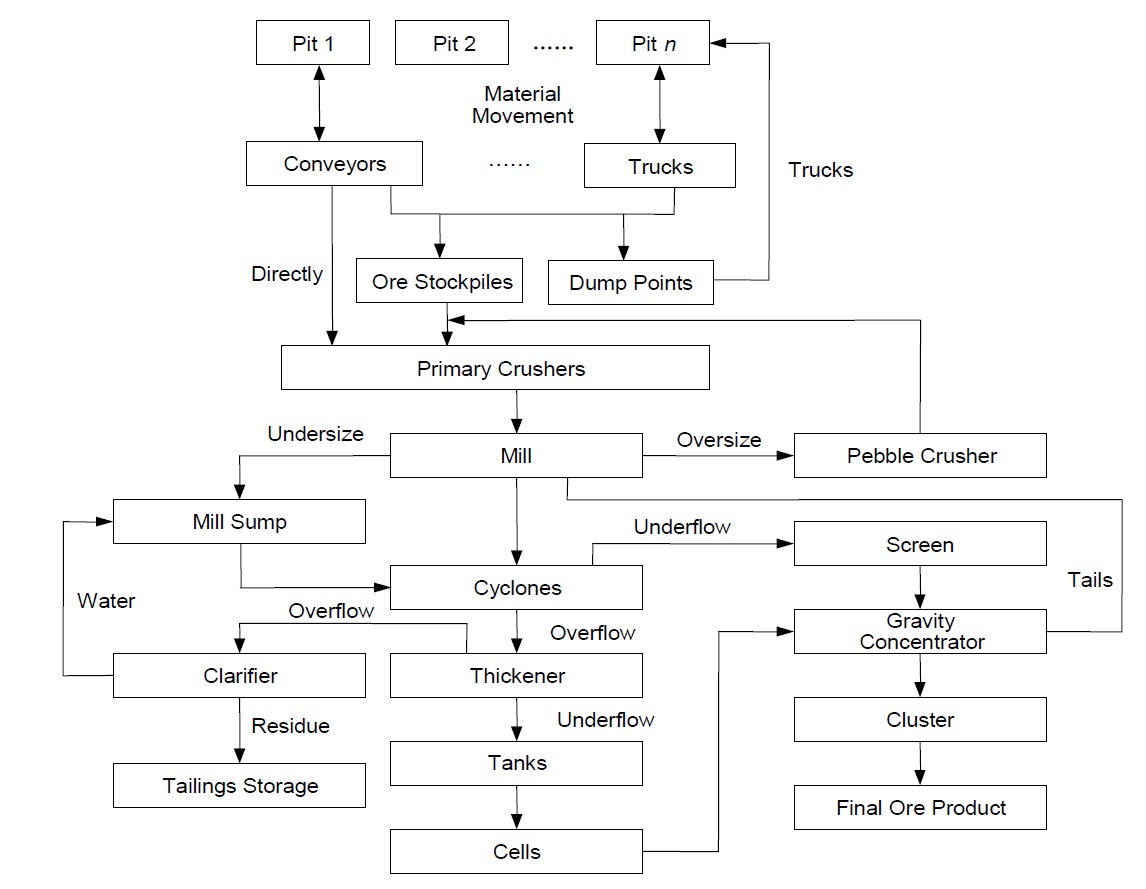
According to our observations at the Australian iron ore mine sites, the practical overall flow process of openpit mining operations has been grouped as follows. In the first step, a set of blocks are selected by the mine design planning model. In the second step, the operation of vegetation clearing may be executed. After vegetation clearing, top soil is removed by loaders and trucks in the third step. In the fourth step, each block is drilled for the purpose to collect the blasting block samples. In the fifth step, the ore samples collected in drilling operations are sent to laboratories for checking the ore properties such as ingredients, grade and density. In the sixth step, the Mobile Processing Units (MPUs) provides leading explosive equipment and blasting services.
After blasting, the ore and waste rocks of a chosen subset of blocks in an open-pit mine are excavated and transported by trucks to the crusher directly if it is high grade, or to blended stockpiles if it is low grade, or to the dump points if it is waste. The ore is then crushed in a semi-autogenous grinding (SAG) mill in an open circuit. More details of the overall ore movement and processing procedure are described in Figure 1.
Thus, the following three types of models for mine design planning, mine production sequencing and mine transportation scheduling are developed and integrated to optimise the mining operations from pits to crushers. For better understanding, the brief description and definition of mine design planning, mine production sequencing and mine transportation scheduling are presented in the following sections.
2.1 Mine Design Planning Module
To design a pit, the entire volume is subdivided into blocks and the value of the ore in each block is estimated by geological information. Precedence relationships of blocks must be satisfied because they are the most critical constraints to specify slope requirements of the pit and to guarantee engineering feasibility requirements.
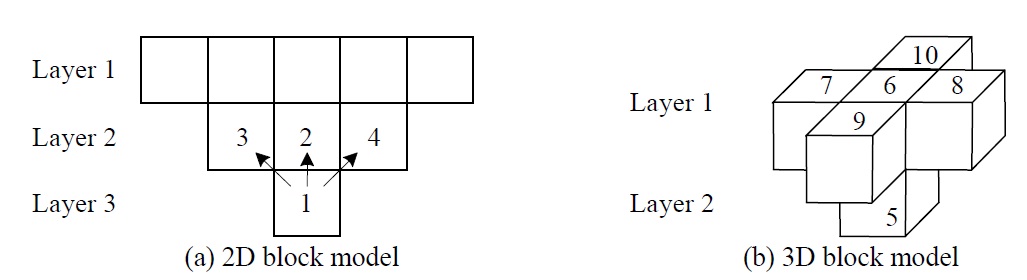
Figure 2(a) illustrates the precedence relationship of a 2D block model for mine design. In most cases, it is assumed that the pit slope cannot exceed 45 degree, which thus means that a block (block 1) cannot be mined until the one (block 2) located directly above it and its two immediate neighbours (blocks 3 and 4) have been removed. Obviously, the 3D block model is much more complicated than the 2D block model because of more complicated precedence relationships.
Figure 2(b) illustrates the precedence relations of a 3D block model, in which a block (block 5) cannot be extracted until the blocks (i.e., blocks 6, 7, 8, 9 and 10) on the level directly above and one of four blocks facing this block on the same level (i.e., one of four blocks directly under blocks 7, 8, 9 and 10) have been excavated.
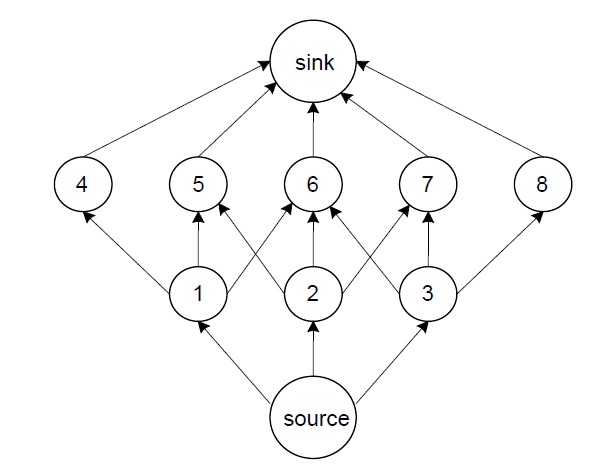
Subject to these constraints, the objective is to determine the closed subset of blocks that maximise the net present value. Illustrated in Figure 3, the open-pit mine design problem can be represented by a directed
network flow graph
In this graph, precedence constraints determined by
The basic mine design planning problem has been modelled as a linear programming model as below.
V a set of nodes (blocks) in a directed network flow graph
A a set of conjunctive arcs in a directed network flow graph
bj weigh of node j that corresponds to block j
xj a binary variable that is 1 if node j is chosen, and 0 otherwise.
Constraint (2) ensures that if node
As pioneers, Lerchs and Grossmann (1965) present to the mining community an algorithm to find the optimum design for an open-pit mine. The planning of a mining program involves the design of the ultimate shape of this open surface. They show that an optimal solution of the mine design problem is equivalent to finding the maximum closure of a directed network flow graph model. Two numerical methods are proposed to determine the pit contour with the maximum profit: a simple dynamic programming algorithm for the 2D pit and a more complicated iterative algorithm (known as Lerchs-Grossmann algorithm) for the 3D pit.
More details about solution techniques for mine design planning models can be found at Lerchs and Grossmann (1965), Caccetta and Giannini (1998), Underwood and Tolwinski (1998) and Hochbaum and Chen (2000).
2.2 Mine Production Sequencing Module
After a given subset of blocks is selected by the mine design planning model, the purpose of mine production sequencing problem is to decide when they should be extracted over certain periods.
With regard to mine production sequencing, the MIP model proposed by Caccetta and Hill (2003) has been well known in mining industries and received considerable attention. The objective of this MIP model is to maximise the profits in certain periods over which the blocks are sequenced. The following constraints are considered in their MIP model: a block is removed in one period only; the precedence relationships between blocks are satisfied; the ore tonnage of each block equals milling capacity in each period; the amount of ore that is milled in each period is between the predetermined lower bound and upper bound values; the tonnage of waste removed does not exceed the prescribed upper bounds. The decision variable
is a binary variable that equals one if block
According to our analysis, the cost functions are primarily reflected by timing factors (i.e., ready times, starting times, completion times, flowtimes, tardiness) of jobs in the sequencing/scheduling model. Thus, the objective of maximising the profits over a time horizon is equivalent to the objectives of minimising the maximum completion time, the mean weighted flowtime and the mean weighted tardiness if the due dates of each block are given.
Therefore, to solve the mine production sequencing problem in a more standard and convenient way, we are exploring to model it as a standard single-stage sequencing problem with special mining production constraints and cost functions.
The mathematical formulation model for a basic single-stage mine production sequencing problem is presented below.
J a set of n blocks to be mined; a block is equivalent to a job in this single-stage sequencing model.
rj release dates of job j, j ∈ J; equivalently it is the earliest available time of block j that is determined by the precedence relationships of blocks.
pj processing time of job j, j ∈ J; equivalently it is the mining time of block j.
dj due dates of job j, j ∈ J; equivalently it is the required finishing time of block j that is determined by the demand of a crusher mill.
wj weight of job j, j ∈ J; equivalently it is the ore value of block j.
L a sufficiently large number.
Sj starting time of job j, j ∈ J; equivalently it is the time point when block j starts to be mined.
Cj completion time of job j, j ∈ J; equivalently it is the time point when block j has been mined and removed from a pit: Cj = Sj+Pj.
Cmax the maximum completion time or makespan: Cmax = maxj Cj.
Fj flowtime of job j, j ∈ J; equivalently it is the total amount time of block j that spends in the system: Fj = Cj - rj.
Tj tardiness of job j, j ∈ J; which is the lateness of block j if it fails to meet the due date, or zero otherwise: Tj = max {0, Cj - dj}.
xij a binary variable that is 1 if job i precedes job j or 0 otherwise.
The objective of this mine production sequencing model is to minimise the total cost that is determined by a function associated with the maximum completion time, the weighted mean flow time and the weighted mean tardiness.
Equation (5) restricts that the completion time of each job should be no earlier than the makespan.
Equation (6) restricts that the starting time of each job should be greater than or equal to the release date.
Equations (7, 8) define the precedence relationship between any pair of jobs
Our proposed model will differ from the current mine production MIP sequencing models in the literature in accordance with the following distinct characteristics. Firstly, our proposed methodology for mine production sequencing problems is based on machine scheduling theory in the literature. Secondly, the objective functions of our proposed model are associated with the maximum completion time, the weighted mean flowtime or the weighted mean tardiness. Thirdly, the decision variables are timing factors such as starting times, completing times, flowtimes and tardiness. Fourthly, our proposed model is more flexible to be extended to deal with more complex scenarios in a standard way.
2.3 Mine Transportation Scheduling Module
Mine transportation problem could be modelled as a special type multi-resource multi-stage scheduling model with a variety of mining constraints such as the limited number of trucks, the fixed transportation routes, etc.
Such a generic and sophisticated multi-resource multi-stage scheduling model for optimising the transportation operations from pits to crushers is being proposed and analysed by an extended disjunctive graph model. The objective functions of this mine transportation scheduling problem are to minimise the maximum completion time or minimise the number of mining equipments in a time window.
In this disjunctive graph, the conjunctive arcs for the fixed production sequences of blocks in a pit are determined by the mine production sequencing module and the mine design planning module, as explained above. In addition, the other sets of conjunctive arcs are determined by the fixed bi-directional transportation routes (e.g., pit to stockpiles, pit to dump points, pit to crushers, stockpiles to pit, dump points to pit, crushers to pit). The transportation routes could be determined by the shortest- path (or least-cost-path) algorithm with the help of GIS and the analysis of planning network graph.
To build the feasible mine transportation scheduling model, the output results of mine design planning model and mine production sequencing model are very important as they are used as the input data to set up the conjunctive arcs for this disjunctive graph model. As a result, this multi-resource multi-stage scheduling model must incorporate the results of the mine design planning problem and mine production sequencing problem with the development of an extended disjunctive graph model.
The definition of disjunctive arcs is also important to determine the feasible solution of mine transportation. In a sense, determining a schedule corresponds with selecting one direction for each pair of disjunctive arcs and discarding the redundant arcs so that obtained schedule leads to the optimal objective function value. The details of mine transportation scheduling will be reported in another paper.
3. INTERACTIVE MINING OPTIMISATION FRAMEWORK
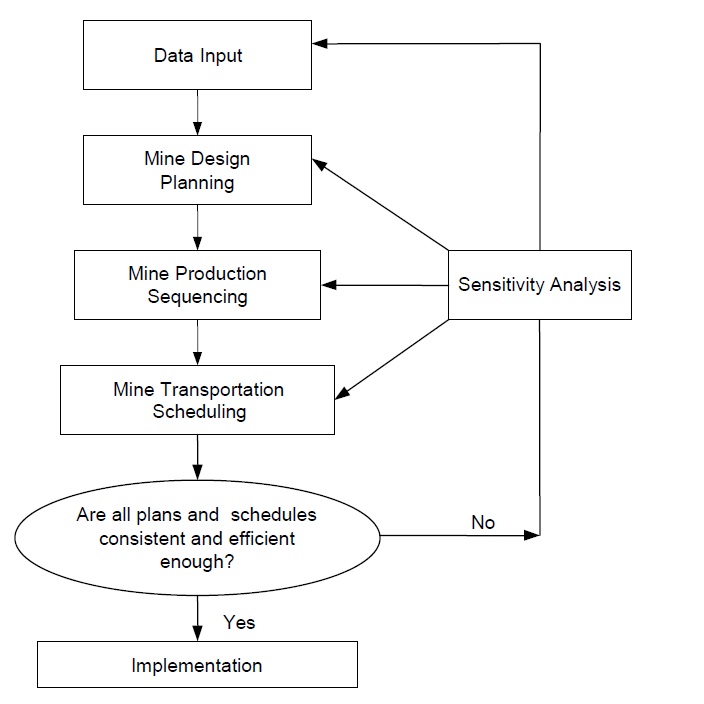
For improving the overall efficiency of ore mining systems, an interactive optimisation framework for mining industry is proposed in this paper. This framework has an interactive mechanism that allows interactive feedback among the mine design planning, mine production sequencing and mine transportation scheduling modules. This feedback mechanism enables the optimisation process to go through several iterations, for the purpose of supporting better decision makings and improving the solution quality by updating input data interactively.
To construct this framework, the first important thing is to clearly distinguish mine design planning, mine production sequencing and mine transportation scheduling. In the literature, mine design planning and mine production sequencing problems are easy to be confused. The mine design problem is a “
According to sequencing and scheduling theory (Baker, 1974), “the pure sequencing problem is a specialised scheduling problem in which an ordering of the jobs completely determines a schedule” (see the first sentence in Page 10, “
Within the proposed interactive planning and scheduling framework, mine design planning problems differ from mine production sequencing/mine transportation scheduling problems in numerous ways.
Firstly, time horizons of most mine design planning problems are long-term or long-range. In contrast, mine production sequencing models are usually defined over a mid-term time horizon. In a long-term time horizon that is commonly over two years, the mining industry would be interested in making strategic decisions whether to explore a mine and how to determine the contours (block models) of this mine to maximise the longterm net present value. In contrast, mid-term time horizon for mine production usually has a time frame of three months to two years. From a tactical viewpoint, the mine industry commonly needs to aggregate the production targets by selecting the set of blocks (benches) to be mined in this mid-term horizon for satisfying midterm export demands. The decisions made by mine transportation scheduling models are operational decisions in a short-term horizon. As such, these day-to-day decisions tend to be of the very specific focus on narrow entities over short time intervals.
Secondly, mine design planning is mainly concerned about the optimum selection of blocks’ subsets in a pit and allocating the limited resources for minimising total costs. The unit measured in planning decision variables is often a cost unit. In comparison, the objective of mine production models is fundamentally associated with the functions of completion times of the jobs and the unit measured in decision variables is often a time unit.
Thirdly, most mine design planning problems are simplified and modelled as a linear programming model or nonlinear programming model, while most mine production sequencing/mine transportation scheduling models include more real life constraints and real time elements and they are usually NP-hard.
Finally, for most mine sequencing/scheduling problems, the scope is considerably narrower with regard to time as well as space, but the level of details taken into considerations is much higher.
Under various practical circumstances, there may be a specified reason necessitating a feedback between planning, sequencing and scheduling modules. For example, a disruption in the mine design planning module (e.g., cancellation of some selected blocks to be mined due to volatile demands) may be of such magnitude that it not only affects its facility (e.g., a pit) where it occurs and other facilities (e.g., stockpiles and crushers) as well. In this situation, the results of short-term mine transportation scheduling module may further indicate that the data from the output of long-term mine design planning or mid-term mine production sequencing modules may turn to imprecise or inaccurate. As a result, the original mine design planning or mine production sequencing procedures may need to be updated and reconstructed in an interactive way.
A generic framework with a feedback mechanism, which allows the overall mine planning and sequencing/ scheduling processes (i.e., mine design planning, mine production sequencing and mine transportation scheduling) to regularly communicate and iterate, is elucidated in Figure 4.
In such a framework, the output results of the longterm mine design planning model could serve as the input data to the mid-term mine production sequencing process. The output results of mine production sequencing model could be applied as the input data to the mine transportation scheduling model. Obviously, such an interaction between a mine planning module and a mine scheduling module may be sophisticated in real-world scenarios. However, they are able to be integrated, share information and interact reactively with one another.
The proposed interactive mining optimisation framework has many merits:
In this paper, an interactive framework is proposed for optimising the operations from pits to crushers in ore mining industry. Under this framework, the mine design planning problem, the mine production sequencing problem and the mine transportation scheduling problem are investigated and integrated within a whole mining optimisation system. The mine design planning problem can be modelled as a linear programming model or a directed network flow graph model and solved by traditional solution techniques such as Lerchs-Grossman algorithm or the maximum flow algorithm. A new mine production sequencing model is proposed, which is based on single-stage sequencing theory with special mining production constraints and associated cost functions. This approach is different from most current mine production MIP sequencing models in the literature. Using the results of long-term mine design planning and midterm mine production sequencing as input data, a complicated multi-resource multi-stage scheduling model is developed and analysed by an extended disjunctive graph for optimising the short-term truck transportation operations from pits to crushers.
In the direction of future study, the collection of real-world data, the development of integrated solution algorithms and the implementations in realistic mine sites are essential to validate the proposed methodology.