The fixed charge transportation problem (FCTP) is an extension of the (linear) transportation problem (TP). Since the fixed charge problem was initialized by Hirsch and Dantzig (1968), it has been widely applied in many decision making and optimization problems. Interested readers may refer to Sun
It is well-known that the TP is one of the important traditional optimization problems, and it has also been widely applied in real-life such as distributing systems, job assignment and transportation. In the traditional TP, there are two kinds of constraints: source constraint and destination constraint. There are many efficient algorithms for solving the traditional transportation problems such as Balinski (1961) and Srinivasan and Thompson (1972). As an extension of the traditional TP, the solid transportation problem (STP) was introduced by Haley (1962) and Li
This paper consists of 6 sections, and its frame is organized as follows: In section 2, some basic concepts and properties in uncertainty theory used throughout this paper are introduced. In section 3, an uncertain FCTP model is constructed. In section 4, according to uncertainty theory, the model can be transformed to its deterministic form, and then we can use the classical method to find its solution. A numerical example is given in section 5. A brief summary is presented in section 6.
In order to deal with human uncertainty, an uncertainty theory was established by Liu (2007), and refined by Liu (2010b), which is a branch of mathematics based on normality, duality, subadditivity, and product measure axioms. Since then significant work has been done by researchers based on the uncertainty theory both in theoretical and practical aspects. In theoretical aspect, Liu (2008) proposed an uncertain process which is a sequence of uncertain variables indexed by time or space and uncertain differential equation which is a type of differential equation by canonical process in 2008. Liu (2009a) established uncertain calculus to deal with dynamic uncertain phenomena in 2009. Besides, the concept of uncertain logic was proposed by Li and Liu (2009) to describe uncertain knowledge, uncertain inference was introduced by Liu (2010a) via conditional uncertain measure. Meanwhile, some other theoretical properties of uncertain measure are studied (Gao, 2009; You, 2009). In practical aspect, Liu (2009b) designed uncertain programming that is a type of mathematical programming involving uncertain variables, which has been used to model system reliability design, project scheduling problem, vehicle routing problem and facility location problem. Now, the uncertainty theory has become a mathematical tool to model the indeterminate phenomenon in our real world. In this paper, the uncertainty fixed charge transportation problem (UFCTP) is modeled based on the uncertainty theory. We shall first introduce some information about the uncertainty theory.
Theorem 1: (Liu, 2010b) Let ξ1, ξ2, …, ξn be independent uncertain variables with uncertainty distribution Φ1, Φ2, …, Φn, respectively. If
ξ =
is an uncertain variable with inverse uncertainty distributions
Theorem 2: (Liu, 2010b) Let ξ1, ξ2, …, ξn be independent uncertain variables with uncertainty distribution Φ1, Φ2, …, Φn, respectively. If
ξ =
is an uncertain variable with inverse uncertainty distributions
Theorem 3: (Liu, 2007) Let ξ and η are independent uncertain variables with expected values. Then for any real numbers
3. FIXED CHARGE TRANSPORTATION MODEL
Let
Then the FCTP can be formulated as follows:
where
In this model, the first constraint implies that the total amount transported from source
In this paper, we assume that the direct cost, the fixed charge, the capacity of each source and each destination are all uncertain variables and denoted by ξ
Where
The main idea of the uncertain programming model is to optimize the expected value of objective function under the chance constraints.
Definition 1: Assume that
M {
for
A solution
for any feasible solution
We may construct the model of the uncertain fixed charge transportation problem as follows:
In the above model β
We can see that there are many uncertain variables in the above models. In order to find the best solution, we must compute the expected value or uncertain measure. If the uncertain variables are complex, computing objective value is actually a time-consuming work. So it is better for us to transfer the model into its crisp equivalence. In this section, we shall induce the crisp equivalence of model under some special conditions.
Theorem 4: Assume that ξ
respectively, then the model (2) is converted to equivalence model:
Proof: By using the linearity of expected value operator, we can easily prove this theorem, i.e., since ξ
respectively, then
where
So the model (3) is converted to equivalence model:
Note that model (4) is a deterministic programming model.
In order to show the application of the model, we shall present an example of coal TP in this section. Coal is a crucial energy source in the development of economy and society. Accordingly, how to transport the coal from mines to the different areas economically is also an important issue in the coal transportation. For the convenience of description, we summarize the problem as follows. Suppose that there are four coal mines to supply the coal for six cities. During the process of transportation, two kinds of conveyances are available to be selected, i.e., train and cargo ship. Now, the task for the decision-maker is to make the transportation plan for the next month. At the beginning of this task, the decision maker needs to obtain the basic data, such as supply capacity, demand, transportation cost of unit product, and so on. In fact, since the transportation plan is made in advance, we generally cannot get these data exactly. For this condition, the usual way is to obtain the uncertain data by means of experience evaluation or expert advice. Assume that all uncertain variables are normal uncertain variables, in which we suppose:
then the model (4) is equivalent to the following model:
And the associated uncertain data are listed in the following Tables 1-4,
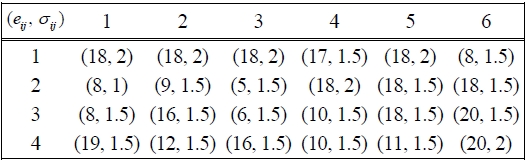
[Table 1.] Parameters of normal distribution N(eij, σij) of direct costs
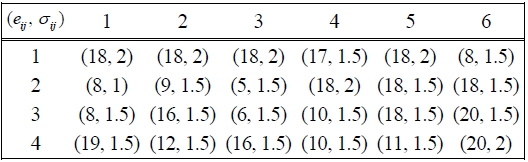
Parameters of normal distribution N(eij, σij) of direct costs
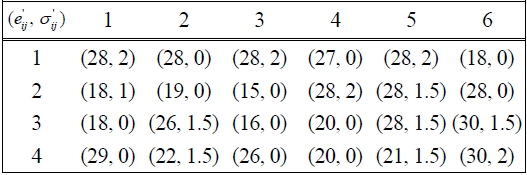
[Table 2.] Parameters of normal distribution N(e'ij, σ'ij ) of fixed charges
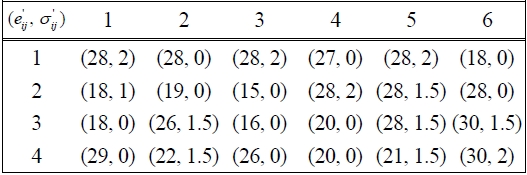
Parameters of normal distribution N(e'ij, σ'ij ) of fixed charges
[Table 3.] Parameters of normal distribution N(ei, σi) of supplies

Parameters of normal distribution N(ei, σi) of supplies
[Table 4.] Parameters of normal distribution N(ei', σi') of demands

Parameters of normal distribution N(ei', σi') of demands
We also suppose the confidence level is β
x15 = 1.325328, x16 = 11.21139, x22 = 13.21139,
x23 = 12.97152, x31 = 11.81709, x33 = 8.239877,
x34 = 7.520246, x44 = 11.81709, x45 = 13.88607.
This paper mainly investigated the uncertain fixed charge transportation problem based on an uncertainty theory, and an uncertain model was constructed. By applying the uncertainty theory, the uncertain model can be transformed to a deterministic form, and then we can find its solution by the classical method. Finally, as an application of the model and algorithm, we presented a coal transportation problem as example, and the result showed that the proposed uncertain cost transportation problem model works well.