Identity-based cryptography encrypts the message with the user’s identity including the name and e-mail address. An identity-based encryption (IBE) scheme can restrict an authority to indicate the identity of the recipient [1, 2]. Attribute-based encryption (ABE) was published by Sahai and Waters [3]. Unlike IBE, the message is encrypted with attributes, such as gender, age, and affiliation, so ABE schemes can designate the recipients by assigning common attributes of others. ABE consists of two policies. The first is the key policy ABE (KP-ABE) in which each private key is associated with an access structure [4]. The other scheme is the ciphertext policy ABE (CP-ABE), in which a ciphertext is associated with an access structure [5-7]. The attribute-based proxy re-encryption scheme (ABPRE) extends traditional proxy re-encryption to its attribute-based counterpart. Therefore, the capability of delegation is transferred to the designated users [8]. However, the previous ABPRE does not provide a constant length of message and number of pairing operations. Recently, a constant ciphertext length based CP-ABE was proposed by Emura et al. [9]. The computation cost and ciphertext length were reduced significantly compared to previous papers. However, the encryption scheme over ABPRE has not been proposed yet. For this reason, in the present paper, we propose a new constant computation-based ABPRE. The scheme utilizes the capability of delegation with constant pairing operations.

The rest of this paper is organized as follows. In section II, we describe ABPRE. In section III, preliminaries such as bilinear map and complexity assumptions are introduced to support the construction and the security proof. In section IV, our new ABPRE scheme is introduced and then we analyze security model and computation performance. Finally the conclusion is drawn in section V.

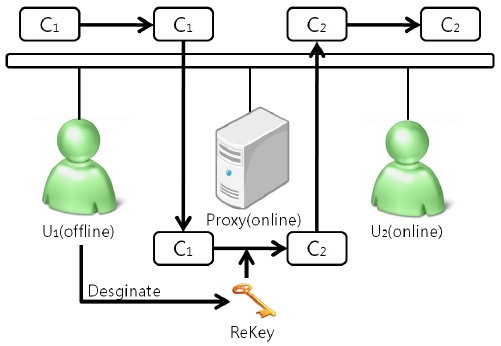
In ABPRE, a user can re-encrypt the ciphertext using a re-key. Detailed relationships are shown in Fig. 1. First U₁ generates the ciphertext C₁, which can be decrypted with U₁’s attributes. One day, U₁ is absent, but we need to read the data from C₁ . In this case, U₁ will store the re-encrypted ciphertext with attributes that represent the specific recipient or groups into a proxy-server. After that, U₂ can access to the proxy-server and then gain the re-encrypted data.

The ABPRE scheme is illustrated in [8, 10]. An ABPRE scheme is comprised of six steps including SETUP, KEYGEN, RE-GEN, ENC, RE-ENC, and DEC.

SETUP: The setup algorithm takes no input other than the implicit security parameter. It outputs the public parameters pp and a master key mk .

KEYGEN (S, mk ): The key generation algorithm takes as input the master key ^mk and a set of attributes S that describe the key. It outputs a private key usk .

RE-GEN (usk , AS): The re-key generation algorithm takes as input the secret key usk and access structure AS . It outputs a re-key rk .

ENC (m, AS): The encryption algorithm takes as input the public parameters pp , a message m, and an access structure AS over the universe of attributes. The algorithm will encrypt m and produce a ciphertext C such that only a user that possesses a set of attributes that satisfies the access structure will be able to decrypt the message. The ciphertext implicitly contains AS .

RE-ENC (rk ,C ): The re-encryption algorithm takes as input the re-key rk and a ciphertext C . First the algorithm checks the index set in rk . If rk satisfies the access structure of C , it outputs a re-encrypted ciphertext C' ; otherwise, it rejects the re-key.

DEC (pp , C , usk ): The decryption algorithm takes as input the public parameters pp , a ciphertext C , which contains an access policy AS , and a private key usk , which is a private key for a set S of attributes. If the set S of attributes satisfies the access structure AS then the algorithm will decrypt the ciphertext and return a message m .

In this section, some definitions which are the basis of attribute-based encryption schemes, including our scheme, are presented.

Definition 1. Bilinear groups and a bilinear map are defined as follows: G and G_T are finite cyclic groups of prime order p . e is an efficiently computable bilinear map or pairing e : G ×G →G_T , with the following properties;

Bilinearity: For any g,h ∈ G , and a,b ∈ Z_p , we have e(g^a ,h^b) = e(g,h)^a·b .

Non-degeneracy: e(g,g) ≠ 1.

Note that e(*,*) is symmetric since e(g^a ,g^b) = e(g,g)^a·b = e(g^b ,g^a) .

Definition 2. Complex Triple Diffie-Hellman (CTDH) problem. Let e : G ×G → G_T be a bilinear map, where G has prime order p and g is a generator of G , random numbers n,a,b,c,d ,R ∈ Z_p . Given a tuple

as inputs, output g^abc .

Definition 3. Augment Diffie-Hellman (ADH) problem. Let e : G × G → G_T be a bilinear map, where G has prime order p and g is a generator of G , random numbers a,b ∈ Z_p . Given a tuple

as inputs, output g^ab .

Definition 4. The CTDH assumption holds in G if no probabilistic polynomial time adversary is able to output g^abc from

with non-negligible advantage, where random numbers n,a,b,c,d ,R ∈ Z_p and generator g ∈ G are chosen independently and uniformly at random.

The CTDH problem is more difficult than the ADH problem; if given the input of the ADH problem

, we could select R + nd = 1,R = ab,b = c and outputs g^Rc from the CTDH oracle with inputs

The CTDH problem is the basis of the master key security in our scheme.

Definition 5. Augment decisional bilinear Diffie-Hellman (ADBDH) problem. Let e : G × G → G_T be a bilinear map, where G has prime order p and g is a generator of G , random numbers a,b,c ∈ Z_p . Given a tuple

as inputs, output 1 if Z = e(g,g)^abc ; otherwise, output 0.

Definition 6. The ADBDH assumption holds in G if no probabilistic polynomial time adversary is able to distinguish the tuples

with non-negligible advantage, where a,b,c,z ∈ Z_p and a generator g ∈ G are chosen independently and uniformly at random.

We adapt a constant number of pairing operations to a previous ABPRE scheme [8]. Whenever the attribute is decided in the scheme, to reflect the attributes, we need to compute the pairing operation with its designated attributes. To reduce the number of pairing operations, we reduce the pairing operation by using an exponential operation which can easily calculate the summation of the exponent. Therefore, we calculate the exponent and then compute the pairing operation just once.

In this scheme we consider the access structure consisting of AND gates between positive and negative attributes. Denote the index set of all the attributes as τ .The access structure is represented as ∧(+d_i , ？d_i )_{i ∈τ} , which are the positive attribute and the negative attribute, respectively. Any user receives a secret key associated with an attribute set S ⊆ τ from the authority. The users can decrypt the ciphertext, if the following conditions of the attribute are met:

If +di appears in AS , then i ∈ S ;

If ？di appears in AS , then i ？ S .

SETUP (1^k ) : A bilinear group G of prime order p ,with bilinear map e : G × G → G_T is generated. Next, it selects elements k ,y ,z ,t_i (1≤ i ≤ 3n) in Z_p and two generators g,h of G at random. Let Y := e(g,h)^y and T_i := g^ti for each 1≤ i ≤ 3n . The public parameter pp includes

The master key mk is < k ,y ,z ,{t_i}_{1≤ i ≤ 3n} > .

KGEN(S,mk) : Let S denote an index set of attributes. It chooses a random r₁,...,r_n from the Z_p and sets r = r₁ + r₂ + ... + r_n . It computes

and for each i ∈ N(N = {1,2,...,n}) : (D_i,1 = h^r_i )_i∈N . This outputs a user’s secret key

ENC(m,AS) : Let AS denote an access structure. To encrypt a message m ∈ G_T , it selects a random s ∈ Z_p and computes

For i ∈ N : if +d_i appears as AS , C_i = T^s_i; if -d_i appears as AS , C_i = T^s_n+i; otherwise, C_i = T^s_2n+i . It outputs

RKGEN(usk, AS') : Let usk denote a valid secret key consisting of

and let AS' denote an access structure. It selects a random d ∈ Z_p and set

For i ∈ N D^'_{i ,1} =D_{i ,1} ·h^d ; C^' is the ciphertext of ？ under the access structure AS' .

It outputs

REENC(rk ,C) : Let rk denote a valid re-key consisting of

and C denote a well-formed ciphertext

This step checks whether S satisfies AS ; if not, output ┻ ; otherwise, for i ∈ N :

+d_i appears in AS ,

？d_i appears in AS ,

Otherwise,

It computes

and

Next it computes E = e(C,D^T ) = e(g,h)^{(n·d+r)(k·s·z)}

It then computes

It outputs a re-encrypted ciphertext

Note that C_re can be re-encrypted iteratively. Thus we would obtain

where C'' is obtained from the REENC algorithm with the input of another rk^' and C^' . The size of the ciphertext and re-encryption times increase linearly.

DEC (C,usk) : Let usk denote a valid secret key

. It checks whether S satisfies AS ; if not, it outputs ┻; otherwise, decrypt.

If C is an original well-formed ciphertext consisting of

, for i ∈ N :

+d_i appears in AS ,

？d_i appears in AS ,

Otherwise,

It computes

and

Next it computes E = e(C,D^T ) = e(g,h)^k·r·s·z

It outputs

Otherwise, if C is a re-encrypted well-formed ciphertext consisting of

, then it decrypts C^' using usk and obtains ？ = g^d . Then it outputs

Otherwise, if is a multi-time re-encrypted well-formed ciphertext, then decryption is similar with the above phases.

Since our scheme is an expansion of a previous ABPRE scheme in [8], the security proof is based on previous proof in [8] and we also extend it to our scheme.

Theorem 1: When the ADBDH assumption holds in (G,G_T) , the ABPRE scheme ensures selective-structure chosen plaintext secure in the standard model.

Proof: In this section, we show that SS-CPA-ABPRE meets the requirements in terms of the ADBDH assumption.

We suppose that an adversary wins the SS-CPA-ABPRE game with a non-negligible advantage ε . A simulator S can be constructed to distinguish D_adbdh from D_rand with the non-negligible advantage

We first suppose the challenger set the groups G and G_T with bilinear map e and a generator g . The challenger randomly selects a side of a fair coin c , without S ’s intervention. If c = true the challenger sets < g,A,B,C,B^' ,Z >∈ D_adbdh ; otherwise it sets ' ,Z >∈ D_rand .

Init: S receives a challenge access structure AS^* , and names I ₊^* ,I _？^* the index set of positive and negative attributes, respectively. Then S chooses x ,y ,α_i ,β_i ,γ_i at random from Z_p for i ∈ N and generates the public key Y = e(A,B )^y . Then S outputs the public parameters as follows:

i ∈ I +* , Ti = gαi ,Tn+i = Bβi ,T2n+i = Bγi ;

i ∈ I ？* , Ti = Bαi ,Tn+i = gβi ,T2n+i = Bγi ;

Otherwise , Ti = Bαi ,Tn+i = Bβi ,T2n+i = gγi.

Phase 1: An adversary A makes several queries to the key generation oracle O_kg , the re-key generation oracle O_rkg , and the re-encryption oracle O_ree .

A makes several queries to the O_kg with an index set I_q . According to the security game, if I_q satisfies AS^* , it outputs ┻.

Otherwise, S queries

from the oracle and outputs usk .

A makes a query to O_rkg with an index set I_q and an access structure AS. According to the security game, if I_q satisfies AS^* , it outputs ┻. Otherwise, S submits I_q to O_kg and obtains a secret key

. S executes the following procedure:

It selects a random d ∈ Z_p and set

For i ∈ N D^' _{i ,1} = D_{i ,1} ·h^d , it outputs

, in which C' is the ciphertext of ？ under the access structure AS'.

A makes a query to O_ree with an index set I_q , an access structure AS', and a ciphertext

According to the security game, if I_q satisfies AS^* , it outputs ┻. If I_q does not satisfy AS, it outputs ┻. Then S submits (I_q ,AS') to the re-key generation oracle and obtains

. S uses rk to re-encrypt the ciphertext C . For i ∈ N :

+d_i appears in AS,

？d_i appears in AS,

Otherwise,

.It computes

, and

Next it computes E = e(C,D^T ) = e(g,h)^{(n·d+r)(k·s·z)}

Finally, it computes

It outputs a re-encrypted ciphertext

Challenge: A submits two equal messages M₀ and M₁ in length. S produces a challenge ciphertext:

Phase 2: Same procedure as Phase 1.

Guess: A tuple was given from D_adbdh when S outputs c' = 1 and A gives a correct guess μ' = μ;otherwise a tuple was given from D_rand when S outputs c' = 0 .

According to [3], the advantage of the simulator to output a correct v ' = v is

Theorem 2: If the CTDH assumption holds in G , G_T ,then the ABPRE scheme has master key security.

Proof: The simulator S receives a tuple

and a challenge index set I * . To output g^abc , the simulator S does as follows:

Init: S chooses α_i ,β_i ,γ_i at random from Z_p for i ∈ N and generates the public key and set Y = e(g,h)^ab = e(g_b ,g₃) . Then it computes public keys as follows:

i ∈ I^* , T_i = g^αi ,T_n+i = g_b^βi ,T_2n+i = g_b^γi ;

i ？ I^* , T_i = g_b^αi ,T_n+i = g^βi ,T_2n+i = g_b^γi ;

S outputs public parameter

Key generation oracle: A makes a query to the key generation oracle with an index set I_q ⊆ N where I_q ≠ I *. An index j must belong to the following conditions ((j ∈ I_q) _∧ (j ？ I *) or (j ？ I_q) _∧ (j ∈ I *) ). For this reason,we just analyze the case of (j ∈ I_q) _∧ (j ？ I *).

For every i ∈N,S chooses r'_i ∈ Z_p at random and implicitly sets r_i in the following ways: r_i = br'_i (i ≠ j ; ), r_j = ab + br'_i (otherwise).

Denote

and

For i ∈ I_q , i ≠ j : if i ∈ I*

else i ？ I*

For i ？ I_q , i ≠ j : if i ∈ I* ,

else i ？ I*

For, i = j : ,

It outputs a secret key

Rekey generation oracle: A makes a query to the key generation oracle with an index set I_q ⊆ N and access structure AS , if I_q ≠ I*. , obtain usk from KGEN(I_q) and generate rk = RKGEN(usk ,AS) ; else I_q = I*.

Select j ∈ I* and

at random for each i ∈ N ￦ {j};

Implicitly set

and

for i ∈ N;

Compute

for i ∈ N :

If i ≠ j, i ∈ I* ,

Else if i ≠ j, i ？ I*

Else if

Output

where C is the ciphertext of g_d · g^t under the access structure AS.

Re-encryption oracle: A makes a query to the key generation oracle with an index set I_q ⊆ N and access structure: if I_q ≠ I *. , obtain rk from RKGEN (usk ,AS') and generate C' = REENC(rk ,C) ; else I_q = I*.

-For i ∈ N :

- +d_i appears in AS,

where

- ？d_i appears in AS ,

where

- Otherwise,

where

It outputs a secret key usk^* for I^* including

If it is a valid secret key, usk^* satisfies the following equation:

The decryption oracle is straightforward, since the secret key and re-key could be correctly generated from the Key generation and Rekey generation oracle.

It outputs

and solves the CTDH problem.

Majority of ABE or ABPRE schemes require computing a number of pairing operations to generate the ciphertext depending on unique attributes but the computational cost of a pairing operation is much higher than other operations. For this reason, a small number of pairing operations is important factor for efficient cryptography algorithms. In 2009, Emura et al. [9] presented a constant length of pairing operations in an ABE scheme. This scheme is the motivation of our algorithm. In our scheme, we propose an expansion algorithm of ABE, ABPRE maintaining a constant pairing operation. A comparison of computation complexity is illustrated in Table 1.

The notation kG and kC_e denote the k-times calculation over group G and pairing, respectively. Let u = {att₁,att₂,...,att_n} be the set of attributes.

Let r₁ and r₂ be a set of attributes associated with the ciphert

ext and a set of attributes associated with the secret key, respectively. Let

be the total number of possible statements of attributes.

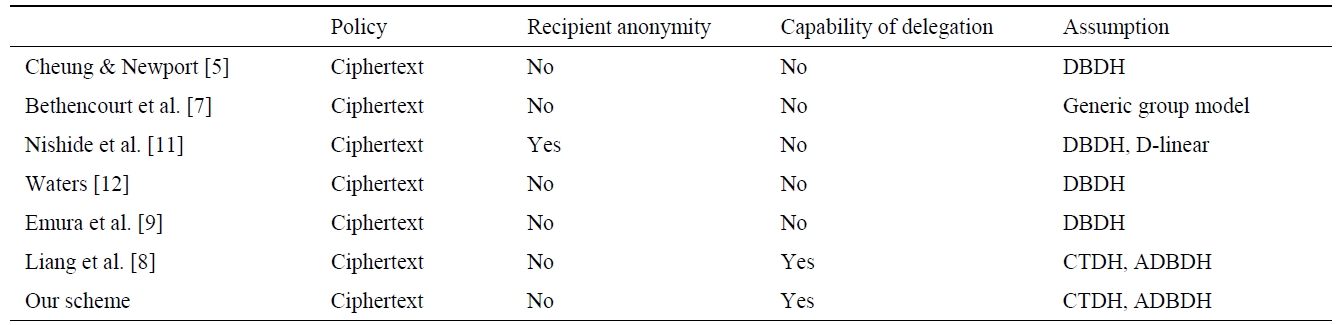
Comparison of some properties including policy anonymity, capability of delegation, and security assumption is illustrated in Table 2. All schemes follow the ciphertext policy. Nishide et al. [11] scheme only provides recipient anonymity. Capability of delegation is a strong feature of ABPRE-based schemes. Therefore, we can empower designated users with the capability of decryption. Our security assumption is based on CTDH and ADBDH. This provides a selective-structure chosen to be plaintext secure and master key secure.

In the paper, we present the ABPRE with constant number of pairing operations. The scheme is motivated from previous CP-ABE by computing constant length and number of pairing operations. Compared to previous ones, our proposal has the strength of its capability of delegation. Through the feature, we can empower designated users to decrypt the ciphertext re-encrypted with a new access structure. The scheme can be adapted to various applications including e-mail forwarding and distributed file systems.

Future work includes how to implement the scheme efficiently in various environments such as traditional computing environments and embedded systems (wireless sensor network, near field communication, and radio frequency identification).