Telematics systems offer a wide range of information for convenient and safe driving. The telematics terminal, once mounted on a car, allows one to observe what transpires inside the car. Telematics emergency rescue services make it possible to track the location of a car in need of emergency rescue, in the event that the car has been turned over, fallen off or deviated from a roadway due to an accident and/or a natural disaster, or in cases where the car is unable to run under its own power due to obstructions on the road or when heavy snowfall traps the occupants inside the vehicle.

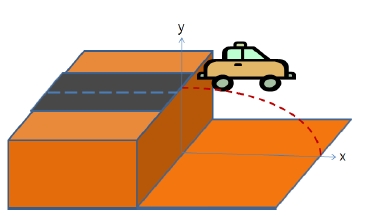
In this paper we measure the distance a car travels as a function of the car’s velocity when it drives over holes in the roadway or drives off the roadway. This could involve sinkholes, that is, depressions with a depth of two, three, and four meters formed on parts of a roadway that were washed away by flooding, or it could involve a car falling disaster resulting from human error such as a failure to stay on the road. Fig. 1 depicts a depression in a road and how a car falls off the roadway. The simulated car was moving at velocities of 50, 60, 70, 80, and 90 m/sec when it went over the edge of the depressions on the roadway. What concerns us here is the horizontal distance the car will travel after it passes the edge of the roadway. If the time the car will be in the air is known, the horizontal distance can easily be calculated. Fig. 2 shows actual cars falling off roads.

What follows is a brief description of studies based on uniformly accelerated motion. One study was conducted using a method whereby the exact value of the field equation, which represents a magnetic monopole in a state of uniformly accelerated motion, is found by applying equiangular transformation to the well-known value of the magnetic monopole [1]. Another study was conducted to develop materials for learning the key ideas of calculus; this study involved the analysis of the changes in the graph in which the state of uniformly accelerated motion is modeled [2]. According to the national design standards for highway acceleration lanes, if a car enters the acceleration lane from the ramp at a velocity of V₁, then runs along the acceleration lane at a constant acceleration (or uniformly accelerated motion) of a, and finally enters the main lane at a velocity of V₂, the length of the acceleration lane (L), which depends on the difference between V₁ and V₂, is calculated as described as [3]

where V₁ is the velocity at which the car approaches the acceleration lane from the ramp, V₂ is the velocity at which the car approaches the main line from the acceleration lane, and a is the acceleration at which the car runs along the acceleration lane.

Meanwhile, several studies have addressed projectile motion. One study involves a physical examination of the act of men urinating. According to this study, the urine excreted by men while urinating was found to take a parabolic path followed by a projectile due to the acceleration of gravity [4]. In addition, 3D game programming and mathematics for computer graphics applications deal with projectile motion that follows the fundamentals of linear physics [5]. Web-based video digitizing systems are also used to do research into projectile motion [6]. According to a study on the orbit matching of the motion of video objects, spatial distance is used to distinguish small projectile motion made by strollers or joggers from the large projectile motion made by high jumpers who jump up and over a bar [7].

Like a moving car, an object with varying speeds is said to gain acceleration. Quantitatively, velocity is defined as the ratio of change in location. Likewise, acceleration can be defined as the ratio of change in velocity. The average acceleration at the time interval Δt is as

where Δv refers to the change of velocity over time, and

means the average acceleration. The instantaneous velocity, the amount of velocity that can vary with time at each point in time, refers to the limit of the ratio between the displacements Δx and Δt as the time interval Δt approaches zero(0). The velocity is as in

Thus, the instant velocity a is as in

Uniformly accelerated motion means motion with constant acceleration. If an object starts to move at a velocity of v₀ at an initial point in time t = 0, and moves at a velocity of v at a later point in time t, the change in velocity divided by the time interval between t = 0 and t is the average acceleration

Since acceleration is constant, however, the average value of acceleration is the same as the instantaneous value. The acceleration is as in

Eq. (3) can be restated as shown in (5):

The change in velocity, in other words, is the product of the initial velocity and time.

As described above, in the case of constant acceleration,we find the velocity as a function of time. Now, displacements over time should be addressed. Unless the velocity is constant, there is no way of multiplying the velocity by time. In case of constant acceleration, however, the velocity increases at a constant rate, and the average velocity at a certain time interval becomes the average velocity between the initial point in time and the end point in time of that time interval. Eq. (6) is the average velocity between the initial point in time t = 0 and the end point in time when the velocity is v.

The average velocity can be found by dividing the displacement by the time interval. If t = 0 and an object is at a certain location x₀, the average velocity between two points in time 0 and t is as

In Eq. (7), x refers to the location of the object at the point in time t. If

in (7) is the same as

in (6), the location of the object is as in

The instantaneous velocity v is already derived as in (5). What follows is a combination of (5) and (8) that results in the location as a function of time

It has been determined that the only force acting upon an object in free fall is gravity. Such an object experiences a downward acceleration of 9.8 m/sec², the value of acceleration due to gravity on earth. This acceleration applies to the object upon which the only force acting is gravity. The same acceleration of 9.8 m/sec² applies to all objects near the surface of the earth, regardless of their mass or geometrical properties. The symbol g stands for gravitational acceleration.

The gravitational acceleration 9.8 m/sec² is constant acceleration near the surface of the earth. This means the velocity of an object falling vertically changes at a velocity of 9.8 m/sec. In other words, when an object is moving upwards, it moves slowly until it stops to change its direction. On the other hand, when it is moving downwards, the velocity increases. If you take the upward direction as positive, acceleration a will be -g.

The motion of a projectile which is in a state of both horizontal and vertical motion refers to the motion wherein the projectile experiences a vertical acceleration and the downward direction thus experiences a change in velocity. Generally, a projectile is thrown sideways into the air. If the velocity is divided by vertical and horizontal directions, no force will act on the horizontal direction, making the projectile move at a constant velocity. In contrast, the gravitational acceleration will act on the vertical direction, making the projectile move more slowly until it changes its direction and falls. In this case, the velocity continues to increase in the negative (downward) direction. To deal with projectile motion, we will neglect any changes in the direction and size of gravitational acceleration, to say nothing of air resistance.

To describe projectile motion, it is necessary to have the coordinate system with the x axis horizontal to the initial velocity of a projectile, and the y axis vertical with the positive direction going upwards. In this configuration, the direction toward the z axis has no components of velocity and/or acceleration; this allows for two dimensional motions in the xy plane. For the gravitational acceleration, a_x is 0 while a_y is -g. Therefore, Eqs. (5) and (9) can be expressed as follows, from (10) to (13):

As described above, g has a negative sign for acceleration pointing downwards.

Our simulation program was performed using Visual C++ running on Microsoft Windows XP. The simulations included determining the time and distance it took for the car to fall vertically. To deal with projectile motion, we assumed that any changes in the direction and size of gravitational acceleration as well as air resistance were negligible.

Analyzing vertical motion allows one to determine the above-mentioned time. The reason for vy_o = 0 is that the car went off the road in a horizontal motion. If the origin of the coordinate system is placed under the bottom of the washed-out road, y₀ becomes 2, 3, and 4 m, respectively. First off, if y = 0, t is obtained as

The equation above shows how long it took the car to fall straight down to the bottom of the washed-out road from a height of 2, 3, and 4 m. Eq. (15) is the distance the car traveled horizontally during that time at a velocity of 40, 50, 60, 70, and 80 m/sec.

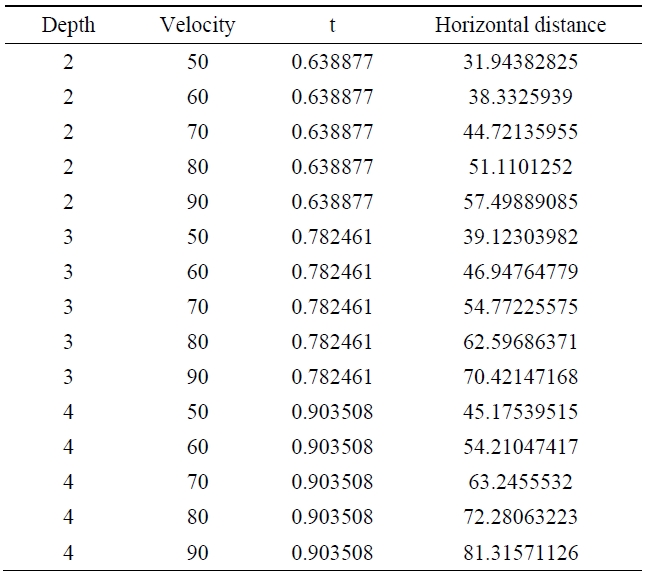
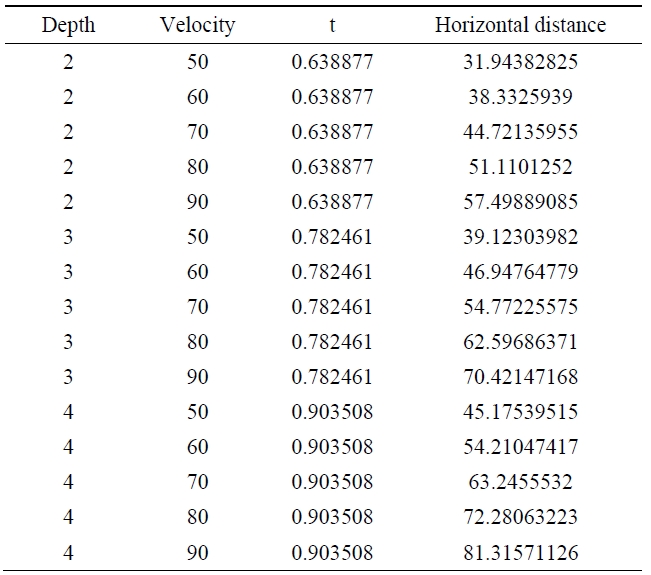
Table 1 shows how far the car, while running at a velocity of 50, 60, 70, 80, and 90 m/sec will be thrown into the air from the end of the washed-out roadway with depressions 2, 3, and 4 m deep before it falls down to the ground. t refers to the time it took for the car to fall free, and x to the distance it traveled horizontally.

Here, g is the acceleration due to gravity that acts on an object, making it move downwards, regardless of whether it is in upward, downward, or horizontal motion. It is the gravitational constant 9.8 m/sec² that makes the object's velocity change at 9.8 m/sec per second.

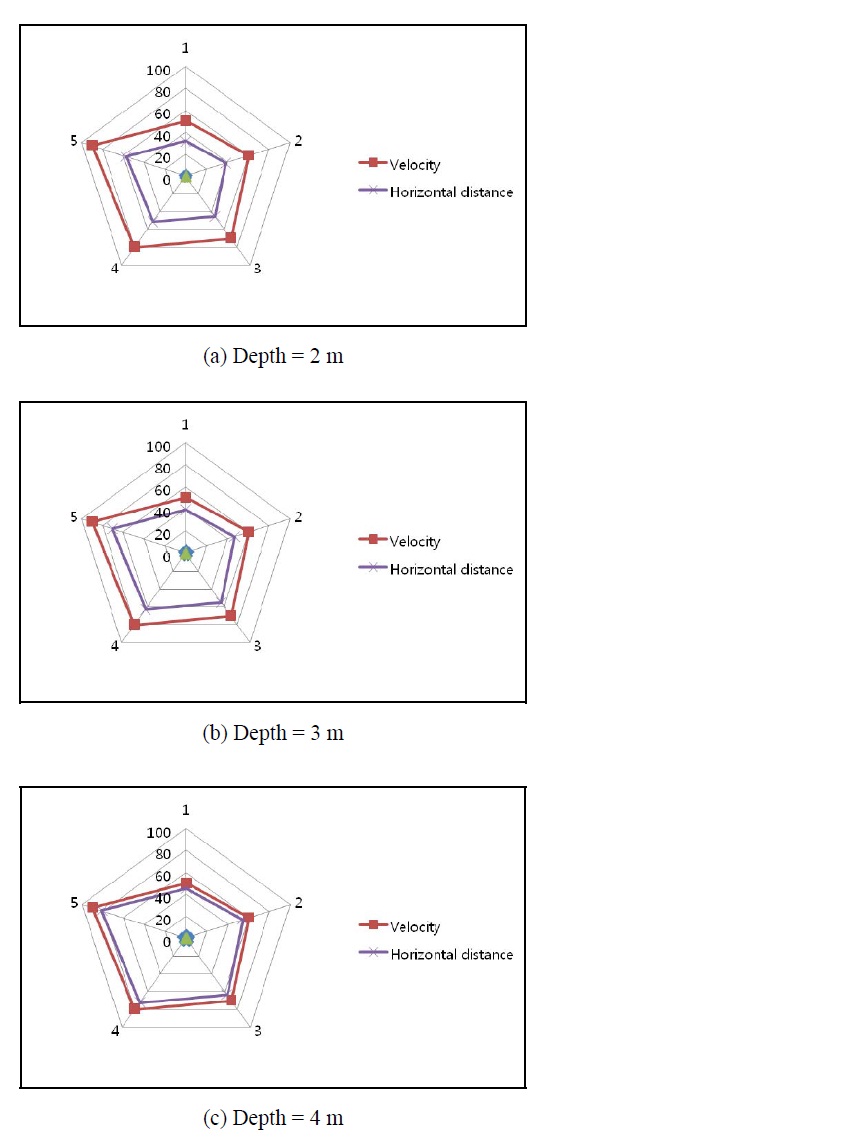
Fig. 3 is a graphical representation of this process. For the section of the two-meter-deep washed-away roadway, the value of t is constant, which indicates the velocity and horizontal distance. The footage in Fig. 4 shows those trapped inside a wrecked car being rescued after the car went off the roadway and fell to the ground.

Automotive safety and accident response time is very important in telematics. In particular, very often the unintended accident and accordingly a response to it is urgently needed. This paper provided a detailed description of how far a car would be thrown from the end of the depressions on a roadway until it reached the ground. We assumed that the car accident was due to either a natural disaster such as a flood or human error such as falling off an overpass. On the assumption that any changes in the direction and size of gravitational acceleration as well as air resistance are negligible, we showed the maximum free-fall time, velocity, and horizontal distance the car traveled through a graphical representation of our simulation results.This study illustrates to the telematics industry the potentially catastrophic dangers associated with car accidents due to falling off roadways and it is hoped that some of these accidents can be prevented in the future.