In this paper, we compare the accuracy of most representative radio frequency identification (RFID) tag estimation functions in the context of minimizing RFID tag identification delay. Before the comparisons, we first evaluate the accuracy of Schoute's estimation function, which has been widely adopted in many RFID tag identification processes, and show that its accuracy actually depends on the number of tags to be identified and frame size L used for dynamic frame slotted Aloha cycles. Through computer simulations, we show how the accuracy of estimation functions is related to the actual tag read performance in terms of identification delay.
Due to the ability to identify objects wirelessly without line-of-sight, radio frequency identification (RFID) systems are becoming noticeably prevalent. RFID systems are rated to be particularly attractive for applications such as retail, inventory management, and supply-chain management [1, 2].
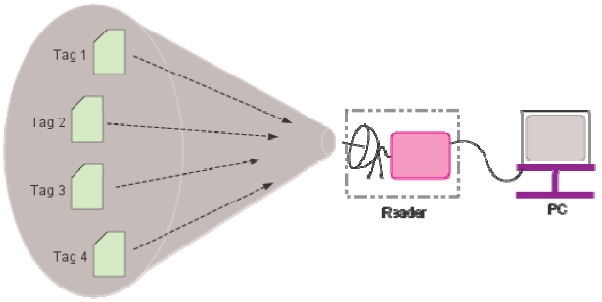
RFID systems consist of a reader and multiple tags. While the reader is powerful in terms of memory and computational resources, there are many types of tags that differ in their computational capabilities. Among various tag types, passive ones are becoming more and more popular for large scale deployments due to their low cost [2].
Collision due to simultaneous tag responses is one of the key issues in RFID systems. It results in wastage of bandwidth and energy, and increases identification delays. To minimize collisions, RFID readers must use an anti-collision protocol. The design of anti-collision protocols becomes more challenging considering that the tags must be simple, cheap, and small enough [3].
Among various RFID anti-collision protocols, dynamic frame slotted Aloha (DFSA) based anti-collision protocols are most commonly used for passive RFID tag identification processes, and hence our focus is mainly directed toward DFSA. Such protocols have the ability to adjust their frame size in accordance with varying tag populations using a tag estimation function.
Consider an RFID system adopting DFSA as an anti-collision protocol and suppose there exist
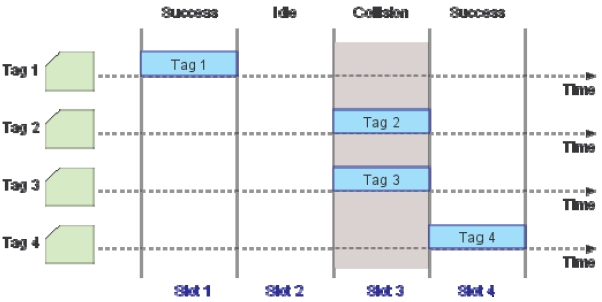
The overall tag reading procedures with DFSA [3-5] can be outlined as follows: Initially, the reader starts the read process with a preset frame size. During DFSA frames, each tag chooses a slot randomly to transmit its identification. The reader then monitors the status of each slot and counts the number of slots filled with zero, one, or multiple tag responses. This observation is then translated to a tag estimate
It is noteworthy that an inaccurate tag estimate can result in non-optimal frame sizes and incorrect values of
The most well-known tag estimation functions proposed so far are Schoute's estimation function [6] and Vogt's estimation function [4, 5]. Several authors, such as Zhen et al. [3] and Cha and Kim [7], have adopted Schoute's estimation function for their RFID tag identification schemes. More specifically, [3] also proposed to set the optimal frame size according to 1.4×
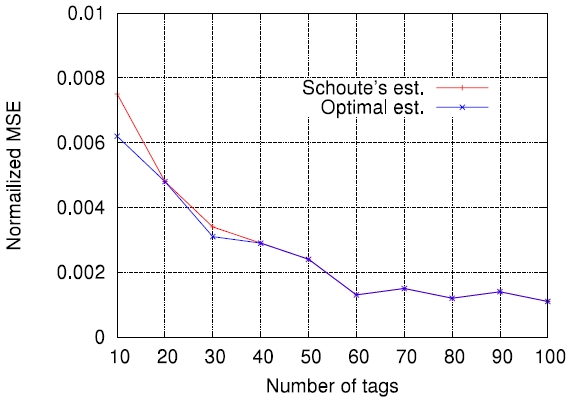
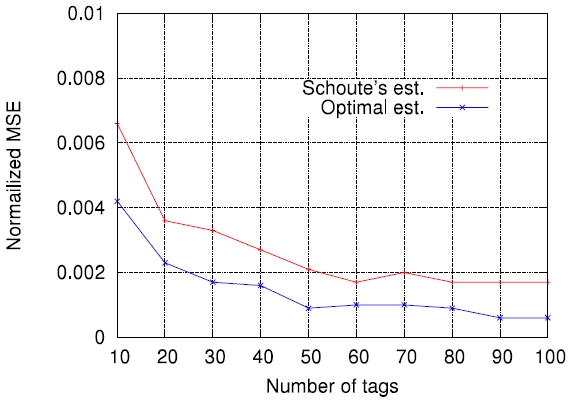
In this paper, we compare the accuracy of several representative estimation functions in the context of minimizing the RFID tag identification delay. Before the comparisons, we evaluate the accuracy of Schoute's estimation function [6], which has been widely adopted in many cases, and show that its accuracy depends on the number of tags to be identified and frame size used for DFSA cycles. To date, this work is new. Finally, through computer simulations, we show how the accuracy of estimation functions is related to the actual tag read performance in terms of identification delay.
The remainder of this paper is organized as follows: In the next section, we describe the optimal design problem for RFID systems. In section III, we introduce most representative estimation functions. Section IV first discuss on the accuracy of Schoute's estimation function [6] and then compares the accuracy of the estimation functions described in Section III. section VI concludes the paper.
II. OPTIMAL DESIGN PROBLEM FOR RFID SYSTEMS
We consider RFID systems adopting passive tags and DFSA with no muting as the anti-collision protocol [2]. By DFSA with no muting, it is meant that no tags are informed of the outcome of each reading cycle from the reader. Similar to basic frame slotted Aloha (BFSA), DFSA operates in multiple cycles but with the key difference that in each read cycle, the reader uses a tag estimation function to vary its frame size. A tag estimation function calculates the number of tags based on the information collected through each reading frame, consisting of the number of idle slots (
With the DFSA protocol in operation, the frame size
The optimal design problem for the tag reading process can be established as follows: Given an assurance level α, for
Suppose there are
In this section, we first survey some past representative works on devising proper tag estimation functions and optimal frame sizes and discuss some problems associated with these studies. As a preliminary step, we are interested in the lower bound of the number of tags in the interrogation zone upon observing O
Schoute's estimate [6] can be obtained based on the assumption that with
Schoute's estimate has been adopted in many schemes, including [3, 7].
With
is given by
Based on the observations until the
where for a function of
denotes the average number of slots with occupancy greater than or equal to 2. Thus it always holds that
It is noteworthy that Vogt's estimate utilizes only the last observation O
>
B. Kim and Park's Estimate
In DFSA, the tag estimate
and it holds that
For the sake of brevity we denote the common frame size of all the read cycles in the
We can take sample averages after each read cycle in the
Kim and Park’s estimate
for the
With
P[X = k | X ≥ 2] = P[X = k]/P[X ≥ 2], k = 2,3,...
where
Therefore, the average number of tags in the slot on the condition that the slot is in collision, denoted by
If we always adjust the frame size
Table 1 shows the values of
and thus for large
[Table 1.] Computed values of E[X | X ≥ 2]
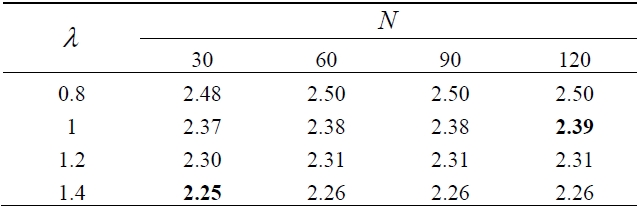
Computed values of E[X | X ≥ 2]
Schoute's estimate [6] can be obtained based on the assumption that with
where
For each tag set size
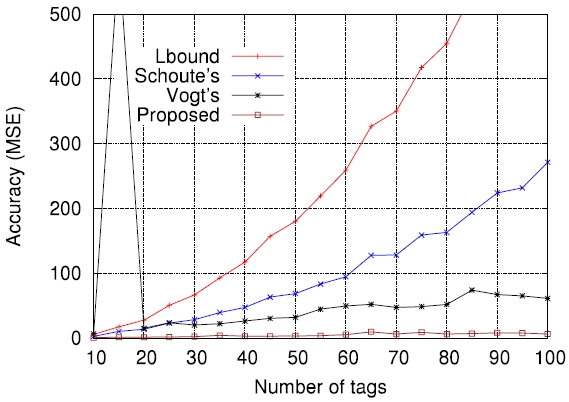
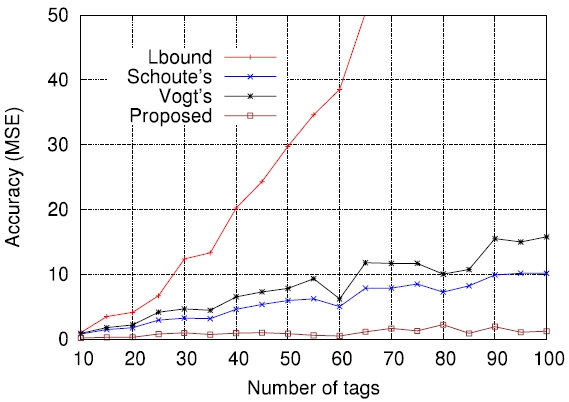
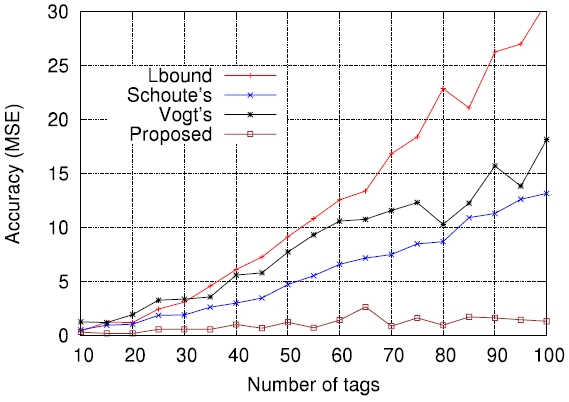
On the other hand, Figs. 5-7 compare the performance of the four estimation functions described in section III, namely the lower bound, those of Schoute [6], Vogt [4, 5], and Kim and Park [8], in terms of the MSE, which is defined by
Figs. 5-7 are the comparison results for
[Fig. 5.] Comparisons of four estimation functions for λ = 0.5 in terms of mean squared error (MSE).
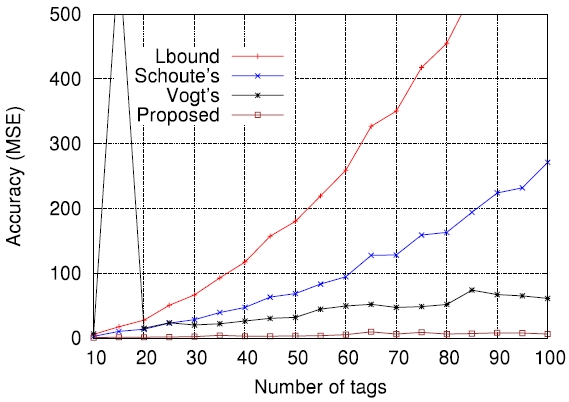
[Fig. 7.] Comparisons of four estimation functions for λ = 1.5 in terms of mean squared error (MSE).
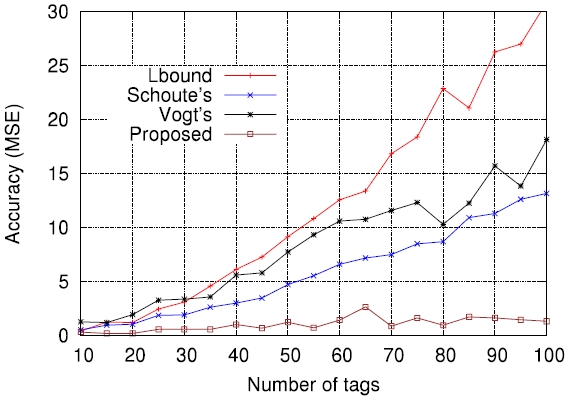
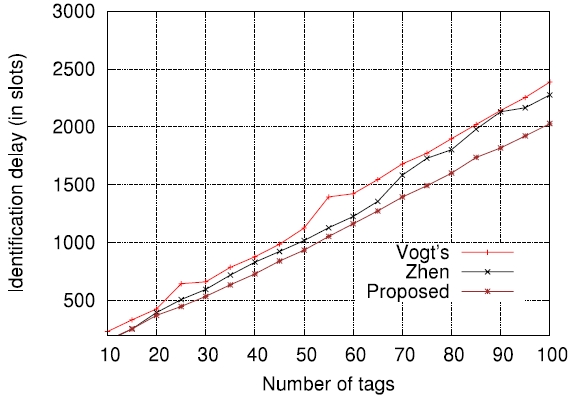
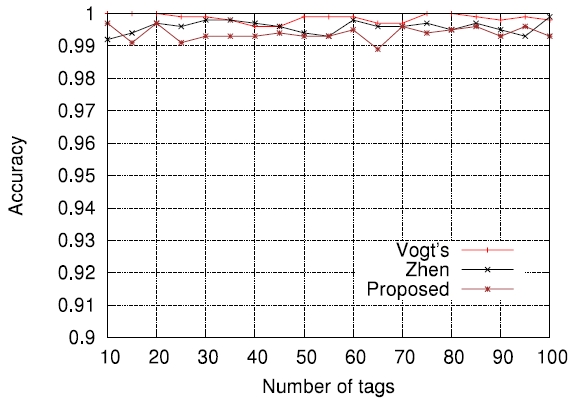
In order to further evaluate how the accuracy of estimation functions is related to the actual tag read performance in terms of identification delay, we applied those to actual passive tag identification processes and performed computer simulations (the lower bound has been excluded on purpose). The assurance level aspired to, α , was set to 0.99 , that is, the requirement was that on average, the number of cases failing to identify all tags should not exceed 1% of all identification processes. The tag set size
In this paper, we compared the accuracy of several representative estimation functions in the context of minimizing the RFID tag identification delay. Before the comparisons, we first evaluated the accuracy of Schoute's estimation function [6] which has been widely adopted in many cases and showed that its accuracy indeed depends on the number of tags to be identified and frame size used for DFSA cycles. Through computer simulations, we also showed how the accuracy of estimation functions is related to the actual tag read performance in terms of identification delay.
![Computed values of E[X | X ≥ 2]](http://oak.go.kr/repository/journal/11026/E1ICAW_2012_v10n1_33_t001.jpg)