In the linearly constrained adaptive array [1], the desired signal is estimated such that the array weights are updated iteratively by the linearly constrained least mean square (LMS) adaptive algorithm. It has been shown that the algorithm performs well if the desired signal and the interference signals are uncorrelated. It was shown that the signal interaction inherent in the algorithm causes partial cancellation of the desired signal in the array output even though the desired signal and the interference signals are uncorrelated [2]. If the interference signals are correlated with the desired signal, the signal interaction causes the desired signal to be partially or totally cancelled in the array output depending on the extent of correlation between the desired signal and the interference patterns.

To avoid the signal cancellation phenomenon, a variety of methods [2-9] have been proposed, such as a master-slave type array processor [2], a spatial smoothing approach [3], and an alternate mainbeam nulling method [4, 5].

In this paper, a novel approach to the general linearly constrained adaptive array [1] is presented to improve the nulling performance of the conventional linearly constrained adaptive arrays in coherent and noncoherent environments. The desired response is formed as the output of the conventional beamformer weighted by a gain factor. The input signals to the conventional beamformer are given by those to the adaptive array. The narrowband and broadband adaptive arrays are implemented with coherent and noncoherent interference patterns.

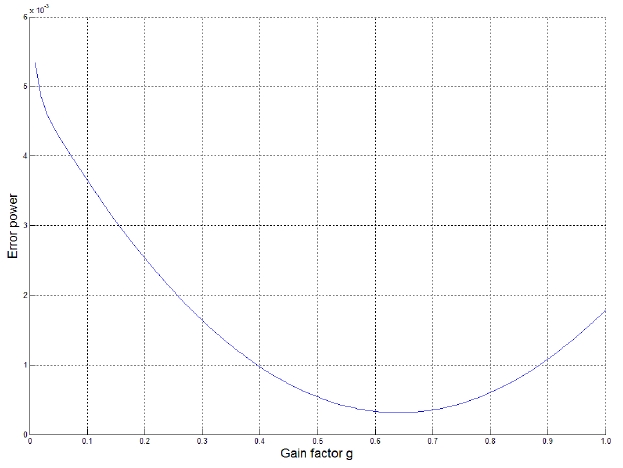
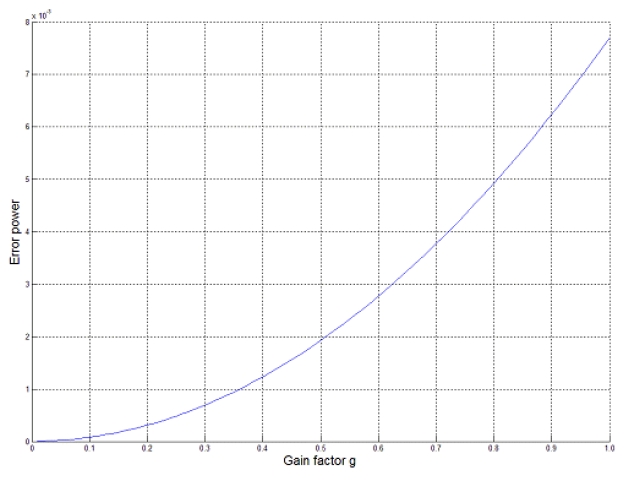
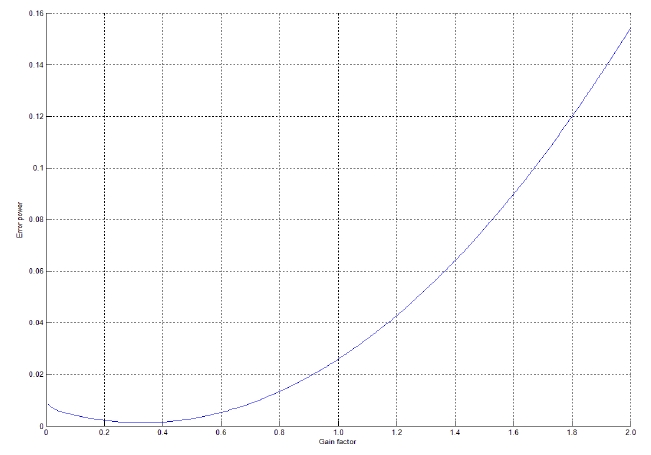
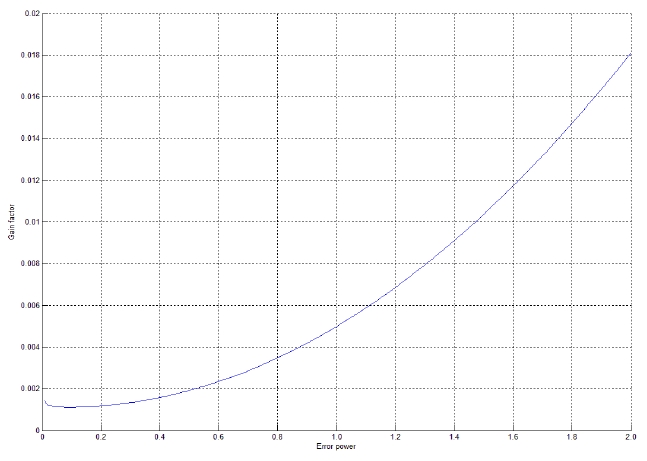
The nulling performance is shown to depend on the value of the gain factor such that there exists an optimal value of the gain factor that minimizes the error power between the array output and the desired signal.

The proposed approach may be applied to the multipath environment in the area of wireless communications.

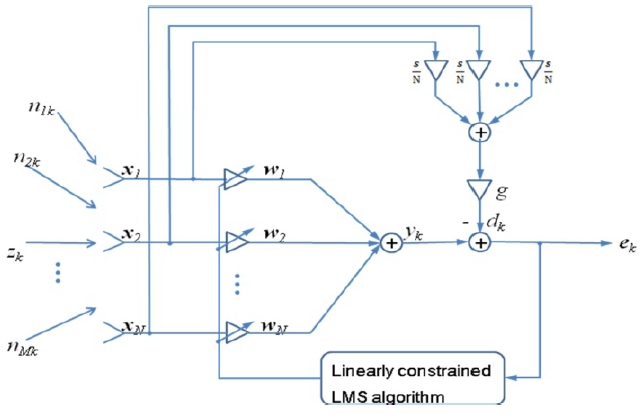
The general linearly constrained narrowband adaptive array with Q sensor elements is shown in Fig. 1. The weights , w_n, 1 ≤ n ≤ N, are updated iteratively to minimize the power of the error output with a unit gain constraint in the look direction (i.e., the direction of the desired signal).

The optimization problem of finding an optimum weight vector for estimation of the desired signal is formulated as

where the weight vector w, and the steering vector s of the desired signal are given by

where β is the radian frequency of the desired signal, τ_o = d sin θ_o/ u, θ _o is the angle of incidene from the array normal, d is inter-element spacing, υ is the signal propagation velocity, k is an iteration index, and E and T denote expectation and transpose, respectively.

The error signal is given by

where the y_k is given by

and the desired response d_k is

g is a gain factor for the desired response, and H denotes the complex conjugate transpose. It is assumed that the angle of incidence for the desired signal is known a priori.

The iterative solution for the optimum weight vector may be found by the method of Lagrange multipliers [1], or what is called the general linearly constrained LMS algorithm,which is given by

Where

μ is convergence parameter, I is the N × N identity matrix,and * denotes complex conjugate.

The weight vector w_k is updated iteratively to find a suboptimal solution of the optimization problem in (1). It is shown that the suboptimal solution depends on the gain factor g in the desired response path in Fig. 1.

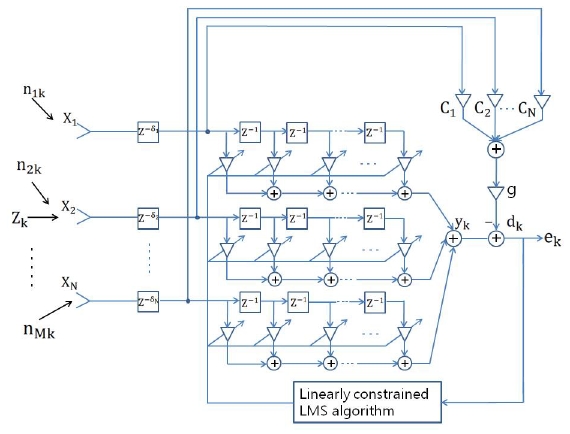
A linearly constrained broadband adaptive array is shown to cancel out the desired signal in a coherent environment[2]. To prevent the signal cancellation phenomenon, a general linearly constrained broadband adaptive array is proposed. The general linearly constrained broadband adaptive array with N sensor elements followed by L taps per element is shown in Fig. 2.

The desired response d_k is produced as the output of the conventional beamformer scaled by the gain factor g.

To minimize the mean square error output with a unit gain constrained in the look direction, the weights are adjusted iteratively by the general linearly constrained LMS algorithm [1] as follows.

where C is an NL × L constraint matrix, F is given by

f is an L × 1 constraint vector, P is a projection matrix that projects any vector onto the constraint subspace and is given by

It is worth noting that the constraint subspace is the orthogonal complement of the column space of C.

The array weights are updated such that the desired signal is estimated in a least mean square sense such that the array output power is minimized while maintaining the unit gain in the look direction.

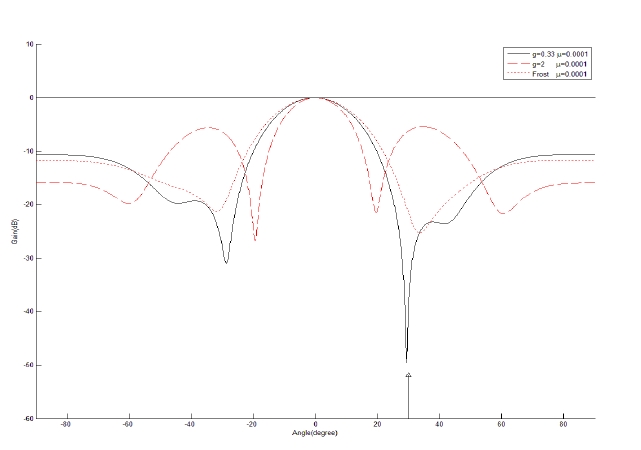
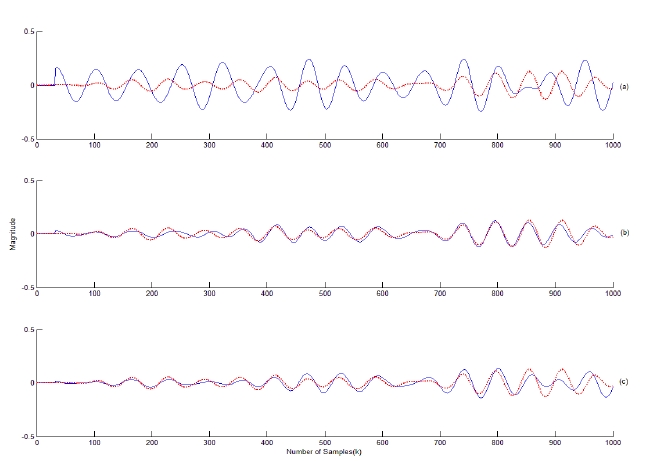
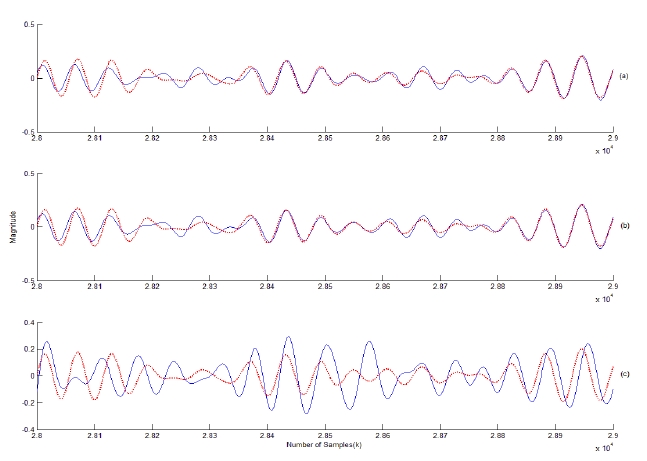
A narrowband linear array with 7 equispaced sensor elements is employed to examine the performance of the proposed method. The desired signal is assumed to be a sinusoid incident at the array normal. The cases for one and two coherent signal, and one noncoherent signal interference are simulated. The frequency of the noncoherent interferencen is assumed to be half that of the desired signal in the noncoherent case. The incoming signals are assumed to be plane waves. The nulling performances are compared with respect to the gain factor g and the conventional linearly constrained adaptive array proposed by Frost [1]. The convergence parameter μ is assumed to be 0.001.

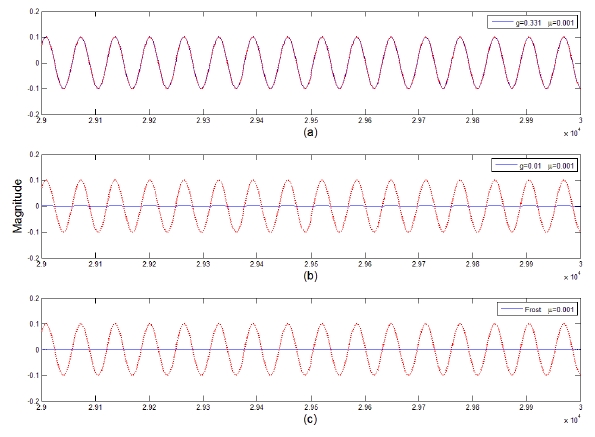
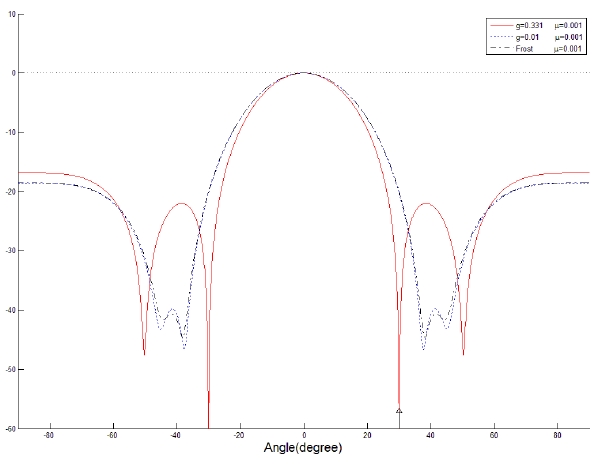
1) One Coherent Signal Interference Case

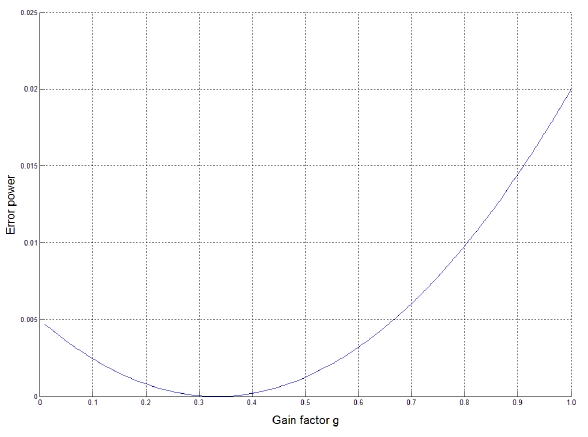
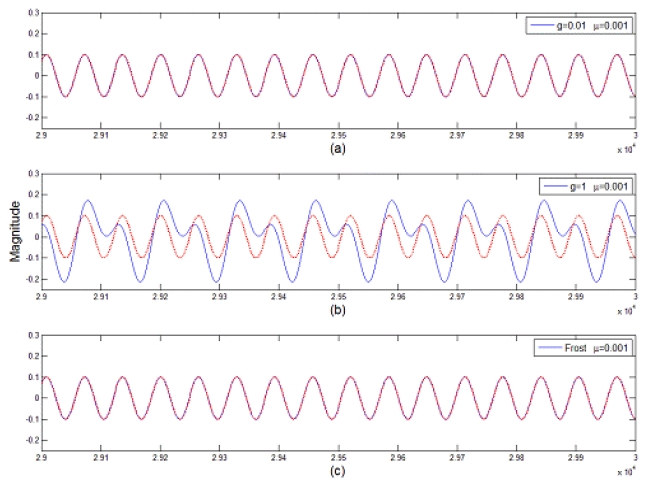
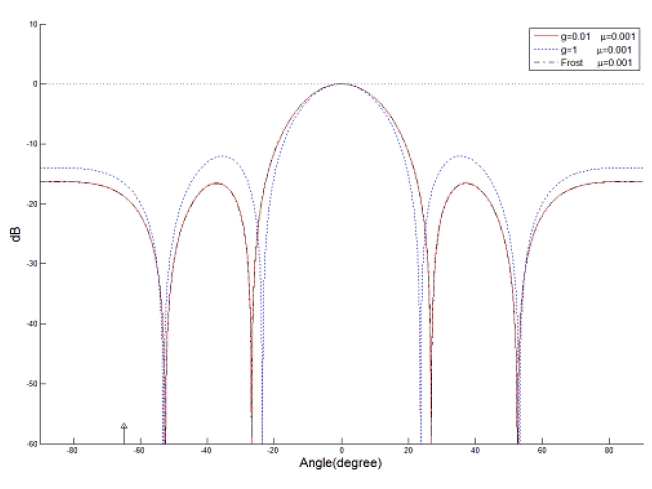
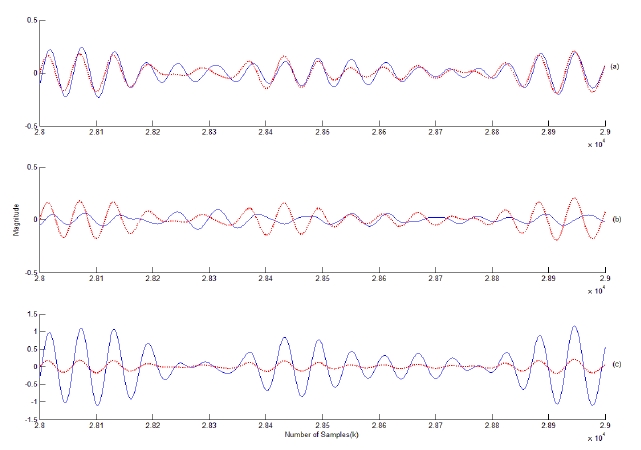
It is assumed that a coherent interference is incident at 30° from the array normal. The variation of the error power between the array output and the desired signal is displayed in terms of the gain factor g in Fig. 3. The optimum value of g that yields the minimum error power is shown to be 0.331. The comparison of the array performance for g = 0.331, 0.01,and the conventional linearly constrained adaptive array proposed by Frost [1] are shown in Figs. 4 and 5 with respect to the array output and the desired signal for k = 1-1,000 and 29,001-30,000 samples, respectively. It is demonstrated that the case for g = 0.031 performs best while the case for g = 0.01 performs better than Frost’s. It is shown that the desired signal of Frost’s array disappears (i.e., is cancelled out) in the steady state array output for 29,001 ≤ k ≤ 30,000.The beam patterns are shown in Fig. 6, in which the case for g = 0.031 makes a deep null (-51 dB) in the direction of the interference pattern (30° ).

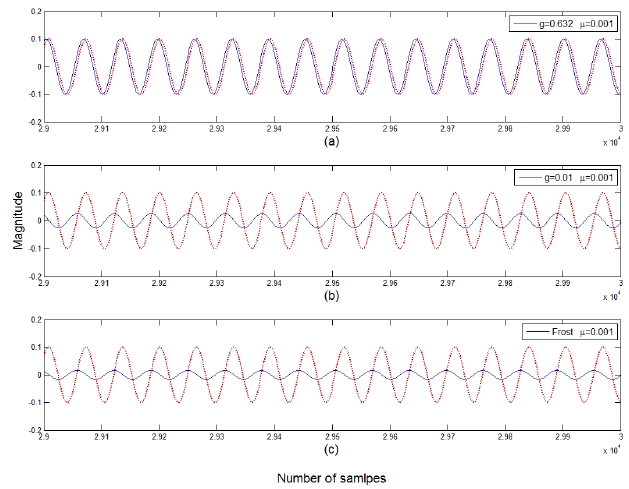
2) Two Coherent Signal Interference Case

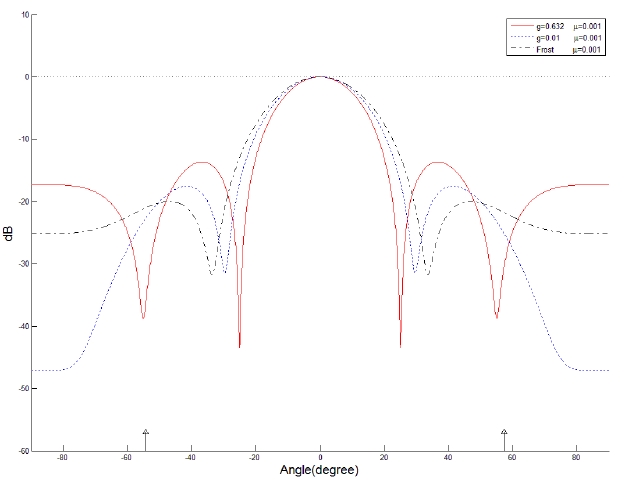
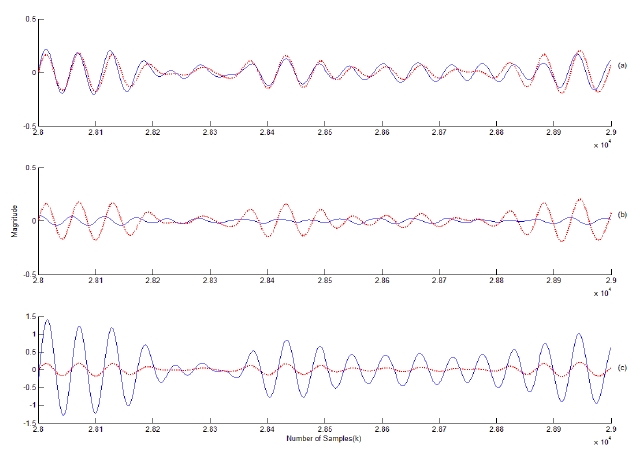
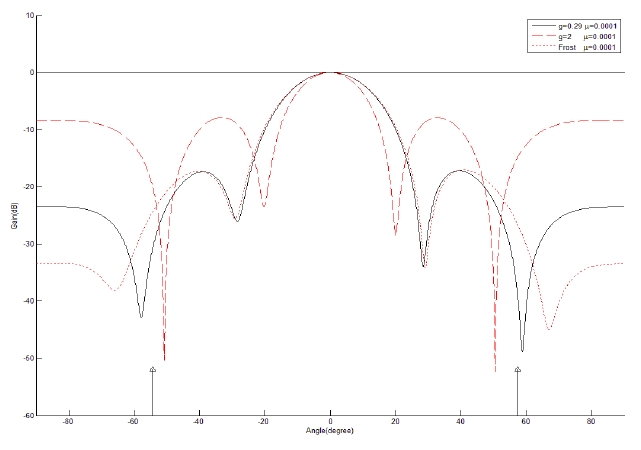
It is assumed that two coherent signal interferences are incident at -54.3° and 57.5° from the array normal. The variation in the error power between the array output and the desired signal is displayed in Fig. 7. The optimum value of g is shown to be 0.632. The comparison of the array performances for g = 0.632, 0.01, and the conventional linearly constrained adaptive array proposed by Frost are shown in Figs. 8 and 9 with respect to the array output and the desired signal for k = 1-1,000 and 29,001-30,000 samples, respectively. It is shown that the case for g = 0.632 performs best while the case for g = 0.01 performs similarly to Frost’s. The beam patterns are shown in Fig. 10, in which the case for g = 0.632 makes two deep nulls (-36.6 dB and -30.4 dB) at two incident angles (-54.3° and 57.5° ) of the coherent interference patterns while the gains for Frost’s are -21.0 dB and -21.8 dB and the gains for g = 0.01 are -22.7 dB and -25.1 dB, respectively.

3) One Noncoherent Signal Interference Case

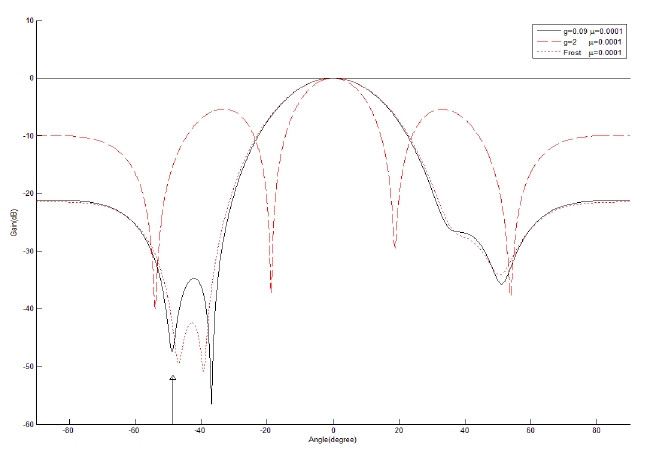
It is assummed that a noncoherent interference is incident at -64.9° from the array normal. The variation of the error power between the array output and the desired signal is displayed in Fig. 11. The optimum value of g is shown to be 0.0. The comparison of the array performance for g = 0.01, 1.0, and the conventional linearly constrained adaptive array proposed by Frost are shown in Figs. 12 and 13 with respect to the array output and the desired signal for k = 1-1,000 and 29,001-30,000 samples, respectively. It is shown that the case for g = 0.01 and Frost’s array[1] yield similar performances while both of them perform better than the case for g = 1.0. The beam patterns are shown in Fig. 14, in which the case for g = 0.01 and Frost’s array yield similar gains (-18.6 dB) at the angle of incidence of the interference.

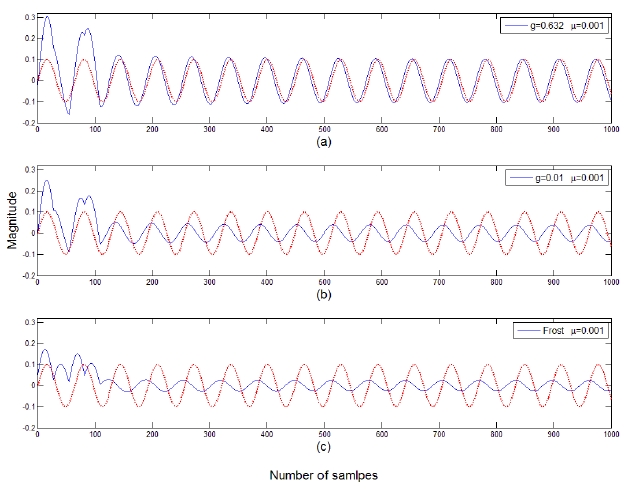
A broadband linear adaptive array with 5 sensor elements and 3 weights per element is simulated with incoming broadband signals. The broadband desired signal is generated by passing a white Gaussian random signal through a 4th-order Butterworth filter such that the bandwidth is 3 Hz with the upper and lower frequencies 8 Hz and 11 Hz, respectively. The incoming signals are assumed to be plane waves. The cases for one and two coherent signal and one noncoherent signal interferences are simulated. The sampling frequency is 608 Hz. The convergence parameter is assumed to be 0.0001.

1) One Coherent Interference Case

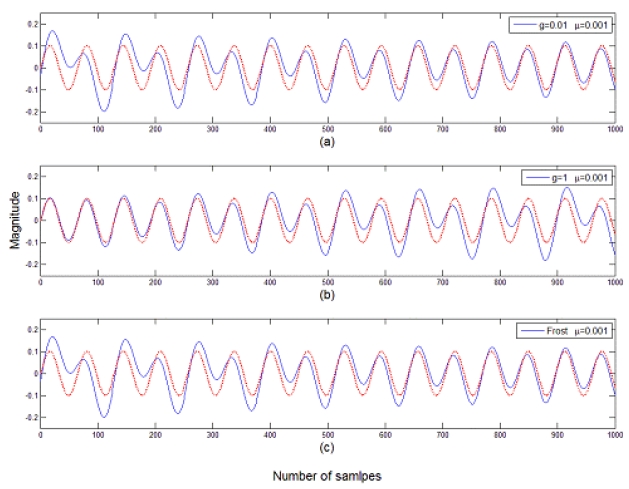
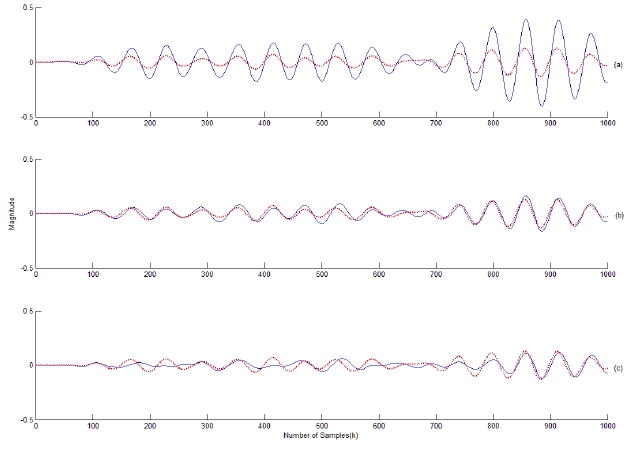
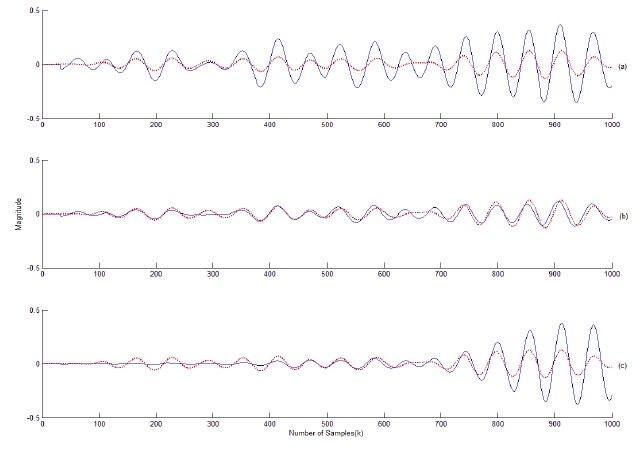
It is assummed that a coherent interference is incident at 30° from the array normal. The variation of the error power between the array output and the desired signal is displayed in Fig. 15. The optimum value of g is shown to be 0.33. The comparison of the array performance for g = 0.33, the conventional linearly constrained adaptive array proposed by Frost and g = 2.0 are shown in Figs. 16 and 17 with respect to the array output and the desired signal for the k = 1-1,000 and 29,001-30,000 samples, respectively. It is shown that the case for g = 0.33 performs best while Frost’s performs better than the case for g = 2.0. The beam patterns are shown in Fig. 18, in which the case for g = 0.33 makes a deep null close to the interference direction.

2) Two Coherent Interference Case

It is assummed that two coherent signal interference patterns are incident at -54.3° and 57.5° from the array normal. The variation in the error power between the array output and the desired signal is displayed in Fig. 19.The optimum value of g is shown to be 0.29. The comparison of the array performance for g = 0.29, the conventional linearly constrained adaptive array proposed by Frost, and g = 2.0 are shown in Figs. 20 and 21 with respect to the array output and the desired signal for the k = 1-1,000 and 29,001-30,000 samples,respectively. It is shown that the case for g = 0.29 performs best while Frost’s performs better than the case for g = 0.01. The beam patterns are shown in Fig. 22, in which the case for g = 0.29 makes two deep nulls around the two incident angles -54.3° and 57.5° of the coherent interferences.

3) One Noncoherent Interference Case

It is assumed that a noncoherent interference is incident at -48.5° from the array normal. The variation of the error power between the array output and the desired signal is displayed in Fig. 23. The optimum value of g is shown to be 0.09. The comparison of the array performance for g = 0.09, the conventional linearly constrained adaptive array proposed by Frost, and g = 2.0 are shown in Figs. 24 and 25 with respect to the array output and the desired signal for the k = 1-1,000 and 29,001-30,000 samples, respectively.It is shown that the case for g = 0.09 and Frost’s array perform similarly, while both of them perform better than the case for g = 2.0. The beam patterns are shown in Fig. 26, in which the case for g = 0.09 and Frost’s array yield a similar gain at the angle of incidene of the interference.

A general linearly constrained adaptive array is proposed and implemented to examine its performance in coherent and noncoherent signal environments. The performance of the proposed approach is examined with narrowband and broadband adaptive arrays in different signal environments.

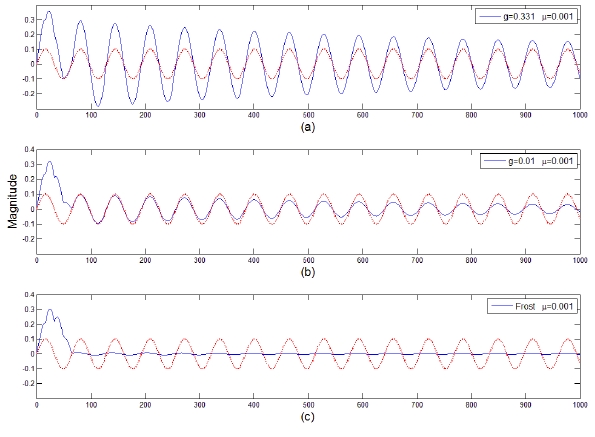
In the narrowband case, it is shown that the proposed approach performs best at an optimal gain factor in a coherent environment while it performs similarly to Frost’s array as the gain factor decreases in a noncoherent environment. In the broadband case, the proposed approach performs better at the optimal gain factor than does Frost’s array in a coherent environment while it yields a similar performance to Frost’s in a noncoherent environment.