With the continuous scaling down of device technology and complicated integration of multi-layered integrated circuits (ICs),planarization at each level of inter-layer dielectric becomes more significant in the current system IC manufacturing. The level of complexity for system IC integration, such as microprocessors and digital signal processors, in general, is more complex than that of memory devices. Planarization was not a required process step in IC fabrication in the era of mid-size integration,which may contain less than hundreds thousands of devices.However, the requirement for the planar surface to improve the depth of focus and photo-patterning resolution in multi-levels of IC integration requires each level of the surface to be a plane.This becomes a critical step in terms of process integration [1].
Numerous methods have been developed for the planarization of the wafer surface. These methods include doped glass reflow,hydrophobicity, spin etch planarization, spin on deposition(SOD), reactive ion etch etch-back, SOD etch back, and chemical mechanical polishing (CMP) [2]. CMP is a widely used planarization method for global planarization in the semiconductor industry, because it is compatible with various materials from dielectrics and metals. It is also useful for planarization of multimaterial surfaces and reduction of severe topography.
Although CMP, compared to other suggested planarization methods, provides usefulness and increased manufacturing
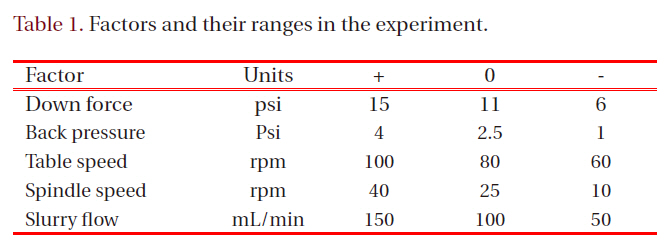
[Table 1.] Factors and their ranges in the experiment.
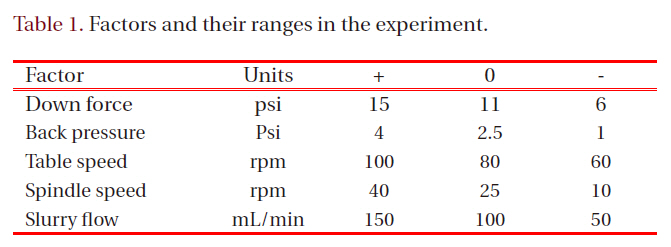
Factors and their ranges in the experiment.
throughput, the process control of the process becomes complex with the increased device integration density and the introduction of newer materials that significantly narrow process latitude with the development of device fabrication technology.Controlling the process parameters cannot be over-emphasized to achieve certain levels of process yield. The large number of tools or process parameters can be grouped into three of the following:1) tool operating related, such as pressure, velocity, and temperature; 2) slurry related, such as abrasive, slurry, and fluid;and 3) pad related.
Separate consideration of each group of parameters for the analysis of the process may not justifiable since they, with respect to the results or outputs of interests, are not independent, but correlated and interact with each other to some degree. In this paper, we have employed statistical design of experiment (DOE)to investigate statistical inference of the individual parameters and their interactions for the figure of merit of the CMP process,removal rate (RR) and uniformity. A series of CMP experiments was followed by the DOE, employing a fractional factorial design with five process parameters. The measured wafer metrology was statistically modeled and analyzed to draw objective conclusions.
Data for the statistical analysis were acquired from a set of CMP processes of phosphosilicate glass (PSG) frequently used in the backend of line process in system IC integration. PSG provides lower dielectric contact over silicon oxide, and reduces the depth of steps created by metallization.
The thickness of PSG thin film as deposited on prime grade
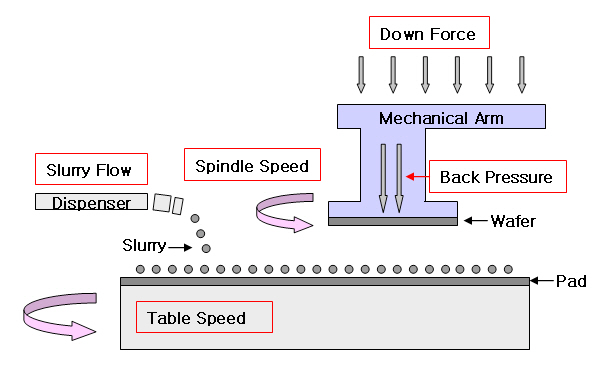
Five controllable parameters were included as input factors in this experiment (Table 1). While a series of designed experiment was performed, other factors, such as types of pad and slurry,table temperature, and pad condition, were controlled without change. Figure 1 schematically illustrates tool operation with the operating parameters.
DOE is a statistically driven experiment design method that provides systematical determination of experimental splits and enables statistical analysis via analysis of variance (ANOVA)and regression modeling. It also visualizes the main effects of
employed parameters and interactions between parameters for given responses of interest, herein RR and calculated percent uniformity.
The benefit of DOE also expands to maximize data analysis with the least number of experiments. If a process has more than a very small number of steps, whose possible values have a large range, the number of experiments needed for process characterization can be prohibitively large. In addition, the role of each step in determining the outcome is generally unclear.The traditionally method of collecting large quantities of data by holding each factor constant in turn, until all possibilities have been tested, is an approach that quickly becomes impossible, as the number of factors increase. Statistical experimental design is a systematic and efficient alternative methodology for characterization and modeling using a relatively small number of experiments.Statistical data analysis was performed by investigating DOE data from 25-1 fractional factorial design with multiple center points.
The randomized experimental run order was strictly followed to avoid experimenter bias or tool condition associated with time. Two responses of interest, RR and percent non-uniformity(NU), were calculated using the following simple equation:
We found with the statistical analysis of the given data set that the percent NU does not follow a normal distribution. Thus, Box-Cox transformation (BCT) was initially taken before any further statistical data analysis. The following section will detail this.
A key underlying assumption in statistics is that the given data follows the normal distribution. It is highly recommended that normality be checked before any statistical analysis. Otherwise,misleading conclusions may result. We have checked the data normality for both responses. The percent NU showed a relatively poor degree of normality. The central limit theorem may be employed to justify the normality check with the limited number
of experiments. However, this may jeopardize statistically driven conclusions. Thus, we have employed Box-Cox transformation with λ = -0.5 for the acquired
The transformed
We performed qualitative analysis to understand the relationships between parameters. Statistical analysis and regression modeling certainly provide a great amount of specific information,but one should have sufficient background knowledge of statistics to interpret the result. However, this paper focuses on qualitative analysis to provide an insight to first-level equipment engineers in their operational processes.
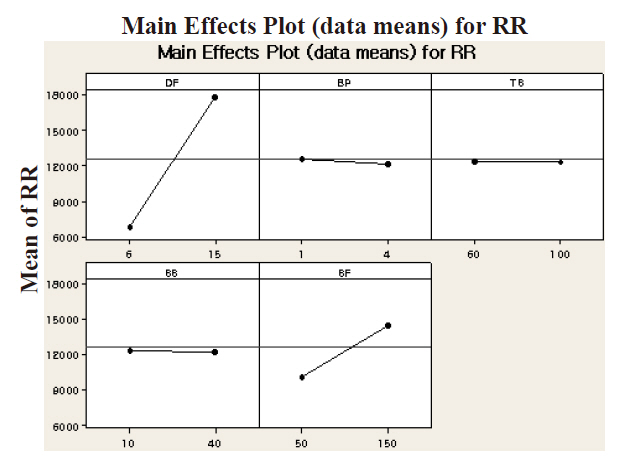
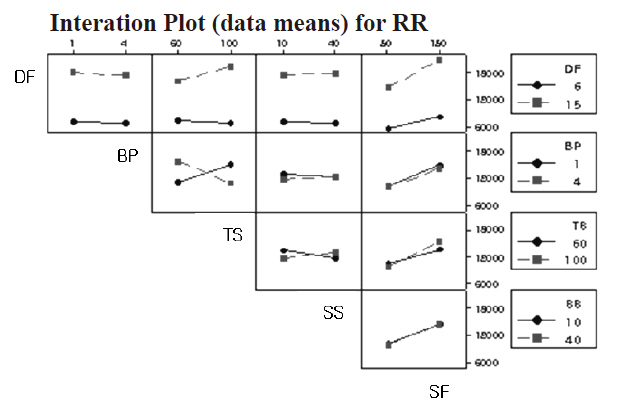
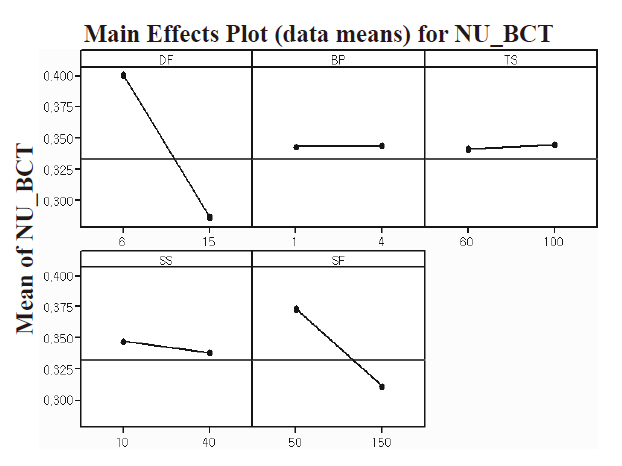
Downward force (DF) and slurry flow (SF) have the most influence.This is not surprising, since the mechanical polishing mechanism is dominant for PSG. The initially considered variables of back pressure (BP), spindle speed (SS), and table speed(TS) were found to be not significant factors from the main effect plot, as shown in Fig. 3. This too is straightforward. Figure 4 shows the interactions of BP-TS and TS-SS with respect to RR,but the interactions reside within insignificant parameters.
Conversely, BP can affect RR with DF, and they have plausibly a similar down-forcing mechanism on the wafer in the process.Qualitative analysis of the two types of plots provides engineers information about the three most important tool parameters to keep constant in their device manufacturing. One can follow the qualitative analysis, such as ANOVA analysis and regression modeling, to help the degree of control required for this specific process, but the numerical analysis is out of the scope of this work. The derived regression equation for the RR is provided below.
RR=182.70+227.47·DF+1.89·BF+5.70·DF·BP-3.66·TS·SS
Only two parameters, DF and SF, are shown to have a statistically significant effect on the NU, from the main effect plot in Fig. 5. However, some interactions between other parameters obviously exist. Qualitative analysis on the percent NU shows similar results to RR, because its calculation includes the average value of RR from a different location.
Stepwise regression modeling was performed to better understand the quantitative information. Initially we have included two-way interactions. This showed a very poor model fit with the R-sq value, as high as 40%. Including three-way interaction terms elevated the model fit almost 60%, but the statistical modeling still has some degree of residuals from the modeling. Providing the built regression equation and ANOVA table will give much detailed information to the analysis. However, the qualitative analysis still conceptually hold when the model fit does not provide a good value of R-sq.
NU=-0.71+0.91·DF+1.29·BF-0.54·SF-0.23·DF·BP+0.01·DF·SF
The statistical modeling might not be suggested to be as good as we expected. However, we did find that DF and slurry flow (SF)are the most significant factors in CMP. In addition, Wafer BP interacts with the DF to change of RR, and SS can interact with slurry flow (SF) in terms of CMP uniformity. These tool parameters should be tightly controlled to increase process yield for successful semiconductor manufacturing.
Five parameters associated with process characterization were investigated. Their effects on RR and NU were determined using regression equation. The analysis shows the main effects, DF, BP,TS, and their two and three way interaction terms were statistically significant. Ultimately, NU is a complex response resulting from the high degree of interactions of more than two parameters,and the control of NU in larger wafer fabrication process is very valuable, especially in a high volume-manufacturing environment.The RR of the CMP process is mainly affected by DF and SS. However, some degree of interactions obviously exists that we can no longer ignore.