The current study analyzes the effects of the scaling parameters of the batch unscented transformation on precision satellite orbit determination. Satellite laser ranging (SLR) data are used in the orbit determination algorithm, which consists of dynamics model, observation model and filtering algorithm composed of the batch unscented transformation.TOPEX/Poseidon SLR data are used by utilizing the normal point (NP) data observed from ground station. The filtering algorithm includes a repeated series of processes to determine the appropriate scaling parameters for the batch unscented transformation. To determine appropriate scaling parameters, general ranges of the scaling parameters of α, β, κ, λ are established. Depending on the range settings, each parameter was assigned to the filtering algorithm at regular intervals. Appropriate scaling parameters are determined for observation data obtained from several observatories, by analyzing the relationship between tuning properties of the scaling parameters and estimated orbit precision. The orbit determination of satellite using the batch unscented transformation can achieve levels of accuracy within several tens of cm with the appropriate scaling parameters. The analyses in the present study give insights into the roles of scaling parameters in the batch unscented transformation method.
Determining the orbit of satellites more accurately has become a much more significant objective. In terms of precise satellite tracking technology, satellite laser ranging (SLR) holds the normal point (NP) accuracy of mm,and the accuracy of single shot in cm (Montenbruck &Gill 2000). With this high level of accuracy, SLR can be easily applied to the independent revision of other satellite tracking systems, and is used in various fields of application, such as verifying the effectiveness of the Global Navigation Satellite System (GNSS), space geodesy, the Earth’s gravitational field, displacement of the Earth's crust and geodynamics (Zhu et al. 1997, Biancale et al.2000, Urschl et al. 2007). For the high accuracy of the SLR system in order to more precisely fulfill the function of determining the orbit of a satellite, an accurate kinematic model and the existence of an observation model that minimizes error become important elements. Satellite orbit determination software is largely composed of the dynamic model, observation model and filtering algorithm. To precisely determine the orbit of a satellite, it is necessary not only to model the elements that influence the motions of the satellite, but also to model the environmental factors according to observation data and equipment when gaining the tracking data of the satellite,and reflecting those results in the process of calculation.It is also very important to choose a filtering algorithm for the process of minimizing the residual between actual observation values and calculated observation values.
In filtering algorithms used for orbit determination, there is the consecutive method that is enabled for real-time estimation, and a batch processing method based on the principles of the least-squares method that uses the data observed in the past. Both of these filtering algorithms have the following restrictions when using the SLR data. First, since there are currently about 40 SLR satellites and about 50 SLR ground stations around the world, the amount of SLR data is not sufficient. Second, since it is difficult to continuously track satellites due to the small number of satellites and ground stations, such an approach has the disadvantage of being unsuitable for real-time processing. Finally, the dispersion of discontinuous data means that there are ways in which errors may be induced, or the functions of filters restricted. For this reason, based on processing the data through the batch processing method, the batch unscented transformation method (Park et al. 2007) is applied to overcome the error elements that result from the small amounts of data and the discontinuous data dispersion. The unscented transformation that becomes the foundation of the batch unscented transformation method is the method of predicting the mean and covariance from the non-linear system. Since it uses the sigma points of specific numbers and does not use the random sampling of the Monte Carlo method, it is possible to gain the maximum results in a short period of time (Julier 2002, Julier & Uhlmann 2002).
The state of the sigma point is initially created, which influences the accuracy of orbit estimation when using the batch unscented transformation method for the precision orbit determination (POD). To determine the state of the sigma point, the initial covariance and the scaling parameter are required (Howlett et al. 2004). Deciding how to set the scaling parameters influencing the resolution of the sigma points will change the results of the estimation algorithm, and furthermore will contribute to increasing the accuracy of orbit determination. In other words, according to the scaling parameters in the batch unscented transformation method, the precision and the convergence performance of the orbit determination may be changed. The scaling parameters
2. BATCH UNSCENTED TRANSFORMATION
In this section, batch unscented transformation (Park et al. 2010) is briefly reviewed to explain the scaling parameters in the process. The batch processing method estimates the states by using overall observation data in a selected orbit section. Meanwhile, the sequential processing method estimates the states within each of the observation times. Within the sequential processing method with no process noise, the algorithms between the methods hold a mathematical similarity. Therefore, the typical unscented Kalman filter (UKF) is very useful in materializing the new batch unscented transformation method (Park et al. 2010). The batch unscented transformation method for orbit determination has the following assumptions. If observational noise can be considered a fixed value, the algorithm can be derived from the Kalman filter. Therefore, the state and covariance are expressed in the following Eq. (1) for the UKF,
where
First, when assuming the estimation for the covariance with the initial state with Eq. (2) to obtain the sigma point, it is as displayed in Eq. (3), where
In the UKF, the states are propagated to the following observation time to renew into a greater value through the non-linear dynamic model Eq. (4). However, since the batch unscented transformation filter uses all of the values observed during the entire period to accomplish the estimation, the sigma points propagated are the same as the estimated values of the past. Therefore, Eqs. (4-6) do not have to be calculated, and the propagated state and the covariance within the chosen time can change as in Eq. (7).
The sigma points (
The χi,j(i,e. χi,1χi,2,..,χi,N) on the right term of Eq. (8) are the sigma points propagated
Finally, the state in time
Here, ΔZ
3. SCALING PARAMETERS IN THE BATCH UNSCENTED TRANSFORMATION
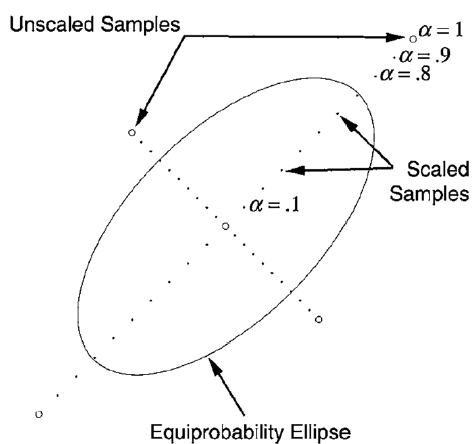
First of all, setting the scaling parameters in the batch unscented transformation affects the precision and the convergence performance of the orbit determination, because the scaling parameters influence the formation of the sigma point in the process of unscented transformation. Accordingly, it can be observed that the scaling parameters play an important role in the process of orbit determination. The unscented transformation becomes a basic process for the batch unscented transformation method, and the transformation evaluates the mean and covariance from the non-linear system. The batch unscented transformation is similar to the Monte Carlo method with numerous sigma points, but it does not use numerous sigma points randomly but rather uses the sigma points described in Eq. (2) for a smaller sigma point. In general, the sigma points are composed of one mean and covariance, which are determined by the number of dimensions. The scaling parameter concept of unscented transformation is a further application of the symmetric unscented transformation that allows some sampling and weighting adjustments to improve strength against higher order non-linearities. It uses four adjustable scaling parameters
Suppose
The sigma points can be scaled towards and away from the mean of the prior distribution by appropriately selecting
The positive scaling parameter α and the secondary scaling parameter κ can be combined into scaling parameter
Here, Δ
4. SIMULATIONS AND DISCUSSIONS
The purpose of the present study is to investigate the roles of scaling parameters of the batch unscented transformation method for the POD of a satellite using the SLR observation data. The dynamic equation is composed using Cowell's method (Vallado & McClain 1997), and the observation data is actual TOPEX/Poseidon SLR data. The Earth gravitational model 1996 (EGM96) (Lemoine et al. 1998) is used for the numerical model for the Earth's asymmetrical gravitational field, and the Jacchia 71 model (Lyndon 1982) is used as the density function to calculate the atmospheric refraction (Marini & Murray 1973). Moreover, the perturbations by the gravitation of the Sun and the Moon and the perturbation of the Sun's radiation pressure are considered, and the Earth’s crust and tidal force from the Sun and the Moon are also considered. For the numerical integration of the dynamic model, the Adams-Cowell method, one of the multi-step methods, is used. The observation model postulates the 4 ground observatories positioned on the surface of the Earth (McDonald, Monument, Borowiec, Herstmonceux), and utilizes the range data between the satellite and the ground observatory observed from each of the observatories as the observation data. As the filtering algorithm, the batch unscented transformation filter is applied. When using the batch unscented transformation method, the scaling parameters affect the precision and the convergence performance of the orbit determination. It can be observed that the scaling parameters play an important role in the process of orbit determination. Four adjustable scaling parameters
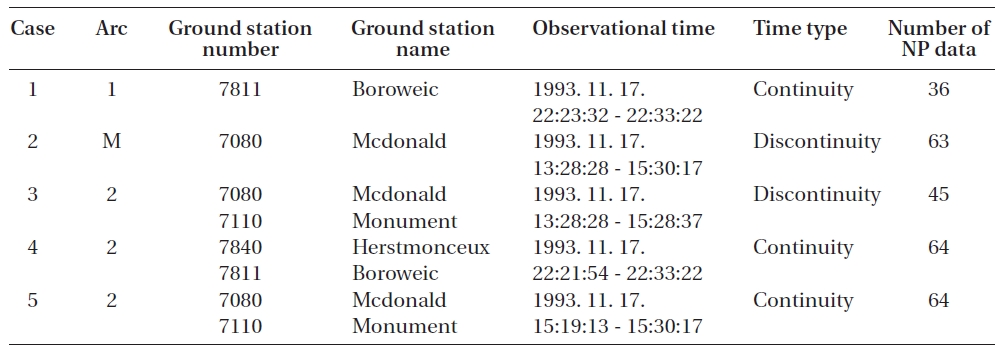
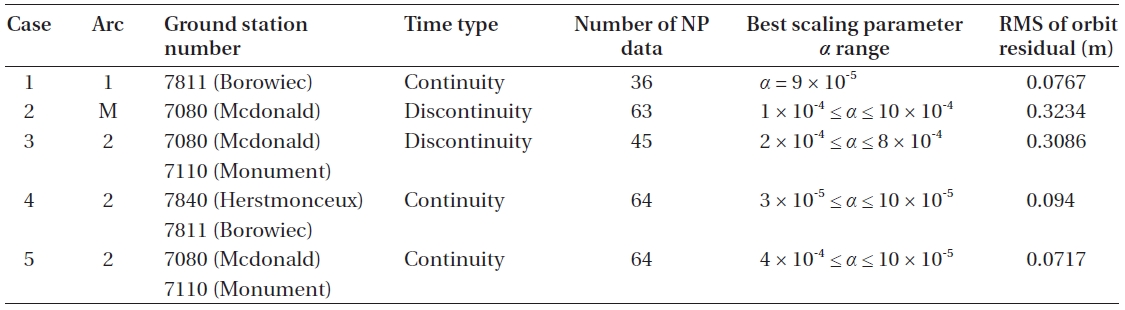
[Table 1.] The ground station and observational data information.
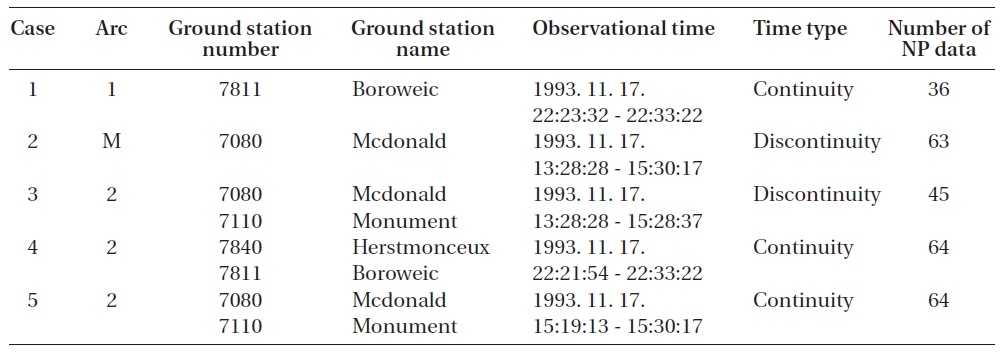
The ground station and observational data information.
To verify the precision orbit determination, the results of the orbit determination are compared with ephemeris by Jet Propulsion Laboratory1 (JPL) that are assumed to be true orbits. The official ephemeris of TOPEX/Poseidon was calculated through the differential global positioning system (DGPS) method using the global positioning system data (Melbourne et al. 2007). The POD error with DGPS method is approximately 2 cm RMS on the radial direction (Bertiger et al. 1994, Schutz et al. 1994, Yunck et al. 1994).
The paper attempts to simulate four types of tests depending on the characteristics of the observatories from arc information of Table 1, which include arc number, ground station number, ground station name, observational time, time type, and the number of normal point data. The orbit determination results are composed of no initial position error, 10 m error, 100 m error, and 1 km error of initial position, respectively. Here, the position errors are computed for radial, along, and cross direction. To verify the self performance of the POD, the orbit determination is performed when the initial state error was 0. The initial state is composed of position and velocity from the interpolation value of ephemeris on epoch time by JPL. The simulation results consist of four kinds of cases that depend on the observational data type. To find the appropriate scaling parameters, the simulations are performed for four cases, such as case 1 (applying one arc to one base station), case 2 (applying multi-arc to one base station), case 3 (applying two arcs from discontinuous observation time for two base stations) and case 4 (applying two arcs from continuous observation time for two base stations).
In this research, the number of dimensions
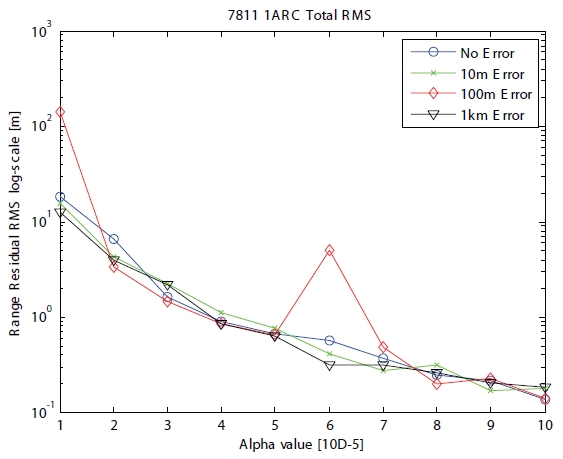
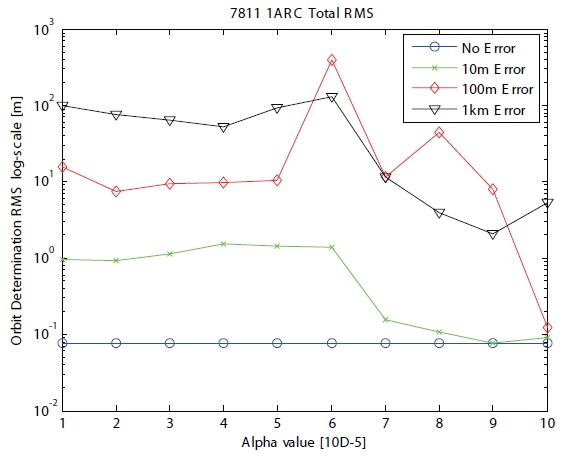
Case 1 applies one arc to one ground station (Boroweic).The initial orbit elements are given as position and velocity vectors. The number of total iterations is ten for the batch unscented process. The iteration process is stopped when the iteration number reaches a total iteration number, or when the gap of previous and present RMS errors is smaller than the arbitrary convergence criterion(2 × 10-2) chosen to maintain the best performance of the simulation. The values of initial position covariance and velocity covariance are fixed as 10-2 m and 10-8 m/s respectively, because they are similar to the errors of initial orbit elements from ephemeris. Moreover, the initial velocity covariance is generally less than the initial position covariance (Park et al. 2007). The information of observational data and ground station for case 1 is shown in Table 1. Strictly speaking, the time type of case 1 is similar to continuity. True position refers to the actual satellite position from the precision orbit ephemeris (POE) by JPL, and the estimated position is obtained from the final value of POD. The orbit residual is calculated from the difference between the true position and the estimated position as the RMS represented by following equation. Here,
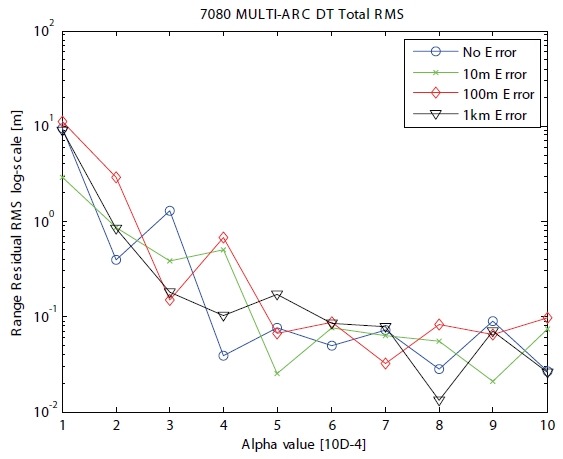
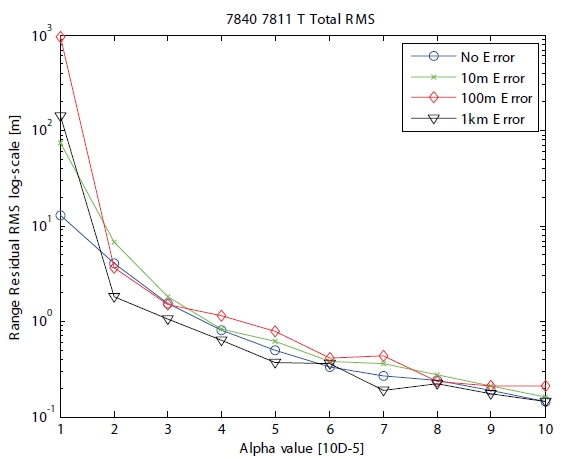
The RMS of range residual shown in Fig. 2 according to the positive scaling parameter
focused on tuning the scaling parameter when the initial error was 10 m. When the scaling parameter
5, the RMS of orbit residual in the case of 10 m position error is about 8 cm, which is a similar result to no initial position error.
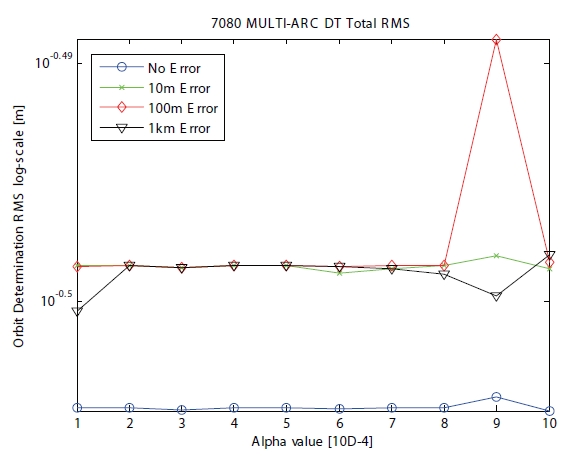
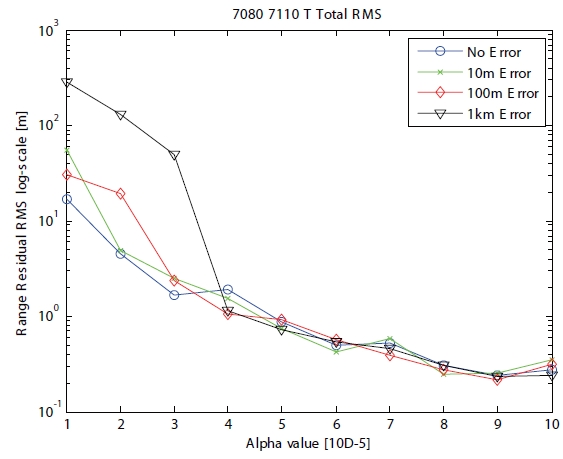
Case 2 is applied for multi-arc to one ground station, and is shown in Table 1. The time type of case 2 has discrete characteristics. The initial position errors are assumed as none, 10 m, 100 m and 1 km. The RMS of range residual shows in Fig. 4 according to the positive scaling parameter
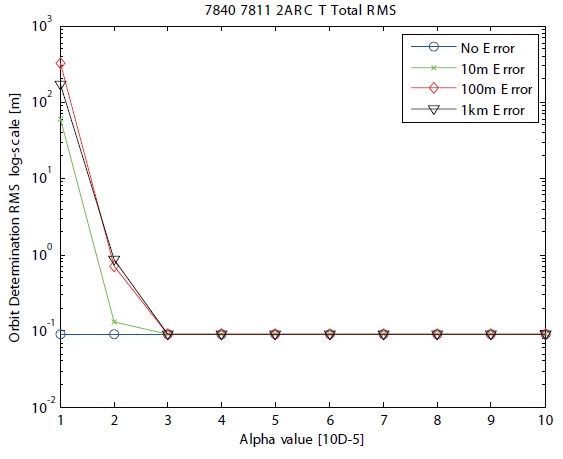
Case 3 is applied for two arcs to two ground stations, and is presented in Table 1. The time type of case 3 has discrete characteristics with different observation times in two ground stations. The RMS of range residual is shown in Fig. 6 when the positive scaling parameter
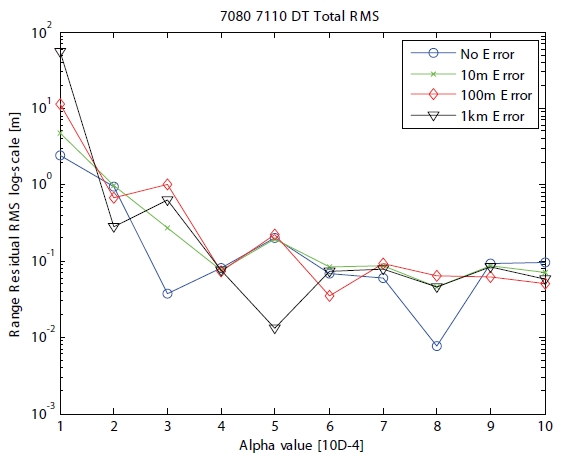
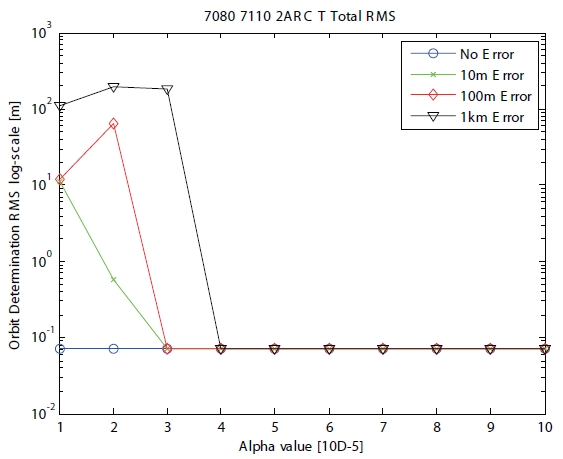
The information of observational data and ground station in Table 1 is provided for case 4 applied to two arcs to two ground stations. The observation time of case 4 has a continuous attribute with the same time in two ground stations. In other words, the observation method of case
4 means that two ground stations observe the same target at the same time. The RMS of range residual shown in
Fig. 8 as the positive scaling parameter
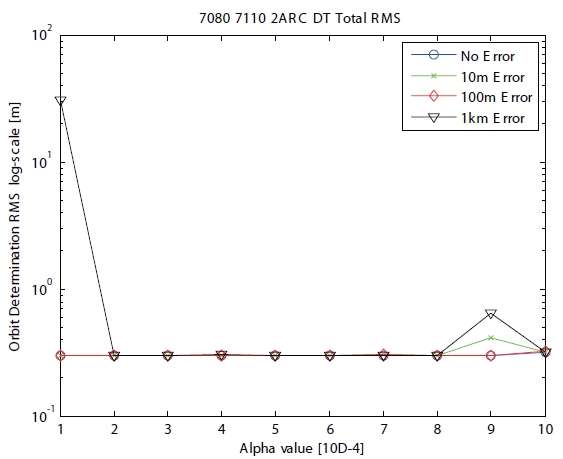
Case 5 is applied for two arcs with two ground stations, and is presented in Table 1. The time type of case 5 has continuous features, with the same observation time in two ground stations. The RMS of range residual is shown in Fig. 10 when the positive scaling parameter
Table 2 provides the summarized information of simulation results, including arc number, ground station number and RMS of orbit residual according to the range of the best scaling parameter
[Table 2.] The best range of scaling parameter α.
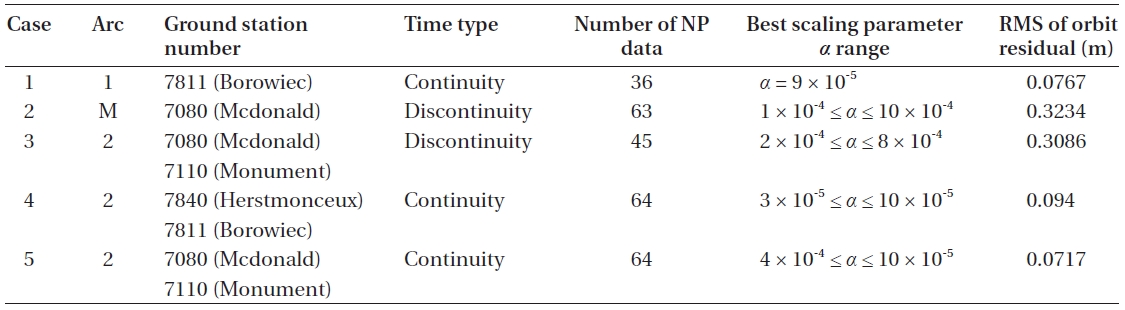
The best range of scaling parameter α.
algorithm in one arc of Borowiec station with an appropriately tuned scaling parameter
In conclusion, more precise results were gained when the observation data existed as a continuous time type, and the value of scaling parameter
1ftp://podaac-ftp.jpl.nasa.gov/allData/topex/ [cited 6 May. 2010]
The values of scaling parameters in the batch unscented transformation method can change the accuracy and the convergence performance of the orbit determination.The purpose of this research was to determine the roles and contributions of the scaling parameters in orbit determination using the batch unscented transformation method. The major factor of orbit determination within the batch unscented transformation method is the state of the initial sigma points made from the scaling parameters. The physical meaning of the scaling parameters is a numerical value that determines the distribution and range boundary of sigma points. Thus, the scaling parameters are analyzed in order to understand their physical meaning for POD using SLR data. The appropriate scaling parameters are determined, and the tuning properties of the scaling parameters are analyzed for several observation data. Rather than the empirical value of the scaling parameters, the generally acceptable range of the scaling parameters is considered to improve the accuracy of the orbit determination algorithm. The process of creating the sigma points affects the accuracy and converging performance. Errors can be minimized by appropriately tuning the scaling parameters. Therefore, the fine tuning of the scaling parameters can improve the accuracy of the orbit determination results from the TOPEX/Poseidon SLR observation. If you use the batch unscented transformation method with other types of tracking data, the task of finding the appropriate scaling parameter must be carried out first. In this research, it is confirmed that the distributed range of the sigma points is strongly formed by the scaling parameter alpha, which is one of the applied factors within the converging performance of the orbit determination system.