Global positioning system (GPS), the wireless navigation system based on satellite, stated to be developed in early 1970’s by U.S. Ministry of Defense. The first GPS satellite was launched in 1978 and the regular operation of GPS began in 1994. GPS is the navigation system that can provide service to the entire globe regardless of time and the meteorological conditions. Although it was initially developed for military purpose, its use has been rapidly extended to civilian areas and it is now widely and generally used for navigation, tracking, position determination, time synchronization, etc.
GPS employs two measurements to calculate position:pseudo-range code and carrier phase. Since approximately 10 m of position precision can be obtained through simple calculation using the measured code values, the code values are generally applied mainly for real-time mobile navigation and tracking system. The position resolution of centimeters can be obtained if the carrier phase measurements of high resolution are used, but there exists initial integer ambiguity since the preciprecise number of cycles taken by the transmitted carrier phase to reach the user cannot be known. Because a complicated calculation process is required to determine the ambiguous integers precisely, the position determination using carrier phase is usually applied to special purposes such as geodesy, mobile attitude determination and precise orbit determination (POD) of low earth orbiter (LEO), after undergoing post-processing.
The GPS receiver is loaded on a satellite to obtain the navigation solution with respect to position and velocity as in the case of ground GPS receiver. In addition, the precise orbit information obtained by means of ground post-processing of the raw measurements of pseudo-range code and carrier phase is used for ground observation, satellite image quality improvement, and atmospheric observation. The GPS receiver loaded on LEO is chosen between single frequency receiver and dual frequency receiver depending on how precisely the ionosphere error will be eliminated by the satellite position precision required for the satellite’s mission. If a dual frequency GPS receiver is used, the ambiguous integers can be determined more precisely since the precise carrier phase data from which almost all the ionosphere error is eliminated can be obtained. The root mean square (RMS) of satellite orbit resolution determined by a single frequency GPS receiver is one meter approximately, while it becomes more precise to tens of centimeters if a dual frequency GPS receiver is used. The satellite position precision demand for the Korea Multi-Purpose Satellite (KOMPSAT)-2 to carry out the mission to take precise images, which is one meter, is satisfied by the POD using the measurements obtained from a single frequency GPS receiver (Lee et al. 2005, Hwang et al. 2007). However, since the KOMPSAT-5 is supposed to carry out the mission to take synthetic aperture radar (SAR) images and more precise resolution, which is 20 cm, is required for this assignment, a dual frequency GPS receiver is loaded on it.
The positions determined by means of GPS include absolute position and relative position. The absolute position is determined by a single position determination using one GPS receiver, while the relative position is relatively determined by the differences of the carrier phase measurements among at least two GPS receivers using baseline or network predicting technique. Among the GPS receivers, at least one reference station receiver should have the precise positional information in advance. The precision of relative position determination is higher than that of absolute position determination because the clock error between the GPS satellite and GPS receiver can be eliminated and the effects of the ionosphere and convection layer error are reduced as the baseline is shorter. For these advantages, relative position determination is applied in various areas of geodesy. However, relative position determination also has drawbacks: the precision is dependent upon the measuring precision of the reference station; and the reference station receiver and the user receiver must have identical GPS satellite measurements simultaneously.
Thanks to the advantage that the common clock error can be eliminated in the POD of LEO, the double difference method has been widely applied to the carrier phase measurements of LEO and the International GNSS Service (IGS) that is distributed worldwide. It was verified that KOMPSAT-5 can also satisfy the required position precision through the double difference method as in the case of KOMPSAT-2 (Hwang et al. 2009). The precise LEO orbit determination using double difference data has additional difficulties that a lot of the ground IGS network measurements should be processed and the precise IGS position information should be tracked. In particular, KOMPSAT-5 requires near real-time (NRT) POD to make possible weather forecast through GPS radio occultation observation (Bock et al. 2002, Rothacher et al. 2007). The conventional method based on double difference is limited because of the drawbacks mentioned before and thus NRT POD cannot be performed with that method.
The alternative method that is coming to the fore is precise point positioning (PPP). Since PPP is the absolute positioning technology in which the satellite’s own position is determined with only one receiver, as in the case of code-based single positioning using the GPS broadcast ephemeris, without the measurement by a receiver in a specific area or a wide-range reference station, the calculation is relatively simple and, in particular, it is very economical in the application areas requiring wide-range reference station such as LEO POD. Different from the general code-based single positioning, PPP shows the precision of centimeter in the case of a fixed ground receiver and the precision of tens of centimeters in the case of mobile receiver with a dual frequency GPS receiver, precise orbit ephemeris and high precision clock information as well as the carrier phase measurement (Ovstedal et al. 2006). Many studies are actively conducted to perform NRT orbit determination in a relatively simple method by applying the LEO POD to PPP, obtain the precision similar to that of differential GPS (DGPS) or compare with each other (?vehla & Rothacher 2003, Jaggi et al. 2007, Peng & Wu 2007, 2009, Roh et al. 2009, Li et al. 2010).
KOMPSAT-5 requires 20 cm of satellite position precision to process the high-resolution SAR images and carry out the assignment of GPS radio occultation observation. Thus, the integrated GPS and occultation receiver (IGOR) payload which succeeded the Blackjack receiver, the high resolution dual frequency GPS receiver developed by Jet Propulsion Laboratory (JPL) and loaded on CHAMP, the Gravity Recover and Climate Experiment (GRACE) and JASON-1 satellites for scientific purposes is loaded on KOMPSAT-5 as in the case of the German satellite, TerraSAR-X, which was launched in July, 2007, with the same missions of KOMPSAT-5 (Montenbruck et al. 2006, Rothacher et al. 2007). Since NRT POD is needed to satisfy the urgent image processing requirements and make meteorological forecast possible through the GPS radio occultation observation, the PPP method that has the same level of position precision with the double difference method is effective.
In the PPP, we used the actual GPS raw measurements (GPS1B) of GRACE that was launched in 2002 and is now carrying out the mission to measure the changes in the earth’ gravity field. The orbit determination was performed by using the reduced-dynamic method and the kinematic method. The results were verified with the precise orbit ephemeris (GNV1B) provided together to JPL. The GPS raw measurements (GPS1B) and the precise orbit ephemeris (GNV1B) of the GRACE satellite was extracted from the Level 1B data that JPL opens to the public (Case et al. 2010). We used Bernese GPS software 5.0 developed in University of Bern, Switzerland, as the orbit determination software.
In the geodesic field, the PPP of centimeter precision that is a single positioning method using the post-processed precise orbit ephemeris from IGS instead of broadcast ephemeris, the high-precision satellite clock correction terms, and carrier phase measurement from the dual frequency GPS receiver was suggested as an alternative of DGPS that is highly precise (Zumberge et al. 1997, Kouba & Heroux 2001). PPP basically has the same concept of standard positioning service and, additionally, the methods to effectively eliminate the errors that affect the measurements such as ionospheric time delay, satellite orbit error, satellite clock error, convection layer delay and multipath error to improve the precision.
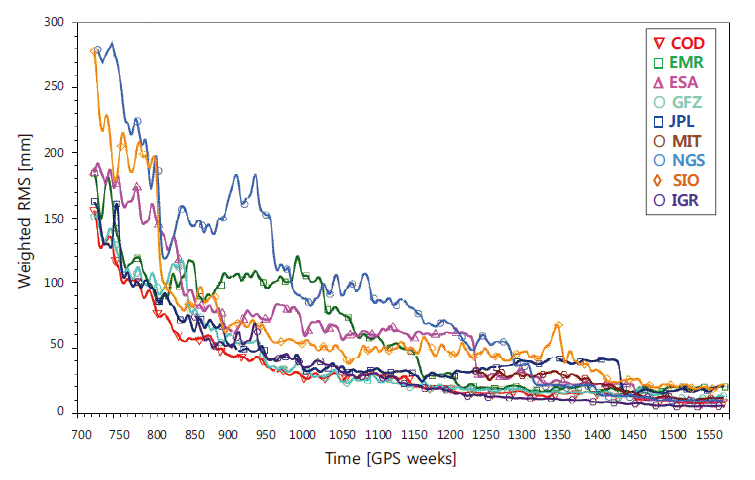
The ionospheric time delay, which is the largest GPS error factor after the elimination of selective availability, is eliminated mostly by the linear combination of krthe phase measurements of the L1 and L2 frequencies. The GPS satellite orbit error can be greatly improved using the precise orbit ephemeris provided by IGS after the post-processing of GPS orbit satellite. Since 1994, IGS has provided GPS satellite precise orbit ephemeris with improved precision and timeliness. Fig. 1 compares the orbit ephemeris post-processed individually in the IGS rapid (IGR) and eight IGS analysis centers in last 16 years and the final combined IGS orbit ephemeris, showing that the precision has been improved from 30 cm to 1-2 cm.
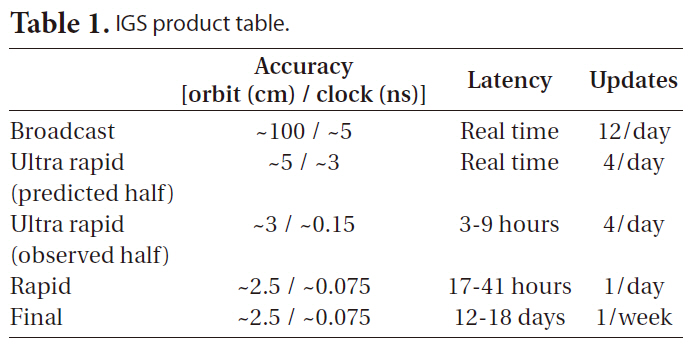
The IGS precise orbit ephemeris is provided in three different types, as shown in Table 1, and the orbit precision is 20 to 50 times higher than that of broadcast ephemeris which is approximately 100 cm. Ultra rapid (IGU) can be used for the NRT applications and it is updated in every six hours with 3 hours of latency, retaining the data of 48 hours. The first 24-hour data, the post-processing results of the measurements, has 3 hours of latency, while the second 24-hour data, the predicted values of satellite orbit and clock information, can be processed in real-time
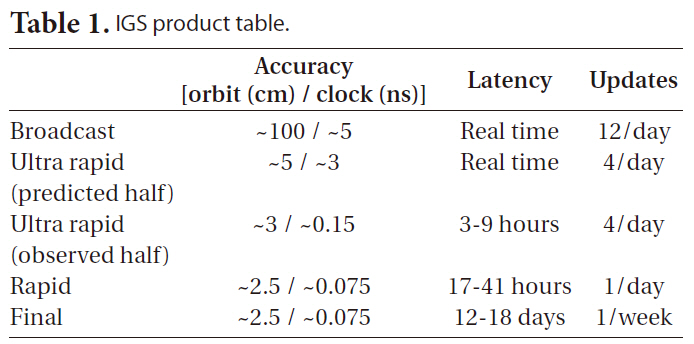
IGS product table.
because there is no time delay. Thanks to the precise orbit model of GPS satellite, the predicted IGU orbit precision is about five centimeters which can be used for NRT LEO PPP sufficiently. However, since the long-term prediction of clock information is impossible because of the non-deterministic nature, the clock precision is about 20 times lower.
To solve the satellite clock error, the correction data of 30 second interval, which is more precise than the conventional satellite clock correction data of 5-minute interval, is provided by Center for Orbit Determination in Europe (CODE) from January, 2004 and by JPL from December, 2006. For the applications requiring GPS measurements that is highly precise and has the interval shorter than 30 seconds, CODE has provided 5-second clock correction data since April, 2008. However, these data are not appropriate to NRT PPP because the data are provided about 5-12 days later. Since the data interval of IGU precise orbit ephemeris is 15 minutes, more precise GPS satellite clock correction data is needed for PPP. Thus, the study is carried out to estimate high-precision clock correction data through IGU precise orbit ephemeris and ground IGS tracking (Bock et al. 2009).
In addition, the error by the convection layer time delay is not considered because most of LEOs are operated at the altitude higher than 200 km above the convection layer and thus free from the effect. Also, the multipath error is usually negligibly small, but it can be reduced further by setting the antenna elevation mask angle to 5˚ (Li et al. 2010). Hence, PPP can be applied not only to meteorological forecast but also to precise navigation and satellite formation flying, because NRT PPP is possible if highly precise clock correction data is provided from IGS or self-estimated.
3. PRECISE ORBIT DETERMINATION
The methods to express the orbit dynamics by means of satellite precise orbit determination include the dynamics, reduced-dynamics and kinematic methods. In the dynamics method, the orbit is determined more precisely as the satellite motion equation expresses as many perturbation factors as possible through modeling, but the precise modeling of perturbation is more difficult and the precision is lowered as the altitude of a satellite is lower. In the kinematic method, the orbit is estimated on the basis of GPS measurement, not using the equation of the orbit motion, in the same way that the trajectory of a car or ship on the ground level is tracked. Although this method is not affected by the altitude, it requires estimation of a number of parameters. The reduced-dynamics method, which is the combination of the dynamics method and the kinematic method, employs a relatively simple dynamic equation and statistically estimates the LEO orbit as a parameter by introducing the pseudo-stochastic pulses concept or the system noise concept in motion equation for the processing of the acceleration vectors that cannot be expressed by modeling or that have been wrongly modeled. Among these methods, we used the reduced-dynamics method and the kinematic method for orbit determination, because the precision of those two methods is generally higher than that of the dynamic method (Gill & Montenbruck 2004).
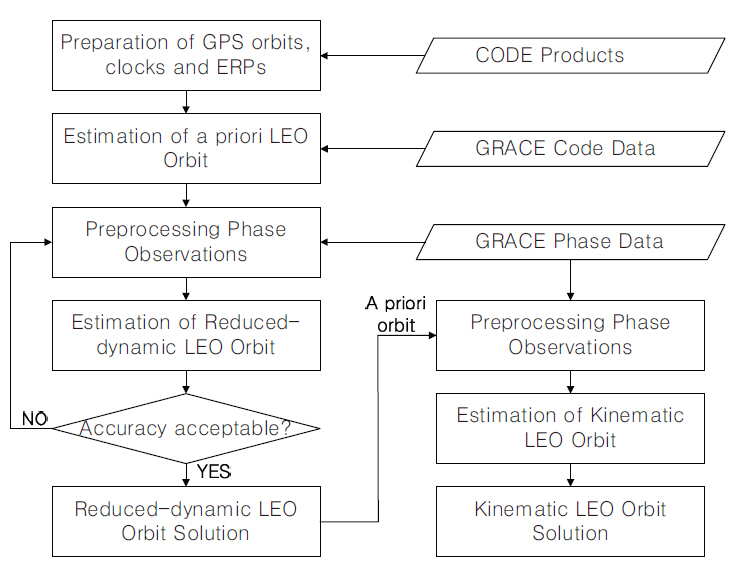
Fig. 2 shows the flow chart of the GRACE satellite POD by the reduced-dynamic method and the kinematic method using PPP. The procedure of the reduced-dynamic method is shown at the right side of the figure. The first step is the preparation step where the precise orbit ephemeris, high-precision clock correction data and the earth rotation parameter are downloaded all from one CODE site so that the data can be synchronized and they are converted to the Bernese GPS software types. In the second step, a priori orbit of the GRACE satellite that is needed for the reduced-dynamic method is estimated on the basis of the CODE observation data among the raw measurements (GPS1B) extracted from the GRACE Level 1B data provided by JPL. The third step is an important step of pre-processing of the GRACE phase observation data where the faulty data are eliminated and the cycle slips are detected and corrected. The pre-processing parameter setting greatly influences the precision of the fi-
nal orbit determination. In the fourth step, the reduced-dynamic orbit is estimated using the phase observation data pre-processed in the previous step. The parameters of the epoch-difference method for the pre-processing in the third step were precisely set stepwise to obtain the required position precision. The mean RMS of the epoch-difference solution was considerably improved after implementing the step for two times, when compared with that after the first implementation, but the result was converging after the third implementation without showing a significant difference with that after the second implementation. For example, in the case of May 23, 2009 (the 143rd day), the mean RMS was 6.07 cm after the first pre-processing, and it was improved to 0.79 cm in the second pre-processing, but it was converged to 0.74 cm after the third pre-processing. Thus, the orbit information was repeatedly updated up to three times to determine the final precise reduced-dynamic orbit.
The left side of Fig. 2 shows the kinematic method where the precise orbit is determined depending on the pure GPS measurements, not by the orbit motion equation. Since the pre-processing result of the GPS phase measurements was an important factor to the precision of the kinematic method, we used the precise orbit obtained by the reduced-dynamic method as the priori orbit used in the phase measurement pre-processing. In contrast to the reduced-dynamic method, the faulty data are eliminated and the cycle slip is detected and corrected without repetition. The precision of the GRACE precise orbit obtained by the reduced-dynamic method and the kinematic method is verified using the GRACE satellite precise ephemeris (GNV1B) extracted from the GRACE Level 1B data provided by JPL.
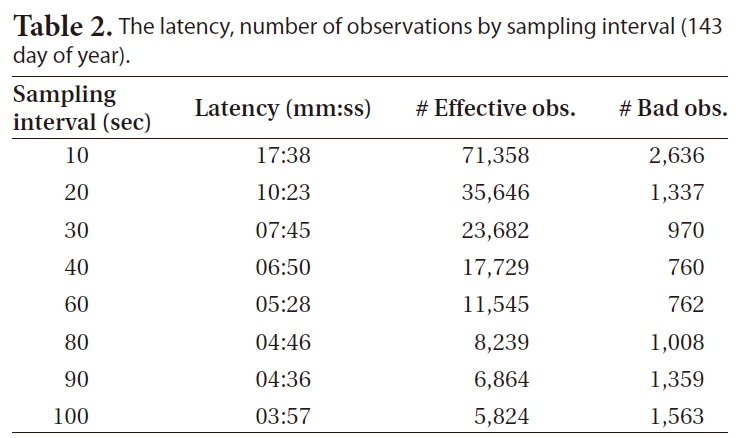
The results of the POD of the GRACE-A satellite through PPP were obtained using the reduced- dynamic and kinematic methods with the 24-hour unit measurements data of 10 days from May 22 to May 31, 2009 (from the 142nd day to the 151st day). Since the GRACE GPS measurement data are provided in 10-second interval, the 5-second interval high-precision GPS clock error data provided by CODE were extrapolated and the sampling interval was gradually increased from 10 seconds to 100 seconds to analyze the orbit determination precision. Since the amount of data is reduced as the sampling interval becomes longer, the time for the orbit determination calculation is reduced as much. Table 2 shows the orbit determination delay time with a general personal computer using the 24-hour GPS data, indicating that the delay time was reduced when using 90-second or 100-second sampling data by up to one fourth of the delay time when using 10-second sampling interval.
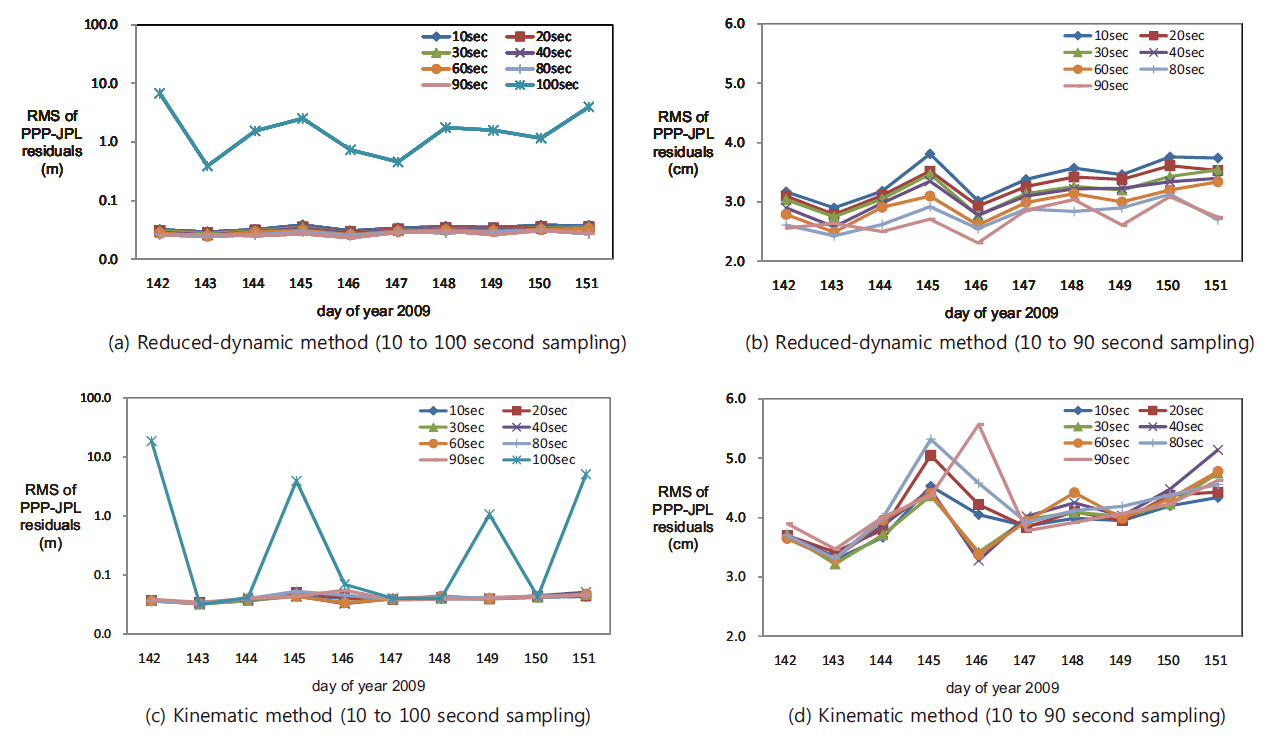
Fig. 3 shows the mean residual at each day by comparing the PPP LEO POD results with the precise orbit ephemeris provided by JPL post-processed POD, depending on the sampling intervals from 10 seconds to 100 seconds. Figs. 3a and b show the results by the reduced-dynamic method and Figs. 3c and d show the results by the kinematic method. Figs. 3b and d show the results excluding the 100-second sampling interval measurements showing large mean residuals as in Figs. 3a and c. When the sampling interval was 10 to 90 seconds, the mean residual was about 3 cm in the reduced-dynamic method and about 5 cm in the kinematic method, but the mean residual was larger than several meters when the sampling interval was 100 seconds. The reason for this may be because the number of faulty measurements was increased as the number of valid measurements basically decreased as shown in Table 2. The number of faulty measurements was decreased as the sampling interval was increased until 40 seconds, but it was increased from the sampling interval longer than that. This may be because some of the neighboring measurements were recognized as faulty measurements when the change of the measurement was great as the sampling interval was increased. The orbit determination precision may be increased by adjusting the faulty measurement detection/correction parameter in the measurements pre-processing step so that the number of faulty measurements can be reduced and the number of valid measurements can be increased. This result indicates that centimeter level POD is possible without losing precision even if the orbit determination latency is reduced by varying the sampling interval from 10 seconds to 90 seconds.
[Table 2.] The latency number of observations by sampling interval (143 day of year).
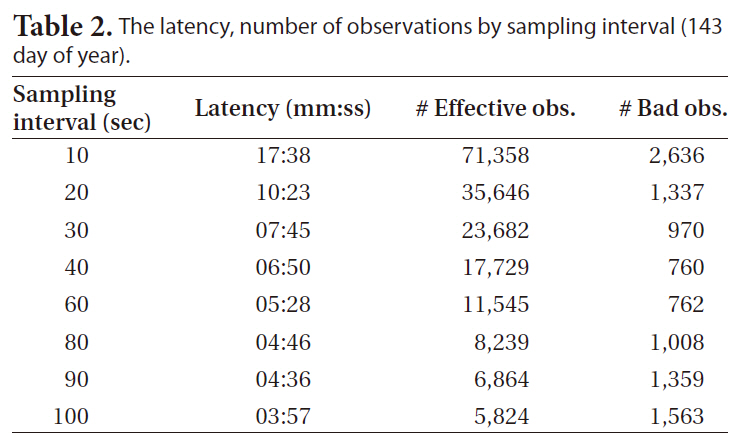
The latency number of observations by sampling interval (143 day of year).
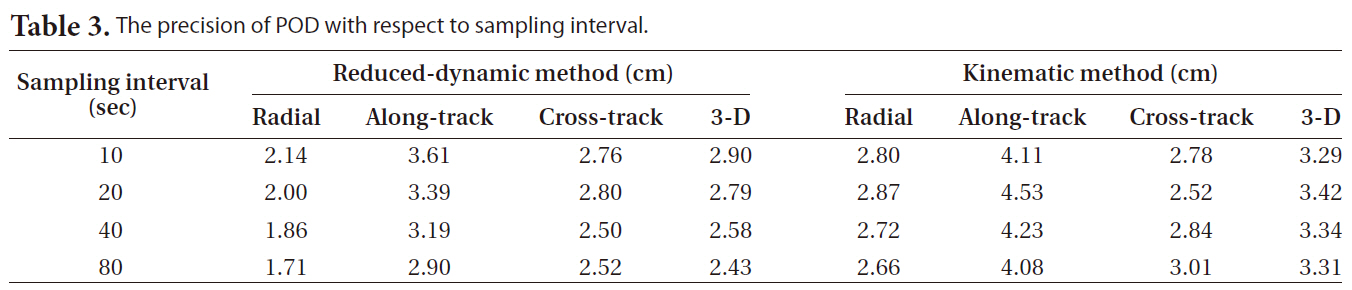
[Table 3.] The precision of POD with respect to sampling interval.
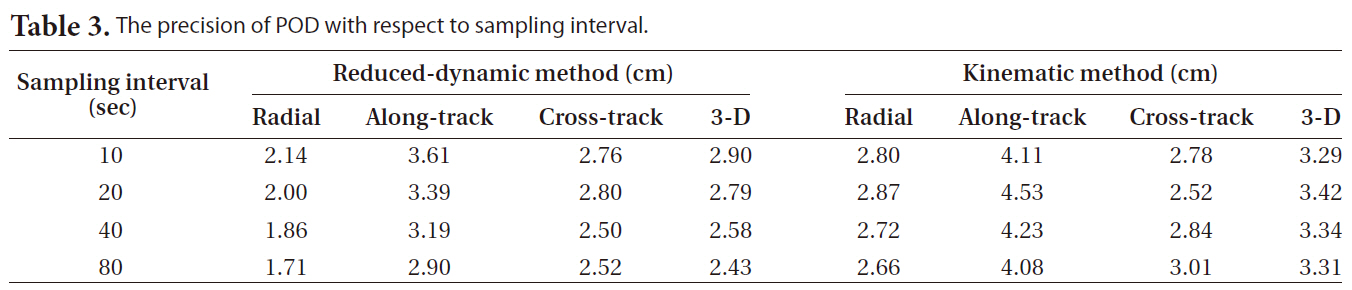
The precision of POD with respect to sampling interval.
Additionally, the precision was varied not only by the sampling intervals but also by the individual days. This suggests that the quality of the raw measurement data basically affects the orbit precision. Also, it was noted that the precision pattern over the days was similar in the kinematic method and the reduced-dynamic method. It indicates that the precision of the kinematic method was influenced by the precise orbit ephemeris obtained by the reduced dynamic method, the priori orbit used in the pre-processing step which determined the quality of the phase measurements that affect the orbit precision, since the precise orbit was determined with the pure GPS measurements in the kinematic method.
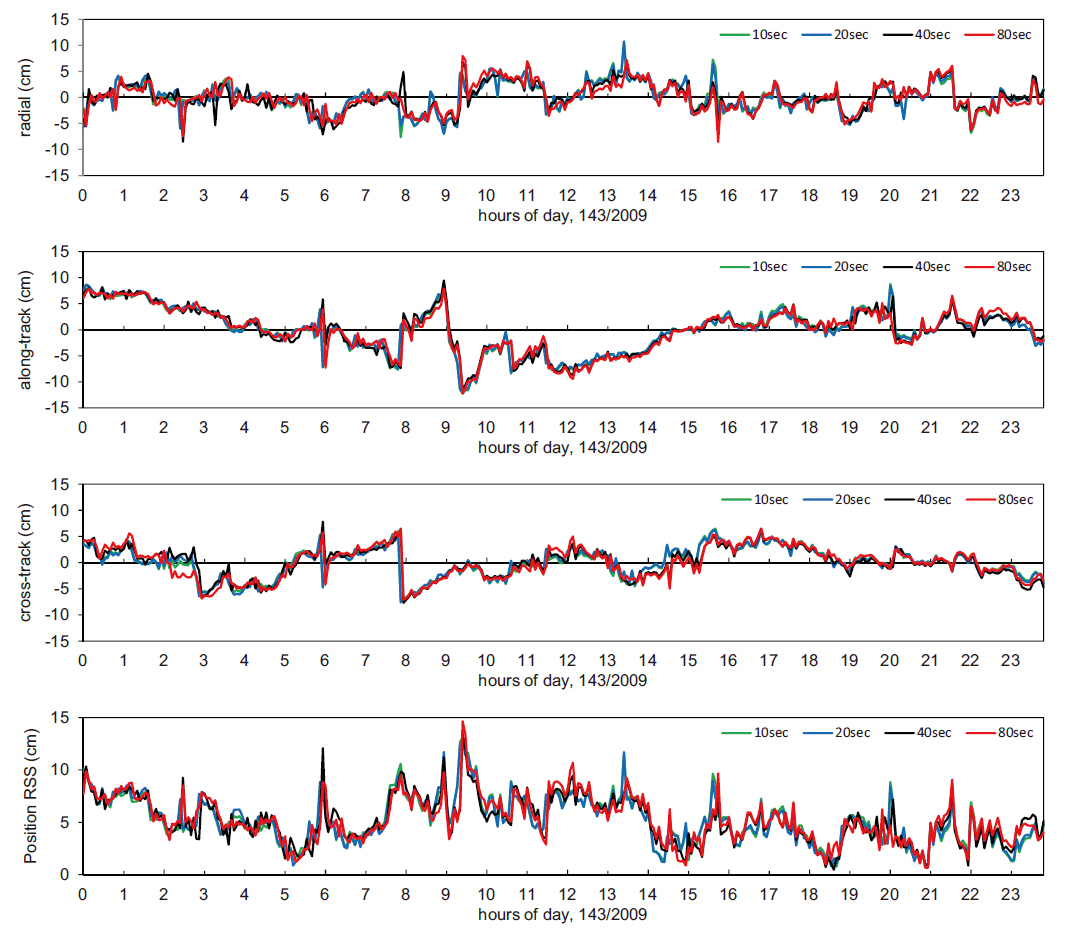
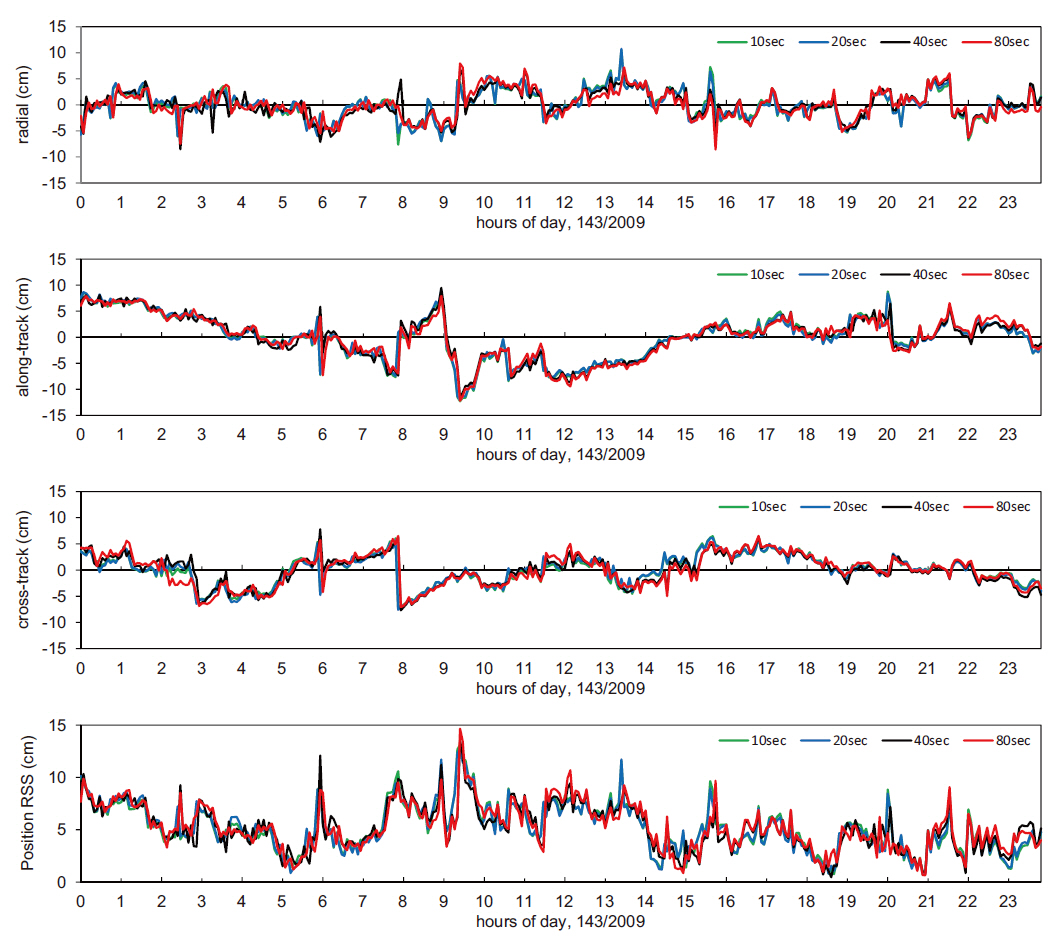
Figs. 4 and 5 show the radial, along-track, cross-track and three-dimensional positions obtained by the reduced-dynamic method and the kinematic method using the sampling measurement data in the 10, 20, 40 and 80 seconds of sampling intervals from the 24-hour observation data on the day of May 23, 2009, and their residuals in comparison with the JPL precise orbit ephemeris, indicating that the changing patterns were the same over time. In addition, Table 3 indicates that there was almost no difference in the precision among the sampling intervals.
In the geodesic field, the PPP of centimeter precision that is a single positioning method using the precise orbit ephemeris, the high-precision satellite clock correction terms, and dual frequency GPS receiver was suggested as an alternative of DGPS that is highly precise. PPP can be used for NRT applications if highly precise clock correction data is provided from IGS or self-estimated. If the LEO POD is performed by PPP, the precision similar to that of DGPS can be obtained in a simple way and the NRT processing requirement in the meteorological forecast can be satisfied. Since a high-precision dual frequency GPS receiver, IGOR, is loaded on KOMPSAT-5 to
obtain the GPS radio occultation measurements while satisfying the satellite position precision required for high-precision synthetic radar image processing, the PPP method that allows high-precision NRT POD is effective to utilize the atmospheric meteorological observation information in weather forecast.
In this study, we obtained 3 to 5 centimeters of precision in the single positioning POD in the reduced-dynamic method and kinematic method using the actual GPS data of the GRACE satellite on which the Blackjack receiver, the previous IGOR product, was loaded. In addition, we assessed the precision by varying the GPS measurement sampling interval from 10 seconds to 100 seconds and found that the orbit determination latency could be reduced by about one fourth without the position precision loss. POD with the measurements data having a longer sampling interval will be possible by adjusting the faulty measurement detection/correction parameter in the measurements pre-processing step so that the number of faulty measurements can be reduced and the number of valid measurements can be increased.