As data traffic demands increase rapidly, optical communication systems are widely used, providing high data rates with a large number of channels per fiber. However, optical fiber communication systems suffer from various linear and nonlinear transmission impairments [1]. Chromatic dispersion(CD) and polarization mode dispersion (PMD) are two important factors degrading the performance of high speed optical fiber transmission systems [2]. Intersymbol interference(ISI) caused by CD, PMD, and other impairments increases bit error rate (BER). As the transmission rate increases, ISI mitigation becomes indispensable and many schemes for CD and PMD compensation have been proposed. These compensation techniques can be separated into two approaches;optical domain equalization [3] and electrical domain equalization[2, 4, 5]. Optical equalization schemes can achieve perfect compensation using inverse system response, while the performance of electrical domain equalization is limited due to the nonlinear channel effect caused by the photodetector,which is a square-law detector. Nonetheless, electrical domain equalization schemes are widely used thanks to the multiple advantages, including compactness, flexibility, and low cost, that are brought by high-speed integrated-circuits technology.

Until now, most work on electronic domain equalizers has been focused on experimental studies [2, 5, 6]. The equalizer coefficients are determined by adaptive algorithms such as least mean square (LMS) algorithms and recursive least square (RLS) algorithms [7]. The obtained minimum mean square error (MMSE) solutions for optical on-off-keyed(OOK) systems have not been confirmed by theoretical studies.In this paper, we present theoretical closed form expressions for the MMSE linear equalizer coefficients and their MMSE performance. Through simulation, we verified that the calculated equalizer coefficients coincide with estimated equalizer coefficients using adaptive algorithm. Furthermore, once the MMSE equalizer coefficients are obtained, it is possible to estimate MSE performance of the MMSE linear equalizers in square-law nonlinear channels.

The rest of the paper is organized as follows. The next section describes the system model and computation of MMSE linear equalizer in square-law nonlinear channels.Simulation results using optical communication system are discussed in Section III. Section IV concludes the paper.

Consider a typical non-return-to-zero on-off-keyed (NRZ-OOK)optical communication model in Figure 1.

The bit sequence {b_k} with a bit rate T is pulse shaped by a continuous time pulse p(t) (for example, a raised cosine pulse with roll-off factor 1),

and transmitted over an optical fiber after laser modulation.We assume the fiber is a lossless linear channel with CD and first order PMD distortion. The CD and PMD are generally non-linear distortions, but often modeled as a linear distortion by a first order approximation in the optical field domain.The effect of dispersion can be modeled as a linear filtering process given by

where S_o(t), r_o(t), and h_o(t) are the transmitted, received signals, and the fiber impulse response in optical field domain,respectively, and ？ denotes convolution.

For example, the first-order PMD including CD distortion can be characterized as the following frequency response [2]

where L denotes the fiber length, λ the wavelength, D the dispersion parameter at λ, and c speed of light, γ the power splitting ratio, telling how the power of the input light of the fiber is divided onto the two input principle state of polarization, and τ denotes the differential group delay between the two polarizations.

The received optical signals having undergone these dispersions are demodulated to electronic signal by a squarelaw detector. In contrast to the signal detection process in wireless communication systems, this process is nonlinear.Hence, the linear convolution relation in optical field domain is not preserved in the baseband electronic domain.The received signal in electronic domain is

where w_o(t) denotes noise in the optical domain due to fiber amplifier and w_e(t) denotes the noise in the electronic domain. In the discrete time domain, by denoting r_k:=r_e(kT)with ideal sampling timing phase [8],

where c_o(t) denotes the combined impulse response with the pulse shaping filter p(t) and PMD/CD h_o(t). We assume that the amplified-spontaneous-emission (ASE) noise from the erbium-doped fiber amplifiers dominates and the electronic domain noise can be neglected, i.e w_e(t)=0. Then, the whole process can be modeled as a linear channel followed by a square law detector as illustrated in Figure 2.

We assume that the transmitted signal x_k consists of {0, σ_x}to model OOK (σ_x=1 for the conventional OOK), and discrete time channel model c = [c₀,…c_Nc-1]^T represent the optical domain channel, where [·]^T denotes transpose operator.Furthermore, w_k denotes the zero-mean optical noise with variance σ²_nand y_k denotes the output of square law detector. It is assumed that the transmitted signal x_k and noise w_k are statistically independent. In the next section we will derive MMSE equalizer applied to y_k under this channel mode.

In contrast to the case in conventional wireless communication systems, the source signal x_k in our channel model has nonzero mean and the following properties which make the derivation of MMSE equalizer difficult:

where E[·] denotes the expectation.

Denoting xk = [x_k,…x_k-(Nc-1)]^T a vector consisted of the source signals, the optical received signal before square law detector is expressed as

And the input to the linear equalizer is given by

Let f = [f₀, …f_Nt-1]^T be the linear equalizer of length N_f.The MMSE equalizer coefficients of f is obtained by minimizing MMSE cost function

where y_k = [y_k, …, y_k-(Nk-1)]^T and Δ is decision delay. It is well known that the MMSE solution of f is given by the following [7]

The goal of this paper is to express E[y_k y_k^T] and E[y_Δ y_k]in terms of the channel c = [c₀,…, c_Nc-1]^T, the signal magnitude σ_x, and the noise variance σ²_x. In order to obtain E[y_k y_k^T]^-1, we need to calculate E[y_k y_k^T] as shown below.

We know that E[y_ky_k]= E[y_k-δy_k-δ] = E[y_k-δy_k]. Because E[y_ky_k^T] is symmetric Toeplitz matrix [7], we have only to compute one row or column of E[y_ky_k^T]. Note that E[y_ky_k^T]^-1 is also a symmetric matrix. The elements of E[y_ky_k^T], E[y_ky_m], are very complicated to compute since the transmitted signal x_k has nonzero mean and the equalizer input y_k is the magnitude square of received signal r_k. Hence, it is impossible to provide a simple linear solution in contrast to the linear channel case. E[y_ky_m] is composed of the following four terms:

Let’s define the first term of E[yk ym],

as a function α(k, m, c, σ²_x, σ²_n) :

When k = m

When ' k ?m '=δ (≠ 0)

The second term is a product of two expectations

where 1=[1,…,1]^T is the vector of length N_c consisting of 1’s. Note that

The third term, the noise term, can be expressed as the square of noise variance.

The last term becomes the second term, when k = m.

Now, we have obtained the element of E[y_ky_k^T],

Consequently, we have obtained E[y_ky_k^T] in terms of the channel c = [c₀,…,c_nc-1]^T, the signal magnitude σ_x and the noise variance σ²_x as desired and consequently E[y_ky_k^T]^-1 can be computed by matrix inversion. Finally, we can obtain the MMSE equalizer tap f by computing E[y_Δ y_k]as shown below.

Once equalizer tap coefficients are obtained, the MSE performance of the linear equalizer can be calculated by substituting equalizer tap f into the MMSE cost function.

Once optical channel, optical noise variance, and the signal magnitude are given one can determine the MMSE equalizer and its MMSE performance. Numerical program languages such as Matlab are quite helpful to utilize the above results.

We consider mainly CD distortion to demonstrate the analysis on the electronic MMSE linear equalizers for optical OOK. In the frequency domain, the optical channel is given as

where the fiber CD parameter D is set to 17ps/nm/km, L is the fiber length, c is the speed of light, and λ is the signal wavelength, which is assumed to be 1550nm. By taking the inverse Fourier transform, the time domain transfer function can be calculated and expressed as [9]

In order to produce a discrete time channel impulse response, continuous time transfer function is sampled at a rate of 1/T where T is the symbol period.

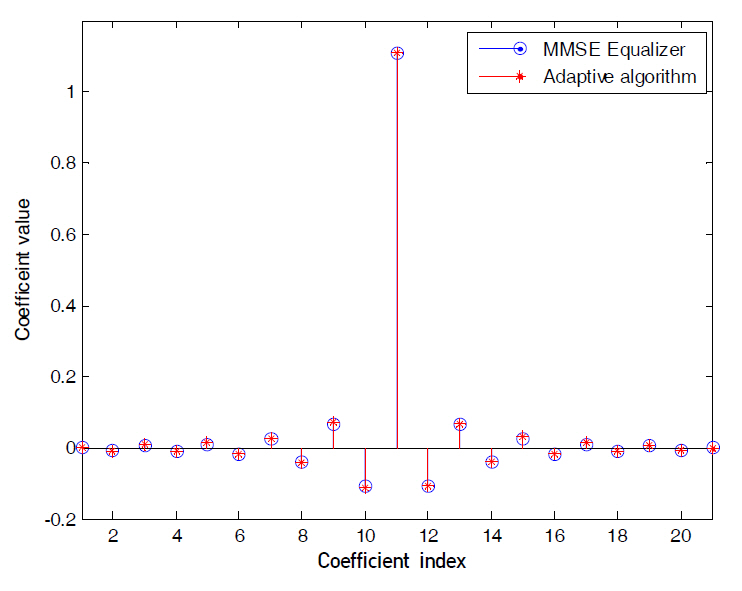
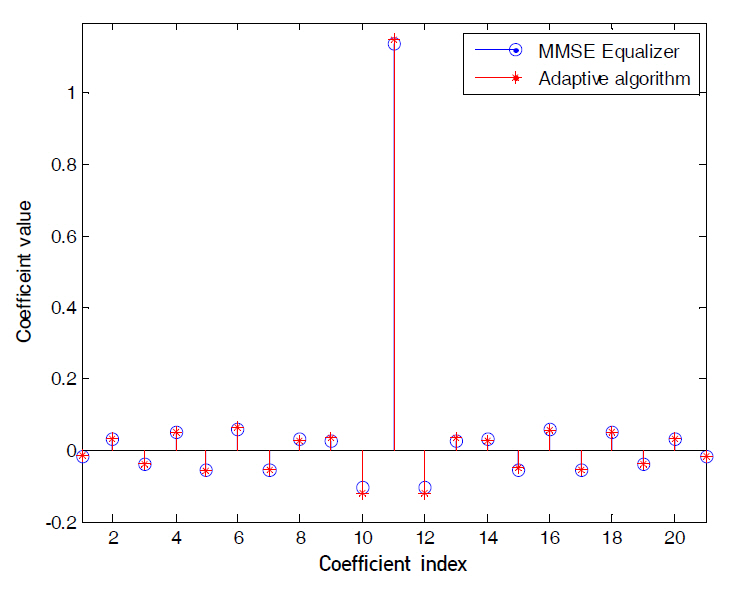
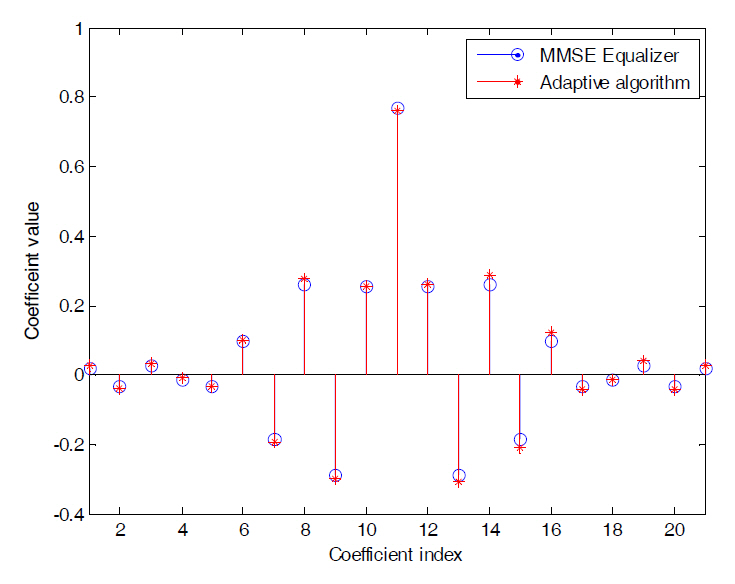
Fig. 3~5 compare the MMSE equalizer coefficients of N_f = 21 computed from analytical method and computed by adaptive algorithm for various degree of CD controlled by fiber length. The x- axis denotes the equalizer coefficient index k=1,…,21 and the y- axis draws the corresponding coefficient value f_k. The agreement of two equalizer coefficients indicates the validity of the previous analysis that the computed linear equalizer is MMSE equalizer in squarelaw nonlinear channels.

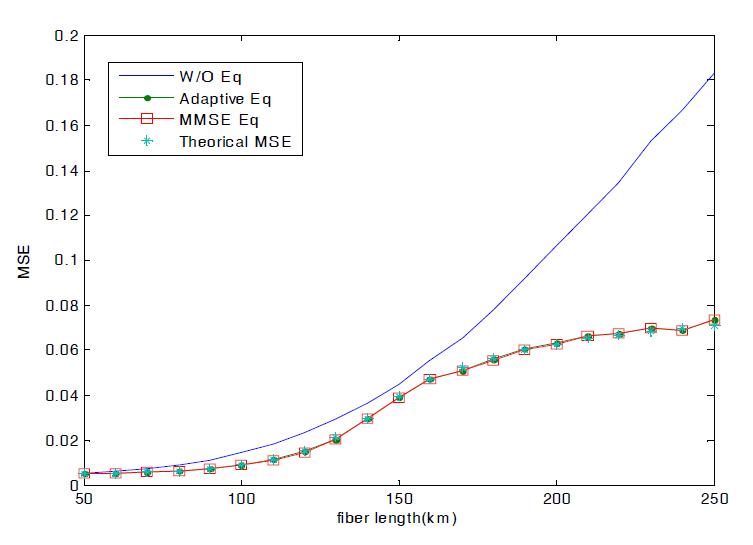
Fig. 6 shows that the MSE performances of two equalizers also agree. This result suggests that the MMSE performance of a linear equalizer for CD can be analytically computed instead of adaptive simulation.

We have performed analysis on the MMSE linear equalizer in square-law nonlinear channels found in optical OOK system and presented the MSE performance of equalizer. It has been verified that the analytically driven equalizer is indeed the MMSE solution by comparing with simulated equalizers by adaptive algorithms. As a result,we are able to theoretically bound MMSE performance of the electronic domain linear equalizer applied to optical OOK systems.